内部爆炸薄圆板的变形及有效载荷*

2020-11-27李芝绒张玉磊袁建飞王胜强

爆炸与冲击 2020年11期

李芝绒，张玉磊，袁建飞，王胜强

（西安近代化学研究所，陕西西安 710065）

内爆炸毁伤是打击水面舰船重要的毁伤方式，战斗部内爆炸产生的压力载荷作用于舰船舱壁结构，产生侧舷、横舱壁等结构变形或破坏，导致船舱进水，严重时可造成整船沉没。由于内爆炸载荷是一种多波峰叠加的复杂压力波，瞬态压力峰值高，载荷作用时间长，对船体结构的毁伤破坏比自由环境下的爆炸毁伤更剧烈、更复杂，因此，内爆炸载荷作用下结构的失效破坏成为了国内外学者研究的热点。

对于爆炸载荷作用下板结构的变形失效，已开展了大量的实验研究和理论分析。Nurick 等[1]、Wen[2]开展了周边固支低碳钢圆板受均匀载荷作用的变形实验研究。Jacob 等[3]、Gupta 等[4]开展了固支圆板在空爆载荷作用下的边界撕裂破坏实验研究。Geretto 等[5]开展了均布载荷作用下固支方板的失效模式实验。Teeling-Smith 等[6]利用有限元分析软件开展了均布脉冲载荷作用下软钢薄圆板的变形撕裂研究，得到了板厚度、不同边界支撑等特性对板变形的影响。朱锡等[7]、陈长海等[8]开展了爆炸载荷作用下固支方板的变形实验研究。崔高领等[9]进行了均布冲击载荷对金属方板的仿真计算研究。这些研究均在空爆或半密闭环境下开展，而对于密闭环境下板结构变形与载荷关系的研究较少，如姚熊亮等[10]开展的舰船舱内爆炸载荷特征与板架毁伤规律仿真研究，侯海量等[11]开展的舱内爆炸载荷及舱室板架结构的失效模式研究。与空爆压力载荷相比，密闭环境下的压力载荷是一种多波峰叠加、准静态压力作用时间长的复杂压力波，受压后的板结构在产生塑性变形的过程中还存在极限变形[12]现象，即结构变形达到一定值后不会持续增大，后续阶段的压力载荷对结构变形不产生影响。这种产生板结构极限变形的压力载荷称为有效压力载荷或饱和压力载荷，研究有效压力载荷随时间的变化规律，掌握其与板结构的耦合作用关系，成为研究内爆炸结构变形破坏的关键。郑成等[13]、孔祥韶等[14]通过仿真计算方法，研究了密闭方形结构内方薄板的变形特性，并提出了方板变形预报模型和内爆炸压力载荷等效模型。而通过内爆炸实验方法研究板结构的变形特征与压力载荷关系，目前鲜有报道。

本文中基于双圆筒爆炸装置，开展TNT 和某温压装药对铝质、钢质薄圆板的内爆炸实验，获取薄圆板的变形和压力载荷数据，分析薄圆板的破坏模式和压力载荷特点，并基于相同变形下作用载荷相等原理，确定薄圆板极限变形的有效比冲量和作用时间，提出圆薄板变形的预报模型并进行验证，以期为内爆炸结构毁伤研究提供技术参考。

1 实验方法

1.1 实验装置及样品

实验双圆筒装置如图1 所示，由两段圆筒、薄平板、前/后端盖、密封圈组成，在圆筒端部设有法兰盘。薄平板放置于两个圆筒端部的法兰盘之间，由螺钉将两个圆筒、薄平板密封连接，形成两个密闭圆筒腔室。圆筒长1 670 mm，内径800 mm，壁厚12 mm。为达到薄平板与法兰盘连接接近固支条件，在法兰盘的端面上铣出几组细浅同心圆，并对圆筒内端面角作倒圆角处理，减小其对薄板变形的影响。薄平板为2 mm 厚的铝板和1 mm 厚的Q235 钢板，在靠近边缘的同心圆周上，设置与圆筒法兰盘孔对应的圆孔。实验装药为柱形TNT 和某温压装药，长径比1∶1，其中TNT 密度为1.58 g/cm3，质量分别为20 和40 g；某温压装药（主要组成为HMX 和Al 粉）密度为1.84 g/cm3，质量分别为20、30、40、50、60、70 和80 g。实验时，将药柱垂直悬挂于圆筒的几何中心，由电雷管起爆1 g C4 扩爆药柱，引爆装药。

图1 双圆筒爆炸装置及测点布设位置Fig. 1 Double cylinder explosive device and locations of measuring points

1.2 测点布局及测试系统

在爆炸圆筒一端圆形盖板的中心轴线上，按照从圆心到边缘的顺序均布4 个压力测量点P1、P2、P3、P4，如图1(c)所示。测点布设的压力传感器为PCB 公司113B24 型壁面压力传感器，量程为0～6.9 MPa。传感器敏感面距盖板内表面约0.8 mm。安装完成后，在传感器头部敏感面与安装孔形成的凹槽内涂满油脂，使油脂表面与盖板表面平齐，其目的是延长爆炸热传递到传感器敏感面的时间，减小热冲击对压力载荷测量的影响。

基于爆心对称的两个刚性壁面上，冲击波在静止刚性壁面的反射压力与运动刚性壁面的反射压力差异不大[15]，可近似认为实验获取的盖板测点压力载荷等于圆薄板对称位置的压力载荷。

2 实验结果及分析

2.1 圆板变形结果及分析

本文中共进行了10 个工况实验，其中工况1～3 为铝质薄圆板的变形破坏实验，工况4 是为了补充获取工况2 开展的40 g TNT 装药在爆炸室的压力载荷数据实验，工况5～10 为钢质薄圆板的变形破坏实验。典型铝质、钢质薄圆板实验后的状态如图2 所示，各实验工况薄圆板的变形挠度及破坏情况如表1所示，其中WY 代表某温压装药。

图2 典型铝质、钢质薄板实验后状态Fig. 2 Pictures of typical aluminum and steel thin circular plates after experiments

表1 各实验工况圆板的变形结果Table 1 Deformation results of circular plate under various experimental conditions

由图2 可以看出，工况2 的铝质薄圆板从夹持边界剪切断裂，切下圆板飞向邻室，落于后端盖底部，扭缩成团，如图2(b)所示，其剪切断面边缘有微小弯曲和大小不均匀的小尖刺。除工况2 外，其他工况的铝质、钢质薄板均产生了四周顶起的锥形隆起结构，在薄板的夹持边界和中心区域产生了显著塑性大变形，在中心区域形成了比周边结构更陡峭的锥尖，且锥角随装药质量的增大而减小，更尖锐。在工况3的铝板夹持边界还产生了两段不连续的断裂裂缝，如图2(c)中红色圈内标注线及左侧放大图所示，从裂缝断面可以看出，夹持边界有显著的板厚拉伸减薄现象，断面边缘不规则，有长度不等的细长尖刺。工况5～10 的装药为某温压药，钢质薄板产生了大变形，变形挠度随装药质量的增加而增大。

从上述圆板变形结果可以看出，在圆板夹持边界和中心产生了塑性大变形，在夹持边界还出现了局部撕裂和剪切断裂现象，主要原因是在圆板夹持边界和中心产生了应力极值点。参考方形薄板的应力响应分析[16]，在爆炸压力载荷作用下，固支夹持边界处形成弯曲转角，产生拉伸应变，当弯曲应变小于边界极限应变时，夹持边界产生大弯角，形成的运动塑性铰环从夹持边界向圆板中心移动收缩。在塑性铰环内部，圆板作刚体平行移动[17]，塑性铰环通过的外部则形成了曲面板，并按照锥形分布速度运动。当后续压力载荷作用下，圆板变形不持续增大时，塑性铰环收缩到圆板中心，形成锥尖；当弯曲应变接近板的极限应变时，在夹持边界产生局部的撕裂；当超过板的极限应变后，夹持边界产生横向剪切断裂。

圆板的实验结果表明，在内爆炸载荷作用下，薄圆板产生了3 种破坏模式：塑性大变形、拉伸撕裂、横向剪切。该结果与文献[14]所得到的空爆压力载荷作用下梁、圆板的变形破坏模式一致。

2.2 圆板上的压力载荷及分析

工况7 的4 个测点测量的压力载荷曲线和积分处理后的比冲量曲线如图3 所示。从图3(a)的压力载荷曲线可以看出，4 个压力测点的压力载荷到达时间差小于0.12 μs，P1、P2、P3 测点最大压力峰值基本一致，角隅测点P4 的最大峰值约为其他测点最大峰值的2 倍，4 个测点的压力载荷随时间的变化趋势基本一致。从图3(b)的比冲量曲线可以看出：在3 ms 内，4 个测点的比冲量大小与比冲量增长量基本一致，虽然P4 测点的最大压力峰值最高，但是比冲量与其他测点基本相当；3 ms 后，除P3 测点外，其他测点的比冲量增长量基本一致。观察P3 测点的压力载荷曲线发现，3 ms 后，其压力值比其他测点略小，原因可能是受到爆炸热冲击对压力传感器性能的影响，由于压电型传感器具有热释电效应，当传感器的隔热防护作用不够时，爆炸热通过热传导作用到传感器的敏感元件上，输出热冲击干扰信号，并且传感器的预紧结构受热膨胀，预紧力减小，导致传感器的灵敏度变小，输出的压电信号也减小。

图3 工况7 的4 个测点压力载荷曲线和比冲量曲线Fig. 3 Pressure load curves and specific impulse curves of four measuring points under condition 7

其他实验工况下4 个测点的载荷特性与工况7 基本类似，除角隅位置压力载荷的最大峰值是其他测点的2 倍外，其他时刻4 个测点的压力载荷大致相等，比冲量也基本一致。因此可由一个测点的压力载荷反映整个圆板面上的压力载荷。各工况圆板中心测点P1 的压力载荷曲线如图4 所示。

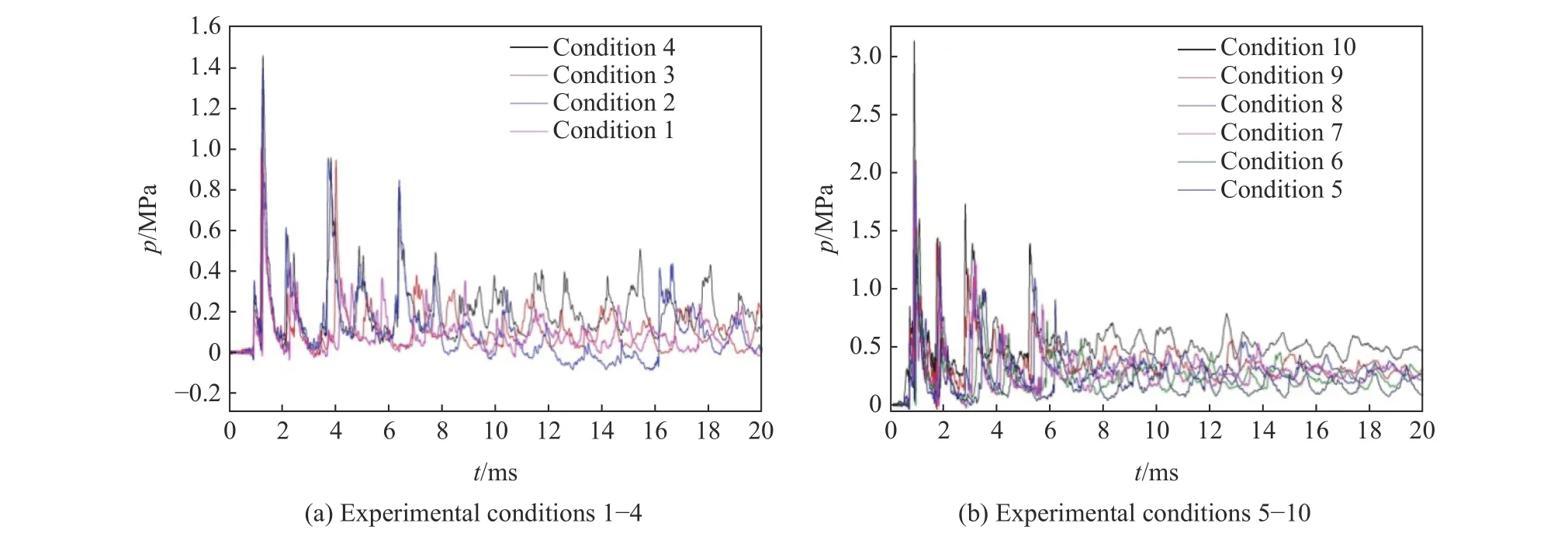
图4 各实验工况圆板中心的压力载荷曲线Fig. 4 Pressure load curves of circular plates under various experimental conditions

从图4 所示的压力载荷曲线可以看出，薄圆板受到多波峰叠加的复杂压力载荷作用。在初始阶段，压力波以显著的一大一小波峰组合周期性衰减出现，变化周期为2.8～3.5 ms（药量越大周期越短），每一周期内的波峰值均比前一周期对应的波峰值小，3 个周期后，两个波峰逐渐融合，形成了压力波动逐渐减小的准静态压力。工况2 的压力曲线在7.9 ms 内，波形特征与其他工况的变化规律类似，7.9 ms后压力逐渐减小，形成约12 ms 的周期性振荡波。工况5～10 的压力载荷最大峰值和匀化形成的准静态压力均随着装药质量的增大而增大，但振荡周期随着装药质量的增大而缩短，从3.5 ms 逐渐缩短到2.8 ms。

将上述各工况圆板中心测点P1 的压力载荷积分处理，得到比冲量时间曲线，如图5 所示。

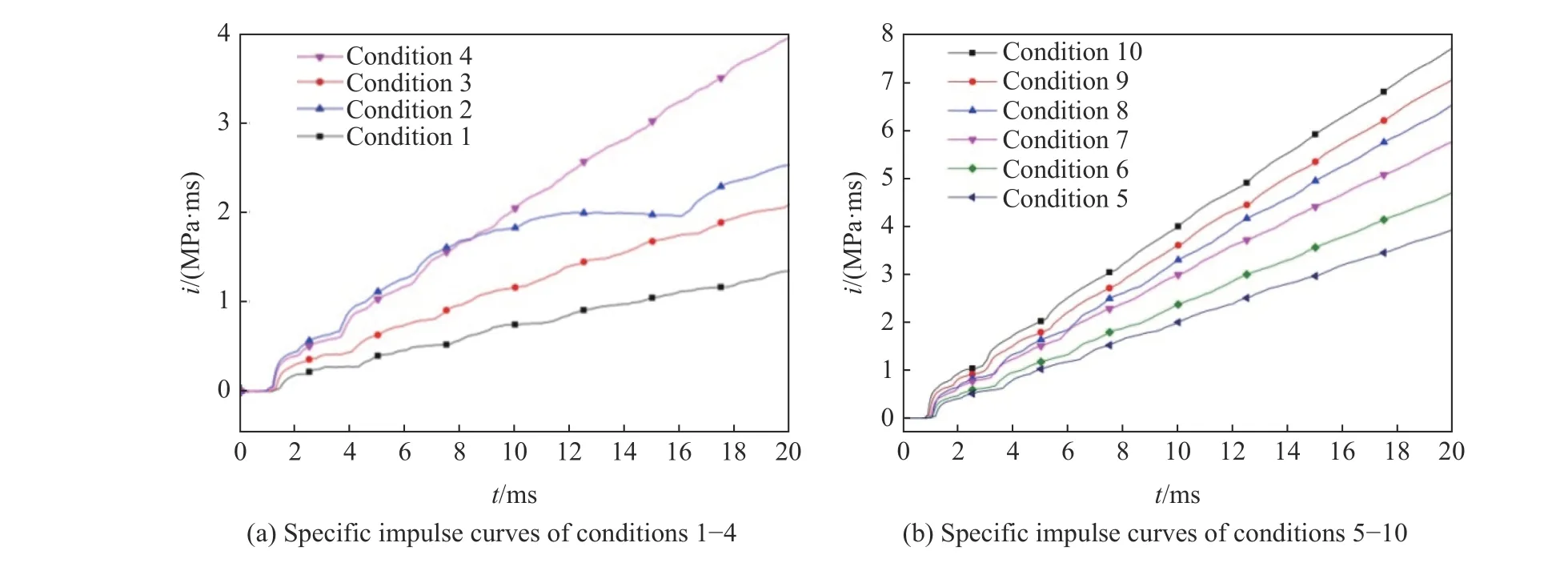
图5 各实验工况圆板中心比冲量曲线Fig. 5 Specific impulse curves of circular plates under various experimental conditions

除工况2 外，其他工况的比冲量时间曲线变化规律类似，在约0.35 ms 内，比冲量曲线急剧上升，随后呈波浪式增长，并且随着时间的延长，波浪振幅逐渐减小，逐渐趋于线性增长。这主要是由于爆炸室内压力波趋于匀化，形成了压力波动较小的准静态压力所致。比冲量波动周期等于压力载荷波动周期，并且随着装药质量的增加，比冲量也随之增大。

工况2 与工况4 的装药类型和装药质量相等，比冲量值在7.9 ms 内基本一致，7.9 ms 后，工况2 的比冲量增长率相对减缓，形成了周期约12 ms 的新波动。结合工况2 薄圆板的破坏结果，可得到在7.9 ms时刻，铝板受到的比冲量为1.720 MPa·ms，铝板夹持边界的弯曲应变超过板的极限应变，产生了瞬时剪切断裂现象。工况3 的铝板夹持边界产生了两小段撕裂破坏，其破坏时刻的弯曲应变接近铝板的极限应变，受到的比冲量应小于1.720 MPa·ms。工况5～10 的钢质薄圆板，在压力载荷作用时间内，夹持边界产生的弯曲应变均小于材料的极限应变。

基于圆板上比冲量时间曲线呈线性增长的特点，其增长量由圆筒内形成的准静态压力产生，因此，除去比冲量曲线前期0.35 ms 内的急剧上升段，选取0.35～20.0 ms 的比冲量数据作线性拟合处理，得到比冲量平均增长率，该增长率近似等于圆筒内的准静态压力。由于急剧上升段的比冲量主要由压力载荷的最大峰值脉冲积分产生，脉冲持续时间短，可以近似认为圆板受到的比冲量瞬时增长到 Δi，然后线性增长，因此，圆板上的比冲量i可表示为：

式中：p为圆筒内准静态压力，t为压力载荷作用时间， Δi为比冲量快速增长量。

对各工况的比冲量数据进行处理，可得到各工况的准静态压力p和比冲量快速增长量 Δi。表2 为工况5～10 的准静态压力p和 Δi以及3、5 和10 ms 时的比冲量实验值和依据式(1)得到的计算值。

表2 工况5～10 的 p 和Δi 及典型时刻模型比冲量的计算值和实验值Table 2 p and Δi of conditions 5-10 and the calculated and experimental specific impulses at typical times

对比表2 中的比冲量计算结果和实验结果可知，3、5 和10 ms 时段内的计算结果与实验结果的偏差分别为13.6%、8.3%和4.5%。可以看出：随着载荷作用时间的加长，模型计算结果与实验结果的偏差减小。这表明比冲量计算模型可以近似预估圆板受到的比冲量，且载荷作用时间越长，计算结果越接近实验结果。

Barker 等[18]提出了一种内爆炸准静态压力p计算模型：

式中：m为炸药装药质量，V为内爆炸空间体积，A、 γ 为相关因子。

将上述工况5～10 的准静态压力p的实验结果、实验装药、圆筒体积，按照式(2)的幂指数模型进行拟合，可以得到该装药的准静态压力计算模型，其中：系数A=1.865，γ =0.67。依据该计算模型得到工况5～10 的准静态压力p为0.200、0.243、0.282、0.319、0.353、0.386 MPa，与表2 中压力的实验结果进行比对可知，偏差小于4.7%。

上述快速增长比冲量 Δi，主要由压力载荷曲线中起始段最大峰值的压力脉冲积分得到，该脉冲的最大峰值、脉宽与装药质量及爆心距相关，因此，按照比冲量与比对距离成幂指数关系：

式中：K、δ 为因数，r为内爆炸爆心距。将表2 中工况5～10 的 Δi实验值、装药质量、爆心距按照式（3）的幂指数模型进行拟合处理，得到K=2.051，δ=2.11。依据该模型计算工况5～10 的 Δi分别为0.299、0.372、0.441、0.506、0.569、0.630 MPa·ms，与表2 中 Δi的实验结果比对可知，偏差小于3.3%，表明该模型能够描述冲量曲线中快速增长段的比冲量 Δi。

将式(2)、式(3)代入式(1)，则式(1)转化为：

2.3 钢质圆板变形的有效载荷分析

Zhao 等[12]提出了平板变形的极限响应现象，即在平板变形达到一定值后不会持续增加，后续的作用载荷对平板的变形不产生影响，存在平板极限变形的有效载荷及作用时间。对于薄板结构，一般遵循冲量毁伤准则，即对薄板的破坏主要由冲量载荷产生。在空爆环境下，冲量值可通过冲击波压力正压时间内的比冲量与板面积的乘积得到，而在内爆炸环境下，由于压力载荷为多波峰叠加并逐渐匀化为准静态压力的复杂波，正压时间长，无法确定载荷作用时间，因此不能依据获取的压力载荷数据直接得到有效比冲量和作用时间。

上述内爆炸压力载荷未完全匀化前的压力波，可近似看作一种瞬态升压后又缓慢衰减的单波峰压力波（忽略内部压力波动），与外爆炸压力波波形特点相似。因此，可基于相同变形下冲量载荷相等原理，认为空爆条件下圆板受到的冲量载荷等于内爆炸条件下圆板极限变形所受到的有效冲量，再依据有效冲量，得到载荷作用时间。

在空爆条件下，Jacob 等[19]提出了钢质圆板的变形挠度计算模型：