颗粒多孔介质中油水两相流动特性数值模拟研究*
2020-11-26黄志江吕孝飞赵会军宋琳琳杨草来张建龙
黄志江 吕孝飞 赵会军 宋琳琳 杨草来 张建龙
(常州大学石油工程学院,江苏省油气储运技术重点实验室 江苏常州 213164)
0 引言
油品在土壤、砂砾等多孔介质中的流动阻力特性研究在实际工程应用中具有重要意义,如研究埋地油品管道泄漏后的迁移扩散规律、清除泄漏后的油污区域等问题时,油品流经土壤、砂砾时的阻力压降是进行相关研究的重要参数[1-2]。目前,国内外学者借助实验和数值模拟方法,对多孔介质中的流体流动阻力特性进行了研究并有了一定的认识。PASCAL J P等[3]研究表明,当流体以低雷诺数流动时,压力梯度主要用于克服黏性阻力,当流速增大到一定限度,惯性阻力的影响增大,压力梯度需同时克服黏性阻力和惯性阻力;JAN H[4]研究了单相水在各种均匀分级颗粒多孔介质中的流动行为,发现多孔介质中孔隙结构的几何形状对流动阻力影响很大;SYLWIA R[5]发现聚合物溶液通过多孔介质时,会受到剪切和拉伸致使流动阻力大幅增加;张震等[6]对多孔介质内单相流的绝热流动阻力进行了数值模拟,分析了惯性损失系数对流动阻力的影响;刘学强等[7]对紊流流态区间下多孔介质中单相流的阻力特性进行了实验研究,得出相应的数学模型;李振鹏等[8]采用玻璃球填充的多孔介质通道对单相水的流动阻力特性进行实验研究,得出相应阻力压降计算公式;于立章等[9-10]应用相似理论,合理地缩减多孔介质通道的尺寸,建立了多孔介质通道中单相水绝热流动压降预测模型;吴国忠、齐晗兵等[11-12]测量了油水混合液在颗粒多孔介质通道内的流动阻力,拟合了其压降-速度表达式,并得到其黏性和惯性阻力系数;张淑淑等[13]研究了储罐内填充不同的多孔材料厚度下,液化天然气在储罐内的流动情况。以上这些研究结果使人们对多孔介质中单相流的流动规律有了比较深入的认识,但对两相流及多相流在颗粒多孔介质中的流动特性的认识较少。本文考虑到油水两相流比单相流的流动形态更为复杂,油水相比可能对阻力压降的影响显著,多孔介质中孔隙分布具有随机性,流经不同长度多孔介质通道时产生的阻力压降也应有较大差异,故对油水两相的相比和多孔介质通道长度进行对比分析,得到它们对流动阻力压降的影响程度,对实际工程应用有很好的指导意义。
本文构建小球颗粒填充多孔介质通道几何模型并结合CFD数值模拟计算,探讨不同油水比工况和不同多孔介质通道长度工况下,流动阻力压降随入口流速的变化规律,为输油管道泄漏污染物在多孔介质中的流动特性提供可靠的依据。
1 数值模拟
1.1 几何模型及网格划分
为保证多孔介质通道几何模型的可行性,采用参考文献[6]中的实验参数,即内径为0.05 m,管长为1 m的有机玻璃管内紧密填充直径8 mm的均匀粒径玻璃小球颗粒,其孔隙率为0.408。模型尺寸以实验所用多孔介质通道尺寸为依据,考虑到网格数量及网格质量的影响后,按照2.5∶1的比例绘制上述多孔介质通道简化的几何模型。为简化网格数量和减少计算量,根据圆管模型的对称性,可选取1/4圆管通道作为模拟流域,小球颗粒以四棱锥结构为基本单元进行填充,在近壁面间隙较大部分,使用不同体积的半球进行填充,如图1所示。
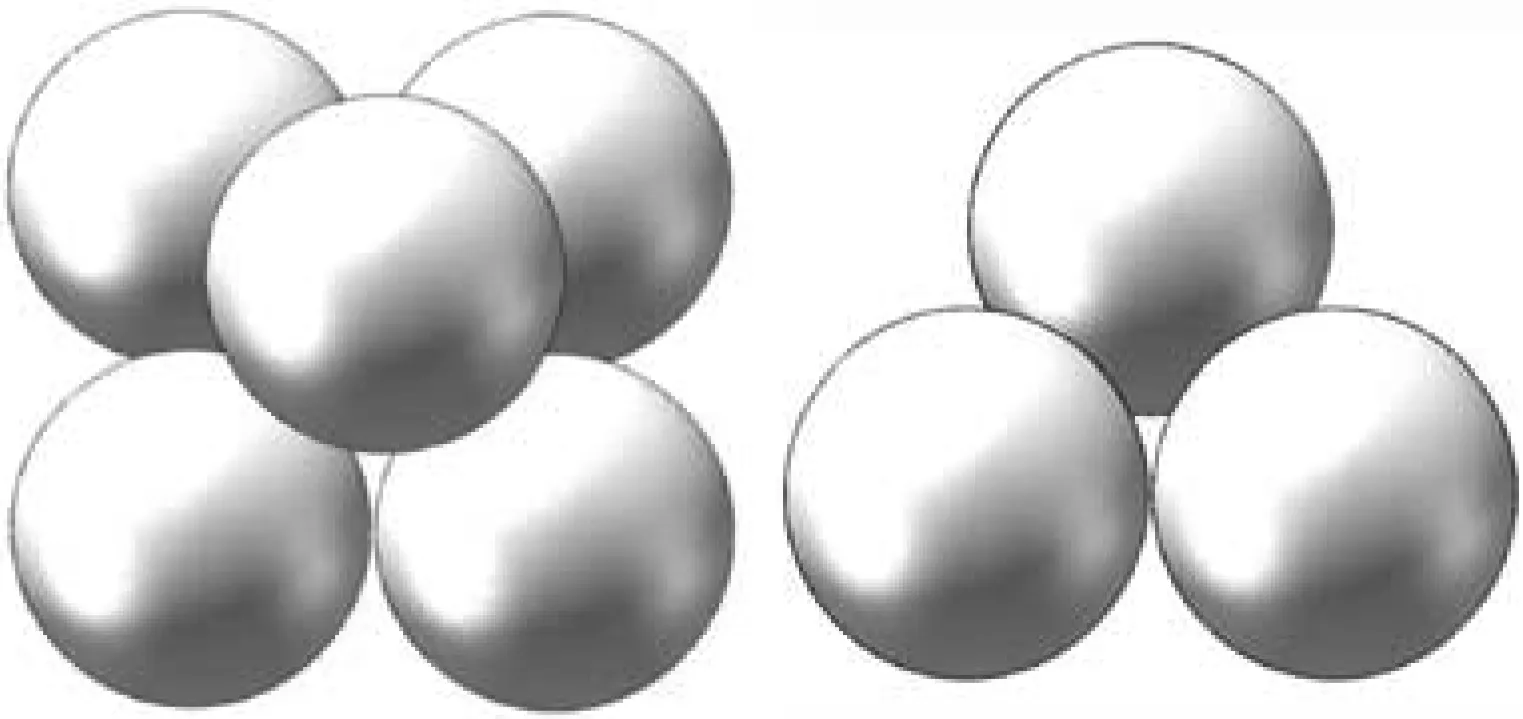
(a)俯视图(局部) (b)左视图(局部)
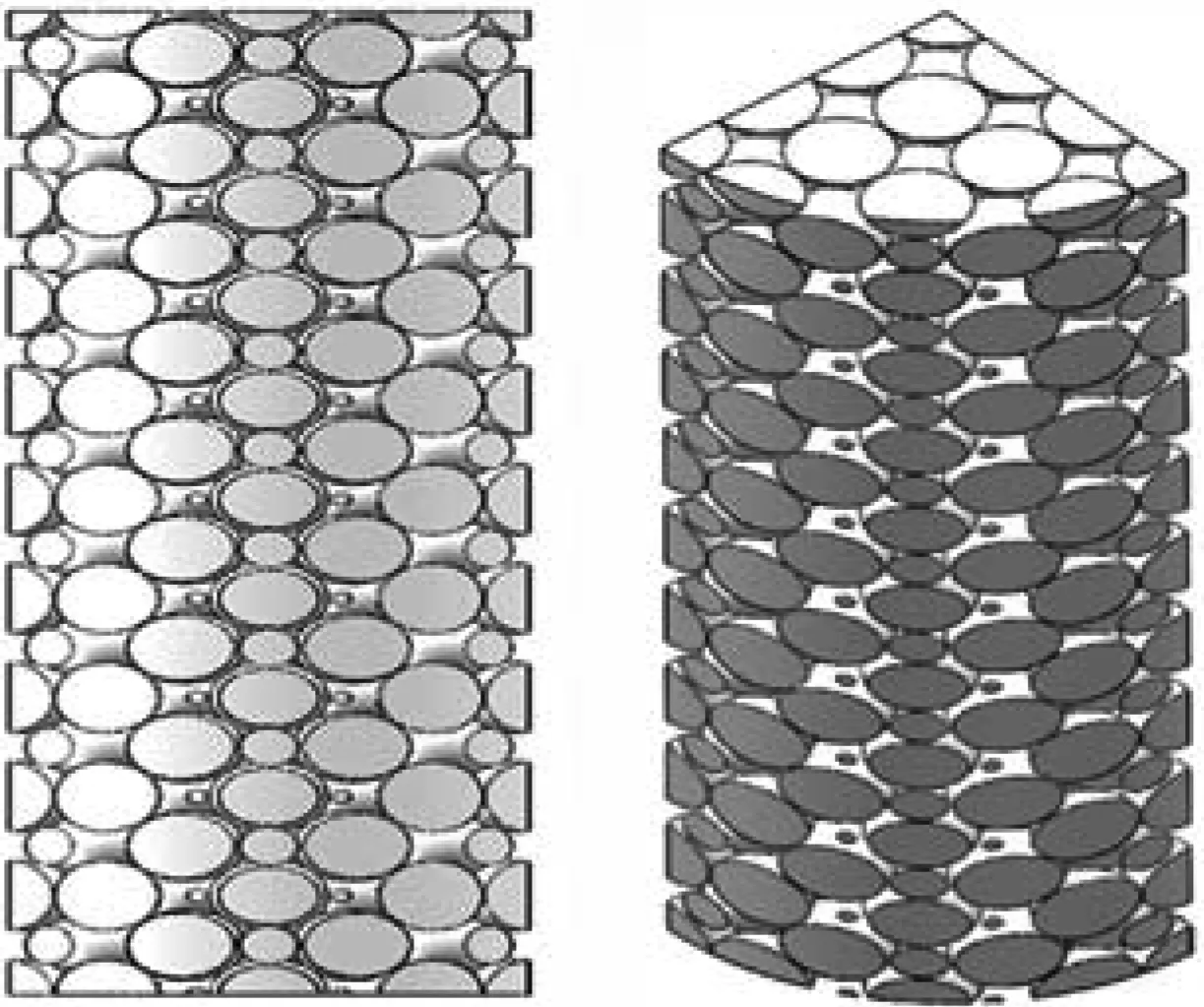
(c)主视图 (d)斜视图图1 多孔介质通道小球排列示意
在管道无障碍空间内作稳定流动的流体流入多孔介质通道时,会经过一个过渡段(过渡段长度l与管道内径d相等)才能成为速度均匀发展的稳定流动,如图2所示[14]。可以适当缩小几何模型中多孔介质通道稳定流动段长度来合理简化模型。根据以上分析,确定模型入口空管段长度为0.02 m,小球填充多孔介质段长度为0.045 m,出口空管段长度为0.02 m,如图3所示。
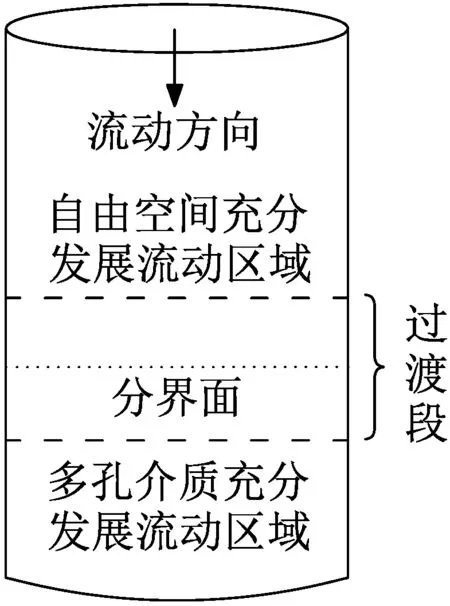
图2 流体流入多孔介质示意
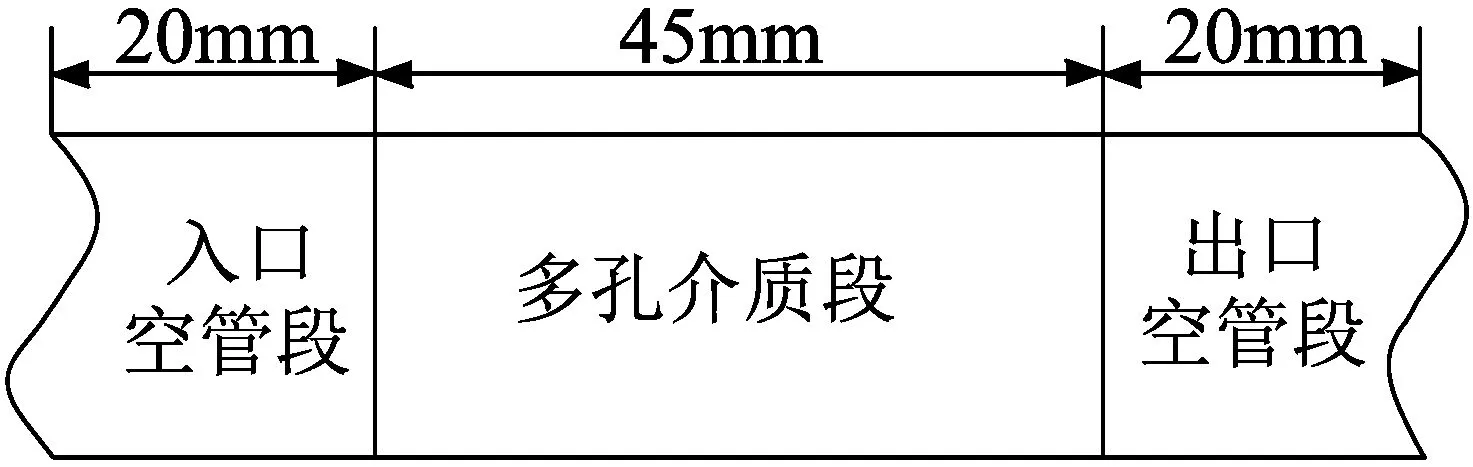
图3 流动通道示意
为了保证网格正常生成,在构建几何模型时,需使小球颗粒与小球颗粒之间留有微小的缝隙。因此,本文对径向的小球分布采取相互分离的排列方式,对轴向的每层小球采取镶嵌的排列方式。通过这种正负误差抵消的方法,可以降低整个通道内的误差[9]。
由于模型不规则程度高,不易生成计算量大的六面体网格,故选用非结构四面体网格进行划分,为保证计算结果的精确,对小球颗粒间的缝隙区域生成的网格进行加密处理,如图4所示。经网格无关验证,确定网格数为4 326 709个,其中95%的网格的偏斜度为0到0.25,网格质量满足计算要求。
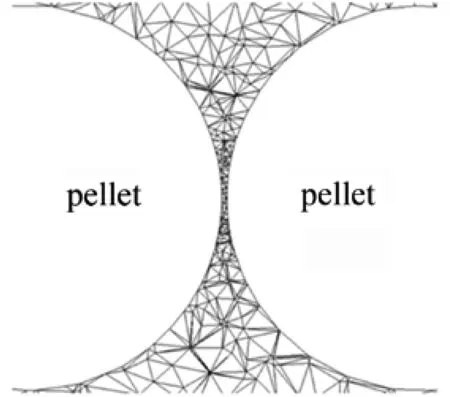
图4 颗粒间网格示意
1.2 数值模型
1.2.1 欧拉模型
欧拉方法对每一相求解动量方程和连续性方程,并通过相间作用力来实现相间耦合[15],能够有效地模拟相间混合,对于不可压缩流体来说,每一相的平均质量和动量方程表示如下:
(1)连续性方程
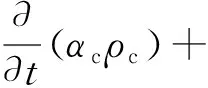
(1)
式中,α、ρ和u分别表示体积分数、密度和速度;下标c表示连续相的油或水。
(2)体积分数守恒方程
多孔介质通道中的油水两相流,只存在油相和水相,因此各自体积分数αs,αl任意时刻都服从:
αs+αl=1
(2)
(3)动量方程
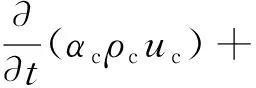
(3)
式中,G为重力;FM是两相间的转换动量或两相之间的作用力,包括曳力、升力、虚拟质量力和湍流耗散力;τ为应力张量;上标l和t分别表示层流和湍流。
1.2.2 湍流模型
Realizablek-ε湍流模型将流场的旋转以及弯曲壁面流动考虑在内,可用于中等强度旋流的流场。故本文选用Realizablek-ε湍流模型,其表达式为
(4)
(5)
式中,t表示时间,ρ表示密度,Gk与Gb均表示湍动能,YM表示湍流的脉动分量在运动过程中对耗算率的影响,ut表示湍流粘性系数。Clε与C2ε是常量,σk为湍动能的Prandtl数,σε是耗算率的Prandtl数。Clε=1.44,C2ε=1.29,σk=1.0,σε=1.2。
1.2.3 边界条件及求解器设置
边界条件设置如下:入口条件,设为速度边界条件,分别设置5%、30%、60%、90% 4组油水体积分数。当油水体积分数大于50%时,主相为油相,密度为730 kg/m3,动力粘度为2.4×10-3Pa·s;当油水体积分数小于50%时,主相为水相,密度为998.2 kg/m3,动力粘度为1×10-3Pa·s;出口条件,设为自由出流;压力条件,仅对油水两相进行数值模拟研究,不考虑气相,因此操作压力设为101.325 kPa,压力参考点设置在出口边界面,防止结果出现负压的情况;圆管对称边界面设置为symmetry边界条件;壁面无滑移,近壁面采用标准壁面函数处理。
采用pressure-based求解器以及适于压力和速度耦合的SIMPLE算法进行求解,各控制方程采用二阶迎风离散格式;为使计算结果收敛更快可适当调低松弛因子;监测残差设置为10-5。
2 结果与分析
2.1 模拟结果
图5为4种不同油水比工况下,等差值多孔介质长度下阻力压降的模拟值。可以看出,随着入口流速的增大,不同油水比之间的阻力压降差也变得更加显著,每段多孔介质中阻力压降随入口流速的增大呈指数式上升趋势,在入口流速较低时,即层流流态,油水混合液主要受黏性阻力,流速-阻力压降曲线呈一次函数曲线,当流速越大时,雷诺数超过一定临界值时,惯性阻力项主导流动阻力,流速-阻力压降曲线呈二次函数曲线。
(a)5%油水比
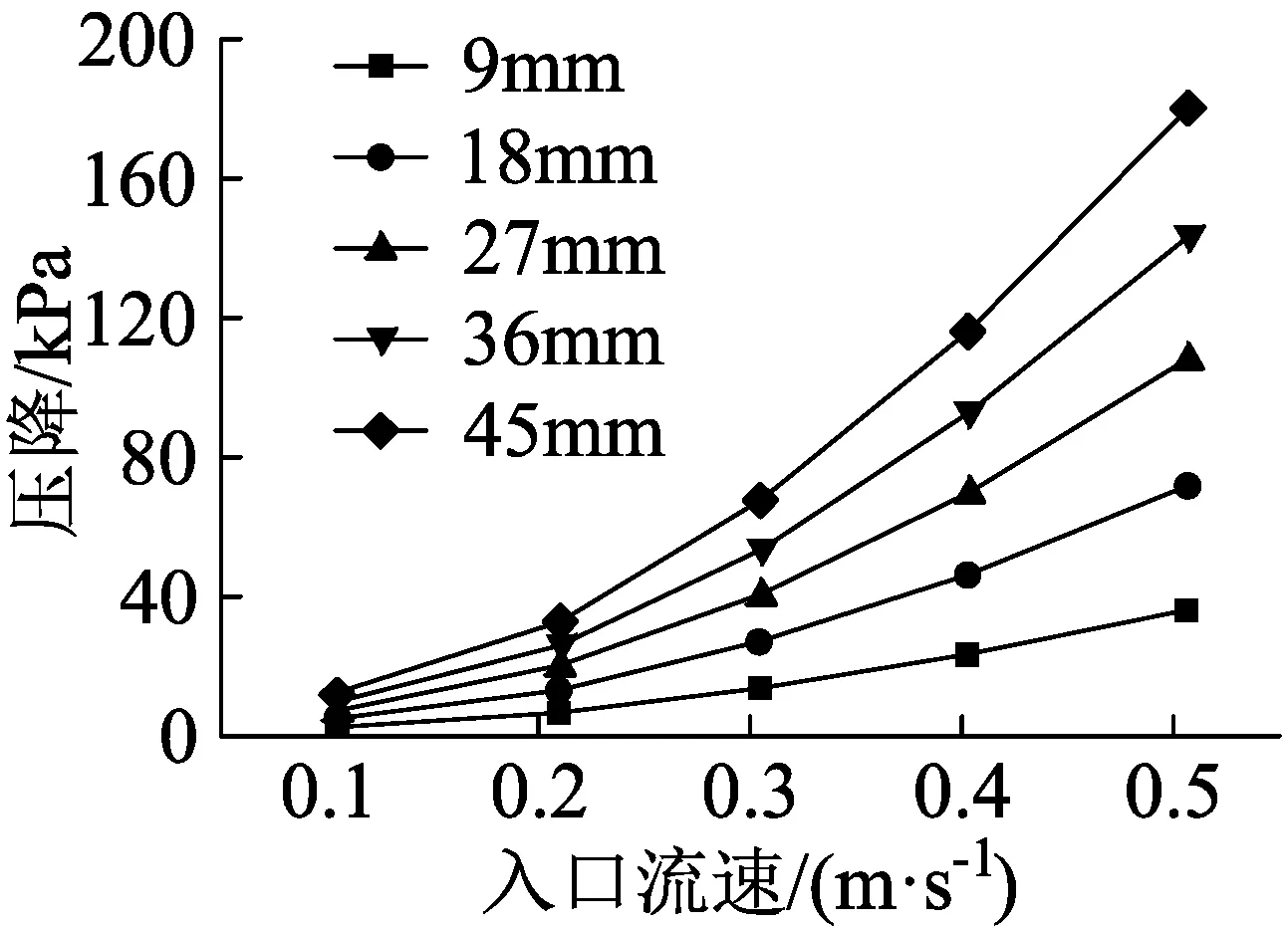
(b)30%油水比
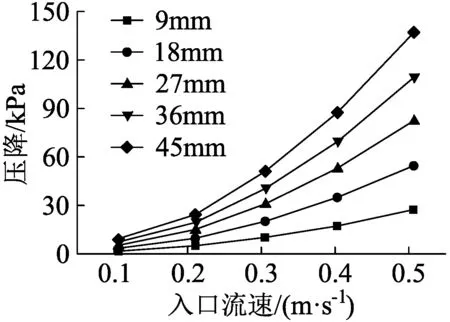
(c)60%油水比

(d)90%油水比图5 不同油水比下每段多孔介质的压降
2.2 油水比对多孔介质阻力压降的影响
图6是等体积分数差的油水混合液下,阻力压降随入口流速变化的模拟值。由图可以看出,入口流速较小时,不同油水比下的压降变化均较小,压降与流速均成一次函数关系,但随着入口流速的增大,阻力压降变化幅度也逐渐增大。按等体积分数改变油水比,入口流速为0.05 m/s时,阻力压降改变较小,5%油水比的最小压降与90%油水比的最小压降仅相差4 kPa,而随着入口流速增大,在0.5 m/s时,阻力压降产生巨大改变,5%油水比的最大压降与90%油水比的最大压降相差接近147 kPa。同时可以看出,油水比一定时,随入口流速的增大,流速-阻力压降曲线呈现二次函数曲线。
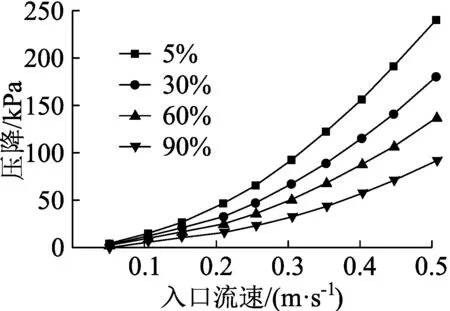
图6 不同油水比下入口流速与压降的关系
研究表明,相邻体积分数差值的油水比下,相同入口流速对应的阻力压降之间差距大致是相等的,说明在不同流速时,油水比的变化不会改变阻力压降上升的变化趋势,但油水比越小时,阻力压降值随流速变化得越快。
2.3 多孔介质通道长度对阻力压降的影响
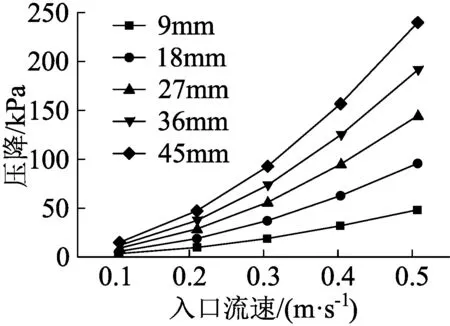
图7是以5%油水比工况为例,按等差值截取的多孔介质通道长度下,阻力压降随入口流速变化的模拟值。由图可以看出,入口流速较小时,不同多孔介质长度下的压降变化均较小,流速-阻力压降曲线均呈一次函数曲线关系。多孔介质长度较长时,随着入口流速的增大,阻力压降变化也逐渐增大。按等差值截取多孔介质长度,入口流速为0.05 m/s时,阻力压降改变较小,9 mm长度的最小压降与45 mm长度的最小压降仅相差3.4 kPa,而随着入口流速增大,在0.5 m/s时,阻力压降产生更大改变,9 mm长度的最大压降与45 mm长度的最大压降相差接近192 kPa。同时可以看出,多孔介质长度一定时,随入口流速的增大,阻力压降-流速曲线的斜率越大。这是由于流动阻力项中的黏性阻力项和惯性阻力项会随层流区和紊流区的流态变化,依次成为主导项。同时,从图7可以看出,相邻差值的多孔介质长度下,相同入口流速对应的阻力压降之间差距大致是相等的,说明在不同流速时,多孔介质长度的变化不能改变阻力压降上升的变化趋势。
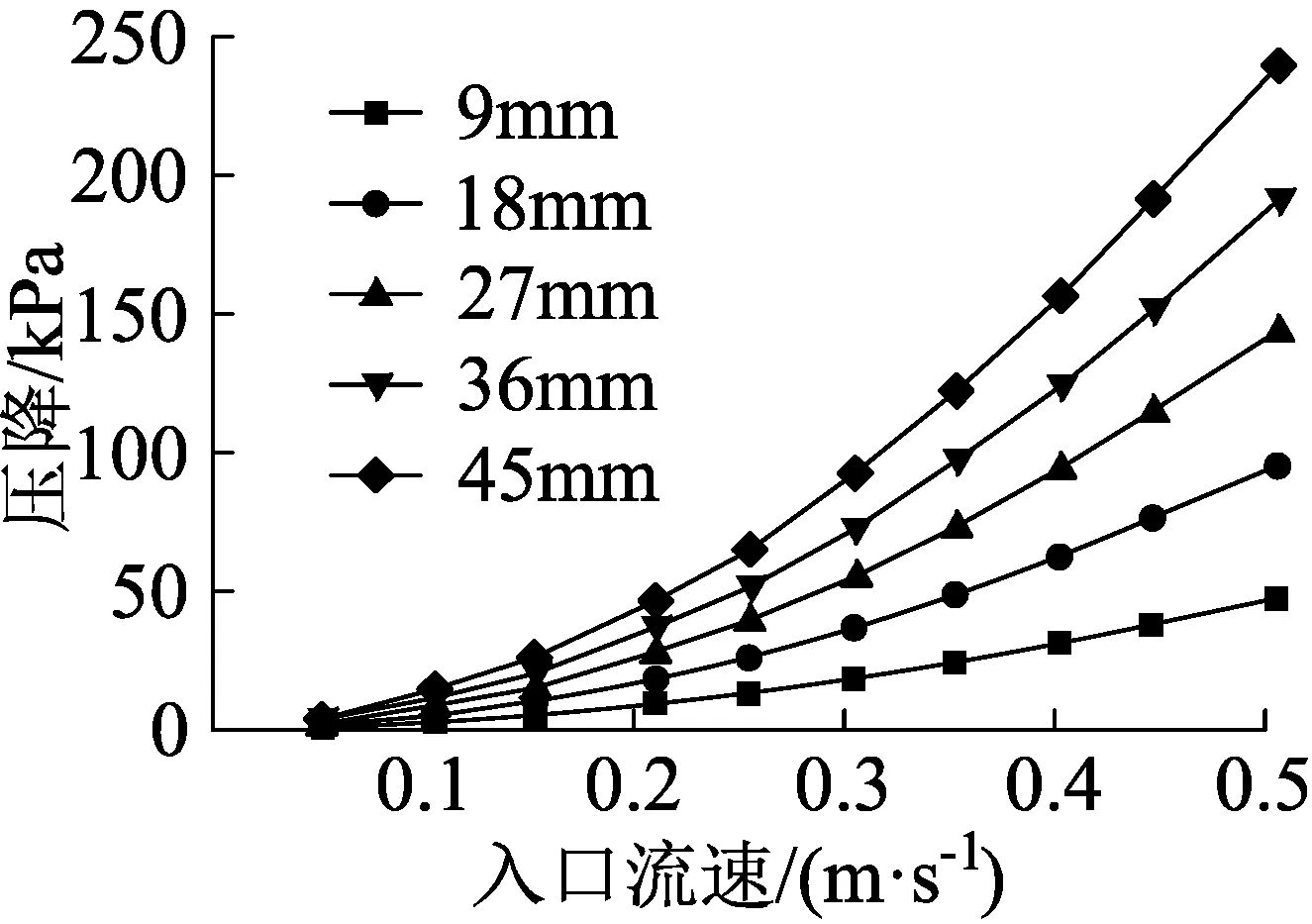
图7 不同多孔介质长度下入口流速与压降的关系
3 结论
通过油水两相在颗粒多孔介质中的流动阻力特性三维数值模拟研究,得到不同油水比和等差值多孔介质长度工况下,阻力压降的变化规律。
(1)不同入口流速下,油水比越大,多孔介质进出口阻力压降反而越小;当入口流速较低时,不同油水比下的进出口阻力压降相差较小,流速-阻力压降曲线呈一次函数曲线;随入口流速逐渐增大,不同油水比下的进出口阻力压降差值越显著,流速-阻力压降曲线呈二次函数曲线。
(2)不同入口流速下,多孔介质长度越长,多孔介质进出口阻力压降越大;当入口流速较低时,不同多孔介质长度下的进出口阻力压降相差较小,流速-阻力压降曲线呈一次函数曲线;随入口流速逐渐增大,不同多孔介质长度下的进出口阻力压降相差越大,流速-阻力压降曲线呈二次函数曲线。
(3)按等体积分数差改变油水比以及等差值截取多孔介质长度,在相同入口流速时,相邻工况的阻力压降差值大致相等。这说明入口流速一定时,油水比以及多孔介质长度的等差值改变并不能改变阻力压降的上升趋势。
