无相位远场数据反演散射障碍的神经网络方法

尹伟石, 杨文红, 曲福恒

(1. 长春理工大学 理学院, 长春 130022; 2. 长春理工大学 计算机科学技术学院, 长春 130022)

0 引 言

声波散射问题在雷达、 无损探伤、 医学成像等领域应用广泛, 目前已得到广泛关注. 声波散射问题分为正散射问题和反散射问题. 正散射问题是指对给定的入射波和散射体确定波场的散射特性, 反散射问题是根据波场的散射特性确定散射体的物理或几何信息. Kress等[1]提出并证明了无相位远场数据具有平移不变性, 因此利用无相位远场数据重构障碍物的位置十分困难； Zhang等[2]证明了两个不同方向的平面波叠加入射可打破无相位远场数据的平移不变性, 并用牛顿迭代法重构了障碍物形状； 文献[3-4]通过在散射系统中加入参考球, 打破了无相位远场数据的平移不变性； Sun等[5]提出了两个点源叠加入射可以克服无相位数据的平移不变性, 并给出了相应的证明. 这些方法使无相位远场数据的平移不变性得到解决. 目前, 关于无相位数据反演障碍物形状问题的研究已有很多结果： Shin[6]在足够高的频率下, 提出了利用无相位远场数据重构障碍物形状的迭代算法, 并通过数值实验证明了所提方法的有效性； Zhang等[7]提出了一种直接成像算法, 在固定频率下, 由多组不同方向的入射波和观测点产生的无相位远场数据重构障碍物的形状.

近年来, 神经网络方法在反散射问题中被广泛应用[8-13]. Li等[8]提出了一种几何体生成方法, 根据输入的特征参数生成几何体, 并通过数值实验证明了该方法可很好地重构几何体； Yin等[9]提出了一种序列对序列的神经网络方法, 使用无相位远场数据较好地恢复了障碍物的位置和形状. 在实际应用中, 远场数据的相位信息很难获取, 只能获取远场数据的强度或模(无相位远场数据), 本文考虑无相位远场数据恢复散射障碍问题, 提出一种两层门控循环单元(GRU)神经网络对门控循环单元神经网络的方法(MGNN), 并给出该方法的收敛性分析.

1 正问题

考虑二维声波散射问题, 对均匀介质中的不可穿透障碍物D⊂2, 总场u(x)∶=u(i)(x)+u(s)(x), 满足Helmholtz系统[14]:

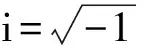
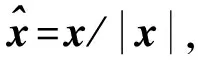
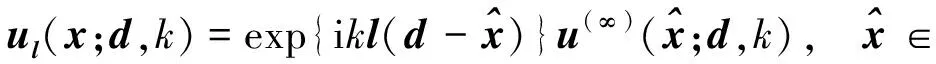
因此无法用无相位远场数据|u(∞)(x;d,k)|重构障碍物的位置和形状. 为打破无相位数据的平移不变性, 本文考虑用两组不同方向的平面波, 令

u(i)=u(i)(x;d1j,d2j,k)∶=exp{ikd1j·x}+exp{ikd2j·x},

(4)

2 MGNN模型构建

本文从机器学习的角度考虑无相位远场数据反演障碍物位置及形状问题.

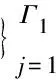
(5)

并定义x=(x(1),x(2),…,x(T))表示{λ11,λ12,…,λnj,…,λΓ1Γ2}, 其中T=Γ1Γ2.

假设1假设障碍物D的边界曲线有以下参数化形式：

∂D:z(t)=(z1(t),z2(t)), 0≤t≤2π,

其中z1(t),z2(t)用下列Fourier的截断形式表示:

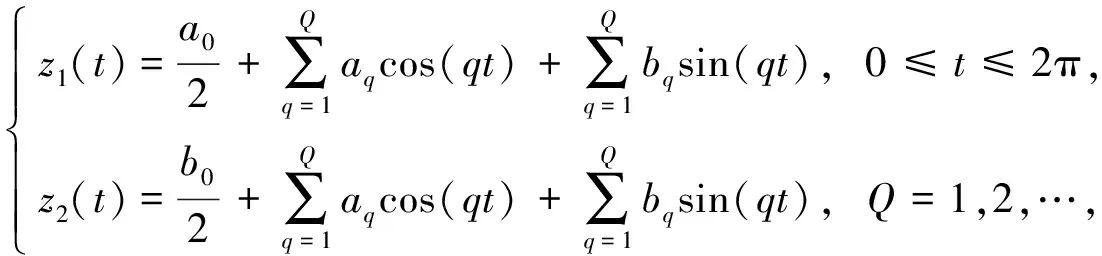
(6)

式中Q∈. 定义y=(y(1),y(2),…,y(M))表示式(6)的系数a0,b0,aq,bq,q=1,2,…,Q, 其中M=4Q+2.

2.1 模型构建

本文构建一种两层GRU神经网络对门控循环单元神经网络(MGNN)模型, 该模型由多个GRU神经网络构成. 在训练过程中,x=(x(1),x(2),…,x(T))为模型的输入,y=(y(1),y(2),…,y(M))为模型的输出. 对输入向量x=(x(1),x(2),…,x(T))中每个元素x(t)都先经过两层的GRU神经网络进行特征提取, 并将提取特征作为中间特征进行特征记忆, 再将记忆的特征与y(m)经过两层GRU神经网络进行训练学习, 从而完成整个神经网络模型的训练. 每个GRU神经网络的工作状态如图1所示.

图1 GRU神经网络示意图Fig.1 Schematic diagram of GRU neural network

GRU神经网络的工作过程由重置门和更新门控制, 图1中r(t)表示重置门,z(t)表示更新门. 实现过程如下：

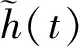
r(t)=S(Wr[x(t),h(t-1)]),

t时刻的候选状态为：

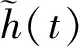
z(t)=S(Wz[x(t),h(t-1)]),

并计算出中间状态

3) 中间状态h(t)经过全连接层得到最终输出为y(t)=S(Wo·h(t)).

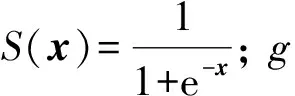
2.2 收敛性分析

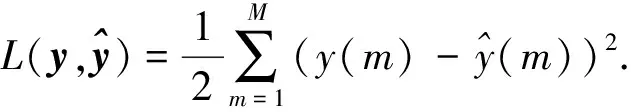
(7)

损失函数对权重的梯度为

(8)

更新模型即为更新模型中的权重和偏置.

神经网络第一层、 第二层、 第三层、 第四层的输入分别为

每层神经网络的输入向量为

定义3激活函数对于任意向量A=(a1,a2,…an)T, 有G(A)=(g(a1),g(a2),…,g(an))T, 定义

G′(A)=(g′(a1),g′(a2),…,g′(an))T,G″(A)=(g″(a1),g″(a2),…,g″(an))T.

第四层神经网络重置门的权重梯度为

由初始条件y(0)恒为0得

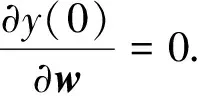
(10)

对任意给定的初始权重w0, 权重序列{wk}由以下迭代产生：

wk+1=wk+Δwk,

(11)

其中,

(12)

η>0是学习率.

假设2|g(r)|,|g′(r)|,|g″(r)|和|S(r)|,|S′(r)|,|S″(r)|对于r∈是一致有界的.

假设3|wk|(k=0,1,2,…)是一致有界的.

注1假设2和假设3对本文使用的S型激活函数及双曲正切激活函数有效, 且传统方法经常使用假设3进行非线性迭代[12-13], 以确保网络是收敛的.

定理1假设误差函数为式(7), 权重矩阵wt是由式(11)的任意初始权重w0生成的, 且权重矩阵wk二次连续可导, 则有：

1)E(wk+1)≤E(wk),k=0,1,2,…；

定理1表明建立的神经网络模型是收敛的.

注2由式(7),(8)可得

考虑不同迭代次数的权重{wk}, 并定义

引理1令Δv(4)(wk,m)=v(4)(wk+1,m)-v(4)(wk,m), 则

(13)

且当d=1时, 有

其中

θ(m-d)是Δv(wk,m)和Δv(wk+1,m)的中间量.

证明： 使用归纳法证明式(13), 首先考虑当m=1时,

Δv(wk,1)=wk+1u(4)(wk+1,1)-wku(4)(wk,1)=wk+1u(4)(wk,1)-wku(4)(wk,1)=u(4)(wk,1)Δwk

成立. 其次, 假设

成立, 则只需证明下式成立即可：

引理2若假设2和假设3成立, 则‖Δv(wk,t)‖≤C‖Δwk‖.

证明： 使用归纳法. 首先考虑当m=1时, 下式成立：

Δv(wk,1)=wk+1u(wk+1,1)-wku(wk,1)=wk+1u(wk,1)-wku(wk,1)=Δwku(wk,1)≤C‖Δwk‖.

假设‖Δv(wk,m)‖≤C‖Δwk‖成立, 则只需证下式成立即可：

同理可证对四层神经网络的权重也成立.

下面证明定理1. 应用Taylor展开式(7),(8),(12)以及注2、 引理1和引理2, 有

其中,

τ(m-d)是Δv(wk,m)和Δv(wk+1,m)的中间量. 根据假设1、 假设2、 注2、 引理1和引理2及Cauchy-Schwarz不等式, 有|ρ(wk)|≤C‖Δwk‖2, 因此L(wk+1)-L(wk)≤-(η-C)‖Δwk‖2, 若学习率足够小且满足0<η<1/C(C是常数), 则结论1)成立.

3 数值实验

下面通过数值实例说明建立的模型可应用于无相位远场数据重构障碍物的形状, 并通过数值实验验证本文提出的神经网络模型收敛.

3.1 数据集的构造

数据集的构造是机器学习解决反散射问题的基础, 本文构造无相位远场数据与形状参数的数据集. 障碍物D对应的数据由定义1的无相位远场数据XD=(XD(1),XD(2),…,XD(T))和假设1的形状参数YD=(YD(1),YD(2),…,YD(M))构成. 因此, 引入训练数据集

T={(XD,YD);D∈D},

(14)

其中D表示形状集合. 首先, 对给定的形状D, 使用积分方程方法[14]求解系统(1)-(3), 以获得相关的无相远场数据. 其次, 为排除自交边界曲线和参数为零的情形, 将式(6)系数(均匀分布在[-α,α]内,α∈+为给定的先验常数)用随机森林算法[15]进行分类处理. 即在第一阶段, 训练网络以识别其属于障碍的类别; 在第二阶段, 在给定的障碍类别内, 通过给定其无相远场数据, 训练网络以恢复未知障碍的相应Fourier系数.

3.2 数值算例

假设：

1) 入射波u(i)=u(i)(x;d1j,d2j,k)(j=1,2), 两组不同入射方向的夹角均为π/3；

2) 用实线表示障碍物的精确边界, 虚线表示障碍物的预测边界；

3) 障碍物的无相位远场数据均由波数k=1.1,2.1计算产生的无相位远场数据拼接而成；

4) GRU神经网络的神经元个数一般设为2p(p∈+), 通过大量实验确定模型中的参数. 模型中GRU神经元个数为256个, Dropout为0.5, 批量处理(Batch)为800, 迭代次数(Epoch)为50.

图2 花生形状重构Fig.2 Reconstruction of peanut shape

图3 风筝形状重构Fig.3 Reconstruction of kite shape

其次, 分别对Γ1,Γ2=5的数据集加入5%,10%,20%的噪声(均值为0、 方差为0.05,0.1,0.2的高斯白噪声), 对花生和风筝形状进行反演, 结果分别如图4和图5所示. 其中, 图4(A)～(C)和图5(A)～(C)分别表示加5%,10%,20%噪声的训练数据集训练网络预测的花生形状和风筝形状. 由图4和图5可见: 加10%以下噪声时对花生和风筝形状的反演结果无明显影响； 当增加到20%噪声时, 反演的障碍物曲线与真实曲线发生偏离. 图6(A)，(B)分别为针对花生形状和风筝形状迭代次数绘制的损失函数曲线(针对Γ1,Γ2=5的网络). 图6结果验证了网络的收敛性. 对入射方向及观测方向Γ1,Γ2=5产生的无相位远场数据, 分别选取训练样本集为2万个样本和5万个样本进行花生形状重构实验, 结果如图7所示. 由图7可见, 增加数据集的大小, 可使反演结果更好.

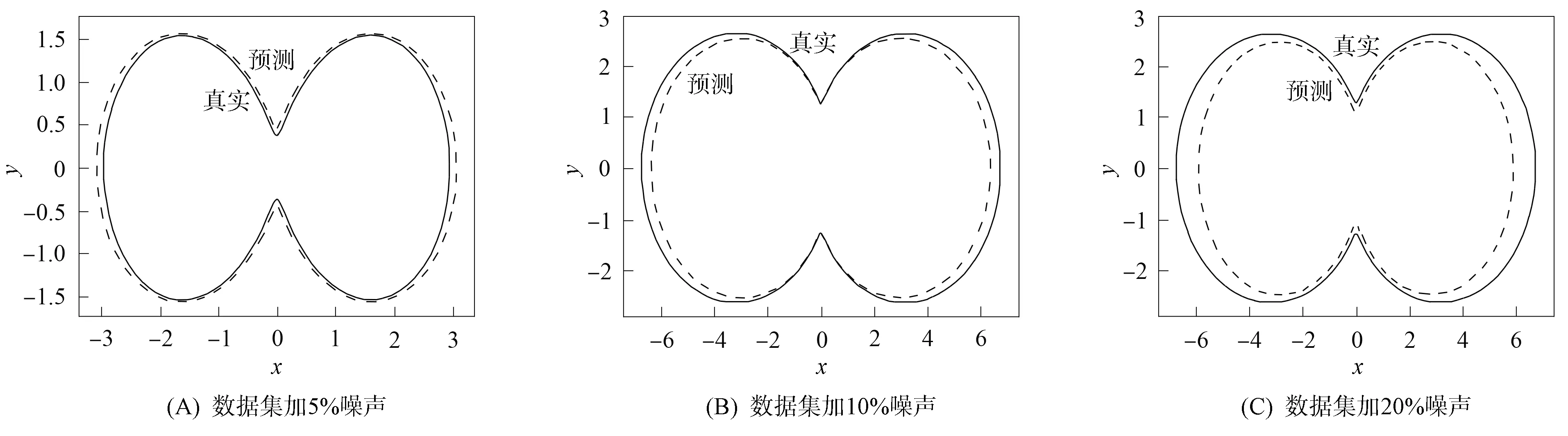
图4 加噪数据对花生形状重构效果Fig.4 Reconstruction effects of peanut shape with noisy data

图5 加噪数据对风筝形状重构效果Fig.5 Reconstruction effects of kite shape with noisy data

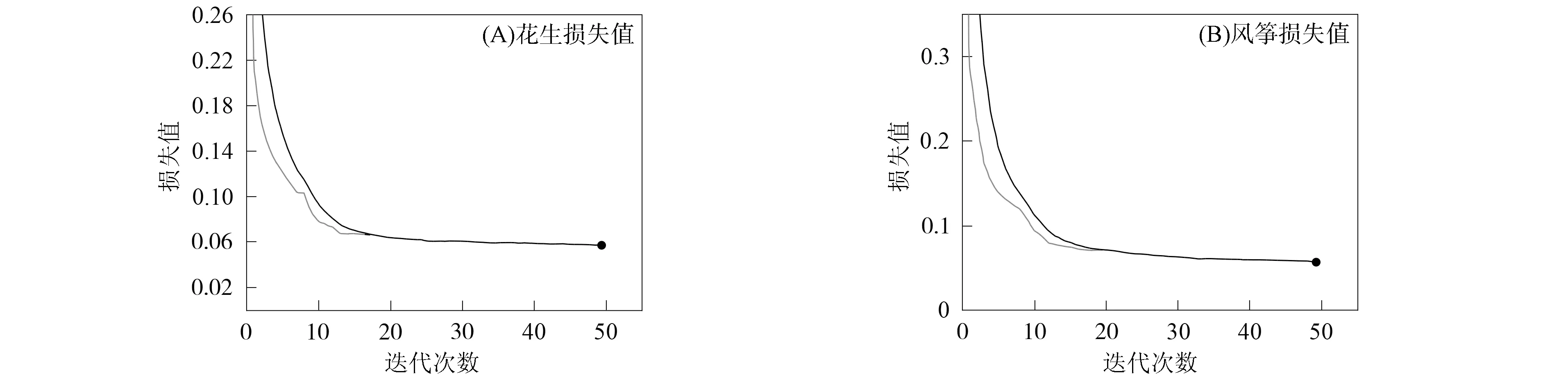
图6 迭代损失曲线Fig.6 Curves of iteration loss

图7 2万样本数据集(A)和5万样本数据集(B)的花生形状重构效果Fig.7 Reconstruction effects of peanut shapes data sets with 20 000 (A) and 50 000 (B) samples

综上可见, 两层GRU神经网络对GRU神经网络的方法能有效恢复散射障碍的位置和形状, 本文从理论和数值实验两方面说明了算法的收敛性, 为无相位反散射问题提供了一种新的计算方法.