NSD序列部分和乘积的渐近分布

赵珈玉, 陆冬梅

(长春理工大学光电信息学院, 长春 130114)

1 引言与主要结果

随机变量的极限理论主要研究中心极限定理、 大数定律和重对数律等. 目前, 关于随机变量序列部分和乘积渐近分布的研究受到广泛关注[1-25]. 文献[1]考虑均值为1的独立同分布指数随机变量序列{Xn,n≥1}, 得到了

(1)

利用Stirling公式, 式(1)等价于

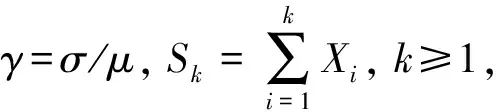
(2)

文献[3-4]讨论了随机变量序列属于参数α∈(1,2]的稳定分布的吸引域; 文献[5-9]分别对NA(negatively associated)序列部分和乘积、φ混合序列部分和乘积、 LNQD(liear negative quadrant dependent),LPQD(liear positive quadrant dependent)序列部分和乘积、 强混合序列部分和乘积、 NA序列部分和随机乘积进行讨论, 得到了类似定理1的结果. 而关于负超可加相依(negatively superadditive dependent, NSD)序列部分和乘积的极限分布研究目前尚未见文献报道. 基于此, 本文考虑NSD序列, 在同分布和严平稳两种情形下分别讨论其部分和乘积的渐近分布.

定义1[10]如果对任意的x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈n, 都有

φ(x∨y)+φ(x∧y)≥φ(x)+φ(y),

则函数φ:n→称为超可加的. 其中:

x∨y=(max{x1,y1},…,max{xn,yn});x∧y=(min{x1,y1},…,min{xn,yn}).

定义2[10]如果随机向量X=(X1,X2,…,Xn)满足:

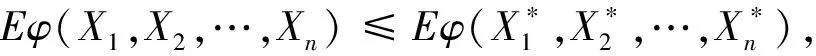
(3)

文献[10]给出了NSD随机变量的相关性质, 并举例说明椭球等高分布、 排列分布、 多项分布、 多元超几何分布、 Dirichlet分布等在一定条件下, 都具有NSD序列的性质, 同时指出由NSD随机变量不能推出NA随机变量. 文献[11]证明了NA随机变量能推出NSD随机变量, 表明NSD序列是包含独立和NA序列在内的一类更广泛的相依序列. 因此研究NSD序列的极限理论具有一定的理论意义和应用价值. 下面给出本文的主要结果.

则

(4)

1) 对某个ε>0，有|Cov(X1,Xn+1)|=O(n-1(logn)-2-ε);

则

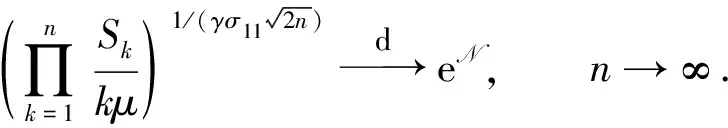
(5)

由于NSD序列包含独立和NA序列, 因此有:

推论1设{Xn,n≥1}是一列同分布(或严平稳)正的NA序列, 满足定理2(或定理3)的条件, 则式(4),(5)成立.

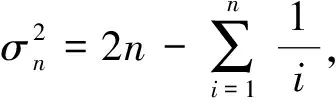
2 定理的证明

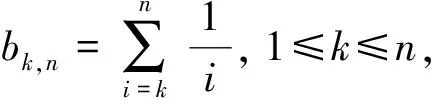
引理1[10]如果(X1,X2,…,Xn)是NSD的,g1,g2,…,gn均为非降函数, 则(g1(X1),g2(X2),…,gn(Xn))也是NSD的.

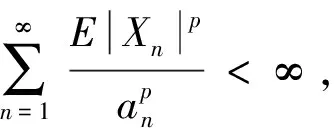
引理3[16]设{Xn;n≥1}为一NSD序列, {ak,n, 1≤k≤n,n≥1}为一实值的三角阵列, 满足下列条件：

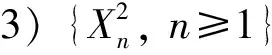
则

引理4在定理2的条件下, 有

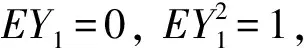
因此引理3的条件均满足, 故由引理3可得

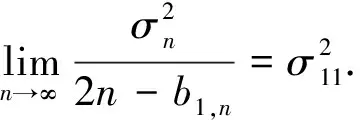
由定理3中条件1)及bi,n≤Clogn, 可得

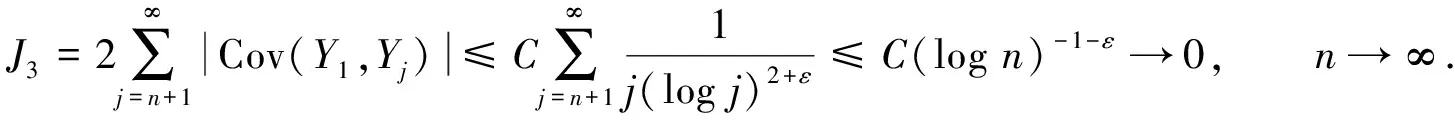
(8)

下面证明J2→0, 首先有

进一步, 由定理3中条件1)可知

最后由式(6)～(9)可知结论成立.

2.1 定理2的证明

当x>-1时, 有log(1+x)=x+xθ(x), 其中当x→0时,θ(x)→0.则有

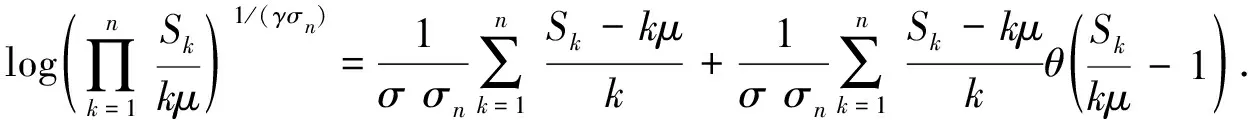
(10)

从而

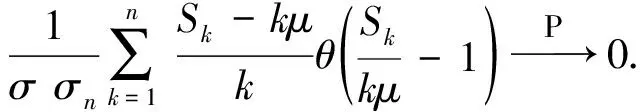
(11)

由引理4可知

(12)

于是由式(10)～(13)及Slutsky定理可知定理2成立.

2.2 定理3的证明

利用引理2～引理5, 类似定理2的证明可知定理3成立.