带有非线性边界条件的弱衰退记忆型非自治经典反应扩散方程解的渐近性

汪 璇, 梁玉婷

(西北师范大学 数学与统计学院, 兰州 730070)

0 引 言

在非线性边界条件下, 考虑下列弱衰退记忆型非自治经典反应扩散方程解的长时间动力学行为:

(1)

其中Ω为3上带有光滑边界Γ的有界域. 关于外力项h, 仅设;L2(Ω))(即平移有界), 且H (h0)=[h0(x,s+h)|h∈其中[·]表示h0(x,s+h)关于空间;L2(Ω))弱收敛拓扑的闭包. 若h∈H (h0), 则其中‖·‖表示L2(Ω)范数.

借助u(·)和记忆核函数k(·)的线性卷积项, 体现了历史外力在弱衰退记忆影响下在能量耗散中的作用. 系统的能量耗散不仅受现时外力的影响, 而且还受历史外力的影响, 并随着时间的推移历史外力的影响越来越小. 因此, ∀s∈+, 设记忆核函数k(·)∈C2(+),k(s)≥0,k′(s)≤0,k(∞)=0. 参考文献[1], 引入反应过去历史的新变量ηt(x,s)=u(x,t-r)dr,s≥0, 则

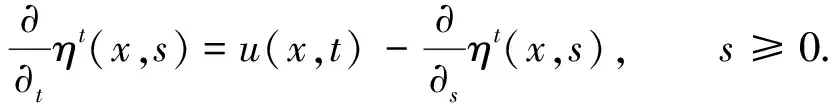
(2)

μ∈C1(+)∩L1(+),μ(s)≥0,μ′(s)≤0, ∀s∈+,

(3)

μ′(s)+δμ(s)≤0, ∀s≥0,

(4)

其中δ>0. 因此方程(1)可转化为

(5)

相应的初值条件为

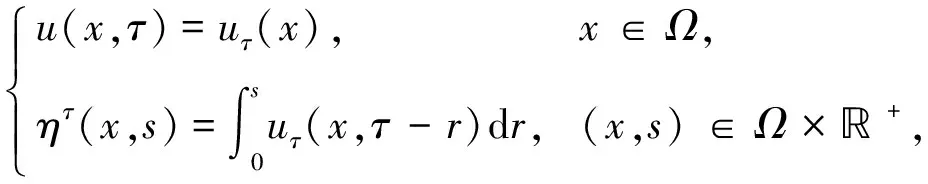
(6)

边值条件为

(7)

其中,u(·)满足下列条件: 存在正常数N0和β=δ/2, 使得

(8)

问题(5)-(7)所包含的非线性项分为两类: 内部非线性项f和边界非线性项g. 设其均为C1函数且满足: 存在正常数l,m, 使得

f′(s)≥-l, ∀s∈,

(9)

g′(s)≥-m, ∀s∈,

(10)

且

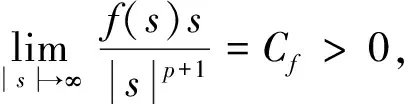
(11)

(12)

其中p,q∈+且p>1,q>1.

进一步, 为了保证问题(5)-(7)对应的动力系统为能量耗散系统, 设其内部非线性项和边界非线性项满足如下平衡条件之一:

1)p+1=2q;

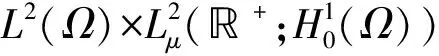
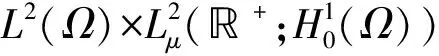
1 预备知识

〈·,·〉D(As/2)=〈As/2·,As/2·〉, ‖·‖D(As/2)=‖As/2·‖,

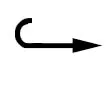
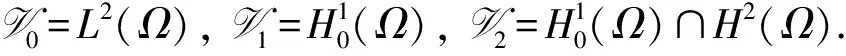
引理2[13]存在常数C0(Ω,1)>0, 使得对任意的φ∈W1,1(Ω), 有

引理3设{Uσ(t,τ),t≥τ,σ∈Σ}为作用于Banach空间(X,‖·‖)上的过程族, 则对于平移半群{T(h)}h≥0, 下列平移恒等式成立:

UT(h)σ(t,τ)=Uσ(t+h,τ+h), ∀h≥0, ∀t≥τ,τ∈.

(13)

若过程族{Uσ(t,τ),σ∈Σ}拥有一致(w.r.t.σ∈Σ)有界吸收集B0, 并对任意的ε>0, 存在T=T(B0,ε)和φT(·,·;·,·)∈C(B0×Σ), 使得

‖Uσ1(T,τ)x-Uσ2(T,τ)y‖≤ε+φT(x,y;σ1,σ2), ∀x,y∈B0, ∀σ1,σ2∈Σ,

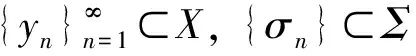
定义2[16]若对固定的τ,t≥τ,τ∈,zτn→zτ于X及hn⇀h于Σ, 有Uhn(t,τ)znτ⇀Uh(t,τ)zτ于X. 则称作用于X的过程族{Uσ(t,τ),σ∈Σ}为(X×Σ,X)-弱连续.

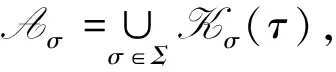
2 主要结果

2.1 解的存在唯一性

定义3记I=[τ,T], ∀T>τ. 设h∈H (h0),g∈L2(Ω)且zτ∈N0. 二元组z=(u,ηt)满足:

1)u∈L2(I;H0)∩(L2(I;H1)∩Lp+1(I;Lp+1(Ω)))×Lq+1(I;Lq+1(Γ));

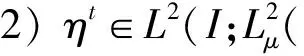
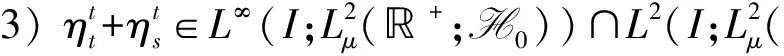
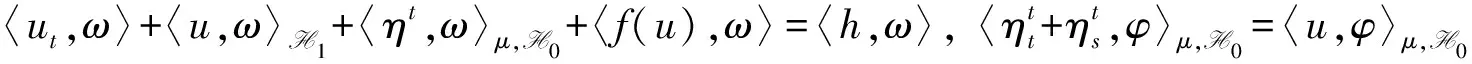
用文献[12,17]的Galerkin逼近方法, 可得问题(5)-(7)的解z(t)在N1中的存在唯一性:

其中当s→0+时,Q(·)→0.

根据定理2, 对任意的h∈H(h0), 可定义问题(5)-(7)在空间N1中的解过程, 即

且Uh(t,τ)(h∈H (h0))为作用于N1上的过程族.

2.2 有界吸收集的存在性

首先, 给出问题(5)-(7)的解在空间N1中的先验估计.

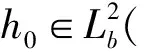
证明: 将方程(5)乘以u并在L2(Ω)上积分, 得

(14)

又

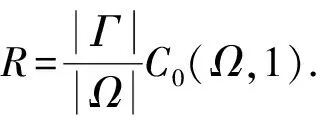
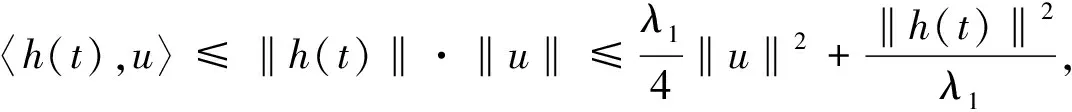
(17)

将上述估计代入式(14), 可得

应用Poincaré不等式, 可得

(19)

其中C3=C2|Ω|.

取β1=min{λ1,δ}, 有

(20)

应用Gronwall引理, 可得

并且

故

(23)

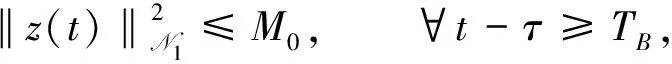
(24)

证毕.

根据引理5可得有界吸收集的存在性:

定理3(有界一致吸收集存在定理) 若引理5的假设成立, 则对任意有界子集B⊂N1, 存在Tτ=Tτ(‖B‖N1), 使得对所有的t-τ≥TB且zτ∈B, 有‖Uh(t,τ)zτ‖≤M0.

2.3 一致吸引子的存在性

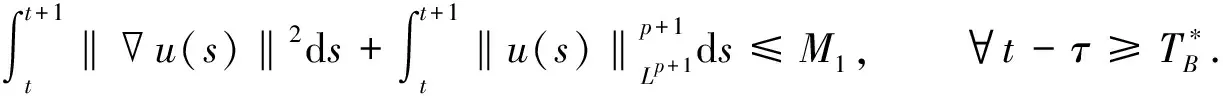
(25)

证明: 对式(18)在[t,t+1]上积分, 并利用式(24), 可得

故式(25)成立, 证毕.

根据无穷维动力系统一致吸引子的存在性定理(定理1), 还需验证过程族{Uh(t,τ),h∈H (h0)}在N1中的渐近紧性.

(26)

相应的边值条件为

(27)

初值条件为

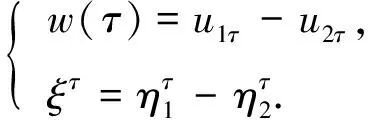
(28)

将式(26)乘w(t)并在Ω上积分, 可得

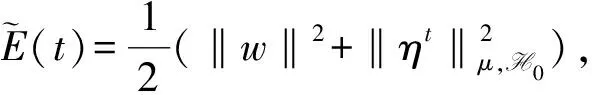
根据式(9), 可得-〈f(u1)-f(u2),w〉≤l‖w‖2. 类似式(16)的估计并根据式(11), 可得

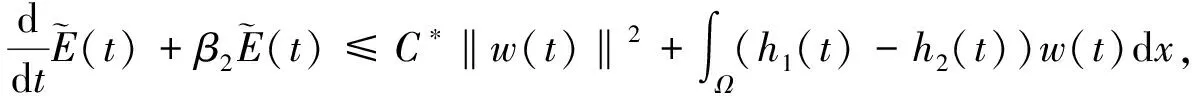
(30)

对任意给定的T>τ, 将式(30)乘eβ2t并在[τ,T]上积分, 有

(31)

对应于引理3, 设

(32)

A∶={u(t),t∈[τ,T]:u(t)=Π1Uh(t,τ)zτ,zτ∈B0,h∈H (h0)}

在L2([τ,T];L2(Ω))中相对紧.

首先, 关于式(18)在[τ,T]上积分并利用式(24), 可得

则A在L2([τ,T];H1)∩Lp([τ,T];Lp(Ω))中有界.

其次, 利用式(5)有

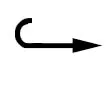
最后, 对任意的v∈L2(Ω), 有

其中

综上, 根据引理3和定理2可知, {Uh(t,τ),h∈H (h0)}在N1中一致渐近紧.

引理7[18]设X是自反的Banach空间,xn⇀0∈X. 则对每个紧(在X*中)子集B⊂X*, 下列结论一致收敛成立: 对任意的ε>0, 存在仅依赖ε的常数Nε, 使得对任意的n≥Nε及f∈B, 有|〈f,xn〉X*|≤ε成立.

引理3表明, 与方程(1)相对应的过程族{Uσ(t,τ),σ∈Σ}具有紧的(在X中)一致(σ∈Σ)吸收集, 且在X中有界, 因此, 本文得到了紧的一致(σ∈Σ)吸引子A的存在性, A⊂X.

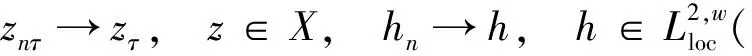
(34)

由于方程(5)在Lq([τ,T];H-γ(Ω))(q为式(9)中p的共轭)中成立, 则对任意固定的T(>τ), 有

其中u=Π1Uh(t,τ)zτ∈L2([τ,t];L2(Ω)),Π1是X×Σ到X的映射. 因为A在X中是有界的, 因此由定理3可知, 存在M使得

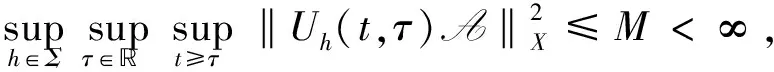
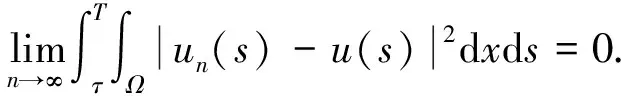
(35)

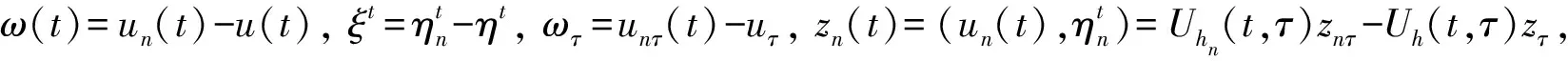
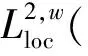
是L2([τ,t];L2(Ω))上的一致紧子集(直接应用引理7即可), 从而完成了过程族{Uσ(t,τ),σ∈Σ}为(X×Σ,X)-弱连续的证明.

根据引理2、 定理3和定理4, 可得本文的主要结果:

定理5设{Uh(t,τ),h∈H (h0)}为问题(5)-(7)在能量空间N1的解生成的过程族. 如果定理4的假设成立, 则过程族{Uh(t,τ),h∈H (h0)}在空间N1中拥有紧的一致吸引子AH (h0). 进一步, 有

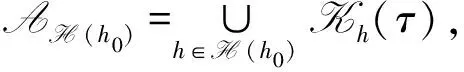
其中Kh(τ)为过程族{Uh(t,τ),h∈H (h0)}的核Kh在t=τ时刻的核截片.