半结合3-李代数的结构

白瑞蒲, 张 艳

(河北大学 数学与信息科学学院, 河北 保定 071002)

0 引 言

3-元代数系统在数学和物理的相关领域应用广泛. 例如: 3-李代数[1-2]广泛应用于可积系统与Nambu力学系统[3-8]; Pre-3-李代数和局部上循环3-李双代数[9-10]的结构与3-李代数中Yang-Baxter方程的解紧密相关； 基于3个变量(记为x,y,z)的经典Nambu括号[4], 利用了偏微分中类似Jacobi行列式定义乘积:

且满足3-李代数的Filippov等式:

{A,B,{C,D,E}}={{A,B,C},D,E}+{C,{A,B,D},E}+{C,D,{A,B,E}}.

文献[10]利用非交换算子实现的3-元代数具有乘积:

[A,B,C]=A[B,C]+B[C,A]+C[A,B]=[B,C]A+[C,A]B+[A,B]C.

虽然3-元运算不满足Filippov等式, 但3-代数应用广泛. 因此, 很多研究者利用已知的代数结构构造3-元代数结构, 并研究其应用及与3-李代数的关系. 本文构造一类不满足完全结合律和完全交换律的代数系统, 称为半结合3-代数, 并研究其基本结构. 若无特殊说明, 本文讨论的代数及线性空间的基域 F是特征为零的域, 对线性空间V的子集S, 〈S〉表示由S张成的子空间. 对给定的代数A, 列出A在一组基下的乘法表时, 省略了乘积为零的基向量运算.

1 半结合3-代数的定义及基本结构

定义1半结合3-代数(A,{,,})是具有3-元线性运算{,,}:A⊗A⊗A→A的线性空间A, 且满足∀xi∈A, 1≤i≤5, 有

对A的子空间B1,B2,B3, 记{B1,B2,B3}为由{x1,x2,x3}(∀xi∈Bi,i=1,2,3)张成的子空间, {A,A,A}记为A1, 称为A的导代数. 如果A1=0, 则称A为Abel的.

例如, 设A为具有一组基v1,v2,v3的3-维线性空间, 则A按下列乘法构成半结合3-代数: {v1,v2,v2}=-{v2,v1,v2}=v3, 其余运算为0.

定义2设B是半结合3-代数A的子空间, 如果B满足{B,B,B}⊆B, 则称B是A的子代数. 如果B满足{A,A,B}⊆B且{A,B,A}⊆B, 则B称为A的理想.

显然, {0}和A是A的理想, 称为A的平凡理想. 如果A没有真理想, 则称A是单半结合3-代数.

对给定A的子空间V, 子代数

ZA(V)={x|x∈A, {x,V,A}={V,A,x}=0}

称为V在A中的中心化子.ZA(A)称为A的中心, 简记为Z(A), 即

Z(A)={x|x∈A, {x,A,A}={A,A,x}=0}.

易见Z(A)是A的理想.

定义3设A和A1是两个半结合3-代数. 如果线性映射(线性同构)f:A→A1满足

f{x,y,z}={f(x),f(y),f(z)}, ∀x,y,z∈A,

则称f是代数同态(代数同构).

设I是A的理想,A/I={x+I|x∈A}是商空间, 则A/I按下列运算构成半结合3-代数:

{x+I,y+I,z+I}={x,y,z}+I, ∀x,y,z∈A,

称为A关于I的商代数. 显然, 自然映射π:A→A/I,π(x)=x+I(∀x∈A)是满的代数同态.

命题1设A是半结合3-代数,I1,I2,I3是A的理想, 则下列结论成立:

1)I1+I2,I1∩I2和{I1,I2,I3}是A的理想;

2) 如果I1⊆I2, 则I2/I1是A/I1的理想.

证明: 由定义可直接验证, 故略.

命题2设A和A1是半结合3-代数,f:A→A1是代数同态, 则下列结论成立:

1)K=Kerf={x∈A|f(x)=0}是A的理想,f(A)是A1的子代数;

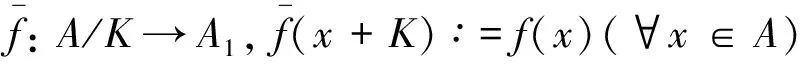
证明: 因为f:A→A1是代数同态, 则∀x∈K=Kerf, 有

所以K是A的理想. 直接计算可知f(A)是A1的子代数. 对任意子代数B1≤A1,B=f-1(B1)是A的满足K≤B的子代数, 且B1是A1的理想当且仅当B=f-1(B1)是A的理想. 结论得证.

定理1设A是半结合3-代数, 则下列结论成立:

1) 如果存在非零向量e1,e2,e3,e4∈A, 使得{e1,e2,e3}=e4, 则e4≠λes, 其中:λ∈F,λ≠0;s=1,2,3.

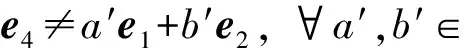
证明: 如果e4=λe1,λ∈F,λ≠0, 则由式(1),(2)有

矛盾. 如果e4=αe3,α∈F,α≠0, 则有

矛盾. 结论1)得证.

如果存在非零向量e1,e2,e3∈A, 使得{e1,e2,e3}=λe1+μe2≠0(λ,μ∈F). 不失一般性, 假设μ≠0, 则

矛盾. 所以∀λ,μ∈F, {e1,e2,e3}≠λe1+μe2, 结论得证.

定理2设A是非Abel的m-维半结合3-代数,m≥3, 则存在线性无关向量ei,ej,ek∈A, 使得{ei,ej,ek}≠0.

证明: 因为A是非Abel的, 故由式(1)知存在线性无关的向量e1,e2∈A, 使得{e1,e2,A}≠0. 设{e1,e2,…,em}是A的一组基. 如果{e1,e2,el}=0(∀l≥3), 则存在a,b∈F, 使得{e1,e2,ae1+be2}≠0. 所以{e1,e2,ae1+be2+e3}≠0, 且e1,e2,ae1+be2+e3线性无关. 结论得证.

定理3设A是s-维半结合3-代数,s≤6, 则A1⊆Z(A).

证明: 只需证明{A,A1,A}={A,A,A1}=0. 对任意非零向量el∈A1, 存在非零向量ei,ej,ek∈A, 使得{ei,ej,ek}=el.

1) 如果ei,ej,ek线性相关, 则可假设ek=aei+bej,a,b∈F,el=a{ei,ej,ei}+b{ei,ej,ej}. 对任意em,en∈A, 由式(2),(3), 有

所以{A,el,A}={A,A,el}=0.

2) 如果ei,ej,ek线性无关, 则可分如下两种情形讨论.

① 如果ei,ej,ek,el线性相关, 则el=aei+bej+cek, {ei,ej,ek}=aei+bej+cek,a,b,c∈F. 由定理1,ac≠0或bc≠0. 不失一般性, 假设ac≠0, 则

所以

② 如果ei,ej,ek,el线性无关, 则若dimA=4, 则{ei,ej,ek,el}是A的一组基. 对∀em,en∈A, 设

em=a1ei+b1ej+c1ek+d1el,en=a2ei+b2ej+c2ek+d2el,ai,bi,ci,di∈F,i=1,2.

则

类似上述讨论可知{em,en,el}=0.

若dimA=5, 可假设{ei,ej,ek,el,et}是A的一组基. 类似当dimA=4时的讨论, 只需证明{et,el,et}=0. 由式(1)～(3)可知

{et,el,et}={et,{ei,ej,ek},et}={et,{ej,et,ek},ei}=-{et,et,{ej,ek,ei}}=0.

若dimA=6, 设e1,e2,e3,e4,e5,e6是A的一组基, 其中e1=ei,e2=ej,e3=ek,e4=el. 则{e1,e2,e3}=e4. 类似上述讨论可得

{B,e4,B}={B,B,e4}=0, {C,e4,C}={C,C,e4}=0,

(4)

其中:B=〈e1,e2,e3,e4,e5〉;C=〈e1,e2,e3,e4,e6〉. 所以, 下面仅需讨论3个乘积： {e5,e4,e6},{e6,e4,e5},{e5,e6,e4}. 假设

{e5,e4,e6}=a3e1+b3e2+c3e3+d3e4+λ3e5+μ3e6,a3,b3,c3,λ3,μ3∈F，

由式(4),

λ3{e5,e4,e6}={{e5,e4,e6}-a3e1-b3e2-c3e3-d3e4-μ3e6,e4,e6}=0.

所以

直接计算可知μ3=0. 所以{e5,e4,e6}=a3e1+b3e2+c3e3+d3e4. 再由式(1),(2), 有

a3e4=a3{e1,e2,e3}={{e5,e4,e6}-b3e2-c3e3-d3e4,e2,e3}=c3{e2,e3,e3},

a3{a3e1+b3e2+c3e3+d3e4}={e5,c3{e2,e3,e3},e6}=c3{e5,e2,{e3,e3,e6}}=0,

得a3=b3=c3=0. 由定理1,d3=0, 即{e5,e4,e6}=0. 所以{e5,e6,e4}={e6,e4,e5}=0, 且A1⊆Z(A). 结论得证.

2 半结合3-代数的导子与型心

2.1 半结合3-代数的导子

定义4设A是半结合3-代数,D:A→A是线性映射. 如果D满足

D{x1,x2,x3}={Dx1,x2,x3}+{x1,Dx2,x3}+{x1,x2,Dx3}, ∀x1,x2,x3∈A,

(5)

则称D是A的导子.A的导子全体记为DerA.

命题3设A是半结合3-代数, 则DerA是一般线性李代数gl(A)的子代数.

证明: 直接计算可得结果.

对D∈DerA, 如果D满足D(A)⊆Z(A), 且D(A1)=0, 则称D是中心导子. 记Derc(A)为A的中心导子全体. 显然, DercA是DerA的子代数.

任取x1,x2∈A, 定义线性映射L(x1,x2),R(x1,x2),S(x1,x2):A×A→A,

L(x1,x2)(x)={x1,x2,x},R(x1,x2)(x)={x,x1,x2}, ∀x∈A,

(6)

S(x1,x2)=L(x1,x2)-R(x1,x2).

(7)

L(x1,x2)和R(x1,x2)分别称为由x1,x2确定的左乘映射和右乘映射.

定理4设A是半结合3-代数, 则对任意x1,x2,x3,x4∈A, 有

证明: 由式(1)～(3)可得式(8)～(10). 下面只需证明式(11),(12)成立. 对任意xi∈A(1≤i≤5), 由定义易见下列等式成立:

L(x1,x2)L(x3,x4)(x5)-L(x3,x1)L(x2,x4)(x5)=0,

L(x1,x2)L(x3,x4)(x5)-(L(x4,x2)R(x3,x1)(x5)+L(x3,x1)R(x4,x2)(x5))=0.

因此,

R(x3,x4)(R(x1,x2)+R(x2,x1))=0,

L(x1,x2)L(x3,x4)=L(x3,x1)L(x2,x4) =L(x4,x2)R(x3,x1)+L(x3,x1)R(x4,x2)

成立. 证毕.

记L(A),R(A),S(A)分别为End(A)的由L(x1,x2),R(x,x2),S(x1,x2)张成的线性空间, 即

L(A)=〈L(x1,x2)|∀x1,x2∈A〉,R(A)=〈R(x,x2)|∀x1,x2∈A〉,

S(A)=〈S(x1,x2)|∀x1,x2∈A〉,T(A)=L(A)+R(A).

定理5设A是半结合3-代数, 则T(A)是gl(A)的Abel子代数,L(A),R(A)为T(A)的理想.

证明: 由式(1),(2), 对任意xi∈A(1≤i≤5), 有

再由式(3), 有

所以[L(A),T(A)]=[R(A),T(A)]=0, [T(A),T(A)]=0. 结论得证.

定理6设A是半结合3-代数, 则下列结论成立:

1) 对∀x1,x2∈A,S(x1,x2)∈DerA;

2)S(A)是DerA的理想, 且[S(A),S(A)]=0,S(A)称为A的内导子李代数.

证明： 对∀x1,x2,x,y,z∈A, 由式(6),(7)，有

S(x1,x2){x,y,z}={x1,{x2,x,y},z}+{x1,{x,y,z},x2},

所以,

S(x1,x2){x,y,z}={S(x1,x2)(x),y,z}+{x,S(x1,x2)(y),z}+{x,y,S(x1,x2)(z)}.

结论1)得证. 对任意S(x1,x2)∈S(A),D∈DerA,x∈A, 因为

[S(x1,x2),D](x)=S(x1,x2)D(x)-DS(x1,x2)(x)=(S{x1,D(x2)}-S{D(x1),x2})(x),

所以[S(A),DerA]⊆S(A). 由定理4, 有

[S(A),S(A)]=[L(A)-R(A),L(A)-R(A)]=0,

结论2)得证.

2.2 半结合3-代数的型心

定义5设A是半结合3-代数, 则

Γ(A)={φ∈End(A)|φ{x1,x2,x3}={φ(x1),x2,x3}={x1,x2,φ(x3)}, ∀x1,x2,x3∈A}

称为A的型心. 由式(1), 对任意φ∈End(A),φ∈Γ(A) 当且仅当

φ{x1,x2,x3}={φ(x1),x2,x3}={x1,φ(x2),x3}={x1,x2,φ(x3)}, ∀x1,x2,x3∈A.

定理7设A是半结合3-代数, 则下列结论成立:

1)Γ(A)是一般线性李代数gl(A)的子代数;

2) 对任意φ∈Γ(A), 如果φ(A)⊆Z(A),φ(A1)=0, 则φ是中心导子;

3) 对任意φ∈Γ(A),D∈DerA, 则φD∈DerA;

4) DercA=Γ(A)∩DerA.

证明: 对任意φ1,φ2∈Γ(A),x1,x2,x3∈A, 由定义可知

[φ1,φ2]{x1,x2,x3}=(φ1φ2-φ2φ1){x1,x2,x3}={[φ1,φ2](x1),x2,x3},

[φ1,φ2]{x1,x2,x3}=(φ1φ2-φ2φ1){x1,x2,x3}={x1,x2,[φ1,φ2](x3)}.

所以 [φ1,φ2]∈gl(A). 结论1)成立.

对任意φ∈Γ(A), 如果φ(A)⊆Z(A),φ(A1)=0, 则由定义5和式(5)可知φ∈DerA. 结论2)成立.

对任意φ∈Γ(A),D∈DerA和x1,x2,x3∈A, 因为

所以φD∈DerA. 结论3)成立.

对任意φ∈Γ(A)∩DerA, 由定义5和式(5)知, 对任意x1,x2,x3∈A, 有

φ{x1,x2,x3}={φ(x1),x2,x3}+{x1,φ(x2),x3}+{x1,x2,φ(x3)}=3φ{x1,x2,x3},

所以φ(A1)=0. 再由

φ{x1,x2,x3}={φ(x1),x2,x3}={x1,x2,φ(x3)}=0,φ(A)⊆Z(A)

成立, 可得Γ(A)∩Der(A)⊆Derc(A). 如果φ∈DercA, 则φ∈Γ(A), 蕴含DercA=Γ(A)∩DerA. 结论4)成立.

定理8设A是半结合3-代数, 则对任意D∈Der(A),φ∈Γ(A), 下列结论成立:

1) [D,φ]⊆Γ(A);

2)Dφ∈Γ(A)的充要条件是φD∈DercA.

3)Dφ∈DerA的充要条件是[D,φ]∈DercA.

证明: 对任意D∈DerA,φ∈Γ(A)及x1,x2,x3∈A, 由

Dφ{x1,x2,x3}={Dφ(x1),x2,x3}+φD{x1,x2,x3}-{φD(x1),x2,x3},

Dφ{x1,x2,x3}=φD{x1,x2,x3}-{x1,x2,φD(x3)}+{x1,x2,Dφ(x3)},

有

(Dφ-φD){x1,x2,x3}={(Dφ-φD)(x1),x2,x3},

(Dφ-φD){x1,x2,x3}={x1,x2,(Dφ-φD)(x3)}.

所以[D,φ]∈Γ(A). 结论1)成立.

由定理6知,φD∈DerA. 如果Dφ∈Γ(A), 则由[D,φ]∈Γ(A), 有φD∈Γ(A). 所以φD∈DerA∩Γ(A). 反之, 如果φD∈Γ(A), 则由[D,φ]∈Γ(A)和Dφ∈Γ(A)可得结论2). 由结论1)和结论2)直接可得结论3). 证毕.