镰刀型曲线的显式表达式—— 作为曲线收缩流解

张文俊

(温州大学数理学院，浙江温州 325035)

1 曲线收缩流的两类特殊解

曲线收缩流方程为[1]：

其中k(u,t)是曲线的曲率，N(u,t)是曲线F(u,t)的单位内法向量．它是平均曲率流和高斯曲率流的典例，与之相关的文献如[2]和[3]等．此方程看似简单，但能写出其显式解的却很少，经典文献可参考[4]．

引理1F(s)是直线等价于曲率k恒等于0[5]．

定理1 直线方程是曲线收缩流方程（1）的解．

证明：直线的几何形状不随时间的变化而变化（即直线的方程不依赖于时间），又由引理1可知，直线的曲率恒为零，不难验证直线是方程（1）的解．

引理2F(u)是半径为a的圆等价于曲率k恒等于常数．

证明：不妨设F(u,t)=(a(t)cosu,a(t)sinu)，由于，可得单位切向量T=(−sinu,cosu)，单位法向量由单位切向量逆时针旋转得到[6]，即：

由引理2可得F(u,t)=(a(t)cosu,a(t)sinu)的曲率，即有方程

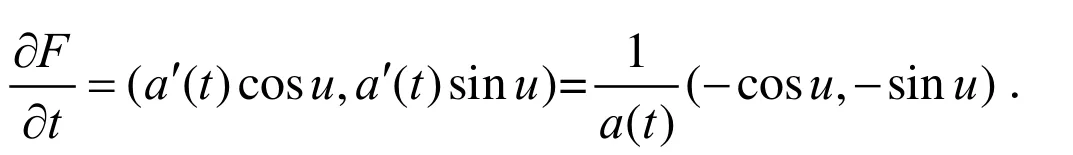
2 镰刀型曲线和曲线收缩流

以下我们考虑镰刀型曲线：

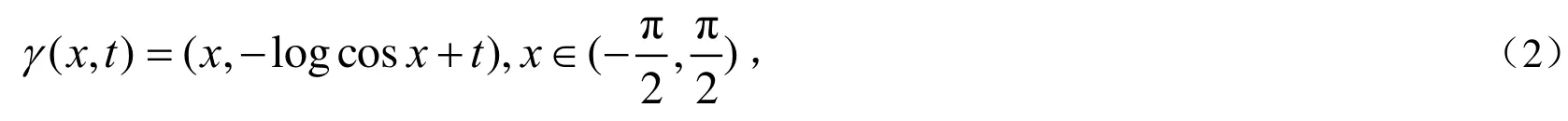
在下述意义下亦即方程（1）的显式解．

引理3 令向量T和向量N分别是镰刀型曲线γ(x,t)的单位切向量和单位内法向量，其中γ(x,t)满足：

可得k=cosx．联立方程（5）和（4）可得：．

注意到方程（2）和（1）相差一项切向量，因发展曲线切向量上的分量不影响其在发展过程中的几何形状，故我们可采用变量代换的方法来忽略此项．在曲线流奇点研究中，镰刀型曲线发挥着极其重要的作用，写出其作为方程（1）的解的显式表达有必要且具有价值．

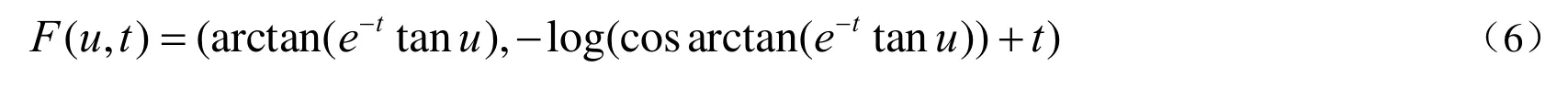
定理3 镰刀型曲线满足曲线收缩流方程（1），对任意的t∈(−∞,+∞)．

证明：为证镰刀型曲线为最初曲线收缩流（1）的解，引入明确的参数表示，令x=φt(u)且F(u,t)=γ(φt(u),t)，则有：

在方程（7）中，我们把u当作常量，然后解下述带有初值的常微分方程：

在方程（8）中，左右两边同时对t进行积分可得：

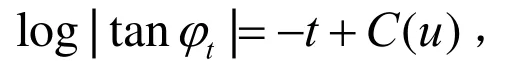
其中C(u)是关于u的函数且依赖于初值，令φ0=u，则有C(u)=log|tanu|，并且log|tanφt|=log(e−t|tanu|)，最后我们得到方程（8）的解：

3 镰刀型曲线的Frenet标架

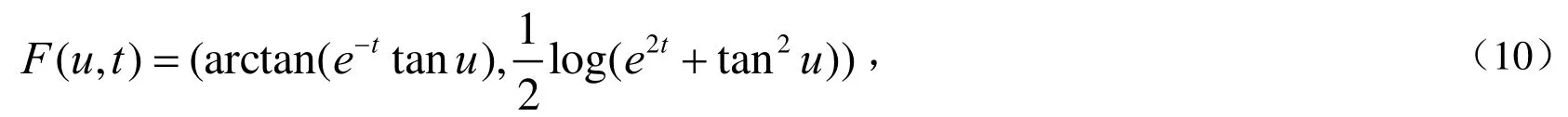
这里u∈(−∞,+∞)，并且t∈R．任意给定的Frenet标架不依赖于其参数的表达，方程（2），（6），（10）参数化的镰刀型曲线的Frenet标架相同．

则Ft(u)的弧长微分可写成如下形式：

并且Ft(u)的单位切向量和单位法向量分别为：

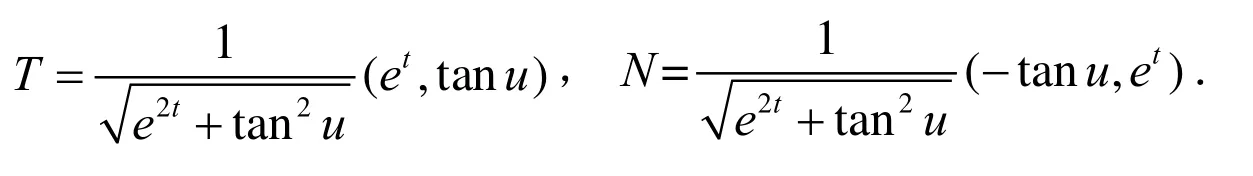
通过方程（11）可以得知，当u固定（u为一常数）时，可以得到镰刀型曲线曲率的极限，即．