不可压磁流体方程组的一个正则性准则

蒲青秀，郭正光

(温州大学数理学院，浙江温州 325035)

法拉第首次提出磁流体力学问题是在19世纪，他的想法是，利用海水切割地球的磁场产生电动势，然后测量泰晤士河两岸间的电位差，据此测出流速，不过因为河水电阻过大，地球磁场较弱和当时的测量技术差，没有达到测量的目的．一百多年后，哈特曼借鉴法拉第的方法，对另一种流体水银在磁场中的流动进行了一些定量的实验，并根据这些实验，成功地提出粘性不可压缩磁流体力学流动的理论计算方法．

磁流体力学（Magnetohydrodynamics，MHD）是流体力学的一个重要分支，是瑞典物理学家阿尔文创立的，阿尔文因此获得1970年的诺贝尔物理学奖．磁流体力学是研究流体的速度场和磁场之间互相作用的一门学科，在研究此类问题时要考虑两个方面，首先是磁场对流体的运动起什么作用，其次是流体运动对电磁场产生什么影响．磁流体力学理论应用十分广泛，例如，宇宙中恒星和星际气体都是等离子体，而且还有磁场，所以磁流体力学在天体物理中有不少应用．MHD方程组是磁流体力学的基本方程组，因此对MHD方程组的研究有着重要的理论意义和应用背景.

本文考虑的三维不可压磁流体方程组形式如下：

其中u=(u1(x,t),u2(x,t),u3(x,t))，b=(b1(x,t),b2(x,t),b3(x,t))，p=p(x,t)分别是未知的速度场、磁场和压力，u0(x)和b0(x)是给定的初始条件，当b=0时，就得到了Navier-Stokes方程，本文中很多思想来自Navier-Stokes方程．接下来简单介绍MHD方程的一些研究结果．

在文献[1]和[2]中，作者根据Navier-Stokes方程组的正则性准则，建立了仅依赖速度的Serrin-type正则性准则，即如果

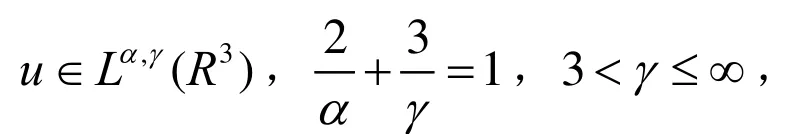
或

则方程组（1）的弱解在R3×(0,T)上是光滑的．

在柱坐标下，文献[3]证明了当b=bθ eθ时，如果

则方程组（1）的轴对称弱解是光滑的．

本文在文献[3]的基础上进一步研究MHD方程的轴对称弱解的条件正则性问题．

1 准备知识

引理1[4]设u∈W1,P且divu=0，w=curlu，则，对任意p∈(1,∞)成立，其中Cp只依赖于p．

引理2[5]若u∈W1,P，且divu=0为一个轴对称弱解，则，，其中Cp只依赖于p．

引理3[6]设，如果，令，如果p∈(3,∞)，令θ=∞，则存在一常数C使得对任意，，有：

在文献[3]中，作者在空间LP(0,T;Lq(R3))中考虑wθ进而得到弱解的正则性．根据这个思想，我们将空间扩大到中进一步来考虑其轴对称解．轴对称解的形式为：

其中，ur，uθ，uz分别表示速度场在r，θ，z方向上的分量，br，bθ，bz分别表示磁场在r，θ，z方向上的分量，由轴对称性，这些分量与θ无关．为研究方便，本文特假定br=bz=0，这里er=(sinθ,cosθ,0)，er=(−cosθ,sinθ,0)，er=(0,0,1)为柱坐标系下的一组规范正交基．得到如下定理．

2 定理及其证明

定理1 若(u,b)是MHD方程组（1）对应初始条件的全局轴对称弱解，且wθ满足：

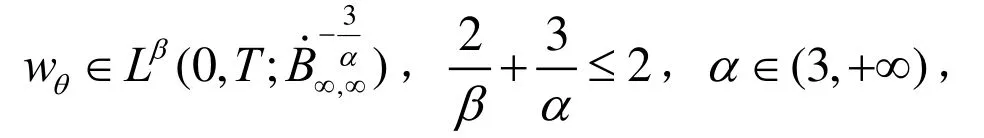
则(u,b)在上光滑．

通过基本的计算，方程组（1）可转化变成：

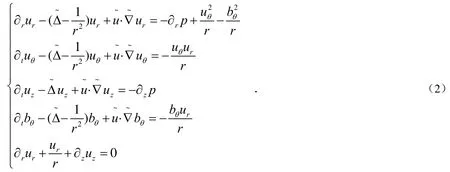
进一步得到如下的方程组：

将方程（3）的每个等式分别乘上wr,wθ,wz,j r,jz，并在R3上积分，有：

结合引理1，引理2，引理3有：

类似地有：

将F重新整理成：．最后对VI做出如下的估计：

将以上的这些项加起来并用Gronwall不等式可得：

3 结 论

本文定理1考虑的MHD方程组的轴对称解问题，是对文献[3]中定理的扩展，即由空间到的转化．本文关于轴对称解中的磁场只考虑了在θ方向上的，另外两分量上的则没有考虑，这也是我们以后要进一步研究的问题．