如何正确运用Z检验——两Poisson均值比较一般差异性Z检验及SAS实现

胡良平

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在自然界中，有一系列看起来彼此互不相干的随机变量，它们却遵从同一种分布规律。例如在单位空间中某些野生动物或昆虫数；在一定人群中某种患病率很低的非传染性疾病的患病数或死亡数等，这些“稀有事件”的发生次数常遵从一种被称为“Poisson分布”的概率分布。本文将简要介绍与该分布有关的主要内容，并结合精神卫生领域中的实例，介绍Poisson分布的具体应用方法以及基于SAS实现数据分析的技巧。

1 Poisson分布简介

1.1 Poisson分布

Poisson分布规律是由法国数学家Simeon Denis Poisson于1837年发现，故称为Poisson分布［1-3］。

1.2 Poisson分布的适用场合

Poisson分布常用于描述单位时间内或指定范围（平面或空间）内罕见“质点”总数的随机分布规律，常用于下列医学研究场合：①研究细菌、血细胞等单位面积（容积）内计数的分布；②人群中某些发病率很低的传染病的患病人数或死亡人数的分布；③人群中某些恶性肿瘤的患病人数或死亡人数的分布；④放射医学中放射性核素计数的分布；⑤某些疾病的地区或家族聚集性家庭数的分布；⑥癫痫患者治疗出院后在未来一年内癫痫发作次数的分布等。诸如此类“稀有事件”发生次数的分布规律的研究都可应用Poisson分布。

1.3 Poisson分布的定义

若离散型随机变量X的取值为非负整数，且相应的概率函数［4］为：

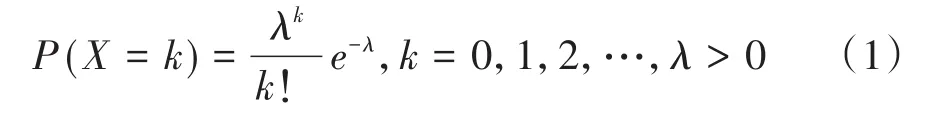
则称随机变量X服从Poisson分布，记作X～P(λ)。其中，λ为服从Poisson分布的随机变量X的均值，同时也是其方差。

1.4 Poisson分布的性质

Poisson分布具有很多优良的数学性质，包括：该分布的均值等于其方差；该分布具有可加性（即多个服从Poisson分布的随机变量之和仍然服从Poisson分布）；当其均值趋向无穷大时，分布趋向于标准正态分布。因篇幅所限，其他性质从略。

2 两Poisson均值比较的要领及SAS实现

2.1 问题与数据结构

【例1】文献［5］的目的是探讨卒中类型、卒中部位与卒中后癫痫的多因素关系，为卒中后癫痫的防治提供参考。以1 804例卒中患者为研究对象，收集其性别、年龄、卒中类型、卒中部位、卒中后癫痫发生的时间等资料，根据卒中后是否发生癫痫，将患者分为卒中后无癫痫组（n=1 487）和卒中后癫痫组（n=317），分析卒中后癫痫发作的危险因素。本例以文献［5］中卒中后出现癫痫的317例患者为研究对象，其中，早发性癫痫为141例，迟发性癫痫为176例。试探索卒中后早发性癫痫人数是否一定低于迟发性癫痫人数。

【例2】已知文献［5］中卒中后早发性癫痫患者共有141例，其中，男性98例，女性43例。试探索卒中后早发性癫痫患者中男性人数是否一定高于女性人数。

【例3】已知文献［5］中卒中类型为“额叶、颞叶”的患者卒中后出现癫痫的患者共有38例，其中，早发性癫痫为24例，迟发性癫痫为14例。试探索卒中后早发性癫痫人数与迟发性癫痫人数之间的差别是否具有统计学意义。

2.2 两Poisson均值比较的四要素

2.2.1 四要素之简介

在进行两Poisson均值的比较时，涉及到下列四个要素，即“检验假设（包括H0和H1）”“前提条件”“Z检验统计量”和“拒绝域”。由于这四个方面存在着密切的联系，需将它们合并在一起进行论述。

2.2.2 四要素之概述

两Poisson均值比较的四要素可以概括为下面的表格［6］，见表1。

表1 两Poisson均值比较的四要素

表1中的式（2）～式（5）如下：

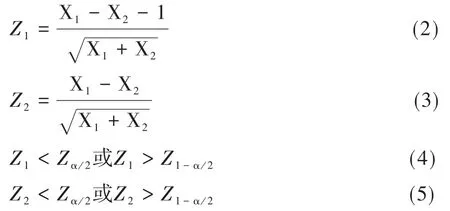
式（2）和式（3）中定义的“检验统计量（随机变量）”服从标准正态分布。

2.2.3 分析方法的合理选择

根据例1中已知的条件，可假定患癫痫病的人数近似服从Poisson分布。且因X1=141＜X2=176，希望得出它们对应的总体均值“λ1＜λ2”（属于备择假设）的结论，故本例属于“下单侧检验”问题。

根据例2中已知的条件，可假定患癫痫病的人数近似服从Poisson分布。且因X1=98＞X2=43，希望得出它们对应的总体均值“λ1＞λ2”（属于备择假设）的结论，故本例属于“上单侧检验”问题。

根据例3中已知的条件，可假定患癫痫病的人数近似服从Poisson分布；进一步还假定早发性癫痫人数与迟发性癫痫人数对应的总体均值不等（属于备择假设）的结论，故本例属于“双侧检验”问题。

2.3 两Poisson均值比较的SAS实现

SAS程序如下：

【程序说明】前7行是注释语句（即用“*”开头），第8和第9行为例1的数据，即现在是计算例1中的数据。若希望计算例2中的数据，就需要用第3和第4行替换第8和第9行（应删除开头的“*”）；若希望计算例3中的数据，就需要用第5和第6行替换第8和第9行（应删除开头的“*”）。

【SAS主要输出结果及解释】

以上为例1的输出结果，因例1属于“下单侧检验问题”。下单侧检验结果的判定：若z＜za，则接受（H1：λ1＜λ2）；否则，就接受（H0：λ1≥λ2）；PL为下单侧概率。又因z=-1.96580＜-1.64485，故P=0.024661＜0.05，应拒绝零假设，而接受备择假设，即可以认为，在总体上，卒中后早发性癫痫人数少于迟发性癫痫人数。

以上为例2的输出结果，因例2属于“上单侧检验问题”。上单侧检验结果的判定：若z＞z1_a，则接受（H1：λ1＞λ2）；否则，就接受（H0：λ1≤λ2）；PU为上单侧概率。又因z=4.63184＞1.64485，故P=0.000001812＜0.05，应拒绝零假设，而接受备择假设，即可以认为，在总体上，卒中后早发性癫痫患者中男性人数多于女性人数。

以上为例3的输出结果，因例3属于“双侧检验问题”。双侧检验结果的判定：若z＜zha或z＞z1_ha，则接受（H1：λ1≠λ2）；否则，就接受（H0：λ1=λ2）；PT为双侧概率。又因，故P=0.10476＞0.05，应接受零假设，即可以认为，在总体上，卒中后早发性癫痫人数与迟发性癫痫人数相等。

3 讨论与小结

3.1 讨论

服从Poisson分布的随机变量属于离散型随机变量，其取值为0、1、2等，这样的随机变量及其取值一同被称为“计数资料”。本文通过将两个服从Poisson分布的“计数数据”直接代入公式计算，其中每一个计数数据都被视为特定条件下的一个“均值”，就可获得检验统计量的数值，这样的“计数数据”与“家庭人口数”“脉搏次数/分钟”等的“计数资料”似乎是完全一样的，但当没有理由认为后者是服从Poisson分布时，是不能仅依据两个“计数数据”就进行假设检验的，而需要将它们视为“计量资料”，在求得“平均值”或“平均秩”后，再采取相应的统计分析方法进行假设检验。

3.2 小结

本文结合3个实例，介绍了两Poisson均值比较的三种Z检验及SAS实现。在统计学上，一般按“备择假设”所决定的“方向（大、小顺序）”来确定“上单侧检验”“下单侧检验”或“双侧检验”。当备择假设为“A＜B”时，就是“下单侧检验（拒绝域位于概率分布曲线下的左侧尾端）”；当备择假设为“A＞B”时，就是“上单侧检验（拒绝域位于概率分布曲线下的右侧尾端）”；当备择假设为“A≠B”时，就是“双侧检验（对关于坐标原点对称分布而言，拒绝域位于概率分布曲线下的左、右两尾端，例如标准正态分布和t分布。而对仅取零和正值的非对称分布而言，拒绝域位于概率分布曲线下的左侧或右侧，例如Poisson分布、F分布、χ2分布等）。