基于鲁棒反馈线性化的联合收获机割台高度控制策略

庄肖波 李耀明

(江苏大学现代农业装备与技术教育部重点实验室， 镇江 212013)

0 引言

联合收获机的使用大幅提高了谷物收获效率、减轻了劳动强度，并显著降低了农业生产对劳动力的需求。随着联合收获机的高速化、智能化发展，割台的自化控制得到了广泛研究[1-3]。

割台高度控制最早出现在20世纪五六十年代[4]，早期涉及开关控制[5]，直到20世纪末，开关控制仍被认为是最先进的[6]。比例控制被引入到PID控制器[7-9]，LQR[10]和LQG[11-12]等二次型控制方法也得到大量研究。文献[13]分析了联合收获机割台高度控制中机械设备的基本限制因素，为了克服这些限制因素，文献[14-15]提出了机械参数与控制器同时设计的方法。反馈线性化是一种控制设计策略，可以用来设计非线性系统控制器[16]。尽管反馈线性化具有良好的跟踪性能，但其主要局限性在于鲁棒性较差，因为反馈线性化过程需使用精确模型来消除动力学中的非线性。文献[17-18]使用Lyapunov考虑参数的不确定性，增强反馈线性化的鲁棒性，但这种方法需估计不确定性的界。另一种鲁棒反馈线性化方法是滑模控制[19-20]。鲁棒反馈线性化控制非常适合于在工作点不能线性化的非线性系统。文献[21]提出了集成鲁棒优化设计(Integrated robust optimal design，IROD)，该方法比H∞[22]方法具有更好的跟踪性能，但目前研究主要集中在机械系统上，对液压控制系统的研究较少。为从液压执行器中获得期望的输出，需对液压系统动力学特性进行理想化，需设计一个单独的液压控制器。为使系统更具鲁棒性，可通过设计联合收获机割台高度液压控制系统的鲁棒反馈线性化控制器加以实现。

本文基于割台结构和动力学分析建立系统数学模型，选取正弦角度的近似约简条件，将多变量的复杂非线性系统转换为典型的非线性系统；分析传统的反馈线性化控制，在集成鲁棒优化设计(IROD)控制器基础上提出鲁棒反馈线性化(RFL)，通过构建灵敏度方程、选取增益来稳定系统；选取液压控制机构，以控制液压输出的电流为控制系统的输出来设计控制器。最后，通过仿真实验和实物实验验证控制方法的有效性。

1 系统数学模型

建立割台动力学模型如图1所示。以球铰O′和切割器的两端CD建立割台平面。割台ABCD在O′处通过球铰与机架铰接，两侧液压缸MP和NQ提供动力FM和FN。设割台绕AB的转角为θ，CD处安装切割器，使用传感器采集其两端离地面高度z1和z2。

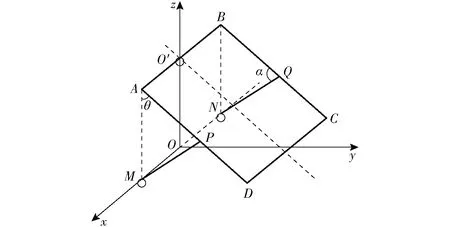
图1 割台动力学模型Fig.1 Dynamic model of header

对图1所示模型进行动力学分析。考虑割台绕AB的俯仰运动，得到割台yz平面上的旋转动力学方程为

(1)

其中

(2)

式中k——俯仰转动的等效阻尼系数

J1——割台俯仰的转动惯量

m——割台质量

l——点A与点D间长度

l1——点A与点P间长度

α——油缸轴与割台平面的夹角

h——点A与点M间高度

从传感器获得点C、D离地面高度，并满足

(3)

(4)

式中z1——点C离地面高度

z2——点D离地面高度

t——割台宽度，即点C、D间的距离

为简化运算，由于割台实际工作时转角的调整值Δθ较小，以sinΔθ≈Δθ的近似条件进行线性化操作。将式(2)代入式(1)，再对式(1)、(3)、(4)进行线性化，得

(5)

(6)

(7)

式中αs——割台处于静态平衡状态时的α

θs——割台处于静态平衡状态时的θ

P——系数，为θs的函数

Δz1——点C离地面高度变化量

Δz2——点D离地面高度变化量

ΔFM——液压缸MP动力变化量

ΔFN——液压缸NQ动力变化量

FMs——液压缸MP处于静态平衡时的FM

FNs——液压缸NQ处于静态平衡时的FN

综合式(5)～(7)，可建立割台模型为

(8)

可得到状态空间方程为

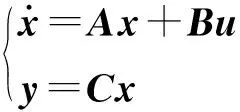
(9)

其中

(10)

根据式(9)、(10)可得到方程

(11)

式中x——状态矢量u——矢量输入

y——数量输出

由此得到一个典型的非线性系统，可进一步转换成输入输出的反馈线性化系统。

2 传统反馈线性化控制

在很多系统中，尤其是液压系统，为一个不可控的仿射系统，将式(11)表示为更一般的形式

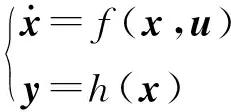
(12)

(13)

其中

(14)

则得到标准输入输出，进一步线性化设计可用于扩展系统。并根据时间t离散化输出y，可得

(15)

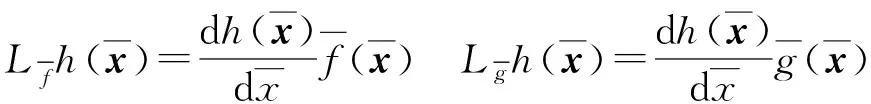
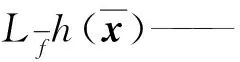
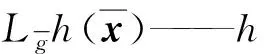
(16)

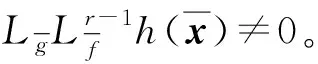
(17)

由式(17)可得，线性化反馈控制映射计算式为

(18)

v可以参考信号R来选择，计算式为

(19)

通过选择增益K1、K2、…、Kr来稳定系统。理论上，增益越高，跟踪性能越好，但增益过高会导致高频振荡或抖动，特别是在导数项较高的情况下，会导致不稳定。

3 鲁棒反馈线性化控制

反馈线性化控制器本质上缺乏鲁棒性，因式(18)计算的控制输入高度依赖于系统的识别准确度。如果系统方程中有不确定的参数，可能会影响反馈线性化控制器的稳定性。为了反馈线性化控制器选定的不确定参数具有更强的鲁棒性，可构建系统的灵敏度动力学方程和调整控制输入，以尽量减少不确定参数的影响。

考虑具有不确定参数的线性系统

(20)

其中，b∈R是一个未知参数，也可以推广到b是多个未知参数向量的系统，本文将b假定为标量。式(20)的灵敏度动力学可计算为

(21)

式中xb——灵敏度状态向量，xb∈Rn

yb——输出灵敏度

下标b表示未知参数关于b的全导数，可以表达为

(22)

式(22)意味着控制输入w与未知参数b无关。在反馈控制的情况下不成立，因为输出用于控制输入计算，所以w间接依赖于参数。因此，还必须考虑w相对于b的导数，并要求将链式规则应用于式(19)的第2项。随系统方程增加的灵敏度动力学为

(23)

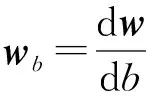
鲁棒反馈控制输入wb是为了使系统灵敏度最小化，从而使系统更具鲁棒性。对于式(23)的系统，转换输入的灵敏度vb计算式为

(24)

将链式规则应用于式(24)中的第2项，灵敏度变成

(25)

其中

(26)

下标b遵循式(22)的约定。

因为所需灵敏度为0，所以选择vb为

(27)

选择增益Kb1、Kb2、…、Kb3来稳定灵敏度。与标称系统一样，理论上较高的增益会得到更好的跟踪性能，但过高的增益会导致高频振荡或抖动，特别是高阶导数。鲁棒反馈线性化控制系统的框图如图2所示。

图2 一般控制非仿射系统的鲁棒反馈线性化控制结构Fig.2 Robust feedback linearization control structure for a general control non-affine system

4 基于鲁棒反馈线性化的控制器设计

割台高度控制由两个单独作用的液压机构驱动，每个由两个比例双向提升阀控制。一个阀控制从高压泵管路流入油缸的流量，而另一个阀控制流出油缸的流量。选择HydraForce公司的SP16-20型阀和SP10-20型阀。从HydraForce官网获得SP16-20型阀和SP10-20型阀性能流量曲线，并通过Matlab获得性能流量为

q=a1i+a2iΔp+a3i2+a4i2Δp

(28)

其中，可以用n维数组表示控制电流i，m维数组表示压差Δp，m×n维数组表示相应的流量q。a1～a4的拟合值如表1所示。

表1 提升阀多项式方程常数Tab.1 Poppet valve polynomial equation constants

单作用液压执行机构的运动方程为

(29)

式中X——活塞位置V——活塞速度

V0——活塞初始速度

β、As——系数p——活塞压力

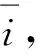
(30)

液压系统的输出是由液压缸提供的力，计算式为

F=pAs

(31)

从液压运动方程出发，建立割台高度液压系统的状态空间模型为

(32)

其中

(33)

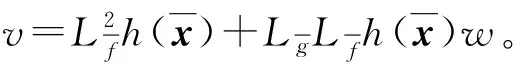
(34)

将期望力和实际力之间的误差最小化

(35)

根据式(35)和实验，选择增益为：K1=105和K2=103。

为了调整输入电流对不确定性的影响，使控制器更具鲁棒性，计算了对不确定参数的灵敏度。选取不确定参数为液压流体体积模量。为了计算灵敏度动态，根据式(22)，将等式(33)中的系统与β区分开来。为了使灵敏度最小，对增敏系统进行反馈线性化。得到wb最简单的方法是对式(34)直接关于β微分，然后求解wb可得

(36)

根据式(36)设计稳定灵敏度输出。系统选择的增益为：Kb1=4×106和Kb2=4×104。

5 实验

在Matlab的Simulink中建立了联合收获机割台提升系统的闭环控制系统。如图3所示，本文提出的鲁棒反馈线性化(RFL)方法与集成鲁棒优化设计(IROD)方法相结合，设计联合收获机割台高度自动控制控制器。其目标是联合收获机向前移动时，提高收割台对地形的跟踪性能，同时优化控制输入，使其对不确定参数具有鲁棒性。机械系统的控制器基于IROD方法。鲁棒反馈线性化(RFL)系统框图如图4所示。

图3 收获机割台高度控制的仿真系统框图Fig.3 Block diagram of simulation system for header height control of harvester

图4 RFL控制器仿真框图Fig.4 RFL controller simulation block diagram

该系统包括文献[16]中设计的集成鲁棒优化设计(IROD)控制器、本文设计的鲁棒反馈线性化(RFL)控制器以及使用SimScape环境的液压和机械设备模型，将其建模为振幅和频率变化的正弦输入，由于正弦频率是车辆行驶速度和地形剖面的函数，因此将分别指定地形周期、长度单位和车辆行驶速度。

为了测试设计的控制系统性能，将其与PID控制器进行了比较。对于PID系统，IROD/RFL控制器都被一个单独的PID控制器所代替，如图5所示。增益使用Matlab控制设计工具箱进行调整，工具箱自动线性化对象，并基于标准阶跃输入选择增益，以实现最佳参考跟踪。然后，在与模拟测试相同的条件下，通过模拟手动调整增益。最终确定为KP=1.3，KI=1.5，KD=0.5。在该应用中，通常只使用PI控制器实现稳健目的，但需在测试的基准测试条件下为PID控制器提供最佳的参考跟踪。

图5 割台高度PID系统控制框图Fig.5 PID control structure system of header height

在相同条件下对PID和IROD/RFL控制器进行了仿真。行驶速度为0～10 km/h、地形正弦振幅为0.5～1.0 m、地形周期为16～36 m，将仿真时间设为30 s。

图6 IROD/RFL和PID控制器不同行驶速度和地形振幅下的割台高度跟踪最大误差Fig.6 Maximum header height tracking error of IROD/RFL and PID controllers at various travel speeds and terrain amplitudes

由图6可知，与PID控制器相比，使用IROD/RFL控制器的收割台高度跟踪明显更好，表明IROD/RFL控制器的性能更好。在相同的地面条件下，IROD/RFL控制器在5.0 km/h时的性能优于PID在2.0 km/h时的性能。

在图7所示的割台高度控制实验场地上，地形振幅为0.3 m。实验采用某联合收获机，相关参数如表2所示。分别以2、4、8 km/h的速度在同一起伏路段上行进20 m，每隔0.1 m对割台高度和地面高度数据进行采集。

图7 割台高度控制实验场地Fig.7 Experimental site of header height control

实验调整割台初始高度为0.2 m，设置控制的目标高度为0.1 m。PID和IROD/RFL的控制器效果如图8、9所示。

表2 某联合收获机割台状态参数Tab.2 Parameters of header at equilibrium

从图8、9可得，随着行驶速度的增大，PID和IROD/RFL的高度误差也在增大，并且前者的误差增加的幅度明显大于后者。6组实验数据高度误差的均方根如表3所示。由表3可知，同一行驶速度下，IROD/RFL控制的高度误差小于PID控制时的高度误差；并且，随便行驶速度的增大，IROD/RFL控制的高度误差变化也明显小于PID的误差。

图8 PID控制系统高度误差曲线Fig.8 Height error curve based on IROD/RFL

图9 IROD/RFL控制系统高度误差曲线Fig.9 Height error curves based on IROD/RFL control

表3 PID控制器和IROD/RFL控制器高度误差均方根Tab.3 RMS of height error of PID and IROD/RFL

6 结论

(1)传统的反馈线性化技术不适用于不可控的仿射系统。通过重新定义状态和状态方程，可将不可控的原始系统转换为扩展的可控仿射系统。

(2)控制系统输入依赖于系统参数的准确度，使反馈线性化控制器鲁棒性较差。增加系统的灵敏度动力学和调整控制输入可使反馈线性化控制器对选定的不确定参数具有更强的鲁棒性。

(3)割台高度调节反馈由集成鲁棒优化设计决定最优控制力，利用鲁棒反馈线性化控制液压流量输出，能够有效提高系统的鲁棒性。

(4)随着行驶速度、地形振幅的增加，传统PID控制和IROD/RFL控制下的割台高度误差均随之增大；在相同仿真条件下IROD/RFL控制下的误差均小于传统PID控制下的误差。在不同行驶速度下，IROD/RFL控制的高度误差均小于PID控制的误差，并且误差受行驶速度增加的影响较小。本文提出的IROD/RFL的高度控制方法比基于传统PID高度控制具有明显的优势。