Geometrically Nonlinear Random Responses of Stiffened Plates Under Acoustic Pressure

，，，

1.College of Civil Engineering and Architecture，Hebei University，Baoding 071002，P.R.China；2.Department of Engineering Mechanics，Beijing University of Technology，Beijing 100124，P.R.China；3.Science and Technology on Reliability and Environment Engineering Laboratory，Beijing Institute of Structure and Environment Engineering，Beijing 100076，P.R.China

（Received 10 June 2020；revised 20 July 2020；accepted 1 September 2020）

Abstract:An algorithm integrating reduced order model（ROM），equivalent linearization（EL），and finite element method（FEM）is proposed to carry out geometrically nonlinear random vibration analysis of stiffened plates under acoustic pressure loading.Based on large deflection finite element formulation，the nonlinear equations of motion of stiffened plates are obtained.To reduce the computation，a reduced order model of the structures is established.Then the EL technique is incorporated into FE software NASTRAN by the direct matrix abstraction program（DMAP）.For the stiffened plates，a finite element model of beam and plate assembly is established，in which the nodes of beam elements are shared with shell elements，and the offset and section properties of the beam are set.The presented method can capture the root-mean-square（RMS）of the stress responses of shell and beam elements of stiffened plates，and analyze the stress distribution of the stiffened surface and the unstiffened surface，respectively.Finally，the statistical dynamic response results obtained by linear and EL methods are compared.It is shown that the proposed method can be used to analyze the geometrically nonlinear random responses of stiffened plates.The geometric nonlinearity plays an important role in the vibration response of stiffened plates，particularly at high acoustic pressure loading.

Key words：stiffened plate；acoustic loading；geometric nonlinearity；random vibration；equivalent linearization

0 Introduction

Stiffened plates and shells are common structural forms used in the aerospace industry［1］，owing to their many advantages over unstiffened plates，such as their very high stiffness to weight ratio.Stiffened panel usually consists of a basic structure and local reinforcement elements called stiffeners are added to improve the static and dynamic characteristics of the structure.The behavior of stiffened plate structures subjected to linear random vibrations under low levels of acoustic excitation is readily determined because approximate solutions of the equations of motion are readily obtained under these conditions.However，stiffened plates readily sustain large amplitude vibrations when subjected to excessive acoustic excitation.In this case，the structural stiffness employed in the equations of motion governing a plate is dependent upon the magnitude of deflection，making the equations of motion nonlinear，and difficult to solve.In addition，the structural discontinuity and anisotropy are induced by stiffeners.This unique characteristic makes the nonlinear random vibration response analyses much more complicated than those of the unstiffened plate.For these reasons，the equations of motion are far more complex in the case of nonlinear random vibrations，and obtaining approximate solutions in a computationally efficient manner is very difficult.Therefore，the development of theoretical models and computationally efficient approaches for obtaining reasonably accurate approximate solutions of nonlinear motion equations is essential for achieving a thorough understanding of the nonlinear random vibration response of stiffened plates under acoustic loads.

Numerous studies of the vibration characteristics of stiffened plates have been conducted using various theoretical models and solution approaches.Ma et al.［2］investigated the nonlinear forced vibration of the stiffened plates with four clamped edges based on the Lagrange equation and the energy principle.Chen et al.［3］investigated the strongly nonlinear free vibration of four edges simply supported stiffened plates with geometric imperfections.Cho et al.［4］dealt with numerical procedure for the vibration analysis of rectangular plates and stiffened panels subjected to point excitation force and enforced displacement at boundaries.Sheikh and Mukhopadhyay［5-6］investigated the geometric nonlinearity of stiffened plates by the spline finite strip method，and applied this method to analyze linear and nonlinear transient vibration of plates and stiffened plates.Mitra et al.［7］studied the influence of stiffener position，plate aspect ratio，and stiffener to plate thickness ratio on the large amplitude dynamic behavior.Qing et al.［8］developed a novel mathematical model for free vibration analysis of stiffened laminated plates by separate consideration of plate and stiffeners based on the semi-analytical solution of the statevector equation theory.Li et al.［9］proposed the Karhunen-Loeve expansion（KLE），finite element method（FEM），and boundary element method（BEM）（KLE/FEM/BEM）to carry out vibroacoustic analysis of stiffened panel under stationary and non-stationary random excitations.Dogan［10］used the Galerkin type approach to study the nonlinear vibration of clamped functionally graded material plates under random excitation，but it is difficult to apply this method to the systems with complex geometry and boundary conditions.

One of the most widely used approximation techniques for the random problem is the equivalent linearization（EL）that the nonlinearities in system are replaced by effective linear systems.The advantage of the EL method is that it can be combined with FEM and applied to nonlinear systems with complex geometry and boundary conditions.Robinson et al.［11］predicted the nonlinear random response of structures using an EL technique by means of the direct matrix abstraction program（DMAP）modifications in NASTRAN.While it is possible to perform an EL analysis in the physical degrees-of-freedom，it is desirable to transform the problem into modal coordinates to simplify the problem.

One approach for reducing the computational burden associated with solving ordinary differential equations is to reduce the order of the equations using the mode summation method.Here，a physical multiple degree of freedom system is translated into a modal system，which is convenient for analyzing its nonlinear random vibrations.The appropriate selection of modal basis vectors and the determination of nonlinear stiffness coefficients in the reduced-order equations are essential aspects of this approach.Rizzi and Przekop［12］investigated the effect of modal basis selection on geometric nonlinear response prediction using a reduced-order nonlinear modal simulation.Przekop et al.［13］examined three procedures for guiding the selection of an efficient modal basis in a nonlinear random response analysis.Kim et al.［14］developed nonlinear structural dynamic reduced-order models of beams and plates，and established their validity.Mignolet et al.［15］presented an extensive review of indirect methods for the construction of reduced-order models employed for the prediction of the vibration responses of geometrically nonlinear structures represented by finite element models.Parandvar and Farid［16］studied the large amplitude vibration of functionally graded material plates subjected to combined random pressure and thermal loadings using the finite element modal reduction method.Przekop and Rizzi［17］adopted a reduced-order method to investigate the geometrically nonlinear response of structures exposed to combined loadings，and investigated the effect of modal basis selection on the quality of the results obtained.

The numerical results for a thin simply-supported aluminum plate［18］are in good agreement with previously reported data in Refs.［19-20］，which confirms that the proposed method has reasonable precision and high efficiency.But the implement method is not applied to stiffened plate.It should be pointed out that Solution 106 cannot analyze the large deformation of the stiffened plate with offset and the nonlinear nodal forces cannot be obtained.So，the nonlinear nodal forces of the stiffened plate need to be solved in Solution 400.In this paper the implementation method proposed in Ref.［18］is improved，and then it is applied to stiffened plates.

This paper is organized as follows.In Section 1，the large deflection finite element formulations of stiffened plates are briefly introduced to establish the general nonlinear equations of motion.In Section 2，the EL method for geometrically nonlinear random vibration is introduced，and an improved implementation of the EL method is presented.In Section 3，a numerical example，including linear and geometrically nonlinear random vibration analyses of stiffened plates，is given.Finally，the main conclusions are summarized in Section 4.

1 Reduced Order Model of Geometrically Nonlinear Structures

The system mass，damping and stiffness matrices are generally obtained using a commercial finite element software.But the nonlinear stiffness which is related toΓT，is not available within a commercial finite element software.The equations of motion of a multiple degree-of-freedom，viscously damped geometrically nonlinear system can be written in the form

or in more general form，as

where the matricesM，CandKare the mass，proportional damping，and linear stiffness matrices，respectively.X(t)is the displacement response vector andP(t)the force excitation vector.The coefficientsK1andK2are the system first and second-order nonlinear stiffness coefficients.For the problems of interest，the nonlinear restoring force vectorΓcan be adequately represented by quadratic and cubic order terms inX.

Performing an EL analysis in the physical degrees-of-freedom is very difficult.To reduce the computational cost and time，a modal equation with reduced degrees-of-freedom is obtained by applying the modal coordinate transformation

to Eq.（2），a modal equation of motion can be written as

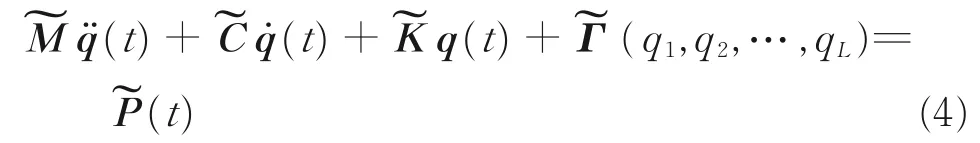
where

whereq1，q2，…，qLare the components ofq，andqis the vector of modal coordinates.ζris the viscous damping factors，ωrthe undamped natural frequencies，andΦgenerally the subset of the linear eigenvectors obtained from Eq.（2）withoutΓ.A normal modes analysis was performed to obtain the modal matrixes，from which modes with relatively high modal effective mass fraction were selected as the modal base vectors to reduce order of the equations of motion［21］.

The nonlinear restoring force components in modal space are replaced by the product of quadratic and cubic nonlinear modal displacements multiplied by unknown nonlinear modal stiffness coefficients.In the present paper，the assumed form of the nonlinearities will be cubic based upon previous studies of aircraft structural response［22］.Thus，it can be written as

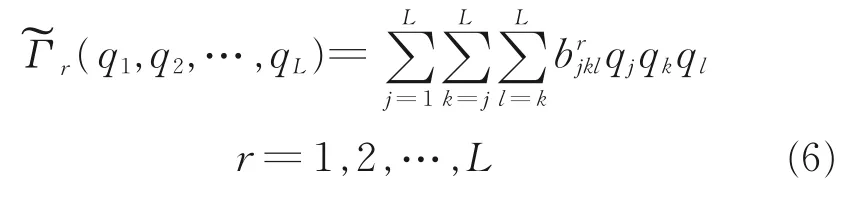
whereLis the number of modal base vectors.This form is sufficient for characterizing the type of nonlinearity of interest in this paper and facilitates the subsequent solution of the equivalent linear system.The particular displacement fields are given for a series of inverse linear and nonlinear static analysis to determine the coefficients.The total nodal forceFTmay be written in physical coordinates as

whereXcis a prescribed physical nodal displacement vector，andFLandFNLare the linear and nonlinear contributions to the total nodal force.FLis first obtained by prescribingXcin the linear static solution.FTis then obtained by prescribingXcin the nonlinear static solution which includes both the linear and nonlinear contributions.Note in linear analysis，assuming the displacements are small and the nonlinear terms are negligible，the nodal force vector isFL=KXc.Finally，the nonlinear contributionFNLis obtained by subtractingFLfromFT，or

One can begin by prescribing the displacement fields

whereφiis mode shape vector（eigenvector）.The nonlinear nodal force contributionsFNLare determined using Eq.（8）after solving the linear and nonlinear static solutions.These may be written in modal coordinates as

where the sought stiffness coefficientsare vectors of lengthL.Note that the other nonlinear terms do not appear in Eq.（10）sinceqj=0 forj≠1.Sinceq1is a known scalar，the coefficientsforr=1，2，…，Lcan be determined from the resulting system Eq.（10）ofLlinear equations.The remaining coefficientsfor(j=2，3，…，L)can be determined in an analogous manner.

A similar technique can be used to determine stiffness coefficients with two unequal lower indices，e.g.and.Coefficients of this type appear only if the number of retained eigenvectors is greater than or equal to two(L≥2).Prescribing the displacement fields

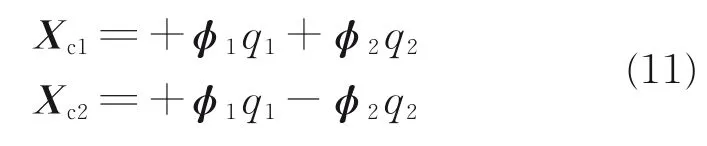
results in the following equations

The first equation of Eq.（12）plus or minus the second，results in

From Eq.（13），the coefficientsandmay be determined from the 2×Lsystem of equations.In this manner，all coefficients of the typeandforj，k=1，2，…，Lmay be found.For cases when the number of retained eigenvectors is greater than or equal to three(L≥3)，coefficients with three unequal lower indices，e.g.，may be determined by prescribing the displacement field

The resulting equation

contains one column of unknown coefficients.All coefficients of typecan be found in this manner.

The nonlinear stiffness coefficientsbjklin Eq.（6）were obtained using a Fortran computer code denoted as nonlinear stiffness evaluation（NLSE）.As a result，the implicit geometrically nonlinear equation of motion is represented as an explicit equivalent nonlinear equation of motion in modal coordinates.For a random loading，the solution of Eq.（4）with the nonlinear terms can be undertaken through numerical simulation or EL method.In this study the EL method is considered below.

2 Force Error Minimization of Equivalent Linearization Method for Random Loading

2.1 Theoretical foundation

Eq.（2）has no general solution when the excitation is random.An approximate solution can be obtained by using formation of an equivalent linear system

whereKeis the equivalent linear stiffness matrix.While it is possible to perform an EL analysis in the physical degrees of freedom，it is desirable to recast the problem in modal coordinates to simplify the problem.The equivalent linear analog of Eq.（4）may be found by applying Eq.（3）to Eq.（16）

where the modal equivalent linear stiffness matrixis given by

The traditional force-error minimization method of EL was adopted to seek the minimizing between the nonlinear force and the product of the modal equivalent linear stiffness and displacement response vector.The error in the approximate system is defined as

Since the error is a random function of time，the required condition is that the expectation of the mean square error be a minimum.This is expressed as

whereE[·]represents the expectation operator.Eq.（20）will be satisfied if

Using the fact that the matrixEis nonsingular，the matrixcan be determined

2.2 Iterative solution for modal equivalent linear stiffness matrix

where superscriptmis the iteration number.At the start of the first iterationis equal to zero.Assuming stationary excitation，a stationary response is sought precluding the need for initial conditions.Note that in modal coordinates，the order of these matrices is not large，so it is not difficult to calculate the frequency response matrixH(ω)at each frequency，i.e.

The introduction of the weightingsαandβis to aid in the convergence of the solution，with the condition thatα+β=1.As discussed in Ref.［18］，the weightingsαandβplayed a significant role in the convergence of the iterative procedure.The appropriate values forαandβwere adopted at various acoustic pressure levels.In this paper，two variable values ofαandβfor optimizing the convergence rate at high acoustic pressure levels are developed to decrease the step size and avoid divergence.

For the random vibration of linear system Eq.（26），the spectral density matrices of the modal responseSqqand excitationare related by

The spectral density matrix of the loading in physical degrees of freedom is the product of frequency response load vectorfmultiplied by its complex conjugate transpose

where the over-bar in Eqs.（28，30）indicates the complex conjugate，andfis the frequency response load vector.The zero-time-lag covariance matrix componentsE[qrqs]are calculated from the response spectral density matrix using the Wiener-Khinchin formula.For ther，scomponents，this is written as

Again，we note that the orders of matrices are not large in modal coordinates，so it is not difficult to calculate the covariance matrix by a simple numerical integration over frequency.After having done so，the updatedmay be calculated as a function of the response covariance matrix

Substitution of Eq.（6）into Eq.（33）yields

The iterations continue until the following convergence criterion is met

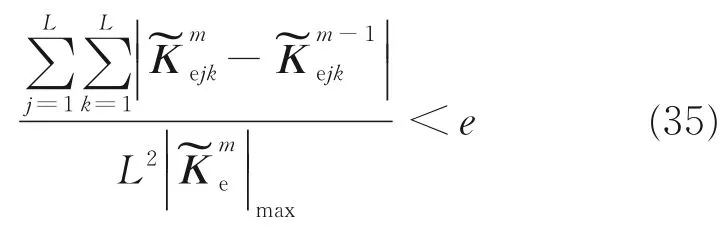
and RMS values are the square roots of the diagonal terms in Eq.（36）.Further post-processing to obtain power spectral densities of displacements，stresses，strains，etc.，may be performed by substituting the converged equivalent stiffness matrixinto Eq.（17）and solving in the usual linear fashion.

2.3 Implementation of equivalent linearization solution

The whole implementation process is referred to Ref.［18］.It should be noted that the process of determining the nonlinear stiffness coefficient of stiffened plate is different from that of flat plate.

The present computer codes NLSE which mentioned in Ref.［18］was verified to be valid in plane structure.However，the implement method is not applicable to the stiffened plate.The Solution 106，which is called in the method，cannot analyze the large deformation problem of the stiffened plate，and the nonlinear node-force of its finite element model cannot be obtained.In order to solve this problem，the Solution 400 should be called and the options of“large deformation and large strain”and“stiffness varies with deformation”should be selected in the parameter setting to obtain the nonlinear node-force of the finite element model of the stiffened plate［24］.Here，the improved NLSE is applied to stiffened plates.The nonlinear stiffness coefficients are determined by performing a series of inverse linear static（Solution 101）and nonlinear static（Solution 400）solutions using particular displacement fields as previously described.

In this paper，we treat the acoustic excitation as random pressure acting on the surface of the plate.It is taken as uniformly distributed and varies in time.Acoustic pressure RMS and spectral density value corresponding to different sound pressure levels from 106 to 160 dB are shown in Table 1.

Table 1 Acoustic pressure RMS and spectral density value corresponding to different sound pressure levels

3 Numerical Example

3.1 Finite element model of stiffened plate and nonlinear stiffness coefficient

We consider a simply-supported rectangular aluminum stiffened plate.The plates and beams of the stiffened plates structure are discretized into twodimensional plane elements and one-dimensional beam elements respectively for analysis.Beam and plate can share nodes and beam offset distance can be set.The stiffness matrices of the stiffened plates are composed by the addition of the respective plate and beam element stiffness matrices.The dimensions and material parameters of the plate are provided in Table 2.A NASTRAN model of the stiffened plate is built with a uniform 20×28 mesh composed of 560 CQUAD4 elements 48 beam elements and 609 nodes.The finite element model of the stiffened plate is shown in Fig.1（a），and the cross-sectional area of the beam is shown in Fig.1（b）.The beam，plane element and joint at central position of the stiffened plate are shown in Fig.2.The mode shape，frequency（f）and modal effective mass fraction（η）of metal stiffened plates are shown in Table 3.It can be seen that the modal effective mass fraction of symmetrical modes（1，5，7，11）is larger.

Table 2 Dimensions and material properties of stiffened plate

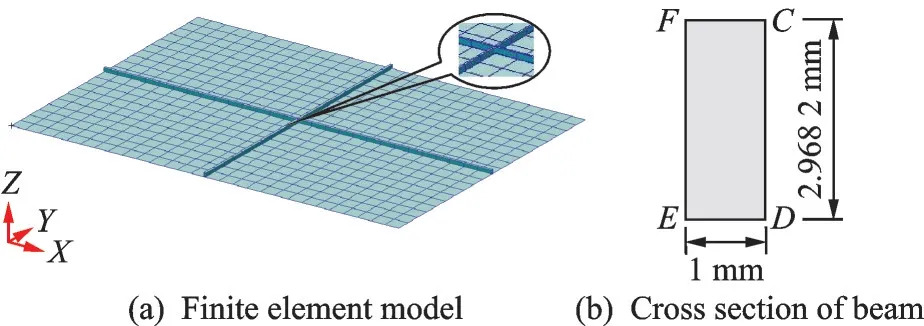
Fig.1 Stiffened plate model

Fig.2 Beam and shell elements at the center position

In this paper，the order of the equations of motion was reduced using the first two symmetric modes（mode 1 and mode 5）.

Accordingly，Eq.（34）can be written as

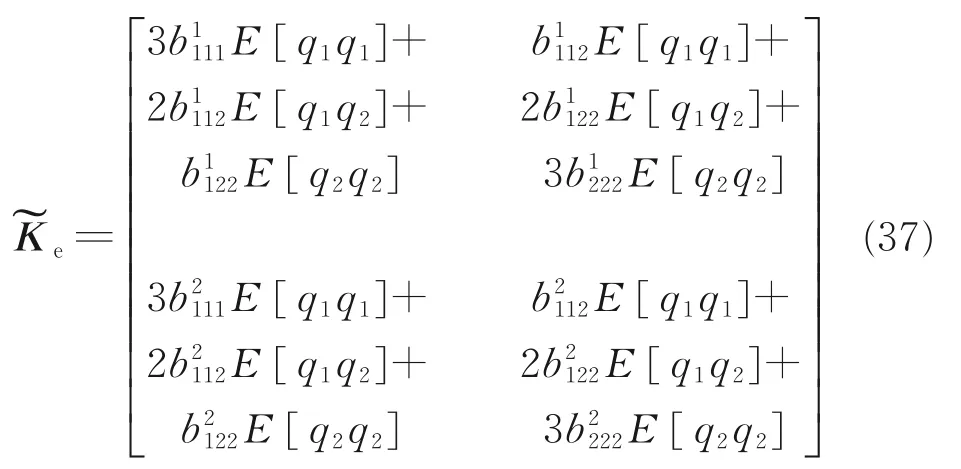
To ensure the symmetry of the matrixand through comparison of terms with like powers inqjandqk（and taking into account thatqjandqkcan be arbitrary），relationships between the nonlinear cubic coefficients are found.

The nonlinear stiffness coefficients are shown in Table 4，which are in good agreement with Eq.（38）.The validity of the method is verified again.The modal linear stiffness，equivalent stiffness，and total equivalent stiffness matrices at 160 dB are given in Table 5.

Table 4 Modal nonlinear cubic stiffness coefficient of metal stiffened plate

Table 5 Modal linear stiffness,equivalent stiffness,and total equivalent stiffness matrices obtained for the stiffened plate at an acoustic load of 160 dB

3.2 Result and analysis

The RMS fringe of displacement and acceleration responses obtained by linear analysis and EL analysis are shown in Table 6.The stiffened plate model in this paper has the same mass as the aluminum plate model in Ref.［18］.The part of the material where the thickness of the stiffened plate decreases relative to the aluminum plate is used as the stiffeners.Compared with the displacement response of the metal plate in Ref.［18］，the linear and EL analysis results are reduced by 0.32×10-2m and 0.10×10-3m，respectively，since the stiffeners increase the stiffness of the structure.The center displacement is obtained by linear and EL analyses.The frequencies corresponding to the resonant peaks obtained in the EL analysis continuously shift upward with the increasing pressure loading，and the difference between the fundamental and second mode frequencies is not constant，which is similar to the laminated plates in Ref.［18］.So，in this paper only the displacement response power spectral density（PSD）in the direction ofZof Node 165 in the center of stiffened plate is shown in Fig.3 at acoustic pressure loads of 160 dB.The acceleration response PSD in the direction ofZof the Node 165 in the center of stiffened plate under 160 dB is shown in Fig.4.

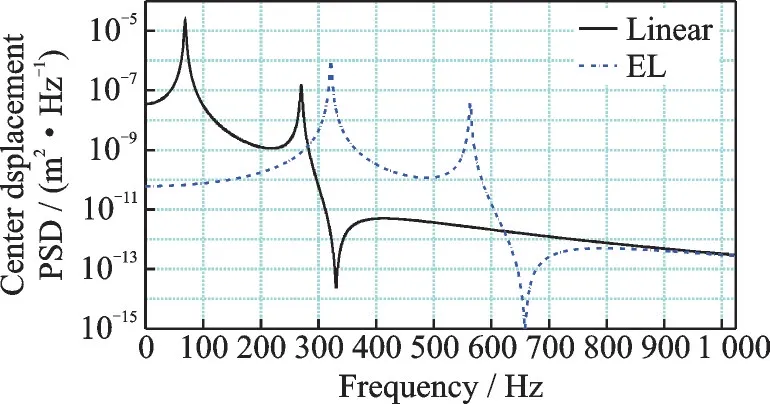
Fig.3 Comparison of displacement PSD in Z direction of Node 165 obtained by linear and EL analyses of stiffened plate at 160 dB

Table 6 Displacement and acceleration response RMS of metal stiffened plates by linear and EL analyses at 160 dB acoustic load

Fig.4 Comparison of acceleration PSD in Z direction of Node 165 obtained by linear and EL analyses of stiffened plate at 160 dB

It is found from Table 7 that the stress response of the beam element predicted by the linear analysis is larger than that by the EL analysis，that is，the linear analysis overestimates the response value.The finite element model for beam and plate assembly established in this paper can analyze the stress response at different locations of cross section of the beam element.As shown in Fig.1（b），the response results of pointCand pointDon the cross section of beam element are significantly different from the middle surface.The stress response RMS value of pointC，which is far from the middle surface of the plate，is greater than that of pointD，which is near the middle surface of the plate.The PSD distribution of stress response at pointCand pointDin the cross-section of beam element 608（along the direction of the short side）obtained from linear and EL analyses are shown in Figs.5，6.The PSD distribution of stress response at pointCand pointDin the cross-section of beam element 575（along the long side direction）obtained by linear and EL analyses are shown in Figs.7，8.By contrastive analysis from Figs.5—8，it is found that the stress response value of beam element 608，which is in short-side direction，is larger than that of beam element 575，which is in long-side direction.

Table 7 Beam stress responses RMS fringe by linear and EL analysis at 160 dB acoustic load

Fig.5 PSD distribution of stress response at point C in cross-section of beam element 608 obtained from linear and EL analyses at 160 dB acoustic load

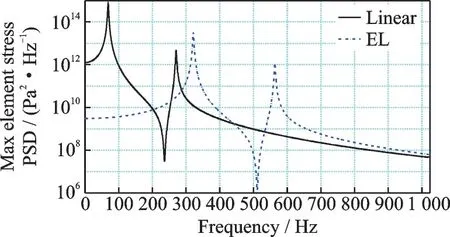
Fig.6 PSD distribution of stress response at point D in cross-section of beam element 608 obtained from linear and EL analyses at 160 dB acoustic load

Fig.7 PSD distribution of stress response at point C in cross-section of beam element 575 obtained from linear and EL analyses at 160 dB acoustic load

Fig.8 PSD distribution of stress response at point D in cross-section of beam element 575 obtained from linear and EL analyses at 160 dB acoustic load

The stress response RMS of shell elements with/without stiffeners，obtained by linear analysis and EL analysis at 160 dB acoustic pressure are listed in Table 8.The Von-Mises stress responses of the shell elements with/without stiffeners are significantly different.Because of the beam element bearing part of the stress，the maximum stress of the shell elements with stiffeners is not in the middle.The stress response PSD distribution results of shell element 140 obtained by linear and EL analyses are shown in Fig.9，where-Zis the unstiffened surface and+Zis the stiffened surface.

Table 8 Stress responses RMS fringe on surface with/without stiffeners of metal stiffened plates by linear and EL analyses at 160 dB acoustic load

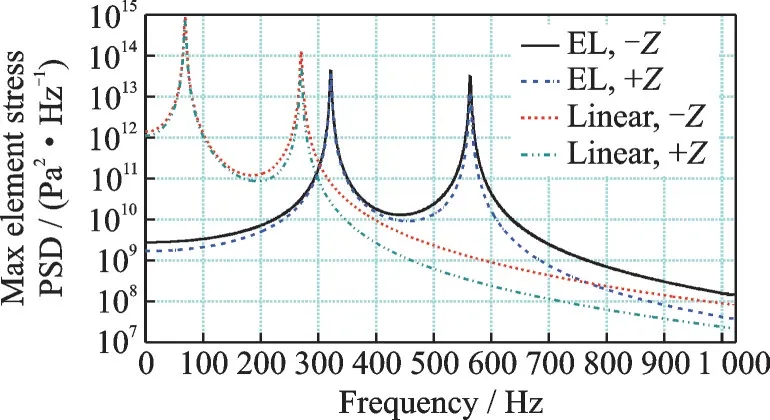
Fig.9 Von-Mises stress responses PSD of shell element 140 by linear and EL analyses at 160 dB acoustic load

4 Conclusions

The present study proposed an improved ROM-EL-FEM method to predict the geometrically nonlinear random response of simply-supported rectangular stiffened plates.The conclusions can be drawn as follows.

（1）The statistical dynamic response of shell elements and beam elements in the stiffened plates can be obtained，respectively.The stiffeners have significant influence on vibration modes of thin plate.There are obvious differences between the stress response of the shell element at the stiffened surface and unstiffened surface.Because the stiffeners enhance the stiffness of the structure，the displacement response of the stiffened plates is reduced compared with that of the unstiffened plates of the same mass in Ref.［18］.

（2）Because the stiffened plate present in this paper belongs to weak stiffened plate，its nonlinear characteristic is similar to that of thin plate.Nonlinearity in the vibration response of the stiffened plates is due to transverse deflection and in-plane stretching，which increases the stiffness of the structure，and consequently diminishes the displacement response.So，the frequencies corresponding to the resonant peaks obtained by EL analysis are higher than those obtained by linear analysis.The linear analysis do not account for this effect，which results in the prediction of exaggerated displacement responses under high acoustic pressure loading，leading to excessively conservative designs.

（3）The geometric nonlinearity plays an important role in the random vibration response of stiffened plates，particularly at high acoustic pressure loading.For the prediction of nonlinear random vibration response of stiffened plates，the basic model data have been given in this paper，which can contribute to analysis of the geometrically nonlinear random response for similar structures.

AcknowledgementsThis work was supported by the National Natural Science Foundations of China（Nos.11872079，11572109），the Science and Technology Project of Hebei Education Department（No.QN2019135），Advanced Talents Incubation Program of the Hebei University（No.521000981285）.

AuthorsDr.YANG Shaochong received the Ph.D.degree in mechanics from Beijing University of Technology，Beijing，China，in 2018.He is currently a lecturer of College of Civil Engineering and Architecture，Hebei University.His current research interests include structural dynamics，computational mechanics.

Prof.YANG Qingsheng received the Ph.D.degree in mechanics from Dalian University of Technology，China，in 1992.He is currently a full professor of Department of Engineering Mechanics，Beijing University of Technology.His current research interests include mechanical properties of novel materials and structures，macro-and micro-mechanics of composites，multi-scale computational mechanics method and application，multi-filed coupling performance of intelligent and biological materials.

Author contributionsDr.YANG Shaochong designed the study，built the models and wrote the manuscript.Mr.LI Youchen contributed to data collect and analysis.Prof.YANG Qingsheng guided the writing of the article，and revised the manuscript.Prof.WANG Jianmin contributed to the discussion and background of the study.All authors commented on the manuscript draft and approved the submission.

Competing interestsThe authors declare no competing interests.