非对偶性点云拓扑特征识别与过渡特征保护

张春亢，李红梅，张 霞

(贵州大学 测绘工程教研室，贵州 贵阳 550025)

1 引 言

作为一种基础算法与底层技术，三维点云特征提取与简化在模型配准[1]、模型重建[2]及信息识别[3]等方面得到了广泛应用。特征提取算法能否获得正确真实可靠的特征，并保证特征的完整性与拓扑一致性对点云数据的后续处理及其应用将产生巨大影响[4]。

因此，三维点云的特征提取与简化一直是学者研究的重点，大量算法被提出，如基于邻域信息[5-6]、曲面拟合[7-8]、聚类或区域分割[9-10]及数学模型[11-12]等的特征提取方法。这些特征提取常规算法对三维点云模型的轮廓线、棱线提取均取得了比较好的效果，但对于过渡特征线，或因为提取过程中过度强调特征线的闭合性而无法实现有效提取，或提取的特征线存在断裂、散乱、不完整的现象，使得难以根据这些特征线对模型进行区域分割或网格划分[9-10]。此外，建立拓扑关系正确的三维模型一直是点云数据模型(如建筑物模型)重建的重点与难点[13]，现有算法在构建特征线时建立并保证其正确的拓扑关系比较困难，也难以有效揭示点云模型表面的拓扑形态。

Morse理论经过微分拓扑学验证，相比于目前主流的点云特征提取方法，是一种有严格数学理论基础的表面拓扑特征构建方法，基于其提取的Morse-Smale(MS)复形在理论上符合拓扑完整性与一致性，提取的点云特征线不仅清晰、紧致、完整，能够实现对点云模型表面的完全分割，而且能在特征简化过程中根据需要构建特征的多层次表达体系，是对大规模科学数据进行分析与可视化的强大工具[14]。根据特征重要性度量方法不同，目前基于Morse理论的特征识别算法主要有点持续值法[15]、线持续值法[16]和线-复形差值法[17-18]。文献[15]基于Morse理论首先实现了三维模型MS复形的提取，然后以“持续值(persistence)”简化理论与技术[4]为基础，通过“同态收缩算法”[19]完成简化，这种简化方法实质上是一种基于特征点度量指标差值的方法；文献[16]首先基于Morse理论实现了MS复形的提取，然后以“关键线持续值(separatrix persistence)”作为线的显著度度量指标完成简化；文献[17-18]首先通过网格度量指标提取初始MS复形，然后根据特征线上的平均度量指标值与其邻接区域平均度量指标值的差值对特征线进行优先排序，最后基于“同态收缩算法”完成拓扑简化，实现模型主要特征的识别，该方法实质是一种改进的线持续值法。另外，文献[20]利用MS复形四边形的稳定性，利用线-复形差值法对破损文物模型的拓扑特征进行了提取与简化，然后运用几何拓扑图形进行搜索匹配，实现了文物模型的拼接；文献[21]利用Morse理论标定、提取出了点云模型的潜在特征点，避免了模型的局部曲面拟合或重建，但后期特征线的识别与提取仍然采用常用算法，没有充分利用Morse理论提取特征线，提取的特征线不具有MS复形的特性，无法实现基于Morse理论的拓扑简化与多层次表达。

由于Morse理论是基于具有对偶性的二维标量场提出的，基于其提取的MS复形也是一种适用于对偶性二维标量场的拓扑数据结构[22]，现有基于二维和三维点云的拓扑特征提取、特征重要性度量及拓扑特征简化也是基于MS对偶性实现的。而以曲率、法向量改变量为度量指标的三维点云模型是一种非对偶性模型，现有文献在提取三维点云MS复形时，提取结果中含有大量无意义甚至错误的特征，不利于点云数据的后续处理与应用。另外，有研究与实验发现，基于Morse理论的拓扑特征提取与简化是一种比较耗时的拓扑模型构建理论与算法[14]，无意义拓扑特征的提取与简化额外消耗了大量不必要时间。

针对Morse理论由具有对偶性的二维标量场推广到非对偶性三维点云模型时遇到的问题，本文提出了单复形拓扑模型，推算了单复形模型特征线重要性度量方法和单复形拓扑模型的简化算法，以避免无意义特征的提取并提高时间效率。同时，针对模型过渡特征在简化过程中难以保留的问题，提出了模型过渡特征保护方法，最后用典型的三维点云模型对本文模型与方法进行了验证与分析。

2 单复形拓扑模型提取

2.1 问题与概念

对于一般的二维标量场，如地形场[4]、温度场[23]等，其度量指标，如高程大小、温度高低等是一个基于一定基准(如高程基准、绝对零度等)的宏观概念，这种标量场的特征是基于某一个参考面具有一定的对偶性，其基于Morse理论提取的MS复形也具有对偶性，提取的上升线对应着标量场的脊线(ridge)，提取的下降线对应着标量场的谷线(valley)，即提取的脊线和谷线与现实标量场的形状构成相符，如图1(a)所示的地形场及其MS复形。本文称这种MS复形为对偶复形拓扑模型。

在三维点云模型特征提取过程中，曲率、法向量的变化等为常用的计算度量指标，这些度量指标是一种微观概念，以其为度量指标形成的场模型不具有基于某一参考面的对偶性。因此，采用这些度量指标提取的MS复形也不具有对偶性，如图1(b)所示，其基于Morse理论提取的三维表面模型的脊线包含模型的凸起轮廓线与棱线(如图1(b)中的特征线pk2-sad3-pk3)和凹陷轮廓线与棱线(如图1(b)中的特征线pk1-sad1-pk3)，它们构成了三维点云模型的真实有价值特征，而提取的谷线(图1(b)中的虚线)均是没有实际意义甚至错误的特征。因此，提取的脊线和谷线与现实三维表面模型的形状构成不相符，本文称这种拓扑模型为单复形拓扑模型。

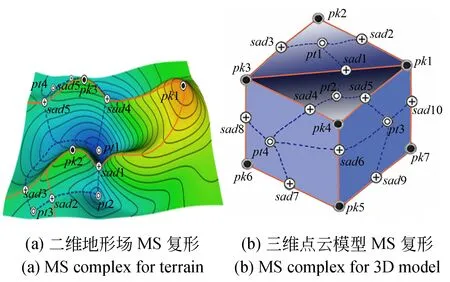
图1 二维与三维场模型及对应MS复形Fig.1 2D and 3D scalar fields and corresponding MS complexes

因此，在将Morse理论由二维标量场推广到三维点云模型的应用过程中，提取的MS复形会存在大量无意义的特征，这些特征不利于后续的数据处理与进一步的应用，如具有光滑平面的三维表面模型中，每个鞍点连接的两个极小点的度量指标值均接近为0，现有的基于“持续值(persistence)”的简化操作，需要对对偶复形中的特征点进行配对，这就造成了一定的配对困难。另外，作为一种非常耗时的拓扑特征构建与简化方法，没有实际意义的拓扑特征构建与简化将消耗大量不必要的时间。

2.2 单复形提取

法向量是曲面的一阶微分量，与曲面的二阶微分量曲率比较，计算更简单高效，本文选用点法向量的变化量作为点的度量指标。

(1)特征点识别：在三角网模型中，对于顶点v，如图2所示。若一阶邻点的度量指标值均大于v点，则v是极小点；若一阶邻点的度量指标值均小于v点，则v是极大点；在其与一阶邻点的逆(顺)时针比较中，记度量指标差正负符号的变化次数为CN，若CN为2，则顶点v是正则点；若CN为4，则顶点v是单鞍点，若CN大于4，则顶点v是多鞍点。

(2)单复形拓扑模型构建：在构建基于Morse理论的单复形拓扑特征时仅需要构建脊线，而不需要构建谷线。首先展开多鞍点，然后从鞍点出发，两条特征线分别沿着度量指标值增大的方向寻径直到极大值点(上升线)结束。对于上升线从鞍点到极大点的寻径方式，目前有三种常用方法：最大邻点法、最大角度法和梯度法，其中前两种方法生成的特征线将沿着三角网的边前进；梯度法沿着三角形中真实梯度寻径，该方法最接近真实情况，但会将三角形分割为两部分，需要对现有三角形进行分割，重新调整三角网及其拓扑关系，计算量大。如图2所示，与点V比较，P3有更大的指标值，P1与P2有更大的角度值，采用最大邻点法寻找下一点为P3点，采用最大角度法为P1或P2，梯度法为P1P2之间的P0。本文采用最大邻点法，若p点为v点的下一个寻径点，其符合如下条件：

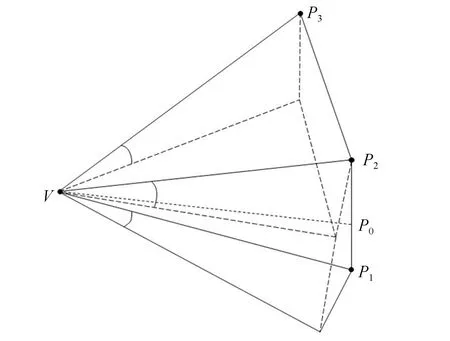
图2 特征线寻径方法Fig.2 Routing method by finding the next point

(1)

其中：pi为v的邻点，n为点v的邻点个数。

3 单复形模型拓扑简化推导

3.1 特征线重要性度量推算

基于Morse理论的拓扑特征提取算法是一种敏感性较强的算法，在进行模型特征提取时，其不但能识别出点云的主要特征与各层次过渡特征，而且会提取一定的噪声，对于提取的单复形拓扑模型，需要通过拓扑简化剔除模型噪声，并根据需要建立特征的多层次表达。

在进行拓扑简化前，首先需度量拓扑特征重要性，对拓扑特征的重要性进行排序。在MS复形的拓扑简化过程中，目前研究的特征重要性度量方法有基于特征点[4,15]和基于特征线[16-18]两种，在三维点云中，特征线往往比特征点更有价值，在MS复形中，定义每个鞍点连接的两条升弧和两条降弧分别为一条特征线, 作为特征重要性度量和操作的基本单元，即为l，文献[18]“关键线持续值(separatrix persistence)”度量方法中，脊线和谷线的重要性为:

(2)

其中：pl(x)为特征线上一点x的度量指标；max(f(mk))为与l上的鞍点连接的两个极小点中的较大值；min(f(Mk))为与l上的鞍点连接的极大点中的较小值，其中，k=1,2。

在三维点云MS复形中，极小点度量指标值趋近为0。因此，对于单复形拓扑模型，式(2)中对应的脊线公式为:

pl(x)=f(x)-max(f(mk))≈f(x).

(3)

则单复形拓扑模型特征线的重要性度量指标RI可以定义为：

(4)

其中：n为特征线l上的特征点的数量。

基于特征线度量指标的重要性度量方法有一定的片面性，例如，对于建筑物等棱角分明的接近方体的三维点云模型，由于其棱线度量指标值相近、面接近为平面，其计算得到的特征重要性值大小接近，在简化过程中，一些显著度不强的主轮廓线特征被删除，而显著度强的细微特征甚至噪声被保留。对于这类三维表面模型，研究联合特征线度量指标与复形面积的综合性计算方法更有价值，定义联合特征线度量指标和复形面积的重要性计算方法为：

NRS=λ*NRI+(1-λ)*min(NSk)，

(5)

其中:NRI为特征线l的归一化重要性度量指标，min(NSk)为与特征线l关联的两个脊线围成的复形C中面积较小复形的面积归一化指数，其中，k=1,2。λ为权重。三维点云单复形拓扑模型生成采用最大邻点法，特征线沿三角形边寻径, 则C的面积S近似为C内所有三角形面积的和，即为：

(6)

其中，At为复形C中第t个三角形的面积。

3.2 拓扑简化推导

MS复形简化的基础是Pfaltz[19]提出的“同态收缩算法”，如图3所示，对于简化前的图3(a)，极小点pt1与鞍点sad1是符合“持续值(persistence)”最小的一对临界点，其被删除的同时，与鞍点sad1关联的脊线pk1-sad1-pk2被同步删除，原来与极小点pt1连接的谷线直接连接到极小点pt2，如图3(b)所示，简化后的MS复形特征点仍然符合欧拉公式，特征线保持拓扑一致性与完整性。该简化过程建立在MS复形对偶性质基础上，在简化过程中，具有对偶性的脊线或极大点与极小点或谷线均参与了计算。

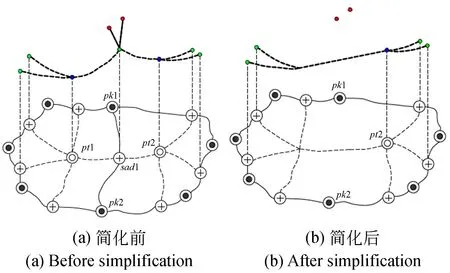
图3 对偶性SM复形同态收缩算法Fig.3 Homomorphic shrinkage algorithm of MS complex

本文提出的单复形拓扑模型不再满足MS复形的对偶性，如图4所示，在单复形拓扑模型中，通过对特征线的重要性度量排序，特征线pt1-sad1-pk2是需要删除的特征线，在对其进行删除时，在对偶复性拓扑模型中，需要同步删除的还有鞍点sad1及与sad1连接且指标差较小的极小点，其与sad1组成临界点对。但在单复形模型构建时没有提取pt1，所以相当于该点已经被删除了，结果如图4(b)。因此，在简化过程中保证了单复形拓扑模型的拓扑一致性与完整性。

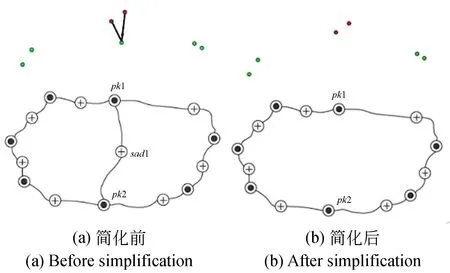
图4 单复形拓扑模型简化Fig.4 Simplification method of the single complex

4 过渡特征保护方法

根据Morse理论的关键线构建方法，鞍点是特征线构建的起始点和驱动点，所有从鞍点出发的上升线，均沿指标值增大的方向寻径，并结束于极大点。部分位于非轮廓线或棱线上的鞍点构建关键线时，结束于轮廓线或棱线的极大点上，其所构造的关键线部分位于较光滑平面或曲面上，部分位于模型的轮廓线或棱线上(如图5所示)。在利用基于特征线的重要性度量方法进行特征重要性度量时，这类关键线的重要性度量指标往往会大于过渡特征线重要性度量指标，从而造成简化过程中过渡特征被删除，非特征线被保留的问题。

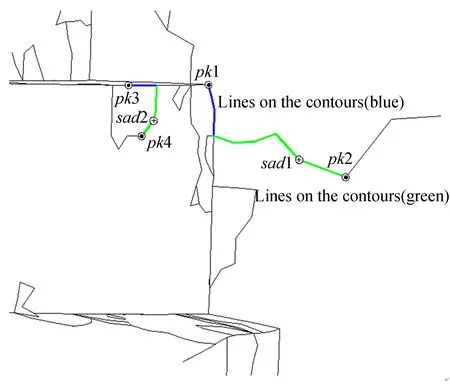
图5 跨轮廓与非轮廓的关键线Fig.5 Critical lines crossing contours and surfaces

依据基于Morse理论的拓扑特征构建与简化理论，在构建复形特征前删除鞍点，不影响特征的拓扑完整性和一致性。对于需要保留过渡特征的点云模型，按照下面特征提取与简化步骤处理，实现对过渡特征的保护：

(1)基于Morse理论提取模型极大点和鞍点；

(2)设定阈值，删除度量指标小于阈值的鞍点，避免非特征线的构建；

(3)设定阈值，依据“持续值(persistence)”简化理论与技术，删除度量指标大于阈值的鞍点；

(4)基于删除简化后的模型特征点，构建单复形拓扑模型；

(5)计算特征线重要性度量，并设定阈值，对提取的复形进行拓扑简化，获取点云模型特定细节层次特征。

5 实验与分析

采用C++编程语言，在VS 2010上完成算法实验，标准PC平台的配置为8 GB内存、Intel(R) Core(TM) i7-7700HQ CPU @ 2.80 GHz处理器。

5.1 算法效率

实验数据为Gate点云模型，首先将其构建成三角形，如图6(a)，计算各个顶点的度量指标值，如图6(b)。提取了Gate模型的初始单复形拓扑模型，如图6(d)，作为对比，根据文献[17-18]提出的“线-复形差值法”提取了Gate模型的初始MS复形，如图6(c)。单复形拓扑模型不但识别出了模型的轮廓线、棱线，也识别出了模型的过渡特征和一些噪声，而MS复形识别出单复形中有效特征的同时，提取出了大量无意义特征，图6(c)中模型光滑区域存在大量特征线。由表1可知，基于Morse理论的拓扑特征构建是一种非常耗时的特征提取方法，与文献[17-18]提取点云模型初始MS复形比较，初始单复形拓扑模型的构建时间效率提高了52.22%，数据压缩率提高了5.09%，且通过对模型进行简化可以获取更高的数据压缩率。

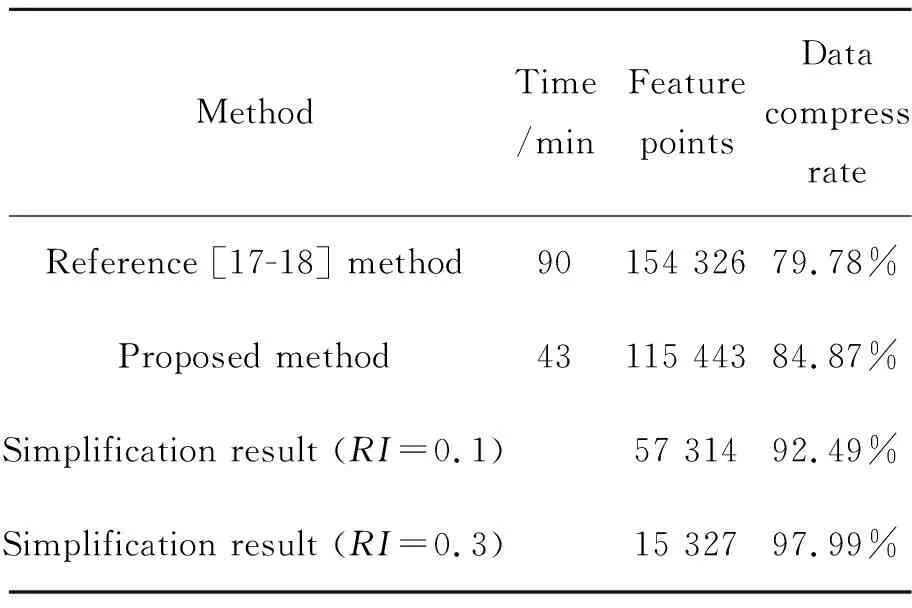
表1 Gate模型不同提取方法效率对比

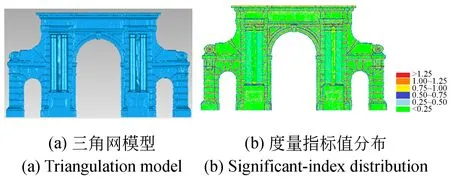
图6 Gate模型试验结果Fig.6 Results of Gate model

基于公式(4)计算的特征线重要性，利用推导的单复形拓扑简化算法进行简化，设定不同的阈值，逐步删除噪声和过渡特征，在RI=0.1时，简化结果很好地保留了模型的轮廓线，并保持了拓扑特征的完整性与一致性，如图6(e)所示。但该算法是一种完全基于线度量指标的简化算法，简化过程中删除了一些指标值不显著的轮廓线特征，如建筑物圆柱曲面上的特征线，保留了重要性指标值较大的细微特征。利用联合特征线度量指标与复形面积的综合度量指标对初始单复形模型进行了简化，如图6(f)所示，其与图6(e)具有大致相同的数据压缩率，但提取的结果保留了更多的主轮廓线，如建筑圆柱曲面上的特征线，删除了更多的细微特征。由于建筑物模型棱角分明，特征线度量指标归一化后，其值大部分趋近于1，复形面积归一化后，其值符合正态分布，所以特征线度量指标的权重设置较小，仅为0.2。

5.2 过渡特征保护

Fandisk点云模型的棱线特征具有渐变性，含有一定的过渡特征，是检验特征提取算法的理想模型。文献[17-18]提取的初始MS复形存在大量无意义的特征线，如图7(a)，本文单复形拓扑模型在避免无意义特征提取的同时，有效提取了模型的主轮廓线、各层次过渡特征和部分噪声，如图7(b)。对于图7(b)，按照推导的关键线重要性度量方法进行简化，阈值为0.4时，结果如图7(c)所示；对于图7(a)，利用文献[17]提出的“线-复形差值法”进行简化，结果如图7(d)所示。图7(c)～(d)结果显示(彩图见期刊电子版)，由于现有基于特征线指标的重要性度量方法存在的问题，简化过程中部分噪声未被简化删除时，部分过渡特征被简化删除(图7(c) ～ (d)蓝圈部分)。文献[10]为目前主流的三维点云特征提取常规算法，其提取结果如图7(e)所示，其提取的特征线在过渡特征部分仍然存在一定程度的局部断裂、不连续(图7(e)蓝圈部分)、或特征识别不完整(图7(e)红圈部分)的情况。利用本文提出的过渡特征保护处理方法进行特征提取，结果如图7(f)所示，本文过渡特征处理方法明显改善了特征线在过渡特征部分的断裂、不完整问题，对模型过渡特征的有效识别率达到了100%，起到了对过渡模型特征的保护作用，提取结果可实现对三维点云模型表面的完全分割，并可以通过设定简化阈值提取不同层次的过渡特征。但由于现有的特征线重要性度量方法仍然存在一定的片面性，本文方法简化后的模型存在少量噪声特征线没有被删除。

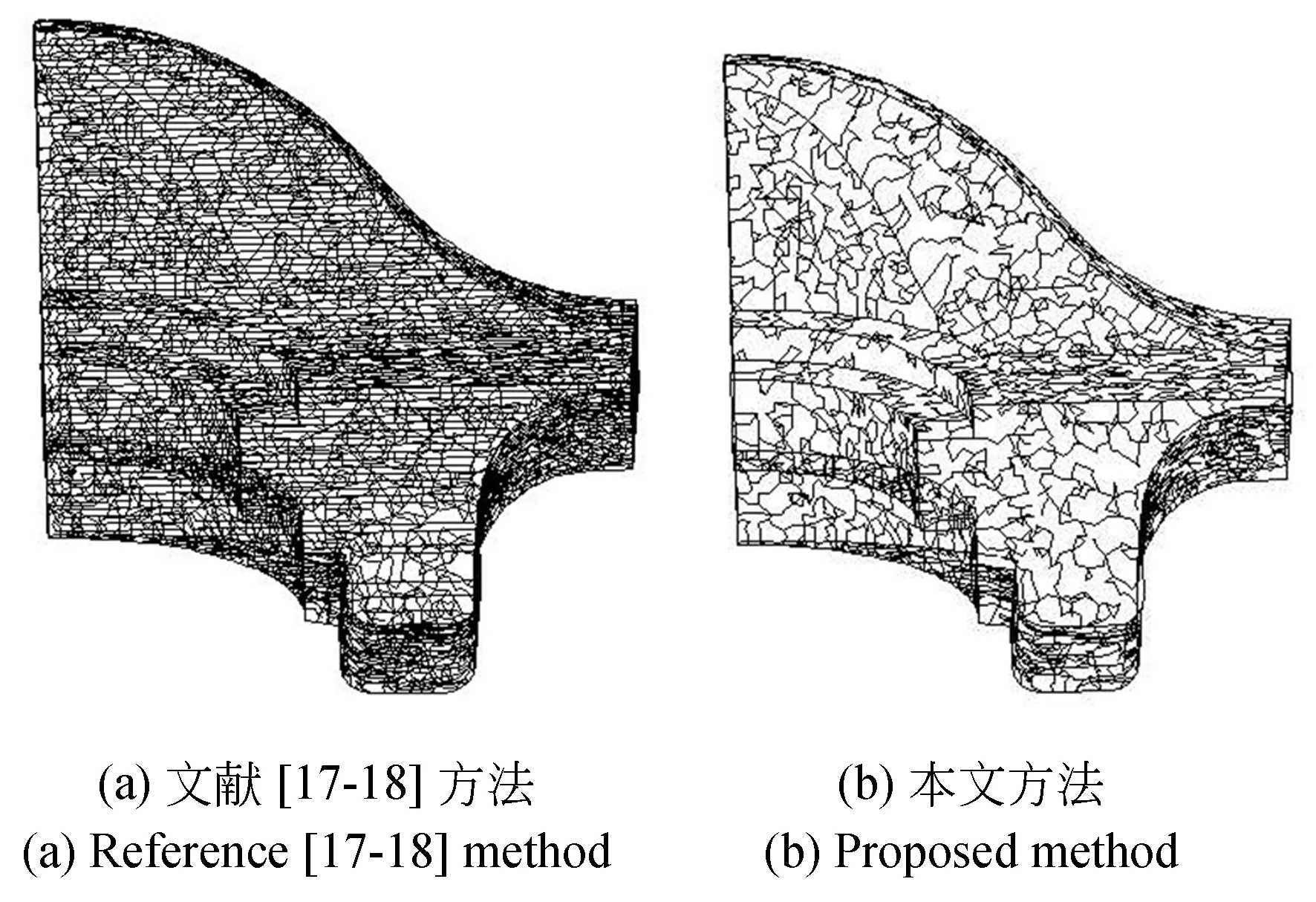
图7 不同方法特征提取效果对比Fig.7 Feature extraction results of different methods

5.3 其他实验模型

图8给出了其他模型实验结果，其中Bunny模型为更复杂的三维点云模型，且其轮廓线不突出鲜明，经过复形提取与拓扑简化，模型的主轮廓线得到了有效识别，用较小的数据量揭示模型的三维形状特征与拓扑形态，特征线的识别率达到了90%以上；Canstick模型和贵州大学专家楼模型为较为简单的点云模型，其特征识别的完整率达到了100%，可以满足模型三维重建等实际工程的需要。

图8 其他模型实验Fig.8 Experiment of other models

6 结 论

更严谨的数学理论基础使Morse理论在三维点云拓扑特征提取与建模方面更有优势。针对三维点云模型非对偶性导致的拓扑特征提取与简化问题，提出了单复形拓扑模型提取和相关简化算法，实验表明，新的提取方法避免了三维点云模型无意义特征的提取，比现有方法在时间效率上提高了52.22%，数据压缩率提高了5%以上；过渡特征保护方法对点云模型过渡特征的识别率达到了100%，明显改善了常规算法特征线在过渡特征部分的断裂和不完整问题，为三维点云数据在模型重建、逆向工程、智能制造等方面的应用提供了更精确可靠的模型基础。

对于部分点云模型，采用目前的特征重要性度量方法进行简化，仍然难以删除部分次要特征甚至噪声。另外，特征线的简化过程即是面与面之间的合并过程，现有特征重要性度量方法仅仅考虑了线或面本身的各种参数指标，并未考虑模型结构单元之间的相对空间关系，导致简化时部分模型结构单元之间的合并不符合实际(如建筑物立面与平面合并)。这些是下一步需要研究解决的问题。