变间距凸面光栅成像光谱系统的消像散设计
2020-11-24赵美红王新宇姜岩秀李文昊
赵美红,王新宇,姜岩秀,杨 硕,李文昊*
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
1 引 言
成像光谱仪是一种以高分辨率同时获取每个探测目标的图像信息和特征光谱信息的辐射遥感仪器,其“图谱合一”的特点不仅可以帮助人们直观地确定探测目标的存在,而且可以实现对材料成分微观细节的分析。因此,成像光谱仪可用于执行对广域精确制图、军事目标的识别与鉴定、目标检测、过程监控控制、临床诊断、影像学以及环境评价等探测任务[1]。目前,成像光谱仪已经发展成为很多领域不可或缺的一部分,并在生物制药、食品安全、农林、加工制造、国防安全、海洋监测、矿物勘探及空间探测等领域[2-6]具有广阔的应用前景。
成像光谱仪按照扫描成像方式一般分为推扫型、摆扫型和凝视型三种。其中,推扫型[7]成像光谱仪在像面处的探测器采用面阵CCD,它随搭载平台沿轨方向的推扫而实现对探测目标的二维空间信息和一维光谱信息的实时获取,从而实现高空间分辨率与光谱分辨率成像。以凸面光栅为核心分光元件的成像光谱仪采用全反射式Offner同心结构的光谱分光系统,结构简单紧凑,色差、谱线弯曲和畸变小,分辨率高且成像速度快,因此成为推扫型成像光谱仪应用领域的首选。
然而,反射式、对称结构的成像光谱系统在成像时一般会因光学元件的离轴配置而受系统像散的影响,因此,减小系统像散是该类系统在优化设计时首要考虑的问题。目前,已经有一些借助光学设计软件优化设计凸面光栅成像光谱仪的方法,如倾斜凸面光栅,对凹面反射镜加离心,将凹面反射镜一分为二并优化其曲率半径与离轴量,以及在光路中加入消像散的弯月透镜等[8]。这些消像差方法虽然能够减小一部分系统像差,在一定程度上满足应用需要,但是会使得系统复杂化,增加系统负荷,从而增大仪器加工和装调的难度,不仅大大提高了仪器的研制成本,还会破坏原有系统的反射式结构,使其应用受限。
像差是影响光谱仪器分辨率的重要因素,而影响光栅像差的两个因素分别是光栅的基底面形和刻线密度及形状。理论分析表明,通过改变光栅的刻线密度分布或是光栅面形可以消除系统像差。1960年,Murty研究了变栅距圆条纹凹面光栅的成像特性,确定了刻线密度的变化可以消除部分像差[9-12],之后,人们开始展开对变间距光栅的研究。目前,用于光谱仪器像差校正的变间距光栅主要是变间距的平面光栅和凹面光栅,还未见变间距凸面光栅用于成像光谱仪像差校正的报道。
本文基于凸面光栅成像光谱系统的几何像差理论模型[13],分析了系统的聚焦情况,并通过计算离轴物点的子午聚焦曲线、弧矢聚焦曲线以及它们的位置关系,构建了凸面光栅刻线函数与像散的数学模型,设计出了变间距的消像差凸面光栅,并以此为色散元件简化了分光系统的结构,降低了系统的设计与研制难度,为凸面光栅成像光谱仪的消像差设计提供了一种新思路。
2 凸面光栅成像光谱系统的消像差设计理论
2.1 几何像差理论模型
图1所示为三光学元件的凸面光栅成像光谱系统,M1和M2是两个凹面反射镜,G为凸面光栅,S和分别是系统的物平面和像平面,三光学元件的顶点O1,O2,O与物面中心A0、像面中心B0在同一水平面内(即该系统的子午面),而且在A0,O1,O,O2,B0处建立的直角坐标系的XS,x1,x,x2,X轴也在子午面内。A(0,s,z)点是物面上一入射点光源,由A点发出的光线经过M1镜上一点Q1(ξ1,w1,l1)反射后,与凸面光栅表面交于一点P(ξ,w,l),由凸面光栅上P点衍射后与M2镜表面交于一点Q2(ξ2,w2,l2),然后由M2镜聚焦于像面上一点B(0,Y,Z)。子午面上A0O1,O1O,OO2,O2B0的距离大小分别为r1,r,r′,r2,其中A0O1与x1轴的夹角为θ1,O1O与x轴的夹角为θ,子午面上O点的衍射角为θ′,OO2与x2轴的夹角为θ2。θ1,θ,θ′和θ2的正负分别取决于其对应的点和光线所在的坐标系x1y1z1,xyz和x2y2z2的第一象限或第四象限。

图1 三光学元件凸面光栅成像光谱系统Fig.1 Schematic diagram of three-element imaging spectrum system with convex grating
在该系统中,凹面反射镜M1,M2和凸面光栅G的面型均为球面,而且满足方程:
(ξτ-Rτ)2+ωτ2+lτ2=Rτ2,
(1)
其中Rτ表示球面曲率半径,τ=0,1,2分别代表凸面光栅G和凹面反射镜M1,M2。依据Namioka的几何像差理论,式(1)可以展开为坐标ωτ和lτ的级数,即:
(2)
点光源A发出的光线经过整个分光系统后的光程函数为:
(3)
式中:qτ,pτ分别为凹面反射镜(或凸面光栅)上入射光线和出射光线的光程;n为凸面光栅上入射点P对应的第n条刻线,定义光栅面顶点处为第零条刻线;m为光栅衍射级次;λ0为光栅的记录波长,λ为系统的使用波长;Mijkh,Hijkh分别表示系统结构参数和光栅制作参数引入的像差项,i,j,k,h表示凸面光栅成像光谱系统的像差项数;Hijkh[13]为与光栅刻线函数相关的项,随光栅刻线密度的变化会对系统像差进行调制。光栅刻线函数的级数展开式为:
(4)

对光程函数使用费马原理,可以得到像面点列图函数,即:
(5)
(6)
式(5)和式(6)即为凸面光栅成像光谱系统的几何像差理论模型,Eijkh,Fijkh为像差系数。
2.2 凸面光栅成像光谱系统的聚焦情况分析
当系统的凹面反射镜与凸面光栅的结构配置合理时,系统的离焦系数项E1000,F0100的值为零,近轴光线在像平面上的子午像与弧矢像聚焦。依据几何像差理论模型,以子午面上的像点聚焦条件E1000=C1000A1000+C0001=0为例,可得:
(7)
式中:
(8)


图2 Offner同心结构的罗兰圆示意图Fig.2 Schematic diagram of Rowland circles for concentric Offner configuration
(9)
式中:
(10)
由式(10)可以看出子午像点的成像位置是与光栅刻线函数的二阶项n20相关的函数,该项直接影响光栅的栅距;同样,可以得出弧矢像点的成像位置与光栅刻线函数的二阶项n02相关的函数,该项对光栅刻线的形状有影响。弧矢像点的聚焦距离为:
(11)
式中:
(r2)S=r′+
(12)
一般情况下,一个实际的点光源或像经过一个具有完美对称性的椭圆反射镜或超环面反射镜系统时,系统配置会满足聚焦条件(r2)M=(r2)S而成无像散像。但是,因色散作用,凸面光栅成像光谱系统不再具有完美的系统对称性,而且随着使用光谱范围的增加,这种不对称性影响越大,由此产生的像散也越大。近轴光线的系统像散可以表示为:
(13)
Last是与光栅刻线函数的系数项n20,n02相关的函数,式中ε(λ)是不同波长对系统像散影响的权重因子,以此为优化目标的适应度函数,并通过光栅刻线函数的高阶系数项(与系统的高阶像差相关)的调制,可以实现对系统主要像差——像散的优化。在该结构中,系统像差主要是由物、像光线不对称性引起的,一般通过对设计波长处的子午与弧矢聚焦曲线进行优化[1,14],使系统结构在该波长处满足像方远心[15-16]条件,就可以获得满足设计要求的优化结果。
3 凸面光栅成像光谱仪的消像散设计
凸面光栅作为Offner同心成像光谱系统的关键色散元件,同时又处于分光系统的光阑位置,决定着成像光谱仪的光学性能。为了得到高像质、高分辨率、低加工成本以及低装调难度的标准Offner成像光谱系统(如图3所示),本文通过优化凸面光栅刻线间距的设计方法,以减小并均衡不同波长的光线因色散不对称性引入的系统像散。
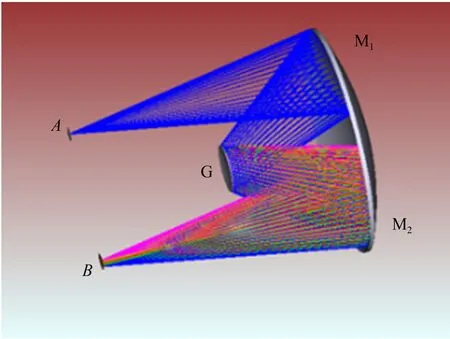
图3 凸面光栅成像光谱系统示意图Fig.3 Schematic diagram of imaging spectrum system with convex grating
在该设计中,凸面光栅G和凹面反射镜M均为球面,且其球心位于同一坐标处,两光学元件共轴,简化了系统结构。其中,狭缝尺寸为10 mm10 μm,凸面光栅的曲率半径为R=100 mm,光栅中心点处的刻线密度为100 gr/mm,光栅口径约为30 mm30 mm,光栅衍射级次为-1级,反射镜M的曲率半径为R1=R2=193.2 mm,主光线在光栅上的入射角为θ=30°,光谱波段为300~800 nm。以上述参数为结构优化设计的基本结构参数,为实现对多变量非线性目标函数的全局优化,选用高效率的遗传算法进行优化,并通过多组优化结果的对比筛选出最优的设计结果。

表1 变间距凸面光栅的设计结果

图4 光栅周期随空间位置变化的示意图Fig.4 Schematic diagram of grating period changing with space position
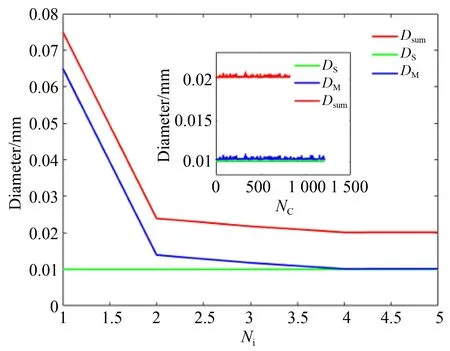
图5 在子午与弧矢方向的优化结果Fig.5 Optimal results in both meridional and sagittal directions
系统在设计波长处的全视场光线追迹结果如图6所示,分辨力优于2.4 nm;如图7、图8所示,系统在600 nm处有极限分辨力1.9 nm,在800 nm处的分辨力优于3.3 nm。在系统的相对孔径为F/2.7时,对300,600,800 nm的波长分别在0,0.7和1视场处对10 μm10 μm的物点进行光线追迹,得到的点列图如图9所示。图中,点列图是对均匀取样光线追迹的结果,实际的能量分布满足高斯分布,即光斑能量主要集中在谱线半高位置,如600 nm、0.7视场处的点列图所示,能量集中分布在直径约为10 μm的光斑范围内。整个系统的极限分辨力达1.9 nm,可实现约201个高光谱通道。
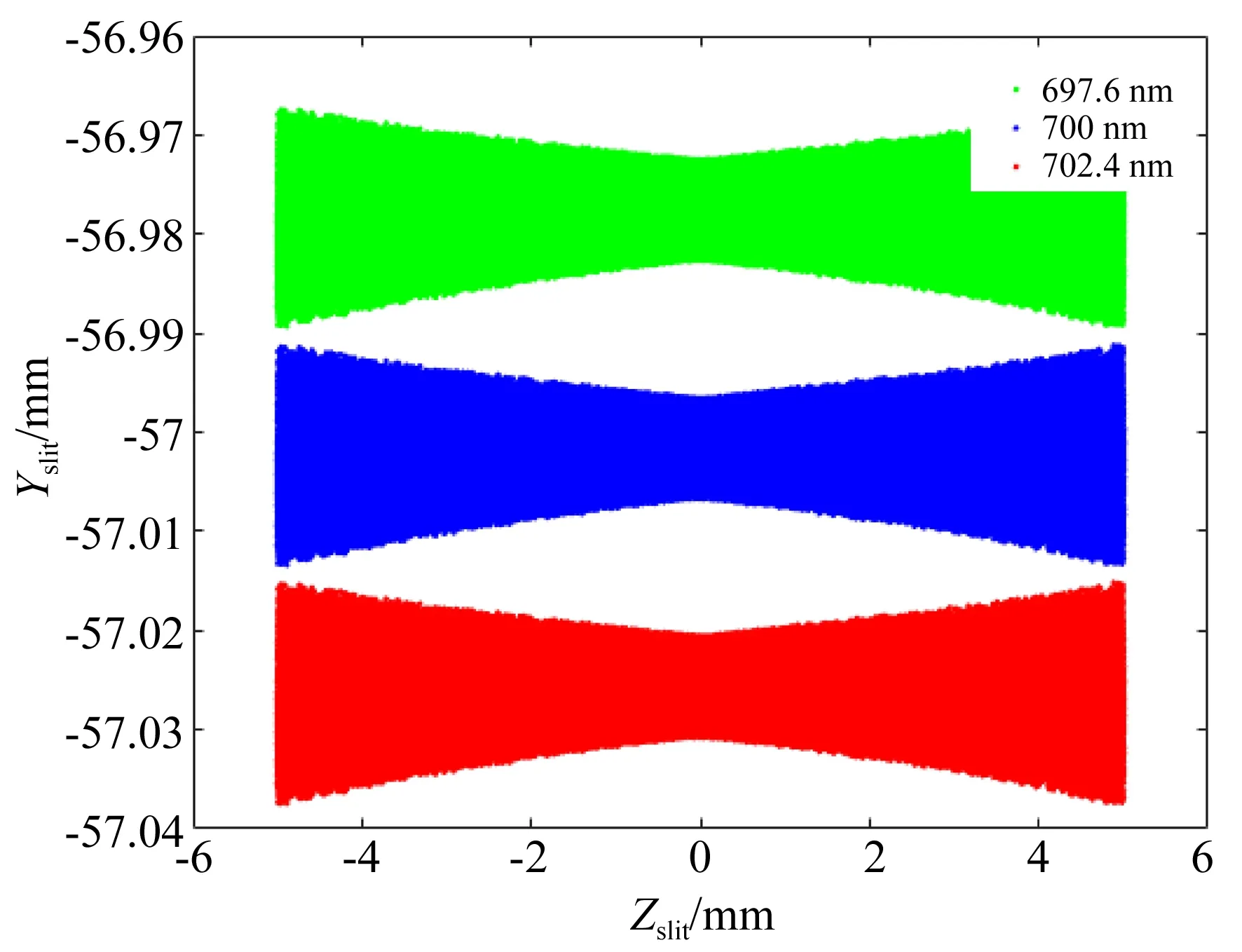
图6 (7002.4)nm波长的全视场光线追迹结果Fig.6 Ray tracing results at wavelengths of (7002.4)nm for whole field of view
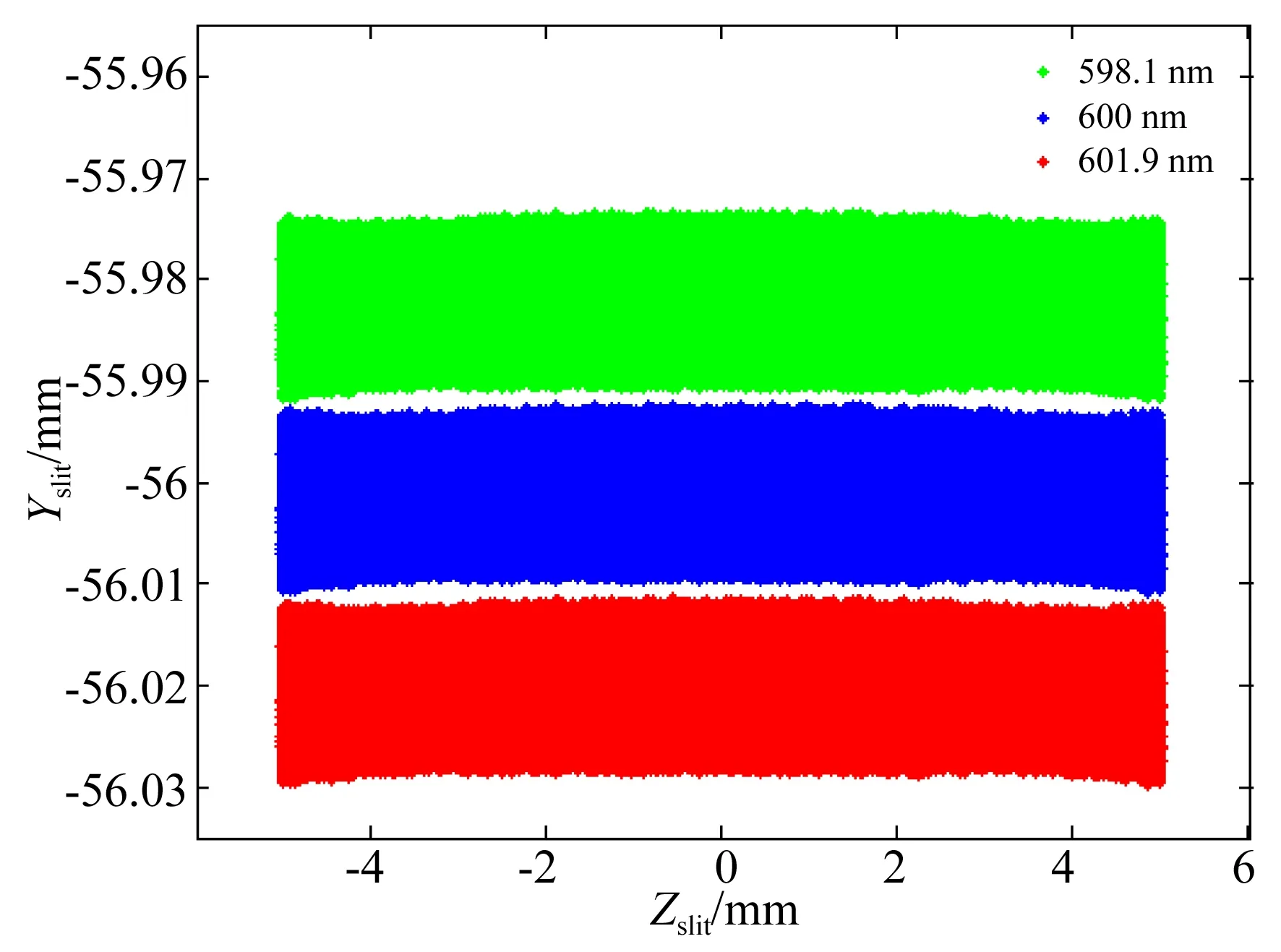
图7 (6001.9)nm波长的全视场光线追迹结果Fig.7 Ray tracing results at wavelengths of (6001.9)nm for whole field of view
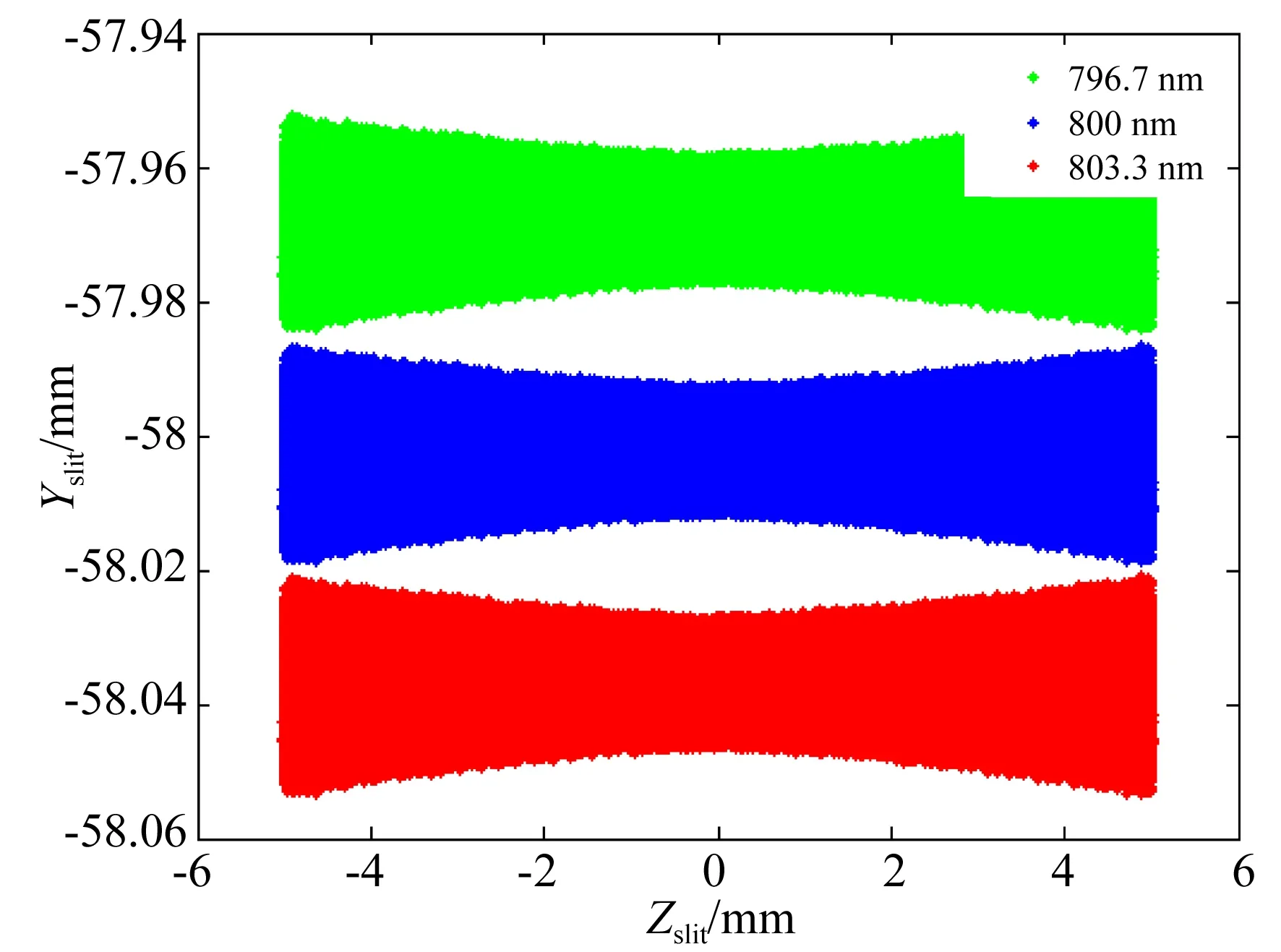
图8 (8003.3)nm波长的全视场光线追迹结果Fig.8 Ray tracing results at wavelengths of (8003.3)nm for whole field of view

图9 不同波长、不同视场处的点列图Fig.9 Spot diagrams at multi-wavelengths for different fields of view
在成像光谱系统中,谱线弯曲会导致光谱混叠,色畸变会使像面强度空间分布不均匀,一般要求谱线弯曲和色畸变均不超过探测器像元尺寸的一半。凸面光栅成像光谱系统是基于1∶1倍率放大的Offner同心对称结构,其色畸变因系统对称性消除,设计结果如图10所示。其中,横轴为光谱维方向,纵轴为每个波长狭缝像的长度相对于设计波长狭缝像的长度差,可见系统色畸变可以忽略。系统的谱线弯曲变化曲线如图11所示,
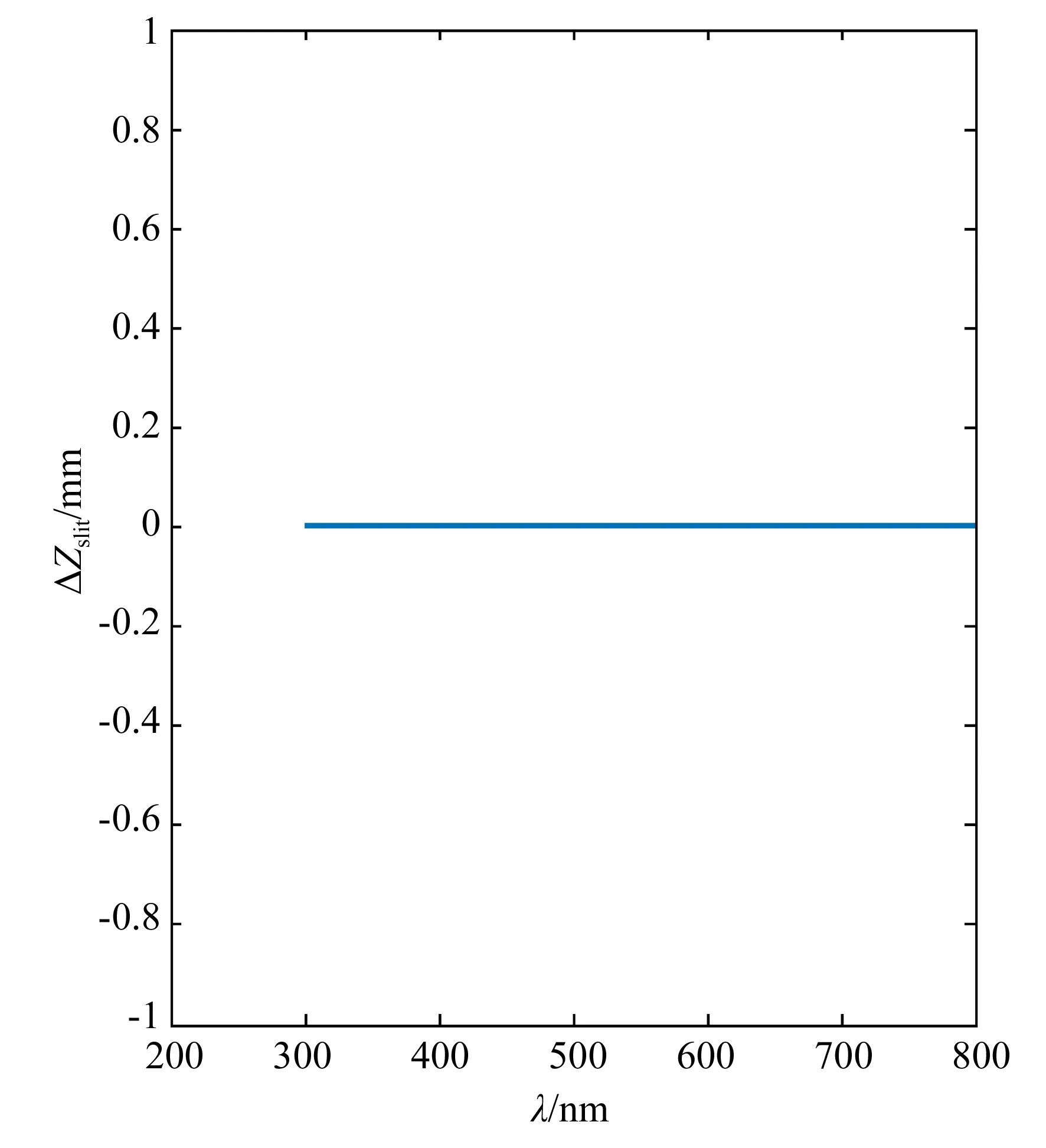
图10 不同波长、不同视场处的色畸变Fig.10 Keystone at different wavelengths and fields of view
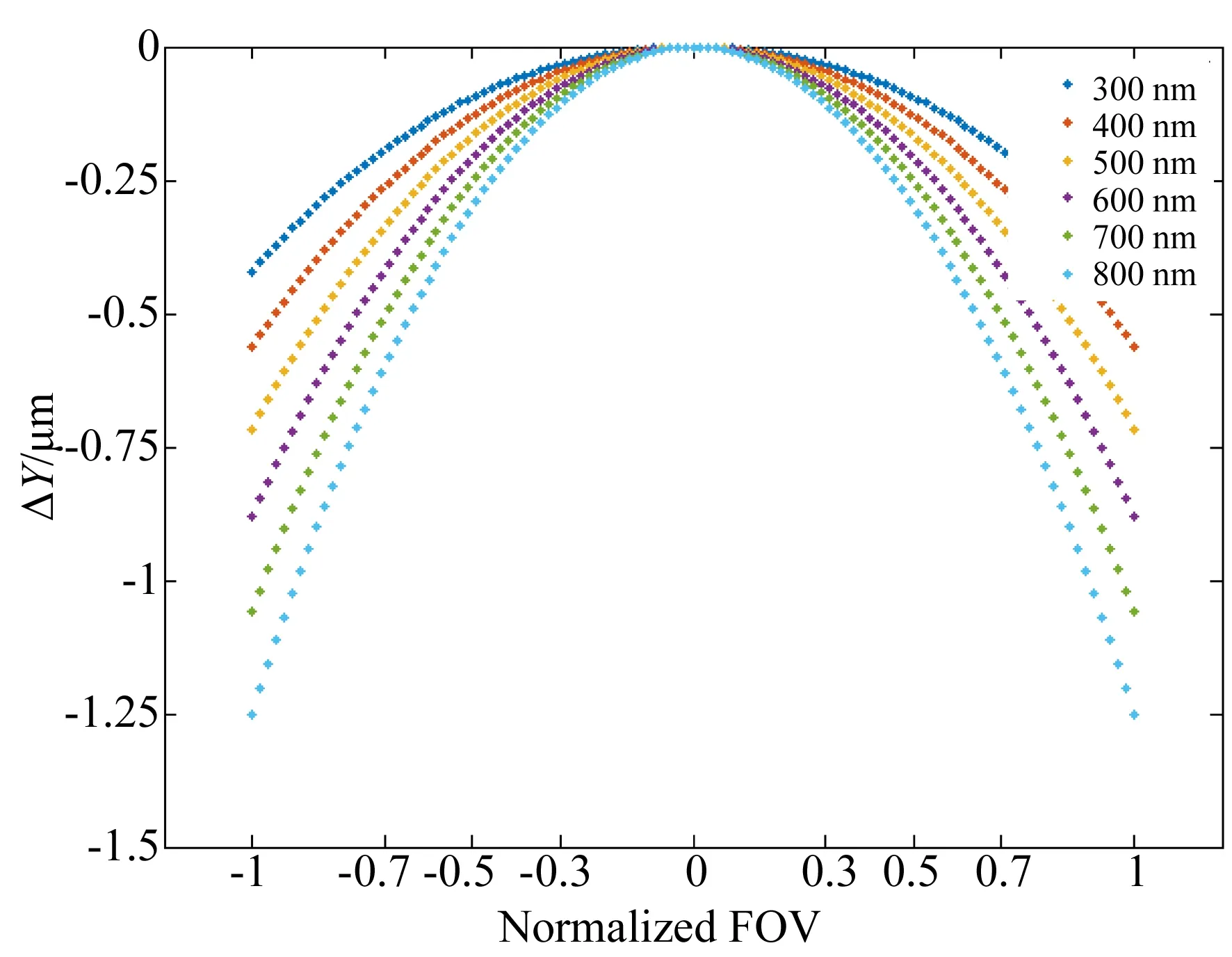
图11 不同波长、不同视场处的谱线弯曲变化曲线Fig.11 Curves of smile at different wavelengths and fields of view
其中横轴为系统的归一化视场,纵轴为实际的狭缝像相对理想像的中心偏移量,系统的最大谱线弯曲量约为1.25 μm。当系统选用探测器的尺寸为14 μm时,它远小于半个像元。在奈奎斯特频率为35 lp/mm时,不同波长处各视场的调制传递函数(Modulation Transfer Function,MTF)如图12所示,系统的MTF值大于0.7,成像质量优良。
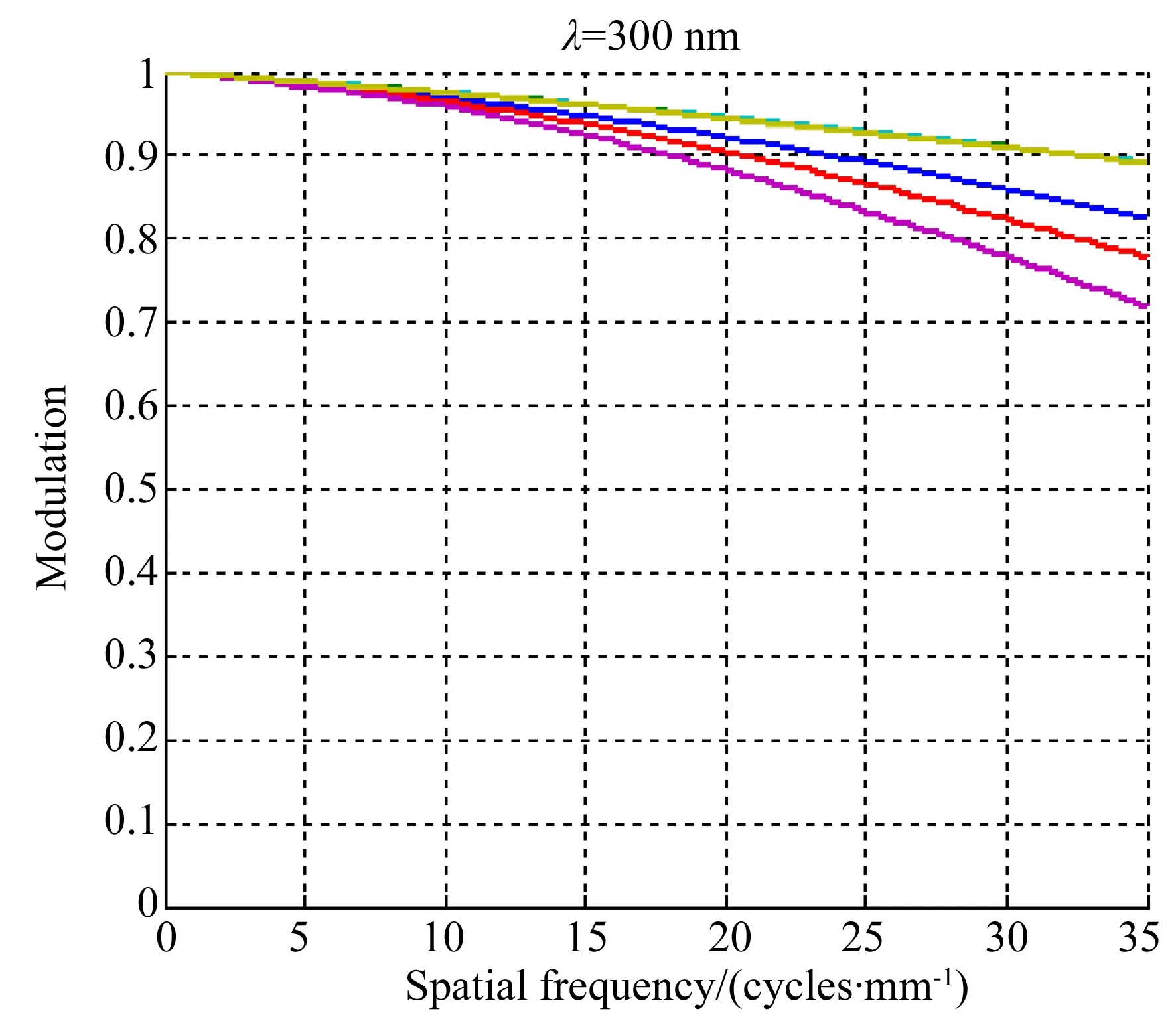
图12 系统在不同波长处的调制传递函数Fig.12 MTFs of system at different wavelengths
基于文中的系统结构,分别采用等间距的凸面光栅与变间距凸面光栅作为系统的分光元件,系统对应全波段内不同视场处的光谱像展宽变化曲线如图13所示。其中,横轴为系统的使用波长,纵轴为狭缝经过系统后的光谱像宽,显然变间距光栅的引入使得光谱像半高宽在光斑尺寸附近收敛,可以更好地实现全波段内光谱像的聚焦成像。
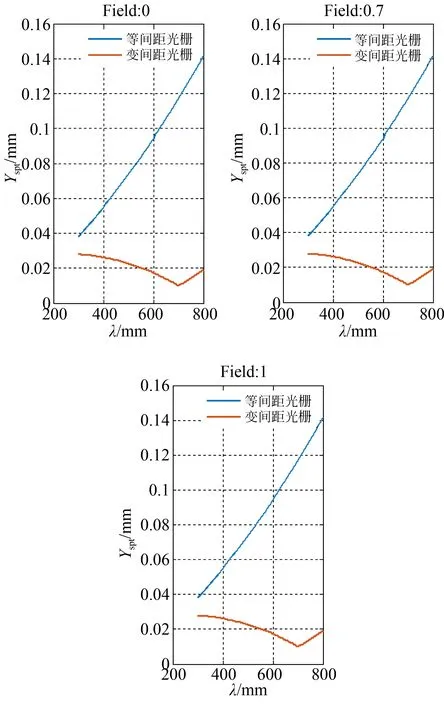
图13 不同视场处的光谱像展宽变化曲线Fig.13 Curves of spectral image broadening at different fields of view
4 结 论
本文提出了一种基于变间距凸面光栅的凸面光栅成像光谱系统的消像散设计方法。 对凸面光栅成像光谱系统的几何像差理论和聚焦情况进行分析,得出近轴光线的像散与凸面光栅刻线函数的关系式。并根据该关系式对凸面光栅的刻线型进行数值拟合,得到变间距凸面光栅的数值解,将设计波长处的像散优化到0.025 μm,实现了全波段内像散的均衡。本文设计的消像散凸面光栅成像光谱系统结构简单,易加工、装调,且相对孔径大、成像质量好,整体光谱分辨力在系统F数为2.7时优于3.3 nm,系统的极限分辨力为1.9 nm,可实现约201个高光谱通道,且系统在全波段内的光学传递函数值优于0.7,满足系统要求,对轻小型、高光谱的消像差凸面光栅成像光谱仪的研究具有重要意义。
