离焦像边界对曲率传感精度影响研究

肖春生，安其昌

(1.中国人民解放军91550部队，辽宁 大连 116023;2.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

1 引 言

大口径大视场望远镜在近二十年来发展获得了飞速发展，为了获得更高的巡天效率与集光能力，其口径与视场都在不断扩大[1-3]。国外已经研制并成功运行多台大口径大视场望远镜，8米级的大视场望远镜已经投入建设[4-5]，而国内尚未开展2.5米以上的大视场望远镜研究，与国际先进水平相比，不论是在占领“太空高地”保障国土安全方面，还是在探测存在撞击威胁的小行星等天文学邻域，均存在较大差距。为了进一步提升大口径大视场望远镜的探测能力，通过主动光学对望远镜中的各个主要部件进行独立、实时的面形校正与姿态控制，不仅可以降低对光学加工、系统装配精度的要求，还可以有效地放宽对大型跟踪架刚度的要求，降低系统运动惯量[6-7]，最终实现更好的成像效果。与以往以查表为主的主动光学系统相比，大口径大视场望远镜闭环主动光学系统具有校正频率高及可调自由度多的特点[8]。结合大口径大视场望远镜本身轴外像差敏感度高、焦面空间紧张的特点，亟需一种不附加过多元件，且可以覆盖全部视场的焦面波前探测方法[9-10]。

目前，大口径望远镜波前传感主要分为两类，分别为光瞳面波前传感(探测器与入瞳共轭)包括哈特曼传感器以及干涉仪，另一种探测方式为焦平面波前传感，利用焦平面所获得的图像，对波前进行恢复，这类技术被统称为“相位恢复技术”(Phase Retrieval, PR),包括曲率传感器，相位差异(Phase Diversity，PD)等。曲率传感技术在近年来运行的大口径大视场望远镜上，均有成功应用[11]。针对大口径大视场望远镜闭环主动光学系统，在传统曲率传感的基础上，通过多视场波前曲率传感，对系统高阶像差进行探测并在此基础上对系统中众多主动环节进行驱动。

对于常规的高分辨成像望远镜而言，成像视场往往不足1角分，其主动光学系统仅需要一颗导星进行波前传感，其像元分辨率很高，星点像边缘像素的影响往往可以忽略不计，同时，由于哈特曼传感器本身的特点，子孔径内的平均也降低了边缘像素的影响。因此，在本文曲率传感解算过程中，对离焦星点像边缘区域对波前解算的影响进行分析，分别从理论解和数值仿真的角度建立了边界信号与解算结果之间的联系。

2 曲率传感基本原理

曲率传感器由Roddier在1988年提出[11]，其基本原理是光瞳处波前局部的曲率变化，所对应的焦内像与焦外像的光强分布会发生对应的变化，如图1所示。根据近场电磁波的传输方程，可以解算出波前信息，如式(1)所示：

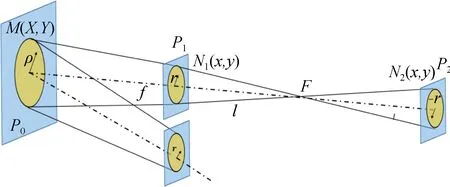
图1 曲率传感原理Fig.1 Principle of curvature sensing

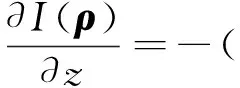
(1)

其中：I(ρ)为强度，Φ(ρ)为相位，为梯度算子，得到的结果为斜率，2为拉普拉斯算子，得到的结果为曲率。ρ为光瞳内坐标，z为光轴方向。由式(1)可知，解算的结果与波前的斜率曲率均有关。

对于自适应光学系统，一般离焦量仅为几个焦深，离焦星点像十分接近光瞳形状，相减后，可以认为：

δ(|ρ|-R)·Φ(ρ)→0，

故式(1)通过近似可得式(2)：

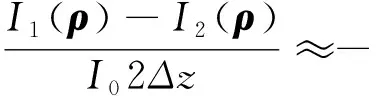
(2)

其中Δz为P1P2共轭位置相对入瞳的距离，如式(3)所示：

Δz=f(f-l)/l,

(3)

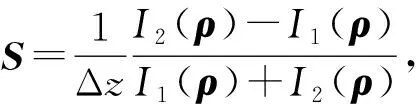
S=2Φ(ρ).

(4)

对式(4)进行泊松方程的求解即可，具体来说，通过光轴方向差分所估计的波前曲率建立式(4)。具体产生离焦像的方法可采用分光镜或者利用透明介质进行光程延迟。对式(4)两端同时进行傅里叶变换，可得式(5):

FFT(S)=FFT(2Φ(ρ))=

-4π2(u2+v2)FFT(Φ(ρ)),

(5)

其中u，v为空间频率。利用逆傅里叶变换，可得式(6)，基于式(6)即可获得曲率传感结果。

(6)

但是，对于大口径大视场主动光学，其离焦量可达到几百个焦深，因此，离焦星点像在像散的影响下椭率会非常大，相减之后，边缘区域面积相对增加许多，对于求解泊松方程的精度造成影响。

3 连续边界分析

实际处理中，由于边缘所占区域会被带入核心区域一起计算，因此，从理论分析的角度，对边界对大口径大视场主动光学望远镜曲率传感的影响进行分析。

分别就中心区域曲率为零与不为零的两种情况为例。

首先，分析整体波前像散Φ5(x,y)斜率与曲率之间的关系，首先整体波前像散Φ5(x,y)如式(7)所示:

Φ5(x,y)=α5ρ2cos 2θ=α5ρ2(2cos2θ-1)=

2α5x2-α5(x2+y2),

(7)

其中α5为整体波前像散系数。

对应的斜率如式(8)所示：

(8)

结合式(1)可得边界处的斜率如式(9)所示：

δ(|ρ|-R)·

(9)

基于式(5)可得整体波前像散曲率如式(10)所示：

Φ5(x,y)=α5[x2-y2]=0.

(10)

同理，整体波前彗差Φ7(x,y)如式(11):

Φ7(x,y)=α7ρ3cosθ=2α7x(x2+y2),

(11)

其中：α7为整体波前彗差系数。其斜率如式(12)所示：

6α7x2-3α7(x2+y2).

(12)

其曲率如式(13)所示：

Φ7(x,y)=[2α7x(x2+y2)]=24α7(x+y).

(13)

以此类推，边缘斜率数据如图2所示。

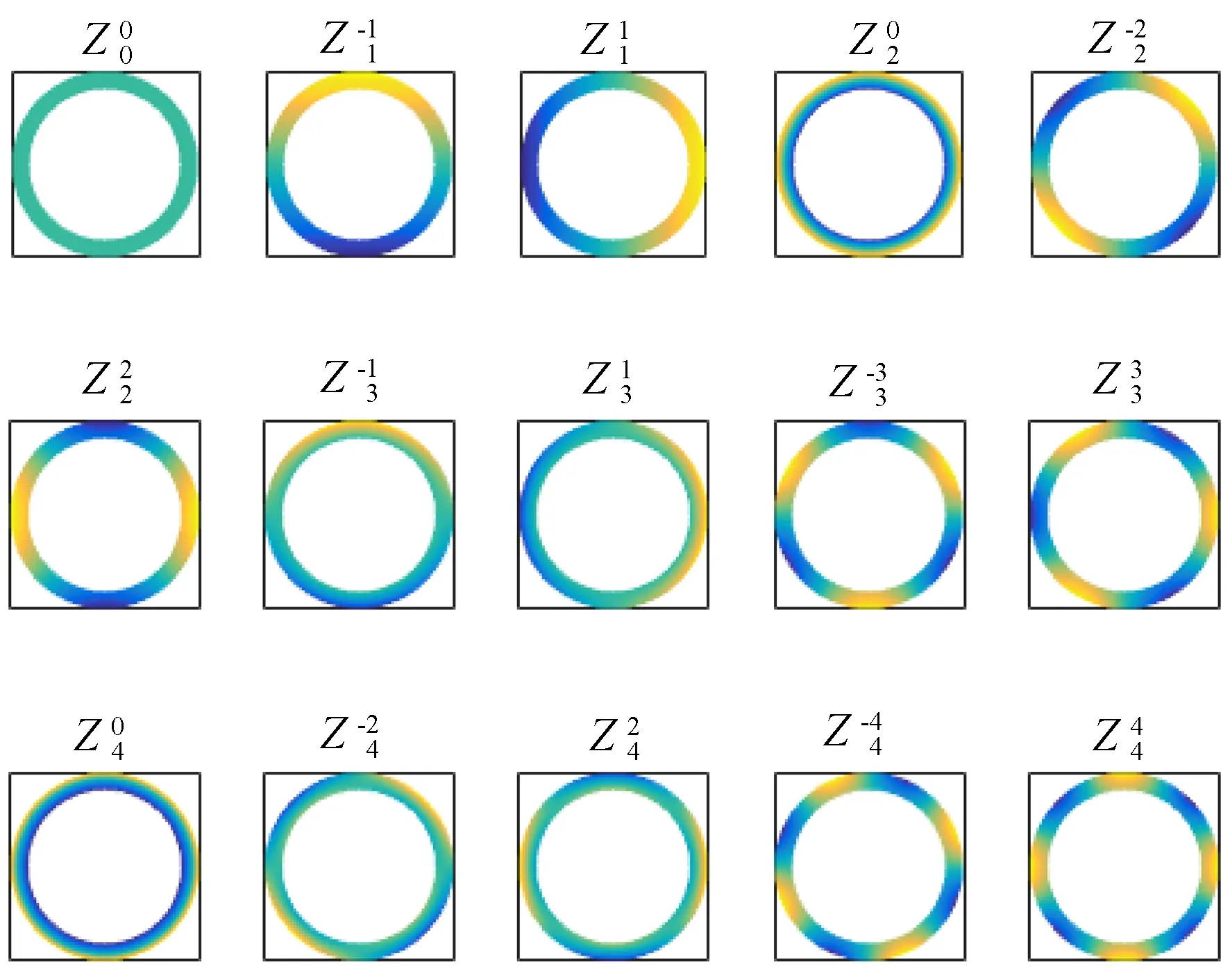
图2 边缘斜率数据Fig.2 Data of slope at wavefront edge

边缘所表现的为斜率信息，而按照曲率进行计算时，做差可以得到连续边界所引入的误差，如图3所示。

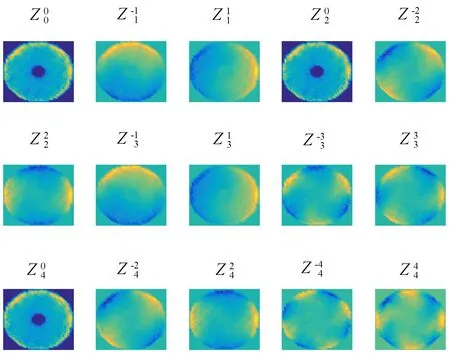
图3 边缘斜率带入的误差Fig.3 Error introduced by slope at edge

边缘斜率带入误差空间频域分布如图4所示。边缘处是斜率与曲率差别较大，同时由于没有进行迭代优化，边缘所造成的误差在空间频率较低时更加明显。

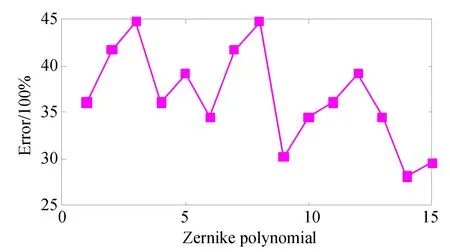
图4 边缘斜率带入误差空间频域分布Fig.4 Spatial frequency distribution of error introduced by edge slope

4 离散边界分析

离散情况，首先分析采样率影响，在此基础上，分析离散边界的影响。

元量化误差是星点探测的重要误差来源，同时也直接影响着波前传感精度。由于探测结果是以像元的形式表达，传统的ROI(Region of Interest)分析方法，基于高斯分布的星点像进行分析，通过阈值法获得星点像所对应区域[16]。而对于大口径大视场望远镜而言，其视场遮拦大，获取的离焦星点图为“DONUT”形式，同时，其不圆度随着视场的增大而增加，系统离焦星点像全宽半高DefFWHMCom与系统在焦星点像全宽半高focFWHMCom关系如式(12)所示。根据公式(12)可得，在焦像的FWHM大约为2″，最少占16个像元，离焦像为3.6″，至少51个像元。在此情况下，需要对元量化误差进行分析，探究目标星点的提取方法，获得元量化误差意义下最优离焦量。

(14)

其中:D为口径，l为离焦量，f为焦距。

由于大口径大视场望远镜，由于光学系统本身的畸变以及像差对应关系的非线性，导致传统的定标方法精度不足。针对天基大视场观测设备所获得的图像，拟采用分割视场的方法，将大视场分割为若干个小视场，在小视场中，对天光背景、光学系统固定像差以及图像畸变等进行分块研究，可以有效地降低拟合所需要的多项式阶数，减少边界处的拟合误差。对于离焦像的信息提取，与传统ROI技术不同，结合视场分割，使用局部的阈值，以便提取DONUT像。

那么针对理想系统，引入精度所对应误差，可得波前传感器所对应的检测误差，假设曲率传感离焦量为2 mm，前九阶Zernike多项式测量误差以30%计，假设每次都可以完全实现曲率传感所计算调整量，当要求测量误差小于5%时，迭代次数为3。因此，在粗对准环节后，通过“曲率传感—精调—曲率传感”的迭代循环，即可实现大口径大视场望远镜主动光学调节。

主焦点光学系统设计与仿真模型，如图5所示其设计视场为3°，取+1.45°处视场，利用曲率传感进行迭代的效果如图5所示，通过两步迭代其误差，将误差有效抑制。

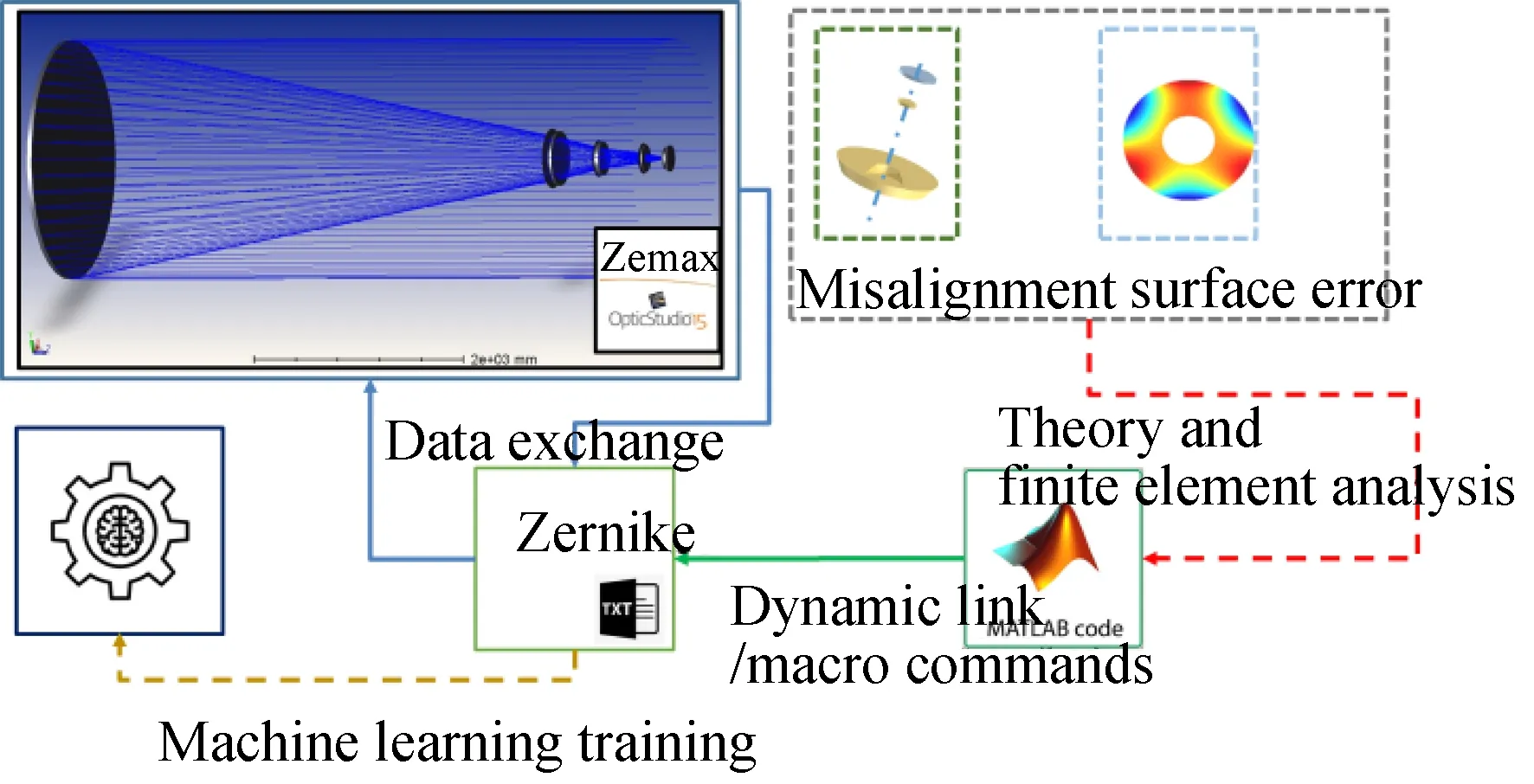
图5 主焦点光学系统设计与仿真模型Fig.5 Design and simulation model of primary focus optical system

主镜为600 mm球面镜，F数为4。后端共有4片校正镜，其中第1，2块透镜为双胶合透镜，用于校正部分色差。4块改正镜的口径分别为260 mm，160 mm，130 mm，126 mm。

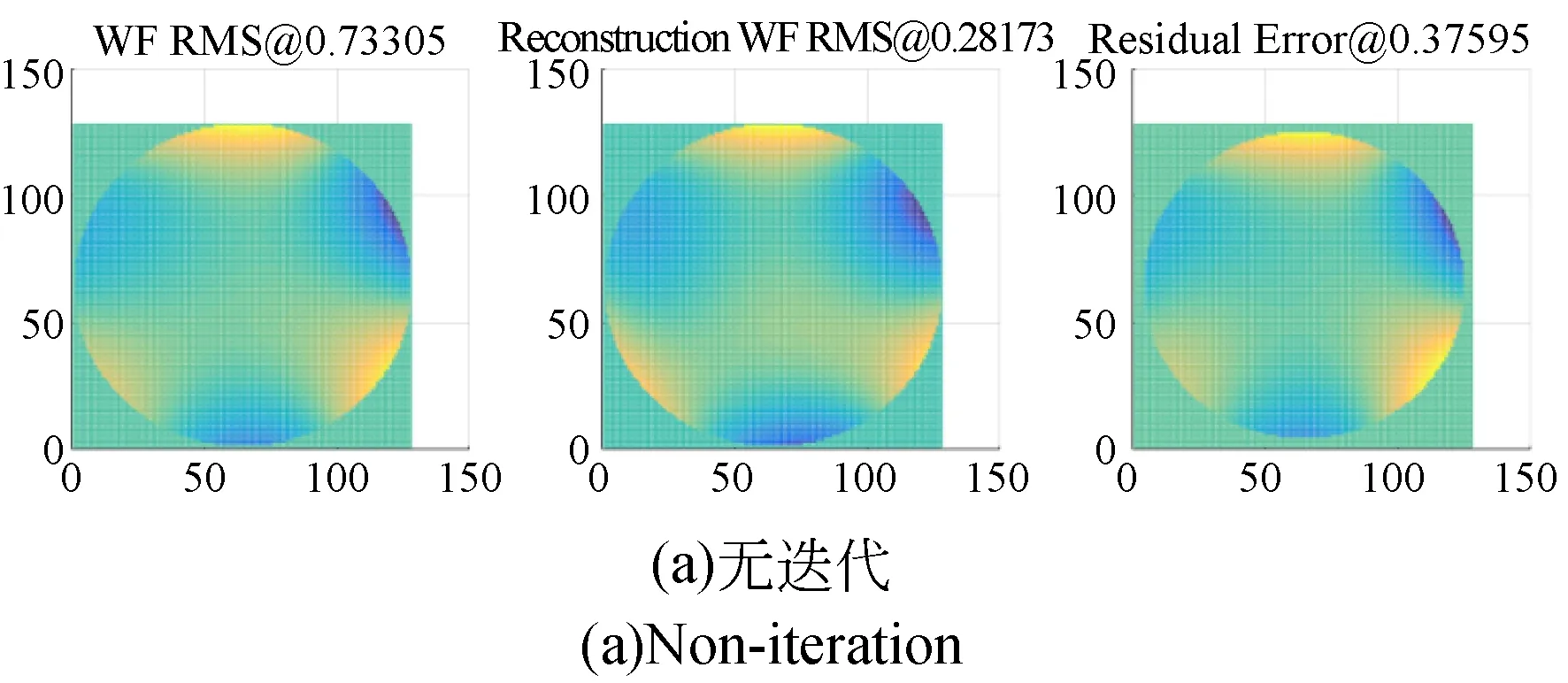
图6 曲率传感波前重建与迭代精度分析Fig.6 Curvature sensing wavefront construction and iteration analyses

在此采用阈值法从探测结果中提取目标图像。光学仿真软件与中值滤波模拟像元合并的过程，如图5所示，可见四叶梁对离焦星点像的影响在元化后可以忽略不计，同时边界像素数量下降很快，基本符合指数规律。单个星点像所对应的下采样图形，对于所对应的采样方式，其形态学所含有的信息差异已经较小，处于较为平缓的部分，不会由于形态学的变化，引起测量精度的大范围波动。

利用模型进行光线追迹得到离焦星点像，对边缘像素数量与下采用率之前的关系进行分析如图所示：其信息熵的变化[17]如图7所示，可见当采样率低于10×10后，其携带信息的能力迅速下降。

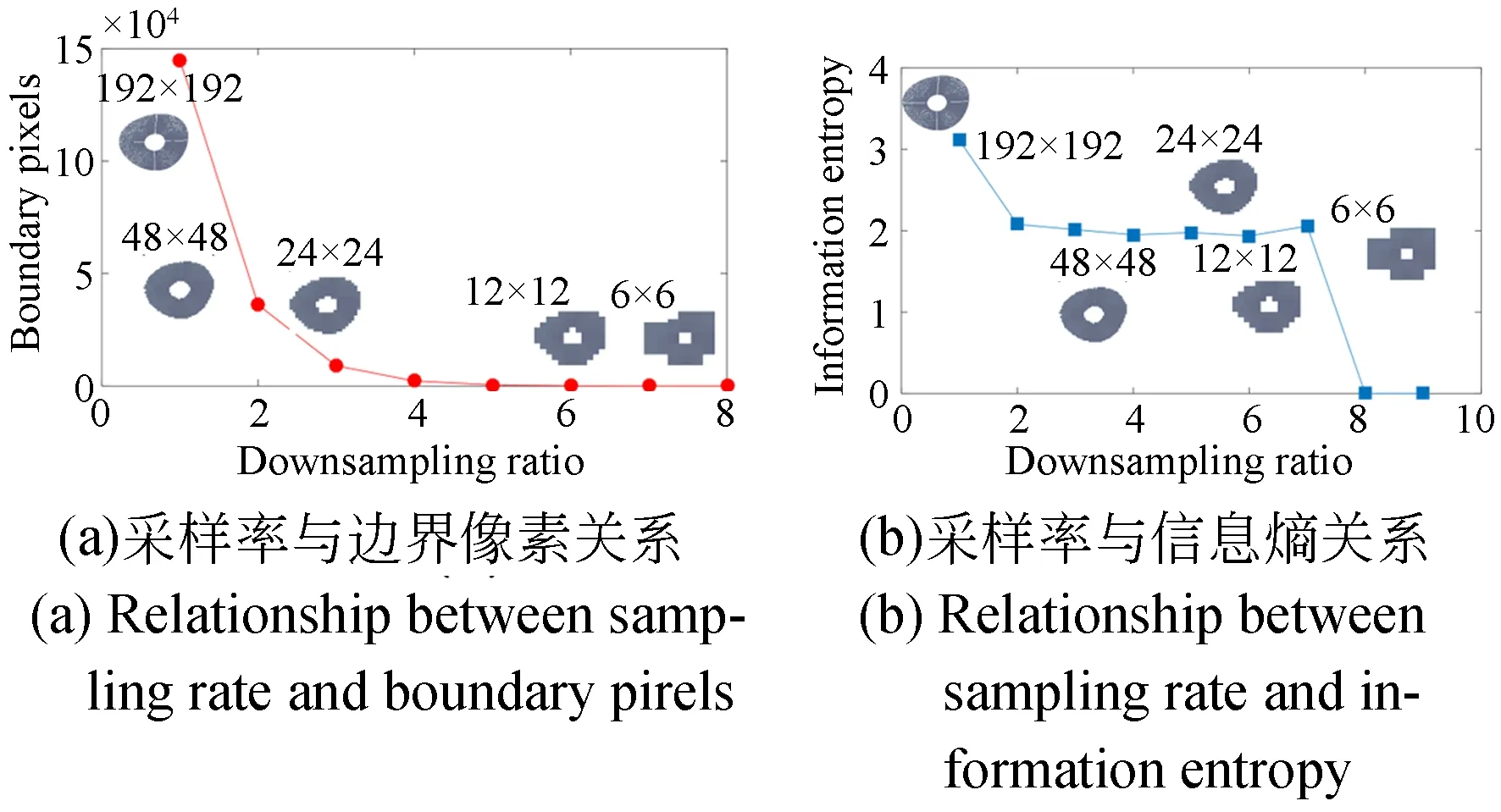
图7 星点像下采样Fig.7 Under sampled donut

对不同的采样率下的离焦星点像边缘进行解算，可得，在较低的采样率下，由于边界所占据的额像元数减少，其误差传播效应降低。针对彗差而言，减少了14%以上。

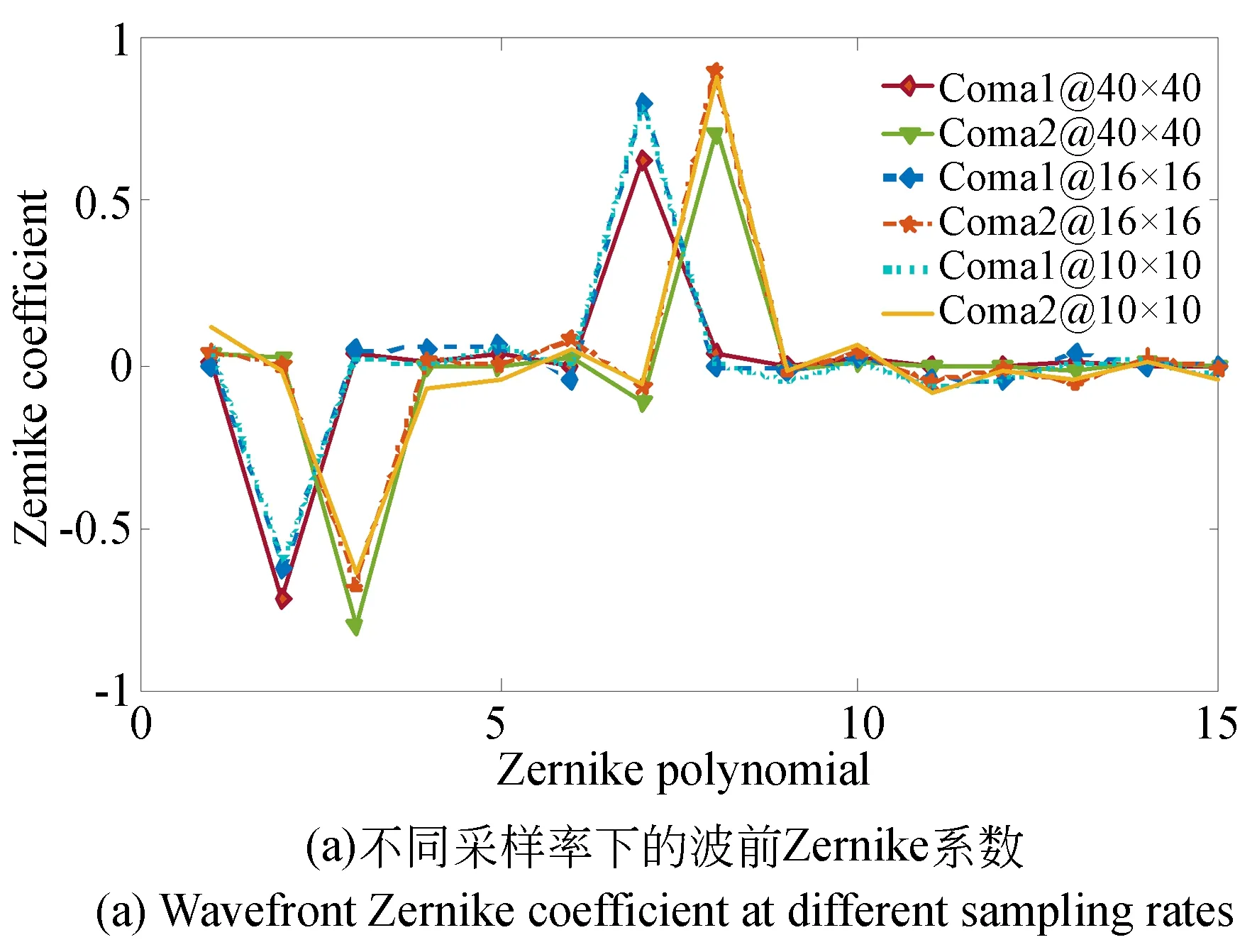
图8 星点像下采样Fig.8 Under sampled donut

利用单透镜可以对大口径大视场系统进行模拟与分析，采用的系统F数为4，其焦前焦后的探测所得的光强分布如图9(a)、(b)所示，通过光轴方向差分所估计的波前曲率如图9(c)所示。利用式(6)可得波前如图9(d)所示。实验现场如图9(e)所示。在不同采样率(40×40与16×16)下，彗差总体变化20%，与仿真结果吻合。可见，采样率的变化会影响波前像差解算的空间选择性，因此，需要更多的迭代步数获取结果。但是，过多的像元意味着离焦量较大，对探测信噪比会产生不利影响。

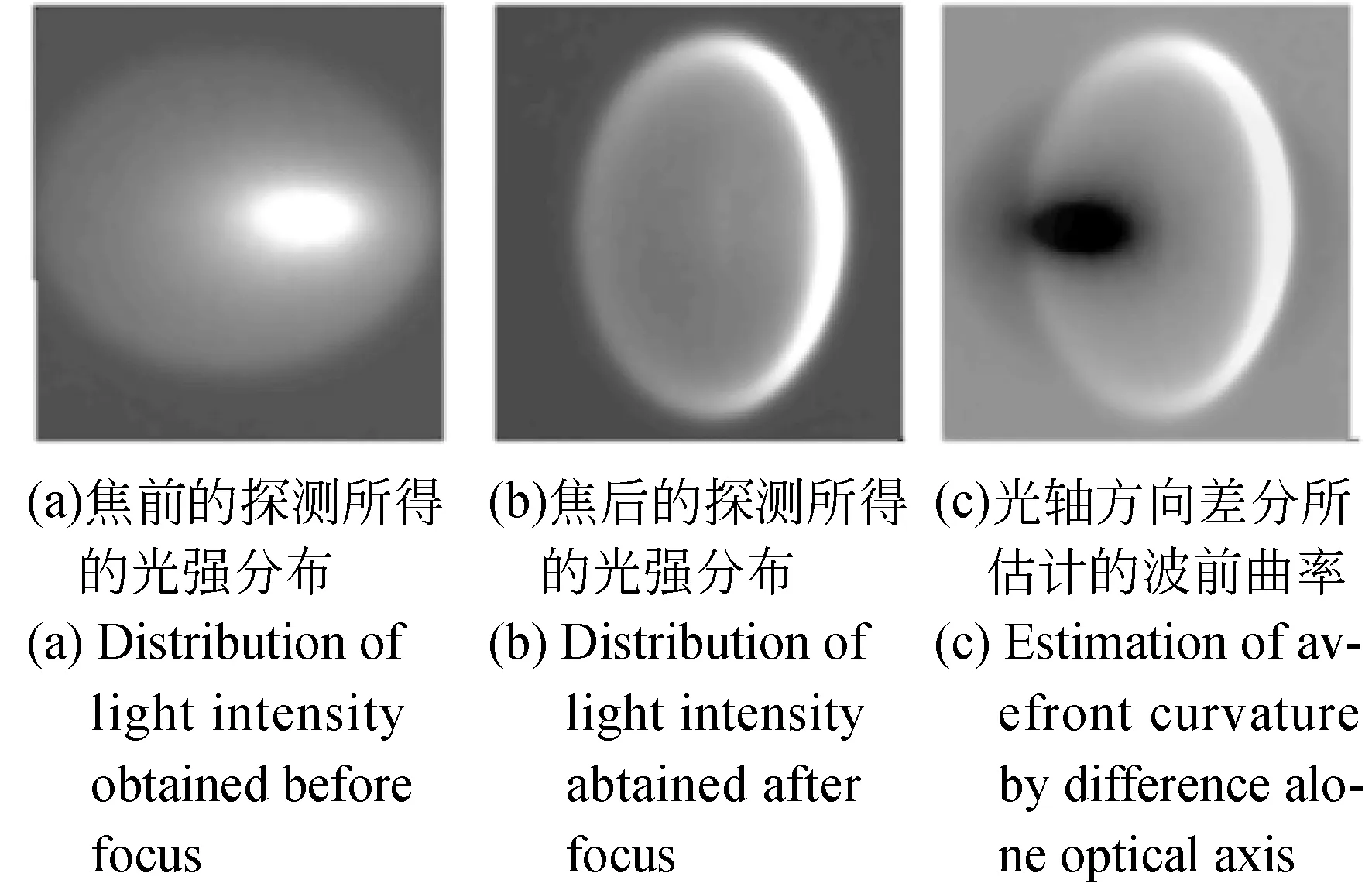
图9 波前曲率传感演示验证实验Fig.9 Domonstration of curvature sensing

5 结 论

实验结果表明：在连续情况下，单位圆边缘引入的误差约为0.5 μm；离焦星点像在100个像元以下，其携带信息的能力迅速下降；在接近100个像元时，对彗差的检测精度为0.035 mm，与400个像元时下降14%以上。

因此，在采样率较低的情况下，考虑闭环主动光学的误差收敛效应，通过两次迭代，即可将误差控制在30 nm以内，基本满足主动光学波前传感需要。如果需要得到更高精度或者更高空间分辨率，则需要悬着像元较小的探测器，根据斜率与曲率不同的数值特征，严格区分作用区域，进而分别进行求解。