基于励磁位姿控制的机械球关节系统控制策略研究
2020-11-24陈健杨丽荣巫丽萍
陈健, 杨丽荣, 巫丽萍
(江西理工大学,江西 赣州341000)
0 引 言
随着电力电子技术和传感器技术的发展,机器人领域正处于空前的发展繁荣期,发那科、ABB、嘉腾电子、川崎等机器人公司层出不穷,就目前而言,波士顿公司旗下的机器人产品技术相对成熟,不管是其结构还是智能化程度,都会更加贴近机器“人”的概念。但在现有的机器人学中,多是对现有的机器人结构进行分析研究,包括静力学和动力学建模、智能控制系统的设计及空间轨迹规划等,而对于机器人的关节结构设计及其优化控制策略却鲜有研究文章。
由于旋转电动机的技术相对成熟,在目前的工业生产中广泛使用的是臂式机器人(或称机械臂),绝大多数采用的是传统的电动机驱动的旋转关节。但不可否认的是,利用电动机驱动的不足之处在于电动机驱动系统体量较大,功重比较低;同时也会使机械臂的机动度受到一定制约,通常只能依靠串联更多的关节以提高机动度,致使系统的运动误差增大、驱动控制难度上升,为后期的机械臂动力学研究带来不便。对于仿生机械的设计,王晓磊等[1]提出了串并混联机构,杨龙等[2]提出了并联踝关节机构,金国光等[3]给出了球面变胞仿生关节机构优化设计思路,但其设计结构相对复杂,不利于机器人的小型化设计和运动控制。
本文以机器人关节结构的创新设计为出发点,借鉴文献[4]给出的3自由度球形关节电动机的研究成果,研究基于励磁位姿控制的机械球关节系统的控制策略。球关节结构在文献[5]中已有相关专利,并且在一些机械手腕关节设计中已得到运用,本文在此基础上结合励磁优化控制方式对球关节控制进行深入分析。
1 球关节系统结构
球关节系统由连杆A、连杆B和球关节组成,球关节系统结构如图2所示。连杆A连接在关节帽上,连杆B固连于球关节上,为避免产生涡流及磁场紊乱,关节帽和球关节可以采用非磁性材料,内部均匀分布有若干励磁线圈。夏鲲[6]给出的球形电动机模型,其结构如图1所示,在关节帽及球关节内部的每条球母线上均匀分布有若干励磁线圈。
球关节系统结构如图2所示。在图中建立一个笛卡尔坐标系,并固连于连杆A上,球关节绕X轴旋转时,使球关节内部励磁线圈通电顺序在YOZ平面内移动。同理,若需要实现球关节绕Y轴或Z轴旋转时,只需线圈通电顺序在ZOX或XOY平面内移动。同理,在球关节绕任意轴旋转一定角度时,仅需要将旋转动作进行分解,从而转化为绕X、Y、Z轴的旋转量。
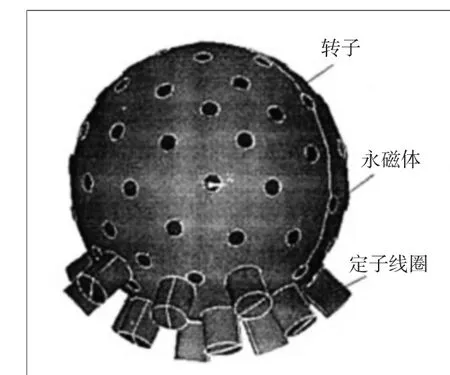
图1 球形电动机线圈布置图
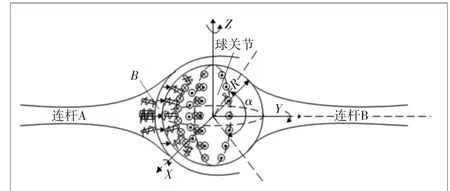
图2 球关节系统结构图
对于空间内任意的机械结构,其自由度可由修正后的CGK公式(Dai et al,2006)计算:
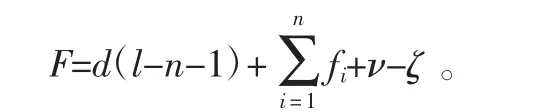
式中:d为机构的阶数,对于空间机构d=6;l为连杆数(包括基座);n为关节总数;fi为第i个关节的自由度数;ν为机构的虚约束数;ζ为局部自由度数。
根据计算,球关节共有3个自由度,即绕Y轴旋转360°,由于绕X、Z轴旋转方向存在行程约束,即可以分别绕X、Z轴旋转α角。而空间中机器人达到任意位姿所需要的自由度为6,只需要将2个球关节串联即可实现,这就证实了球关节结构可以增加自由度,提高机器人的灵活性。
2 球关节结构的运动动力学分析
2.1 球关节驱动力求解
励磁位姿控制是利用电磁吸附原理实现的,当两线圈通电时,若磁通方向相同,根据磁路最短原理,两线圈会相互吸引,改变其中一个通电线圈位置,则另一个线圈会跟随之运动,从而达到位姿控制的目的。

对于一个通电线圈,其磁通量Φ可由下式近似计算:式中:n为各线圈沿杆A的分量矩阵;N为线圈匝数;I为通入的电流;Le为有效磁通长度。
则此时球关节的通电线圈产生的电磁吸力为F,可以由下式近似计算:

式中,R为球关节半径。
因此,当球关节内部的线圈点阵按一定要求通以脉冲电流时,球关节就会随着脉冲电流的通电位置变化而发生传动,结合距离传感器的反馈信号获得关节位姿[7],从而实现励磁位姿控制。
2.2 球关节系统运动学建模
通常,对于传统的旋转、移动关节机器人的运动学模型,可以利用雅可比矩阵求解机器人的逆运动学方程,从而得到笛卡尔空间的位姿与关节空间的各关节角的映射关系。为了简化球关节的运动控制系统,考虑到球关节的运动可以分解为3个独立的旋转运动,将1个球关节等效为3个彼此邻近的转动关节,利用雅可比矩阵,建立基于球关节的逆运动学方程,得到笛卡尔空间下的位姿在关节球面上的映射关系。
为了方便分析,将球关节展开成一个平面内的圆形。根据球关节内侧由线圈构成的点阵分布,按一定的运动要求依次给线圈通电,形成移动磁场,如图3所示。
由控制器控制线圈通电位置往上移动距离x,移动速度为v,由于连杆A末端通电线圈固定,球关节将往反方向旋转相应的角度,根据弧长公式,可以得到关节旋转角与关节角速度θ˙。


图3 球关节平面展开图
对于球关节下的机器人运动学,本文将球关节近似等效为3个彼此邻近的转动关节进行分析,即对于2个球关节a、b串联而成的空间6自由度机器人,通过雅可比矩阵可以得到每一个笛卡尔空间位姿对应的关节空间姿态,即

式中:R为两球关节的半径;xa、va为a球关节的控制因子;xb、vb为b球关节的控制因子。
由此可以实现从笛卡尔空间到关节空间再到球坐标空间的转化,得到笛卡尔空间在关节球坐标空间的映射关系,从而得到驱动器的控制因子x和v。
3 步距角细分优化控制
由于现阶段的技术限制,无法在球关节有限的空间中布置大量的励磁线圈,因此关节控制的分辨率无法保证,根据文献[8]步进电动机细分驱动控制研究,步进电动机的控制方式多数采用了步距角细分原理,从而提高了运动精度。同理,在球关节运动控制中,也可以采用驱动器步距角细分来实现优化控制,提高关节运动的分辨率,其控制原理如图4所示。由控制器发出脉冲电流信号,通过改变脉冲数和脉冲频率分别控制关节转动角度和转速。结合预先设定的球关节运动方向,经过细分电路和功率放大,输出作为线圈点阵的驱动控制信号。

图4 步距角细分控制原理
当球关节内部线圈以全电流切换供电时,切换通电线圈,关节移动一步;若切换时不以全电流立即切换,而是进行半步切换,即切换前后两线圈均通入脉冲幅值相等的电流,则关节会移动半步,依此类推,脉冲细分工作如图5所示。
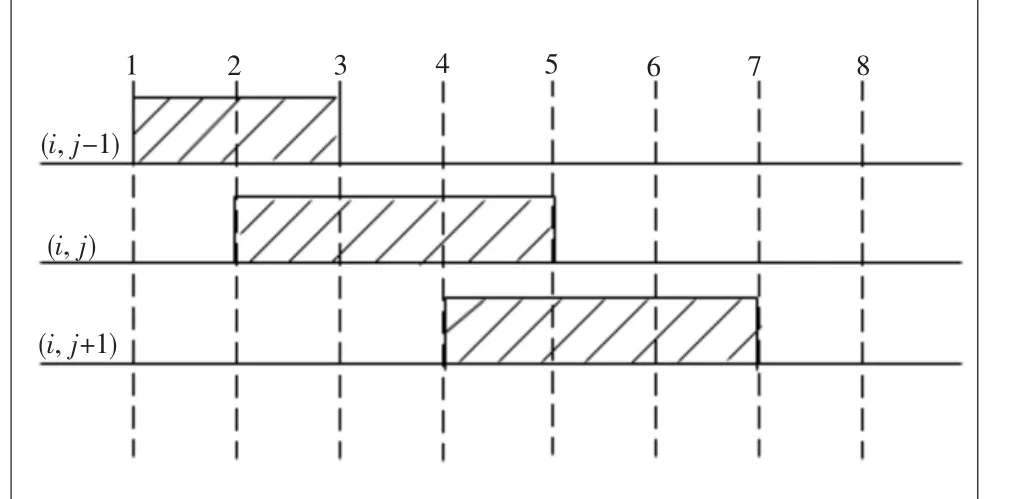
图5 脉冲细分工作图
图5中,(i, j-1)线圈先通电一个脉冲周期,然后(i, j-1)线圈和(i, j)线圈同时通电一个脉冲周期,再切换到(i,j)线圈通电一个脉冲周期,然后(i, j)线圈和(i, j+1)线圈同时通电,之后再切换到(i, j+1)线圈通电,依此类推。球关节由初始角转到终止角,从而实现球关节运动步距角细分优化控制。
4 结 论
采用励磁位姿控制的球关节结构设计可以解决传统关节的自由度不足的问题,提高机器人的机动性,有利于机器人的小型化。在机器人球关节控制中引入步距角细分的策略,可以改善关节的运动精度,提高运动平稳性。基于励磁位姿控制的机械球关节可以运用于仿生机器人设计、人机融合、医疗引导康复等,为机器拟人化设计提供了新的方案。但由于本文在进行运动学分析时将球关节结构近似等效为3个彼此相邻的转动关节,其运动学分析仍采用传统的雅可比矩阵的分析方法,具有一定的局限性,在后续的研究工作中可以进一步改进。
