窄深槽磨削加工过程的热分布研究
2020-11-24曹鹏飞梁国星郝新辉
曹鹏飞, 梁国星, 吕 明, 郝新辉
(太原理工大学机械与运载工程学院, 精密加工山西省重点实验室, 太原 030024)
窄深槽是指深宽比大于2且槽宽小于4 mm的一种特殊结构槽。在窄深槽加工过程中,大切深导致磨削接触区域弧长度比普通磨削大,砂轮的磨损和工件烧伤难以避免,研究窄深槽磨削过程中的温度分布情况是攻克这一问题的关键。
此外,砂轮和窄深槽侧面接触面积较大,摩擦磨损经常在磨削侧面接触区产生[1],所以不能忽略磨削区侧面的磨削换热情况。加工窄深槽时,由于材料去除率较快,使得磨削通常需要很高的比能,较大的比能和较快的去除率导致大量的热量产生,影响工件加工时的温度和工件表面质量精度。
在磨削温度的研究中,通常采用三角形热源模型进行分析[2-3]。郝新辉等[4]在电镀CBN(cubic boron nitride)砂轮对AISI 1045钢工件进行深切缓进给磨削试验的基础上,分析了窄深槽磨削过程中磨削温度的变化趋势,并针对窄深槽底部、圆角位置及槽侧面位置的温度分布进行了研究分析。Brosse等[5]在考虑到未变形磨屑形状和砂轮-工件接触的实际情况以及实际磨削实验得到的结果,三角形热源并不能最准确地拟合实际热源分布情况。王克军等[6]针对微磨削温度提出了超声振动辅助磨削的方法,有效地降低了磨削过程中的温度。王艳等[7]基于有限元法对热流密度热载荷进行离散加载,研究了抛物线热源模型及瑞利分布热源模型对平面浅磨磨削温度场分布的影响规律。Mohammadjafar等[8]通过对MQL(minimum quantity lubricant)平面磨削中多个散热因素的影响,建立了MQL状态下的磨削温度理论计算公式。郭国强等[9]建立了成型磨削温度的理论模型,对型面交界处最易产生磨削烧伤进行定量化分析。刘春利等[10]采用有限元仿真中的生死单元技术对窄深槽磨削温度场进行分析,结果表明,工件进给速度越大,仿真值越接近试验值。
现阶段研究磨削区温度的方式主要是将磨削区域作为一整体来研究,该方式在磨削深度较浅时较为合理。但当磨削深度较大时,尤其是窄深槽这种切深大、槽宽小的特有结构,其不同磨削区域都会产生相应的磨削温度场,且各个磨削区域的温度场相互影响明显,将窄深槽磨削区域的温度场作为一个整体来研究并不合理。现通过研究窄深槽加工过程中侧面磨削和底面磨削热流分布的差异,以及两个区域之间的温度分布相互影响效应,构建窄深槽磨削温度理论模型,并通过试验验证理论模型,以期为窄深槽加工工艺参数的优化提供依据。
1 窄深槽磨削区的热分布
1.1 窄深槽在顶刃区作用下的温度计算
窄深槽磨削过程中,可将砂轮参与磨削的部分分为顶刃区和侧刃区。顶刃区由砂轮顶端磨削刃与工件加工面相互作用产生,而侧刃区是由砂轮两侧面磨削刃对工件加工面磨削产生。加工成型槽底面时,槽底面只经过顶刃区作用。而槽侧面在磨削过程中先经过顶刃区磨削加工,再经侧刃区磨削。如图1所示,其中,A为槽侧面点,B为槽底面点。

图1 CBN砂轮及窄深槽结构Fig.1 CBN grinding wheel and narrow-deep-groove structure
在顶刃区磨削时,磨削深度较大,进给速度缓慢,砂轮顶刃和工件接触形成的磨削区近似为一段圆弧长。顶刃区的热流密度分布形状与加工材料的材料特性和加工工艺参数有关。工艺参数对顶刃区热流密度的影响主要由砂轮半径r与磨削深度ap决定。
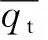
(1)

(2)
式(2)中:r为砂轮半径;a为形状系数。将式(2)用幂级数展开,可得:
(3)
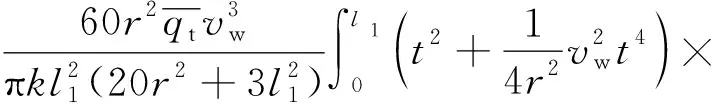
(4)
式(4)中:vw为工件进给速度;K0为零阶第二类修正贝塞尔函数;k为工件材料的热导率;t为磨削过程的某一时刻;z为任取磨削区一点的磨削深度方向值。
根据式(4)可计算得到砂轮顶刃作用于槽底时在顶刃区B点的温度TB1,以及侧面A点的温度TA1。此外,当侧面A点被砂轮顶刃磨削加工时,对应的磨削温度TA2及B点温度TB2也可由式(4)得到。
1.2 窄深槽在侧刃区作用下的温度计算
窄深槽在侧刃区磨削作用时,其加工过程中的磨削情况与端面浅磨相似。由于顶刃区的大切深磨削,在磨削区产生的大量能量作为热量进入到工件的加工槽附近,窄深槽两侧材料变软并且产生热膨胀效应,导致侧刃区材料去除厚度大于侧刃区的实际切深。当进给速度足够大时,过多的磨削热使砂轮侧刃区的热膨胀效应不可忽略,需要对侧刃区的磨削情况进行分析。
图2所示为窄深槽磨削过程的剖视图,其中DEF所表示的阴影面积为砂轮与工件接触的侧刃磨削区域Sc,可由极坐标表示为
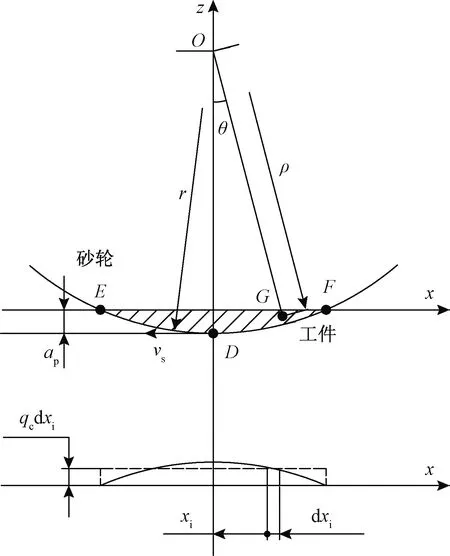
图2 窄深槽磨削中侧刃区几何模型Fig.2 Geometric model of the side blade section of narrow-deep-groove
(5)
式(5)中:ρ为侧刃区点O到任意一点G的矢径;ve为砂轮完全切入工件时整个侧刃区的平均磨削速率,计算公式为
(6)
则进入工件侧刃区的热流密度为
(7)
式(7)中:Ft为侧刃区切向力;ε为磨削区热分配比[11],计算式为
(8)
式(8)中:Aw为砂轮表面的磨粒破损率;γg为磨粒几何特性;ρ为密度;c为比热容;C为有效磨粒密度;下标c表示磨粒-磨削液复合体,w表示工件,g表示磨粒。将侧刃区看作是无数线热源的综合,这些线热源沿x方向以速度vw运动。每条线热源长短不一,当采用平均磨削速率ve时,每条线热源的单位热密度相等,定义线热源的平均长度热源为qcdxi,则磨削弧长为弦长EF。则侧刃区热源作用产生的温度场为

(9)
由式(9)可以算出窄深槽侧A点在砂轮侧刃磨削加工时的温度TA3及B点温度TB3。
在实际加工过程中,侧刃区磨削加工不仅需要考虑由热膨胀效应产生的小切深情况,还需要考虑其加工过程中受加工系统振动、砂轮表面磨粒尺寸及分布不均等因素的影响。加工窄深槽时的磨削深度很大,侧面磨削的单侧实际切深往往在200~500 μm,侧刃区切向力约为总切向力的1/5~1/10,窄深槽加工过程中需要充分考虑该区域磨削力情况,其产生的热量对于整个磨削过程的温度场分布影响不能忽略。
1.3 A和B点的理论温度
由式(4)计算得到B点在顶刃区热源作用下温度和工件材料的热传递系数hw1满足:
(10)
(11)
根据式(9)可知,在单个侧刃区磨削热单独作用下,B点的热源强度满足:
qB3=hw2TB3
(12)
(13)
式中:l2表示侧刃区弧长弦EF。在磨削热的多重作用下,即槽底顶刃区、槽侧顶刃区和两个侧刃区中产生的磨削热共同影响下,B点的热源强度为

(14)
由式(14)计算得到B点在磨削过程中的温升为
(15)
在磨削过程中,槽两侧磨削热的相互影响较小,可忽略不计,A点在磨削过程中的温升为
(16)
窄深槽磨削过程中,尽管槽底顶刃区、槽侧顶刃区和侧刃区的作用时间并不同步,但是其作用时间的前后间隔很短及应变率响应的温度滞后,磨削热在此过程中迭代累加并大量集中于磨削区表面,短时间而引起的磨削热变化不明显,所以在计算各点温度中采用了同一不同时刻产生的磨削热进行同步计算。
2 窄深槽磨削温度测量实验
实验采用单层电镀CBN砂轮缓进给磨削加工窄深槽,如图3所示。采用MV-40立式加工中心,主轴最高转速为10 000 r/min,使用的砂轮为单层电镀CBN砂轮,试验工件材料为40Cr钢。
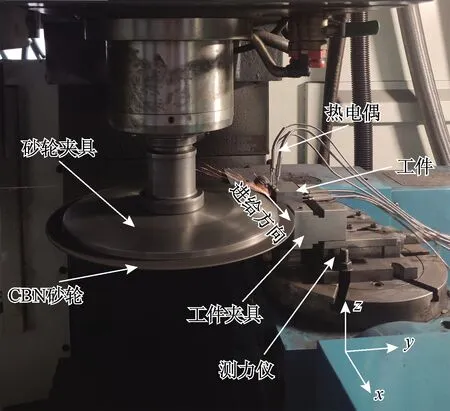
图3 磨削实验装置Fig.3 Grinding experimental device
磨削实验参数如表1所示,试验采用KISTLER9119AA2型测力仪测量磨削力,数据经该设备的采集处理系统处理后输入计算机,利用Dyno Ware软件对数据进行读取和存储。试验采用K型热电偶测量磨削温度,经标定后的K型热电偶具有良好的热-电动势线性关系,能较准确地测量-200~1 000 ℃内的温度。试验中的热电偶直径为1 mm,测量得到的温度数据信号由JY-5008D无纸记录仪采集。

表1 磨削实验参数Table 1 Grinding experiment parameters
热电偶同时测量窄深槽槽侧和槽底的温度,工件及热电偶孔位的截面位置如图4(a)所示,槽侧和
槽底的热电偶测温位置距离起始磨削端面共同设置为10、25、40 mm [图4(b)],其中测量侧刃区磨削温度的热电偶距离上表面2.5 mm,其理论深度为14.5 mm [图4(c)];测量顶刃区磨削温度的热电偶理论深度h为21.5、25.5、29.5 mm[图4(d)]。

图4 热电偶在实验中的测温位置Fig.4 Temperature measurement position of the thermocouple in the experiment
3 结果及讨论
图5所示为A点和B点的试验测温值与理论温度计算值的对比曲线。A、B两点在槽底顶刃区、槽侧顶刃区和侧刃区磨削热的多重作用下引起温升,尽管试验测温受到测温信号干扰和加工系统振动等的影响,温度测量值表现出一定的波动性,但不同磨削深度条件下的试验温度与相对应的理论温度虽然有差异,但总体上较为接近。如图5所示,在相同实验工艺条件下,位于槽侧A点的最高磨削温度高于槽底B点的最高磨削温度。这是由于A点位于槽侧顶刃区和侧刃区直接磨削作用面内,两个刃磨区的磨削热直接作用于A点,磨削热累积迭代引起A点温升,同时还有槽底顶刃区的磨削热通过热传导作用于A点。而槽底B点只受到槽底顶刃区的磨削热直接作用,同时槽侧顶刃区和侧刃区的磨削热通过热传导作用于B点,显然离A、B两点距离最近的磨削热源是引起两点温升的主要原因。
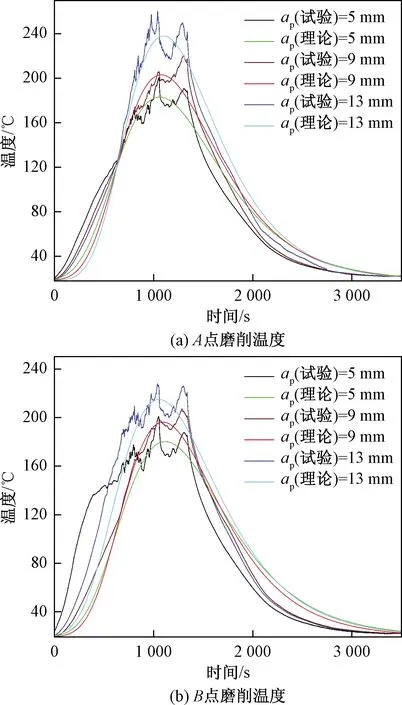
图5 不同切深时A、B两点的磨削温度Fig.5 Grinding temperature at points A and B at different grinding depths
而离A、B两点较远的热源通过热传导作用于两点,其在A、B两点产生的热流对两点的温升影响较小。当磨削深度为13 mm,进给速度为2.7 mm/min,在单独的槽底顶刃区磨削热作用及离B点较远的槽侧其他热源影响下,B点的处的温升不超过226 ℃,而A点在侧面两个刃磨区的磨削热耦合所用及槽底热源的影响下,最高温度接近260 ℃。所以在窄深槽磨削加工过程中,侧面受到的磨削热的影响最大。
在磨削深度为13 mm时,A点的试验温度测量值与理论计算数值的温度误差和相对误差如图6所示。试验测量温度值与理论计算值的平均相对误差为3.4%,在800~1 400 s阶段,部分磨削温度相对误差超过10%。这是由于磨削过程中的这一阶段磨削力较大,磨削温度攀升较快,测温信号干扰现象明显,此外加工系统受振动影响显著。其中93.4%的磨削测温值与理论计算值的相对误差小于10%,超过80%的试验温度与理论计算值相对误差小于7.5%。其他磨削条件下两者的相对误差与此基本一致。采用窄深槽磨削温度理论模型计算得到的窄深槽底面和侧面的磨削温度很好地反映了槽底面和侧面的实际温度情况,其结果可用于预测窄深槽磨削过程中槽底面和侧面的温度情况。由理论计算与试验测温可知,单层电镀CBN砂轮在缓进给磨削窄深槽工艺加工削过良好,窄深槽磨削温度的理论模型对预测磨削温度和工艺参数的选择有很好的参考价值。

图6 磨削温度误差Fig.6 Grinding temperature deviation
4 结论
研究了窄深槽顶刃区和侧刃区的热流密度分布情况,建立了窄深槽底和槽侧的磨削温度场模型,得到如下结论。
(1)在窄深槽加工过程中,顶刃区的热流服从圆弧形分布,侧刃区在磨削过程中服从端面浅磨 (切深为200~500 μm)。
(2)在磨削过程中,窄深槽底和槽侧受到多个磨削热的耦合作用,直接作用于加工面的磨削热源对加工面的温度影响最显著,不直接作用在加工面上的热源对加工面温度影响较小,但其产生的热量不可忽略。
(3)将试验测温结果与理论计算结果进行了比较,平均相对误差为3.4%,两者吻合较好,这表明窄深槽磨削温度理论模型能很好地反映槽底面和侧面的实际温度情况。
