高倍聚光光伏模组中菲涅尔透镜沿光轴方向的光照非均匀性变化及影响
2020-11-24江景祥舒碧芬崔高峻喻祖康杨云博
江景祥, 舒碧芬, 黄 妍, 崔高峻, 喻祖康, 施 琪, 杨云博
(中山大学太阳能系统研究所, 广东省光伏技术重点实验室, 广州 510006)
聚光光伏技术是太阳能发电的重要技术之一,目前采用菲涅尔透镜为聚光器的高倍聚光光伏(high-concentrating photovoltaic, HCPV)模组是重要的应用形式,通过光学聚光器件大幅度提升多结太阳电池表面的辐射功率,节省多结电池用量、降低成本,提高电池的光电输出特性。中外学者一直致力于提高多结太阳电池和模组效率,最新国际的多结电池和模组效率记录达47.1%、38.9%[1-3]。
多结电池具有很高的光电转换效率,但这仅在严格的实验条件下测试所得。实际应用中,当安装成模组进行户外使用时,模组效率要比多结电池效率低,其中一个原因是聚光光伏模组的输出特性不仅与光照能量有关,还与菲涅尔透镜的聚光特性有重要关系。目前在模组设计和应用中,多结电池通常放置于菲涅尔透镜的焦平面处,但聚光的非理想性使得多结电池处在非均匀光照的工作环境,降低多结电池的输出特性[4-6]。菲涅尔透镜的聚光光斑并非均匀分布,其能量分布形貌为高斯分布,电池中心区域承受高强度光照,降低了多结电池的光电转换效率[7-8],进而影响模组效率。因此在高倍聚光光伏模组的研究中,对光照非均匀性的改善,提高光学系统的聚光性能有重要的实际意义。
中外不少团队致力于优化光学系统、设计新型菲涅尔透镜等[9-12]。此外,改变菲涅尔透镜与多结电池的距离,聚光性能也会发生变化,使得模组输出性能随之变化。Steiner等[13-14]测试新开发的四结电池时,发现在聚光情况下,沿不同光轴位置电池的输出特性有波动。前期研究表明,多结电池放置在设计焦平面处,模组输出性能并非最佳[15-16],这是受到焦平面处光照高度非均匀和色散效应的影响。目前,中外对于沿光轴不同位置菲涅尔透镜光照非均匀性的研究还相对缺乏,为更好地研究沿光轴的非均匀性的变化情况,及其对模组输出性能的影响机理,以GaInP/GaInAs/Ge三结电池的高倍聚光模组为例,建立光学模型和三维三结电池网络模型,根据3个子电池的外量子效率(EQE)[17],把三结电池响应全波段(300~1 700 nm)分为短波段(300~700 nm)、中波段(700~900 nm)、长波段(900~1 700 nm),分析沿光轴非均匀性变化和模组电性变化,并把两者有机联系起来。最后对模拟的结果进行了户外实验验证。
1 数值计算模型
1.1 光学模型
为模拟沿光轴不同位置菲涅尔透镜的聚焦光斑的变化,进而分析沿光轴菲涅尔透镜的光照非均匀性,建立了等环宽、平板型菲涅尔透镜,设计参数如表1所示。由于500 nm的光线透过菲涅尔透镜任意齿环后,均聚焦到焦平面,因此不同齿环具有不同的侧面角。在光学模拟计算中,存在两种介质:菲涅耳透镜材料PMMA和空气。对PMMA而言,工艺上能做到基本均匀,并且在实际透镜的厚度下(3 mm),透镜材料的不均匀并不能造成可观测的散射,因而假定透镜介质是均匀的。对空气而言,在聚光光伏模组的尺寸下,光线在空气传播时不考虑空气折射。对光线通过菲涅尔透镜的过程,需要计算光线的出射轨迹和能量。图1为菲涅尔透镜聚焦的示意图,焦平面即为100 mm的光轴位置。
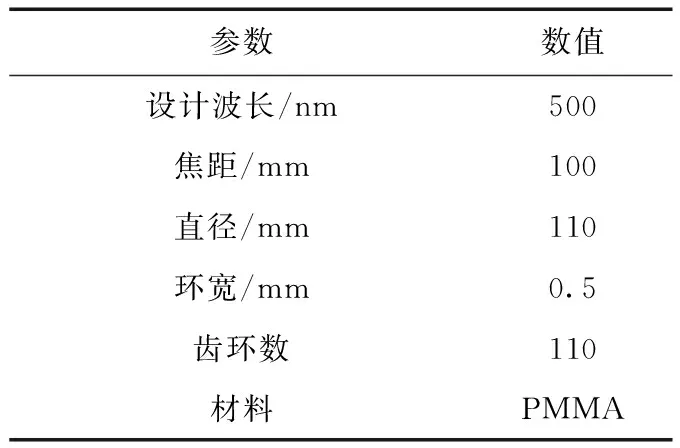
表1 菲涅尔透镜设计参数Table 1 Design parameters of Fresnel lens
光线出射轨迹的计算遵循折射定律,即入射角的正弦与折射角的正弦之比定于两种介质的相对折射率。在实际工况下,需要考虑光的色散现象,即太阳光不同波长的折射率不同,会导致通过菲涅尔透镜后的出射轨迹有所差异。图1表示了λ1、λ2两种波长的光线通过菲涅尔透镜的光线轨迹,光线垂直入射菲涅尔透镜后,在齿环发生折射,不同波长的光线通过菲涅尔透镜后照射在不同光轴位置。在计算中,空气折射率等于1,PMMA折射率根据Sellmeier方程确定[18],即
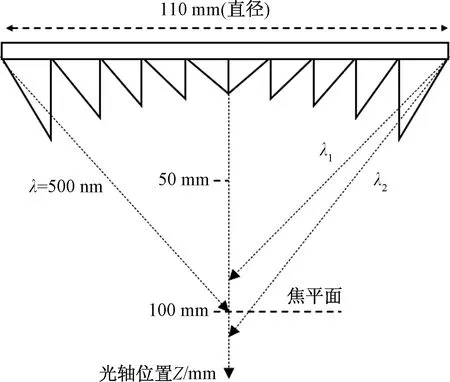
图1 菲涅尔透镜示意图Fig.1 Schematic illustrations of Fresnel lens
(1)
式(1)中:n为折射率;λ为波长,μm,B1、B2、B3、C1、C2、C3为PMMA 有关的常数,数据来自文献[18],如表2所示。
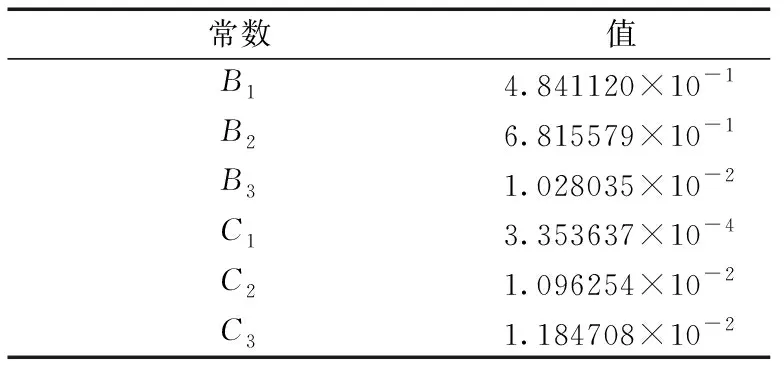
表2 PMMA的Sellmeier公式常数Table 2 Sellmeier formula constant of PMMA
光线能量改变的计算包括3个存在能量损耗的过程,3个过程在实际工况下同时出现,并且不可忽略:①光线垂直通过空气与PMMA的界面;②光线在PMMA材料中的传播;③光线再次通过PMMA与空气的界面,出射到空气中。对于过程②,考虑光线在PMMA材料中传播时对光的吸收,随着入射深度的增加,光线能量会减小,光线能量随入射深度的衰减情况符合朗伯比尔定律。而过程①、过程③涉及光线通过介质界面,结合波动光学的结论,通过菲涅尔公式[18]计算光线通过空气与菲涅尔透镜界面时的反射率和透射率。
上述关于光线出射轨迹和能量的计算均与波长相关,模拟计算的全波段范围为300~1 700 nm,其中每隔20 nm取一段小波段,以该小波段中间波长的折射率作为该小波段的折射率,该小波段的能量则根据太阳光谱积分求得。采用SMARTS模型来模拟太阳光谱,即阳光大气辐射传输模式[19](simple model for atmospheric transmission of sunshine),该模型考虑了太阳光在臭氧、水蒸气、混合气体的透射比,阳光经过的路径等,能很好地模拟太阳光谱曲线。
1.2 电路模型
在研究菲涅尔透镜的聚光特性的基础上,进一步研究沿光轴菲涅尔透镜聚光下三结电池的输出特性。通常而言,采用三结电池的双二极管模型,可求解均匀光照下电池在一定聚光倍数和温度下的电学特性,每个子电池用独立的电流源、双二极管、并联电阻表示,子电池之间通过隧道结串联,隧道结可用串联电阻表示。三结电池双二极管模型的计算方法为
(2)
式(2)中:ILt、ILm、ILb分别代表InGaP、InGaAs、Ge子电池的光生电流;I0t1、I0t2、I0m1、I0m2、I0b1、I0b2分别代表每个p-n结二极管的反向饱和电流;Vt、Vm、Vb分别代表各层二极管两端电压。
但在高倍聚光光伏模组实际工况下,三结电池承受非均匀光照,考虑到三结电池双二极管模型只能用于均匀光照的情况,当光照非均匀时,电池输出特性与均匀光照下的特性不同,这种不同并不能从等效电路中得到反映,故三结电池双二极管模型不适用于求解电池在非均匀光照下的电学特性。非均匀光照与均匀光照的不同在于是否考虑光照在电池表面的分布,在考虑光照分布的前提下,就不能把电池看成单一的电路元件。因此采用三维三结电池网络模型[20-21],该模型可看作对三结电池双二极管模型的扩展,更能表征三结电池的实际工作情况。模拟了尺寸为5 mm×5 mm的GaInP/GaInAs/Ge三结电池,表面被划分为小电池阵列,每个小电池具有和电池整体相近似的电学特性,小电池之间通过横向电阻连接,用独立的双二极管模型表示。电池表面除了接受太阳光的光照区域外,还有细栅区域和边缘的主栅区域,这些暗区域的小电池不接受光照,因此双二极管模型中不含电流源。三结电池结构及三维三结电池网络模型如图2所示。

图2 三结电池模型Fig.2 Models of the triple-junction solar cell
2 沿光轴光照非均匀性分析
在高倍聚光光伏模组应用中,菲涅尔透镜存在非理想性,聚焦光斑的能量形貌符合高斯分布,并且沿光轴不同位置,照射在电池表面的光照非均匀的程度有所差异。沿光轴进行非均匀性分析,对下一步研究沿光轴电池输出特性变化有重要意义。
菲涅尔透镜聚光光斑的非均匀性,通常可用峰均比(peak-to-average ratio,PAR)进行量化[22-23],其定义为光斑最高辐照度与平均辐照度的比值,由于光斑能量分布为高斯分布,因此最高辐照度出现在光斑中心位置。针对短、中、长波段和全波段,分析了沿光轴的辐射功率和峰均比(PAR)的变化,如图3所示。

图3 沿光轴短、中、长波段和全波段的辐射功率和峰均比(PAR)的变化Fig.3 Changes of radiation and peak-to-average ratio (PAR) of short, medium, long and full band along the optical axis
对辐射功率而言,当某个波段的光斑尺寸小于三结电池尺寸时,该波段的能量全部聚焦到电池表面,因此电池表面的辐射功率在沿光轴变化时,会在一个光轴区间内达到峰值,即图3辐射功率曲线平坦的区间。菲涅尔透镜色散效应的影响下,最大辐射功率的光轴区间逐渐后移,即向110 mm的光轴方向偏移。短、中、长波段的最大辐射功率区间有所不同,大致位于98.9~102.9 mm、100.1~104.9 mm和101.3~104.5 mm,全波段的最大辐射功率区间为100.4~103.1 mm,是短、中、长波段共同作用的结果。
对峰均比而言,在90~95 mm、105~110 mm的光轴区间,三波段均呈现较低的峰均比,说明在此光轴区间光照均匀性良好。在菲涅尔透镜焦平面附近,峰均比发生剧烈变化,说明光照非均匀性明显增强。相比于短、中波段,长波段内各小波段的折射率变化更小,因此长波段峰均比剧烈变化的光轴区间相对较窄。受色散效应的作用,短、中、长波段的最大峰均比以及所在的光轴位置各有不同,分别在101.2、101.8、102.9 mm有最大值,不同波段的最大峰均比及其所在的光轴位置如表3所示。比较辐射功率和峰均比曲线,电池表面的最大辐射功率的光轴区间依次向110 mm的方向偏移,因此最大峰均比所在的光轴位置也随之偏移。

表3 不同波段的最大峰均比(PAR)的光轴位置Table 3 The optical axis position of the maximum peak-to-average ratio (PAR) of different wavebands
全波段在102.1 mm处有最大峰均比56.0,焦平面处峰均比为34.5,这是短、中、长波段综合的结果。短、中波段的能量占全波段的比值大于50%,对峰均比影响的权重更高,因此全波段最大峰均比(56.0)更接近短、中波段的最大峰均比。此外,峰均比最大值出现的光轴位置应在短、长波段之间(101.2~102.9 mm),长波段内各个小波段的折射率变化更小,对峰均比最大值出现的光轴位置有更显著的影响,因此尽管长波段能量占比较低,全波段最大峰均比的光轴位置(102.1 mm)仍略微倾向长波段的最大峰均比位置。
就不同光轴位置的光照非均匀性而言,在102.1 mm附近光轴区间,菲涅尔透镜聚光非均匀性较强,远离该区间的光轴位置,反而有更良好的光斑。在实际工程应用中,三结电池通常放置于透镜焦平面处,输出特性受到非均匀光照的负面影响,改善电池放置的位置可有效提升光斑均匀性,提高三结电池和模组整体输出性能。
3 沿光轴光照非均匀性的影响机理
通常而言,三结电池短路电流主要受辐射功率和电池表面光谱分布的影响,开路电压随光照的变化较小,光照非均匀性主要通过影响填充因子,进而影响三结电池输出性能。对实际高倍聚光光伏模组,在菲涅尔透镜聚焦下,不同光轴位置三结电池表面光照非均匀程度的差异,将导致三结电池的填充因子随光轴位置发生变化,进而影响模组的输出性能。
图4所示为沿光轴不同位置,全波段峰均比和填充因子的变化,两者呈现明显的负相关关系。远离焦平面处峰均比较低,菲涅尔透镜的聚光均匀性良好,填充因子达到90%左右;随着光轴位置逐渐靠近焦平面,峰均比随之增大,光照非均匀性增强,填充因子逐渐下降,100.8~102.9 mm的光轴区间内最低,下降至约52%。
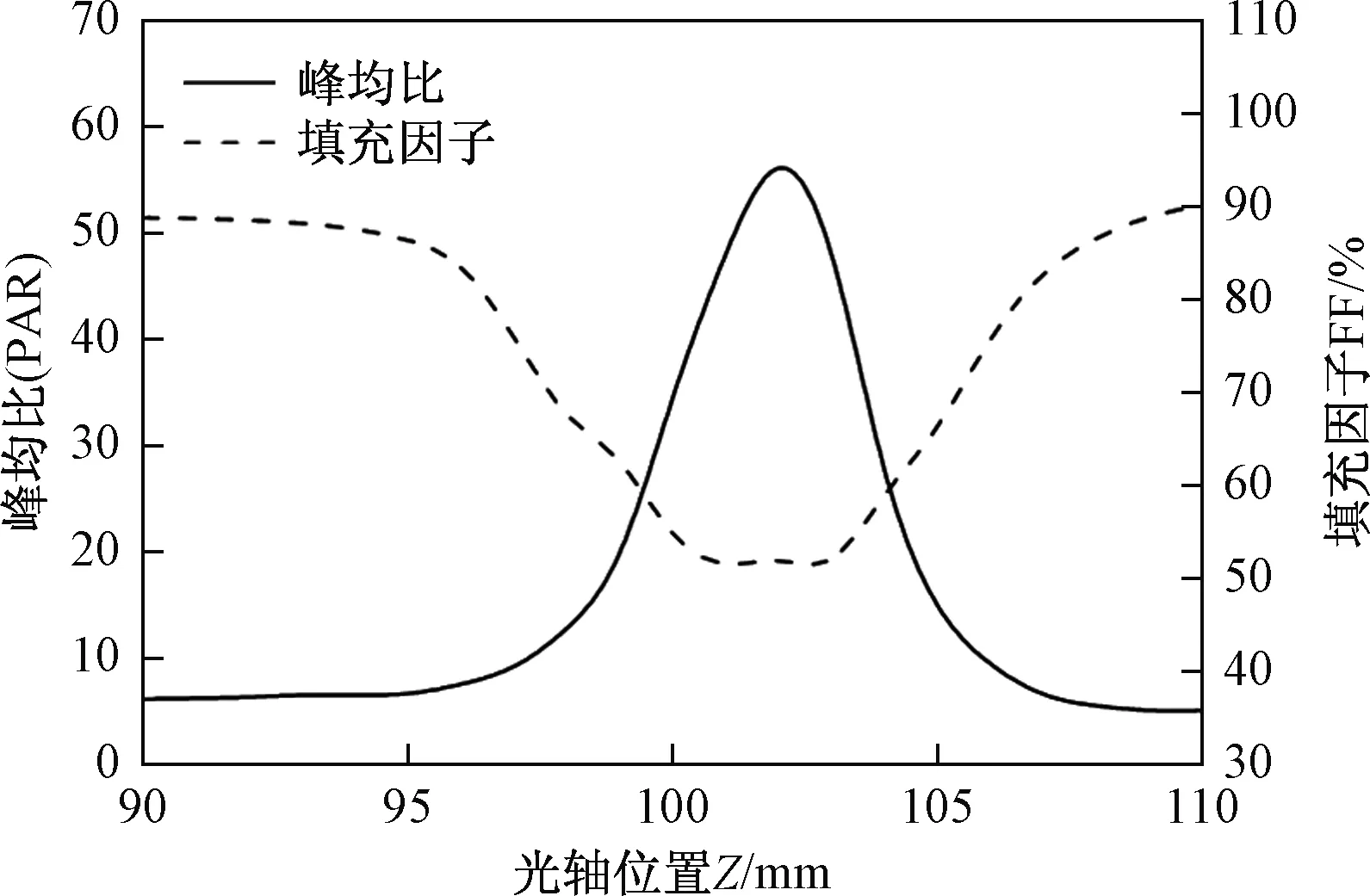
图4 沿光轴全波段峰均比和三结电池填充因子Fig.4 Peak-to-average ratio and filling factor of triple-junction solar cell along optical axis
图5表示了峰均比和填充因子两者的关系。峰均比小于20时,随着峰均比的增大,填充因子从90%迅速下降至62%,说明此时三结电池填充因子对光照非均匀性的敏感度较高,光照非均匀性刚开始发生恶化时,三结电池的电性发生急剧的变化;峰均比大于20时,随着峰均比的增大,填充因子的下降趋势减缓,峰均比达到50后,填充因子基本稳定在52%,说明光照非均匀性增强到一定程度后,三结电池电性变化逐渐减缓,最终达到稳定状态。

图5 峰均比与填充因子的关系Fig.5 Relationship between peak-to-average ratio and filling factor
填充因子的降低表明三结电池内部有效串联电阻的增加,而有效串联电阻与三结电池表面横向电流有密切关系。当三结电池处于均匀光照的情况下,三结电池表面光生电流处处相等,但在非均匀光照的情况下,光照更强的区域电流密度比其他区域更高。在菲涅尔透镜聚焦下,光斑辐照度分布形貌呈高斯分布,三结电池中心区域的电流会流向较暗的电池边缘区域,即产生横向电流,增加有效串联电阻,更高的电阻损耗产生了比电流匹配时更低的电池转换效率,三结电池整体呈现出填充因子下降。
图6表示了电池表面发射区沿栅线方向的横向电流分布,选取5个典型光轴位置(96、100、101、102、104 mm),电池尺寸0、2.5 mm分别表示电池中心和电池边缘。电池边缘区域光照辐照度梯度较低,局部区域产生的光生电流差异较低,横向电流约为0.10 mA;随着电池尺寸向电池中心靠近,光照辐照度梯度逐渐增大,横向电流逐渐增大;当电池尺寸位于电池中心附近区域,光照辐照度接近高斯分布的顶点,光照梯度迅速下降,横向电流迅速从最大值下降到0 mA。从图6能看出,沿光轴不同位置横向电流的大小有明显区别。在96 mm的光轴位置,横向电流在电池尺寸0.18 mm处达到最大值(0.57 mA);当光轴位置位于焦平面附近时横向电流较大,100、101、102 mm处横向电流最大值分别为1.53、1.99、1.73 mA;在104 mm处,横向电流回落,最大值为1.07 mA。

图6 不同光轴位置,三结电池发射区沿栅线方向的横向电流分布Fig.6 Transverse current distribution along the grid line in the emitter of triple-junction solar cell at different optical positions
结合上述填充因子、峰均比、横向电流的分析,可以看出填充因子与峰均比之间存在强负相关性,对菲涅尔透镜聚光下的高倍聚光光伏模组,沿光轴不同位置光照非均匀性有所差异。当三结电池位于102 mm附近,光照非均匀性较强,造成横向电流较大,电池效率随之降低,填充因子仅为52%左右;当三结电池远离102 mm时,光照均匀性得到改善,横向电流降低,填充因子显著提升,光轴位置为104 mm时,填充因子回升至59.0%,光轴位置为96 mm时,填充因子能达83.4%。
实际应用中,三结电池放置于焦平面处,虽然能获得较高的辐射功率,但填充因子位于低点,降低了模组整体输出性能。改变三结电池放置的光轴位置,能有效地提升填充因子。
4 实验研究
为了验证模拟的结果,进行户外高倍聚光光伏模组的输出特性测试。实验在广州市中山大学太阳能系统研究所楼顶进行,实验设备如图7所示,使用室外双轴跟踪平台进行追日跟踪,实验设备安装在跟踪平台上。采用尺寸5.0 mm×5.0 mm的三结电池,以及直径110 mm、焦距100 mm的菲涅尔透镜。测试的光轴范围在95.0~104.5 mm,步长为0.5 mm,共20个光轴位置。实验时辐照度为750~800 W/m2,环境温度为25 ℃,变动幅度在1 ℃以内。
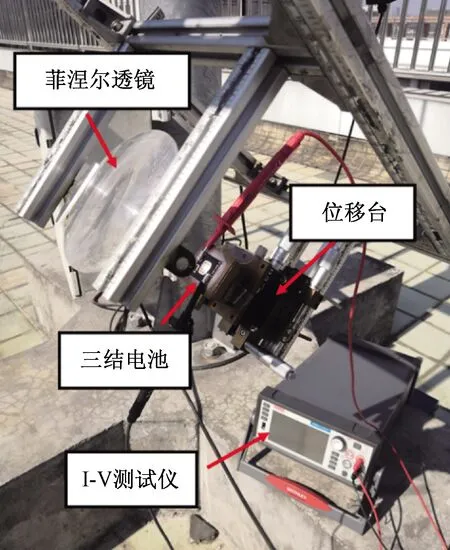
图7 户外模组测试的实验设备Fig.7 Experimental equipment for outdoor module testing
图8所示为沿光轴不同位置的填充因子和最大输出功率,数据为5次重复实验的平均值。沿光轴模组的输出性能不断发生变化,填充因子在焦平面处为65.7%,101 mm处有最小值63.7%,最大输出功率在焦平面处为0.78 W,最小值(0.75 W)在101 mm处。远离焦平面处填充因子约为70%,比最小值提升9.9%,最大输出功率在96、104 mm处有极大值,为0.87、0.91 W,相比焦平面处提升12.2%、16.8%。
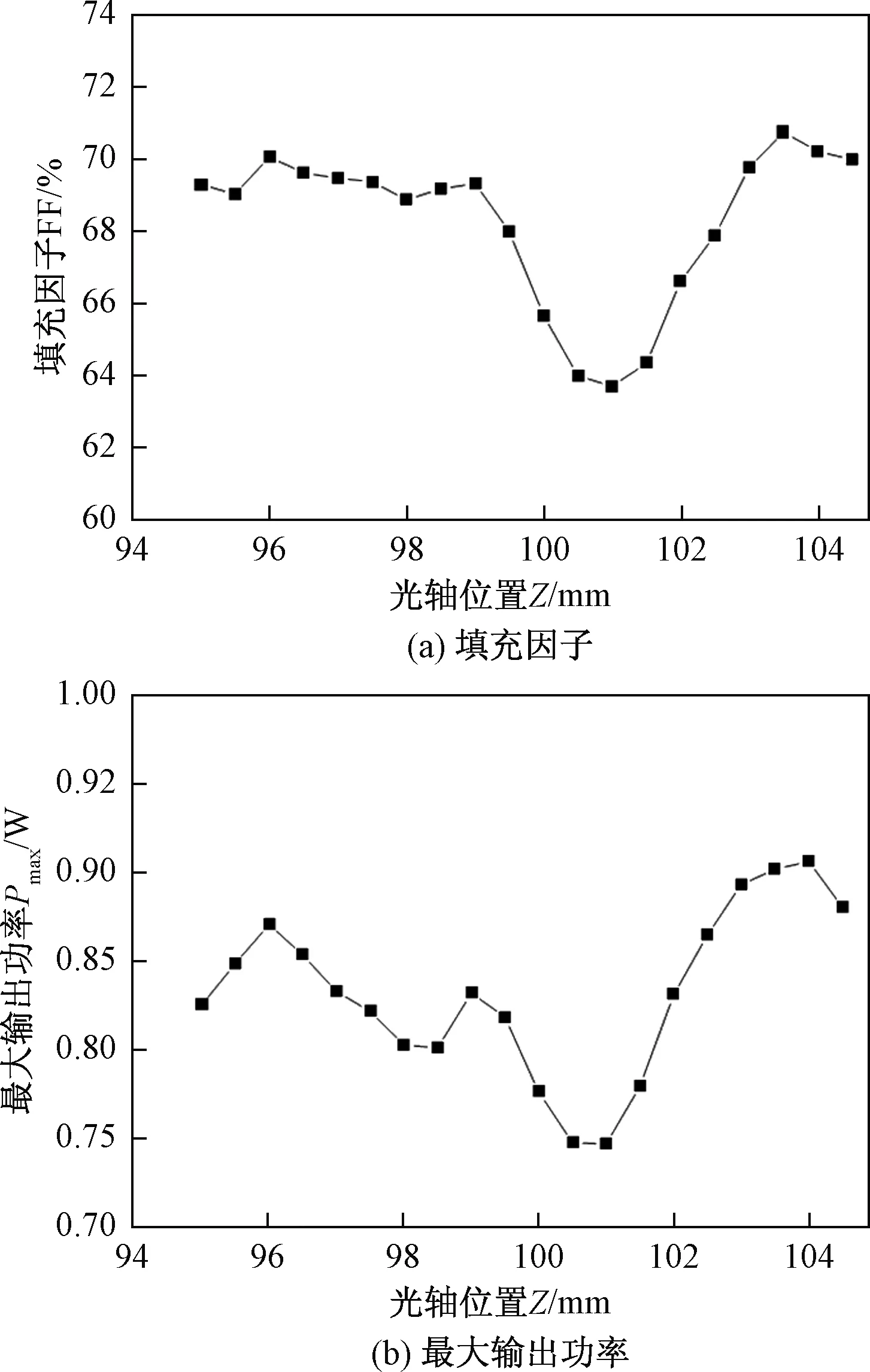
图8 实验数据Fig.8 Experimental data
从实验结果可以看出,实际工作条件下,三结电池放置于菲涅尔透镜焦平面处并非最优。在菲涅尔透镜聚光下,焦平面附近高度的光照非均匀性导致了高倍聚光光伏模组填充因子的下滑,对最大输出功率有负面影响。通过改变三结电池所在的光轴位置,光照非均匀性得到一定程度的改善,当光照非均匀性、电池表面辐射功率、光谱分布等因素的综合影响达到最优时,模组最大输出功率能得到最优值。
5 结论
以GaInP/GaInAs/Ge三结电池的高倍聚光光伏模组为例,通过光线追踪模拟和三维三结电池网络模型,分析沿光轴菲涅尔透镜的光照非均匀性,以及对三结电池输出特性的影响,并结合户外实验进行验证。结果表明沿光轴短、中、长三波段的非均匀性各有不同,峰均比最大值出现在不同的光轴位置,三波段的共同作用使得全波段在102 mm附近光轴区间有较高的峰均比,非均匀性最强。光照的高度非均匀性导致了在该光轴区间横向电流较高,增加了有效串联电阻,宏观上填充因子大幅下降,改变光轴位置能有效提高光照非均匀性,改善填充因子。通过户外实验,发现填充因子在焦平面附近较低,最大输出功率在101 mm处最低。通过优化电池在光轴上的位置,能显著改善填充因子和最大输出功率,在96、104 mm提升12%以上。
通过模拟分析和实验验证,提出通过改变菲涅尔透镜和三结电池的距离,能低成本、简易有效地提升模组工作性能。当辐射功率、光谱分布、光照非均匀性等因素达到平衡时,最大输出功率能获得极大值。模拟和实验结果能为实际模组设计和应用提供有益参考。
