基于二次型跟踪器的实时能量管理优化策略

2020-11-24宋大凤杨丽丽梁伟智李宏程曾小华

科学技术与工程 2020年29期

宋大凤，杨丽丽，梁伟智，李宏程，曾小华

(吉林大学汽车仿真与控制国家重点实验室，长春 130025)

近几年，中国电子商务迅猛发展，快递业务量逐年激增,使得物流车的产销规模展现出扩大的趋势[1]。为了缓解不断增长的物流需求与现代城市健康发展之间的矛盾，混合动力物流车应运而生[2]。混合动力物流车存在多个动力源，在保证整车动力性需求的前提下制定合理的能量管理控制策略协调各动力源的工作状态是发挥其节能优势的关键。

目前，基于规则的能量管理策略是应用最为广泛的可在线实时应用的能量管理策略,然而该策略的制定主要依赖于设计者的经验，其控制效果无法达到最优[3-4]。因此，一些学者应用最优控制理论解决此问题。申彩英等[5]通过减少运算次数对动态规划值算法进行改进以获得各动力源间的最优能量分配；林歆悠等[6]针对混联式混合动力客车应用极小值原理分配发动机和电池之间的功率，实现良好的节油效果。虽然上述两种方法均能求得全局最优解，但具有工况局限性且耗时长的缺陷。胡红斐等[7]以“实时等效能量消耗”最小为目标函数进行优化求解，提出了等效燃油消耗最小策略，但不同工况下的等效因子需要调试以达到最佳控制效果，无法保证经济性最优，故目前对于混合动力系统能量管理策略的研究无法同时兼顾最优性与实时性。

现针对物流车行星式混合动力系统，基于二次型最优控制理论提出一种可在线实时应用的直接节油型二次型跟踪器单自由度策略，基于仿真平台MATLAB/Simulink进行离线仿真验证，获得与全局优化算法相接近的优化结果，并基于dSPACE/Simulator硬件在环测试平台对该策略进行实时性的验证。

1 物流车行星式混合动力系统

1.1 系统构型

以某一款正在研制开发的行星式混合动力系统为研究对象，其构型如图1所示，整车基本参数及主要部件参数如表1所示。

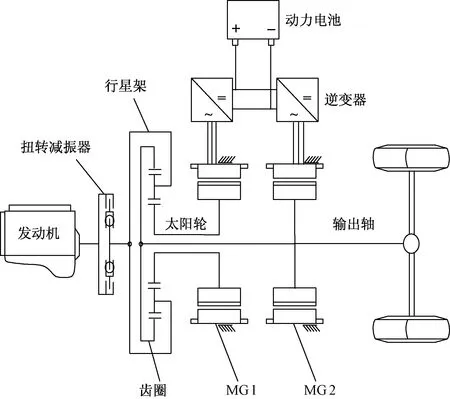
图1 系统构型Fig.1 System configuration

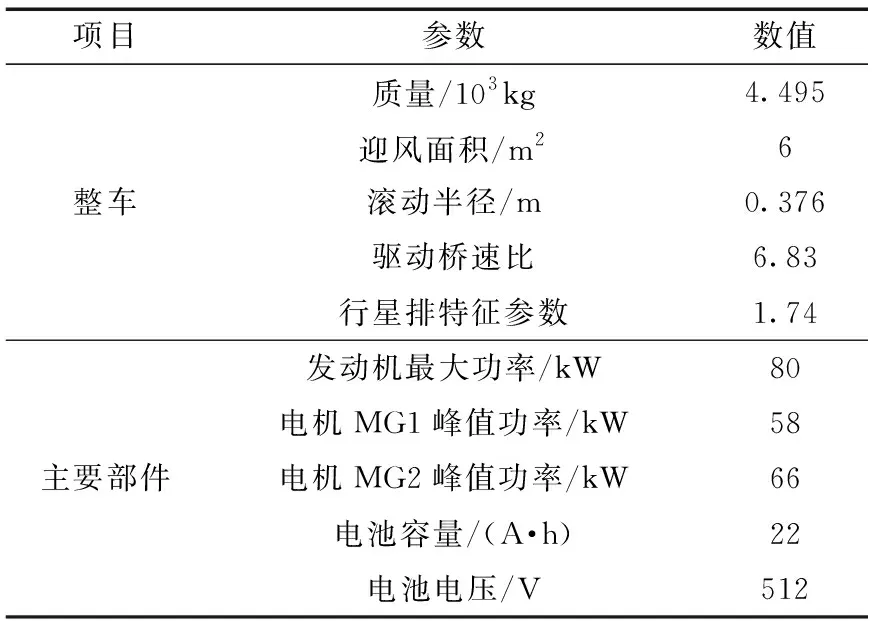
表1 整车及主要部件参数Table 1 Parameters of vehicle and main components

1.2 行星式混合动力系统数学模型

1.2.1 整车动力学模型

由汽车理论可知[8]，汽车行驶方程式为

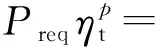
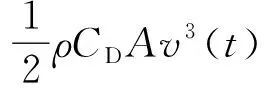
(1)

针对所研究的行星式混合动力系统，整车需求功率由发动机和电池共同提供，即

Preq=Pice+Pbat

(2)

式(2)中：Pice为发动机功率，kW；Pbat为电池组功率，kW。

1.2.2 发动机模型

研究的系统发动机万有特性[9]如图2所示，通过多项式拟合获得发动机功率和燃油消耗率之间的二次函数表达式[10]为

图2 发动机万有特性Fig.2 Universal characteristic of engine

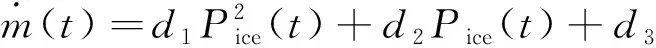
(3)

1.2.3 电池模型

根据电池等效内阻模型，电池组输出功率可以表示为

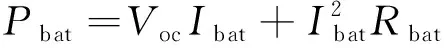
(4)

式(4)中：Voc为电池开路电压，V；Ibat为电池电流，A；Rbat为电池等效电阻，Ω。

由式(4)得到电池电流的表达式为

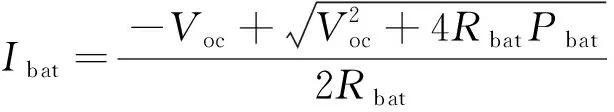
(5)

电池组荷电状态(state of charge, SOC)的改变量可以表示为

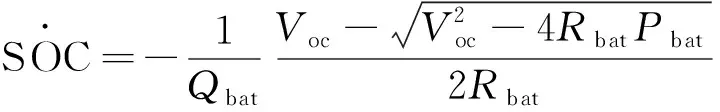
(6)

式(6)中：Qbat为电池组的容量，A·h。

电池组的总能量为

E=QbatVoc

(7)

式(7)中：E为电池组总能量，kW·h。

由式(6)、式(7)可以得到电池组动态特性的表达式为

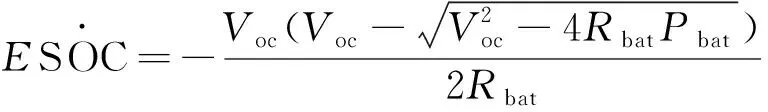
(8)

1.2.4 行星式混合动力系统线性数学模型

(9)

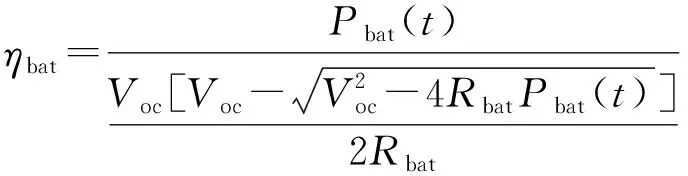
(10)

该线性系统所需满足的约束条件为

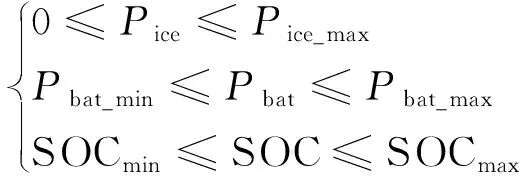
(11)

式(11)中：Pice_max为发动机最大输出功率，kW；Pbat_min和Pbat_max分别对应电池的最大充电功率和最大放电功率，kW；SOCmax为电池SOC的上限，SOCmin为电池SOC的下限。

2 基于二次型跟踪器的能量管理优化策略

依据二次型跟踪器的相关定理[11]，从直接节油的角度开发了一种可实时应用的能量管理优化策略。

2.1 二次型跟踪器单自由度策略开发

根据行星式混合动力系统的线性数学模型，得到线性状态空间方程为

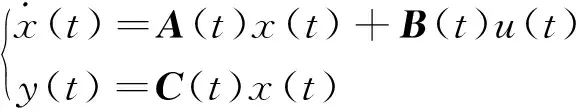
(12)

由式(12)可知，应用线性二次型跟踪器求解行星式混合动力系统能量管理问题，可将其转化为单自由度优化控制问题，即仅与电池SOC相关。

2.2 二次型性能指标设计

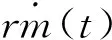
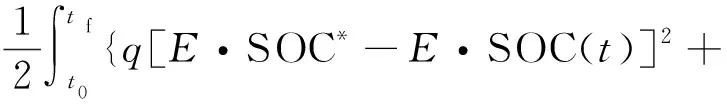
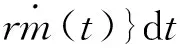
(13)

式(13)中:SOC*为电池期望SOC，q为限制电池能量波动的加权系数；r为限制发动机燃油消耗率波动的加权系数；t0为初始时刻；tf为终端时刻。

将式(3)代入二次型性能指标[式(13)]中，可得：

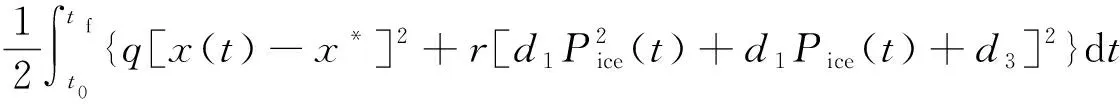
(14)

式(14)中：x*为期望的电池能量值。

将式(2)代入式(14)，可得：

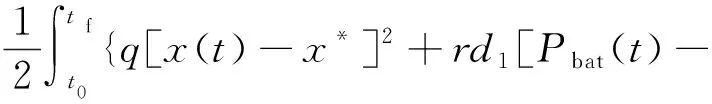
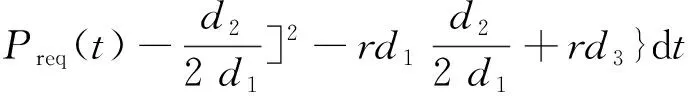
(15)

式(15)中：r、d1、d2、d3均为常数，因此，性能指标中的后两项也均为常数，经简化后的优化性能指标为

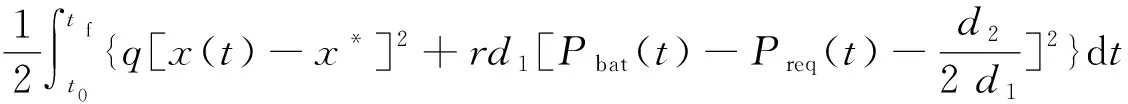
(16)

2.3 最优控制律推导

对于设计二次型性能指标式(16)，指令信号为

z=ESOC*

(17)

因此，系统误差为

e(t)=z-y(t)=E·SOC*-E·SOC(t)

(18)

若令：

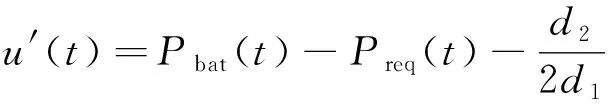
(19)

则得到标准形式的二次型指标性能表达式为

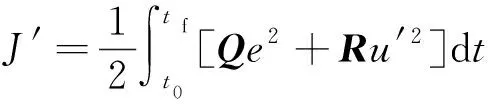
(20)

式(20)中：Q=q；R=rd1。

最优控制律的表达式为

u′*(t)=-R-1BT[Px(t)-g]

(21)

式(21)中：P为黎卡提代数方程的解。

将式(19)代入式(21)，得到最优控制律表达式为

Pbat(t)=-R-1BT{Px(t)+[(A-

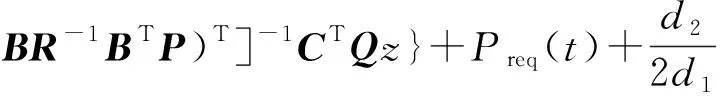
(22)

3 仿真与分析

3.1 离线仿真验证

基于MATLAB/Simulink软件平台建立离线仿真模型，首先对策略中的加权系数进行离线仿真调试，然后对整车的动力性和经济性进行验证。

将式(12)与式(22)相结合，整理得到电池功率为

(23)

式(23)中：黎卡提代数方程的解P通过调用lqr函数进行求解，即[K,P]=lqr(A,B,Q,R)。

由此可知，特定工况下的电池功率仅由状态变量和加权系数决定。系统状态方程中A=0，故该系统所对应的黎卡提矩阵代数方程为

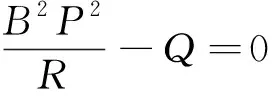
(24)

由式(23)得到最优反馈增益K为

(25)

由式(25)可知，当Q与R的比值确定时，则可以确定最优反馈增益K。经过试凑，得到该策略中的加权系数、黎卡提代数方程的解及反馈增益，如表2所示。

表2 加权系数、黎卡提代数方程的解及反馈增益Table 2 Weighting coefficient, solution of Riccati algebraic equation and feedback gain

在C-WTVC工况下的离线仿真结果如图3所示，可以看出，实际车速能够良好地跟随目标车速，表明该策略能够满足整车动力性需求，电池SOC初始值和终值均为70%，表明能够良好地跟踪期望电池SOC，可维持电量平衡。

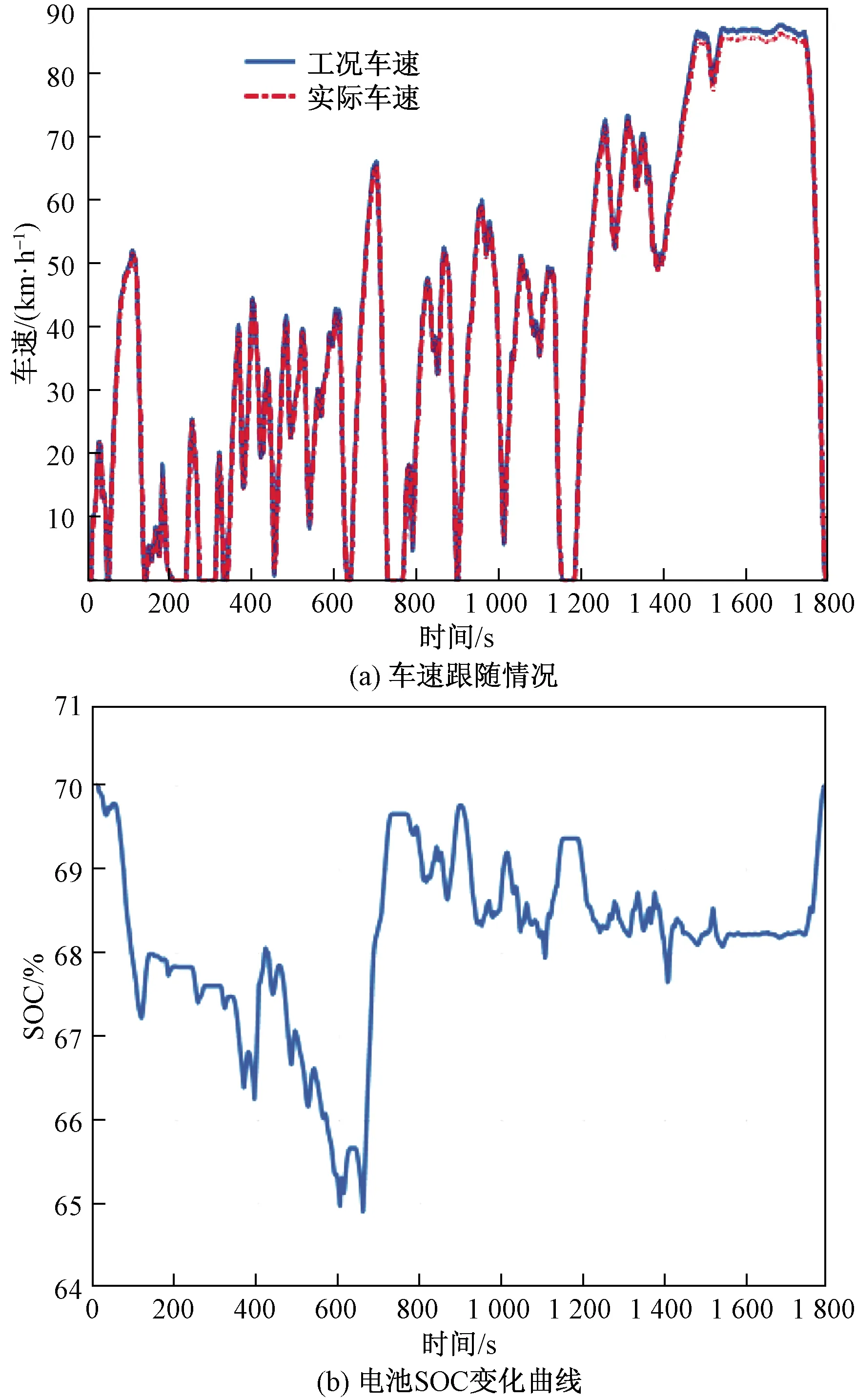
图3 离线仿真结果Fig.3 Offline simulation results

为验证在不同电池SOC初始值下提出的策略能够良好地跟踪指令信号，分别在电池SOC初始值取60%、65%、70%、75%、80%时进行了离线仿真，如图4所示。设定电池SOC期望值为70%，可以看出在不同的电池SOC初始值下都能良好地跟踪期望电池SOC，电池SOC终值均为70%，均能维持电量平衡。

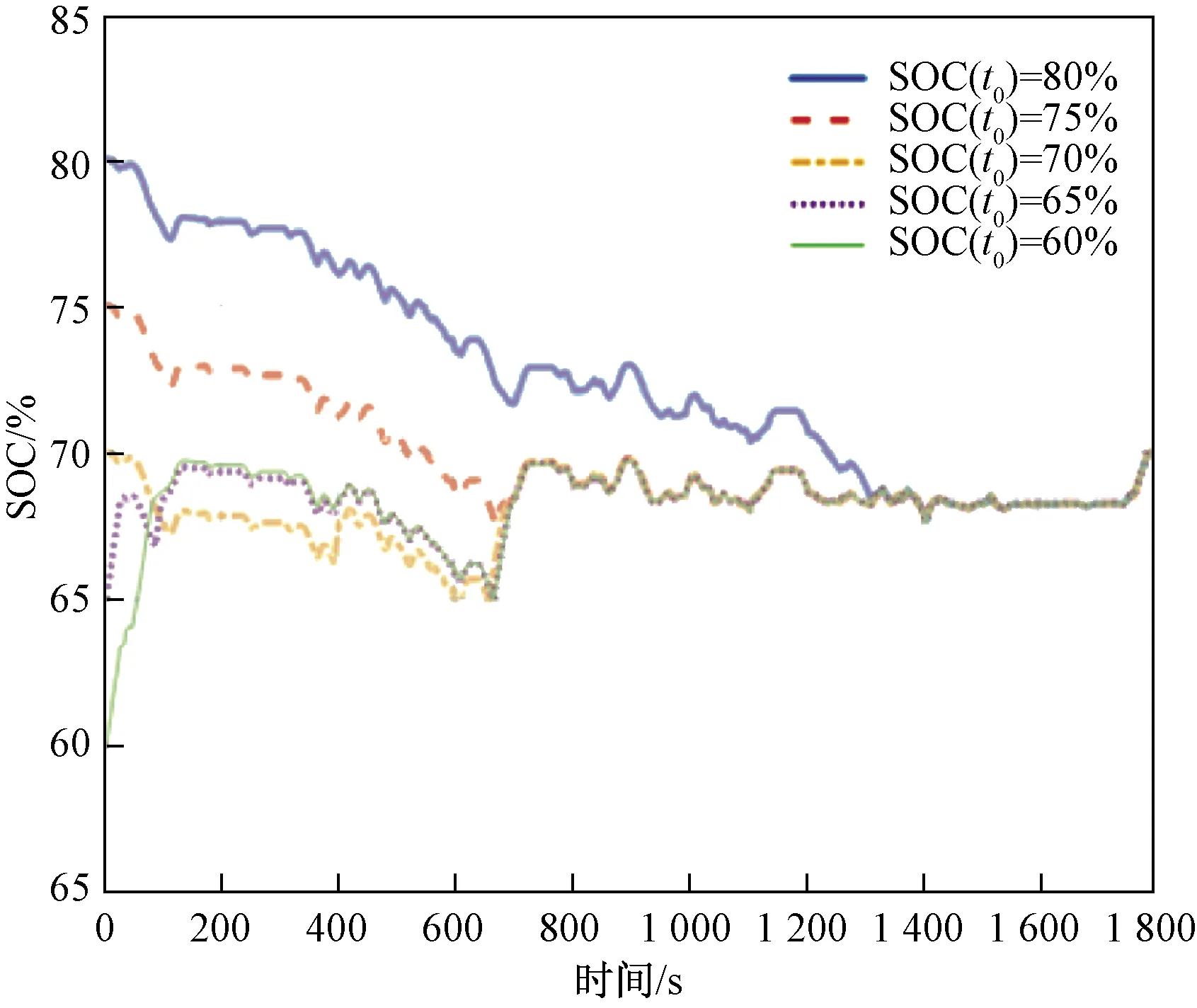
图4 不同初始值下电池SOC变化曲线Fig.4 Battery SOC curve under different initial values

3.2 仿真结果对比分析

基于动态规划算法的全局控制策略求得特定工况下的最优解[12]，并以其仿真结果为基础来评估所提出的策略[13-14]，两种策略仿真结果的对比如表3所示，均能实现电量平衡，本文的策略能获得与全局优化算法相近的节油效果，且提高了运算速度，应用简单、方便。

表3 不同策略离线仿真结果对比Table 3 Comparison of offline simulation results of different strategies

3.3 硬件在环测试

搭建了硬件在环(hardware-in-the-loop，HIL)测试平台[15]，如图5所示，并进行了硬件在环测试。该测试平台主要包括实时仿真控制器dSPACE/Simulator、实际控制器和上位机。

图5 HIL测试平台Fig.5 HIL test platform

为使测试效果达到接近实车控制的效果，首先基于实车控制策略架构搭建控制策略模型，然后将控制策略下载到实际控制器中进行测试，并且功能模块中的系统约束模块考虑了实际情况下系统中电池、发动机、电机MG1、MG2的功率限制、温度和故障状态对其工作特性的影响。

在C-WTVC工况下进行测试，得到的硬件在环测试结果如图6所示，可以看出，在实时环境下提出的控制策略能够良好地跟随车速，二次型跟踪器单自由度策略离线仿真与HIL测试结果对比如表4所示，电池SOC初始值为70%，终值为69.96%，能够实现电量平衡，并且该控制策略在不同的电池SOC初始值下均能良好的跟踪期望电池SOC。仿真结果证明了二次型跟踪器单自由度策略能在实时环境下应用并具有良好的控制效果，为动态规划全局优化算法的次优解。