复合固体推进剂颗粒与基体初始界面有无缺陷的细观模型对比

侯宇菲，许进升，周长省，陈雄，李宏文

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.晋西工业集团有限责任公司，山西 太原 030027)

0 引言

端羟基聚丁二烯(HTPB)推进剂作为一种多相(基体相、增强相、界面相)含能材料，广泛应用于各类火箭武器。HTPB的宏观力学性能取决于颗粒、基体及颗粒与基体界面的力学性质，因此从细观角度上视为一种非均质材料[1]。van Ramshorst等[2]和王阳等[3]基于扫描电镜(SEM)对HTPB推进剂细观形态与宏观变形及失效之间的关系进行了研究，发现在外载荷作用下，颗粒与基体界面发生脱粘，且裂纹沿着颗粒与基体界面生长，从而引起推进剂力学性能非线性。因此，有必要对复合固体推进剂颗粒与基体界面脱粘进行分析。

Matouš等[4]、常武军等[5]、Inglis[6]在小应变条件下，采用随机夹杂颗粒填充模型对推进剂颗粒与基体界面脱粘过程进行了数值模拟。刘承武等[7]考虑推进剂基体材料大变形的特点，建立了Mori-Tanaka有限元方法，然而随着界面脱粘程度的加深，基于Mori-Tanaka有限元法计算的应力值偏高，从而无法准确描述推进剂加速损伤的特点。韩龙[8]和Dai等[9]通过修正内聚力法则，得到不同应变率下颗粒与基体界面非线性脱粘的损伤演化规律，然而模型的预测应力值均大于实验应力值。究其原因，是因为以上研究假设固体推进剂颗粒与基体界面为有效粘结，并未考虑初始界面缺陷对推进剂力学性能的影响，因此导致预测应力值偏高。Balzer等[10]通过SEM对推进剂颗粒与基体界面在拉伸初始时刻进行观察，发现部分颗粒与基体之间存在微小孔洞。这是因为推进剂在固化降温过程中颗粒与基体的材料属性不同，导致其形变存在差异，造成颗粒与基体之间形成间隙，使得推进剂内部存在随机分布的初始界面缺陷。刘晋湘等[11]通过颗粒与基体界面含初始缺陷试样以及颗粒与基体界面无初始缺陷试样的单轴拉伸实验发现，初始界面缺陷决定材料的失效路径，并且高氯酸铵(AP)颗粒与基体初始界面损伤会降低初始界面的粘结强度，导致推进剂更容易发生损伤。黄海峰等[12]和文志杰等[13]在研究岩石断裂时发现初始缺陷对细观非均匀材料宏观力学性能的影响不容忽略，并利用Weibull函数对岩石材料的本构模型进行修正，能够更准确地描述这类材料的非线性力学特征。

本文采用通用有限元分析软件Abaqus的Abaqus/Explicit求解器，结合VUMAT获得指数内聚力法则，利用Weibull分布作为颗粒与基体界面粘结强度的密度函数，建立考虑初始缺陷的细观颗粒填充模型，通过对比数值仿真与实验结果验证所建立模型的准确性。

1 细观颗粒填充模型

1.1 颗粒填充模型

以HTPB复合固体推进剂为例，采用分子动力学算法[8]生成与实际推进剂具有相同体积分数的细观颗粒填充模型，填充比例如表1所示。其中，填充铝(Al)粉与AP颗粒粒径分布服从图1所示的双峰分布规律。根据文献[14]得知，当代表性体积单元尺寸为最大颗粒粒径的3～5倍时，认为其有效。因此，本文选用的代表性体积单元尺寸为500 μm×500 μm，如图2所示。

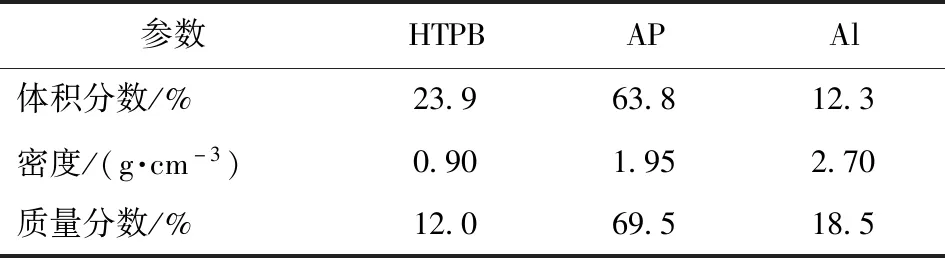
表1 HTPB推进剂基本组分Tab.1 Components of HTPB propellant

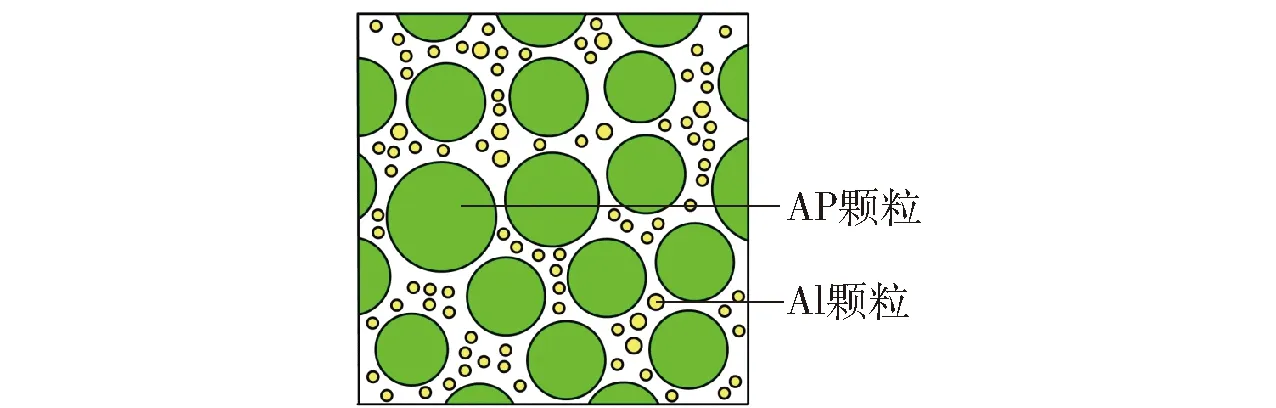
图2 细观颗粒填充模型Fig.2 Microscopic particle packing model

图2中，AP颗粒与Al颗粒的最大粒径之比约为20∶1，若直接对该模型进行网格划分，则将导致网格质量降低，进而仿真计算结果无法收敛。文献[15]通过实验证明，由于Al颗粒与基体材料的界面浸润能力较强，固体推进剂在搅拌固化过程中，颗粒与基体界面无脱粘现象。因此，通过Mori-Tanaka[16]解析法将Al颗粒等效到基体材料中，在数值模拟过程中只考虑AP颗粒对材料力学性能的影响，并将此类基体称为等效基体，材料参数如表2所示。

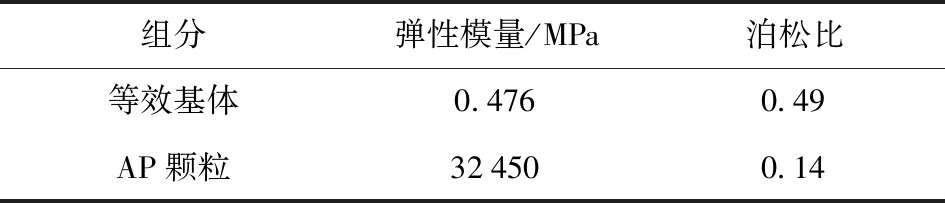
表2 HTPB推进剂的材料参数Tab.2 Material parameters of HTPB propellant

1.2 粘结单元

为模拟颗粒与基体间的界面，本文采用Python脚本语言开发零厚度粘结单元，如图3所示。为方便理解，图3给出了粘结单元的几何厚度，实际计算过程中几何厚度为0 mm.

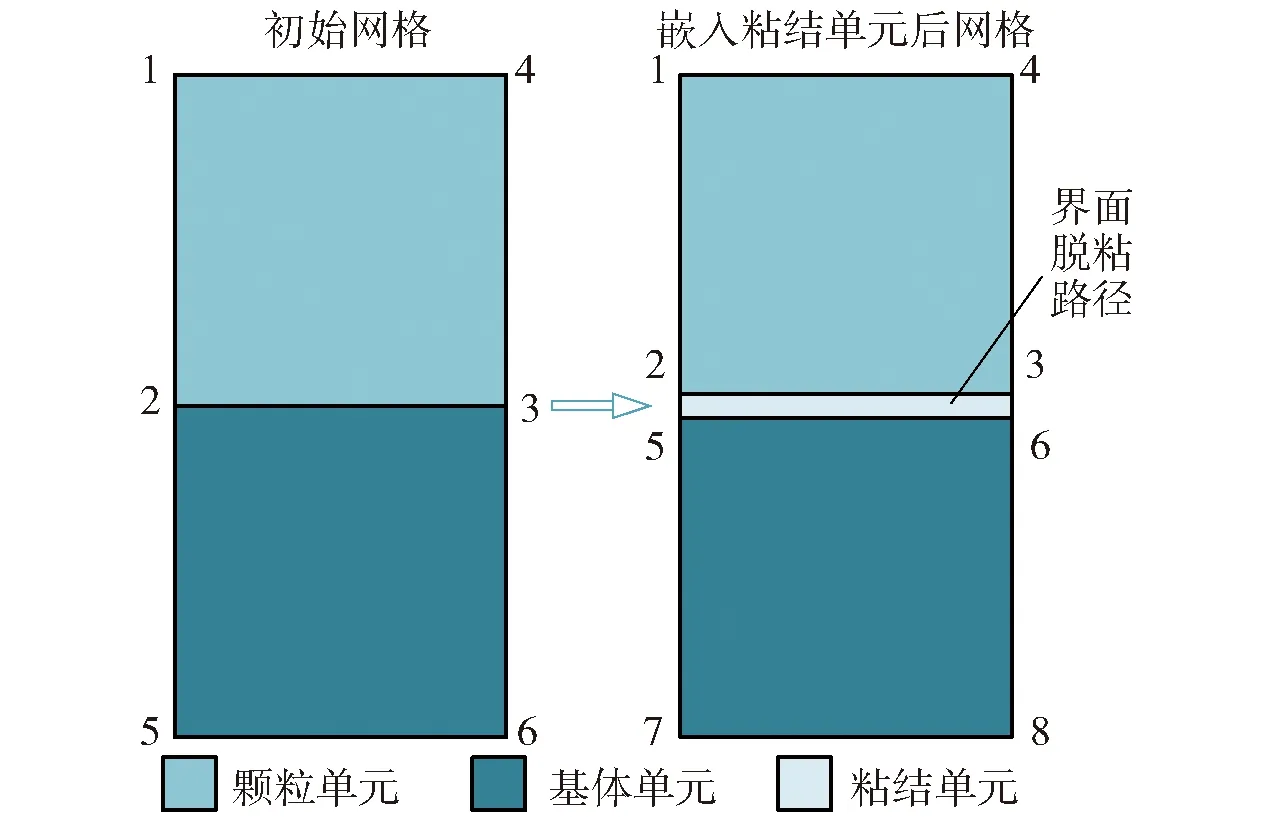
图3 粘结单元嵌入示意图Fig.3 Schematic diagram of cohesive element embedding

1.3 指数内聚力法则

内聚力法则最早由Dugdale[17]和Barenblatt[18]提出，他们认为在裂纹尖端处存在一个断裂过程区，此区域呈现了裂纹尖端及附近的损伤机制，并引入了内聚力和间距的本构关系，以及内聚力法则，通过该法则可以模拟断裂区域内能量的耗散过程。内聚力模型根据其曲线形式可分为双线性、多项式、指数型等，每种形式的应力- 位移关系都有其适用范围。根据推进剂在载荷作用下的加速损伤特性，本文采用指数型内聚力法则描述颗粒与基体界面的损伤演化过程。

由于在计算过程中使用了0 mm厚度粘结单元，指数内聚力法则需通过VUMAT子程序二次开发得到[19]。指数内聚力法则的断裂能φ(t)为

(1)

式中：φn为纯法向开裂状态下的界面断裂能；tn和tt为界面的法向与切向位移；δn和δt为法向与切向界面开裂时的特征位移；参数q和r分别由(2)式和(3)式确定：

(2)

(3)

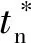
(4)

(5)

式中：Tn与Tt分别为法向应力值与切向应力值。

通过(4)式和(5)式发现，指数内聚力法则中的Tn和Tt由法向位移和切向位移同时决定，因此更符合实际界面开裂的应力状态。

1.4 Weibull分布

复合固体推进剂在制备过程中受工艺和材料特性的限制，内部存在大量随机分布的初始缺陷。其中包括少量气孔和搅拌过程中由于颗粒碰撞引起的颗粒破碎，更多的缺陷是在固化降温时，颗粒与基体界面浸润能力下降导致的颗粒与基体界面间产生空隙，如图4所示。这些初始缺陷的存在导致HTPB复合固体推进剂在进行单轴拉伸重复性实验时，应力- 应变曲线的分散性增加，进一步导致材料整体强度降低，因此在预测推进剂的力学性能时需要考虑颗粒与基体界面间的初始缺陷。通常使用Abaqus软件对颗粒与基体界面材料属性进行定义时，会默认所有颗粒与基体界面属性均相同。目前有两种方法可以表达材料细观界面的非均质性：1)将颗粒与基体界面划分为不同集合；2)采用自开发程序，将材料属性设置为积分点的函数。方法1由于计算效率低而无法适用于高颗粒填充比材料。方法2可以随机定义材料属性，能够准确模拟界面开裂时的真实状态，因此本文采用方法2实现颗粒与基体界面的非均质性。文献[20]认为航空、航天工业中的复合材料特性符合Weibull分布。因此本文将颗粒与基体界面粘结强度的密度函数设置为Weibull函数，建立考虑初始缺陷的HTPB复合固体推进剂细观数值模型。Weibull函数概率密度f(x)表达式为

图4 固体推进剂初始缺陷示意图Fig.4 Initial defect of solid propellant

(6)

式中：x表示随机函数；m为形状参数；λ为比例参数。形状参数m反映了f(x)的离散程度，m越大，分散性越小，材料的可靠度越高，如图5所示。

图5 Weibull分布密度函数Fig.5 Weibull distribution density function

1.5 内聚力参数及边界条件

为模拟HTPB推进剂在单轴等速拉伸下颗粒与基体界面脱粘的过程，对所建立的细观模型选用合理边界条件进行数值模拟，如图6所示。图6(a)、图6(b)、图6(d)的下边界施加固定约束载荷、上边界作为载荷承载端，其中：图6(a)左边界和右边界为无约束边界；图6(b)左边界和右边界为竖直边界，即在变形过程中边界保持竖直；图6(d)左边界和右边界为周期性边界；图6(c)上、下、左、右边界均为周期性边界。文献[21]认为若代表性体积单元尺寸选取适当，则图6(a)、图6(b)、图6(c)的边界条件对数值计算结果影响较小。图6(d)中，由于轴约束不匹配，导致计算结果与实际情况不符。本文所考虑的颗粒分布状态呈非周期性，故选用图6(b)中的边界条件进行数值计算。

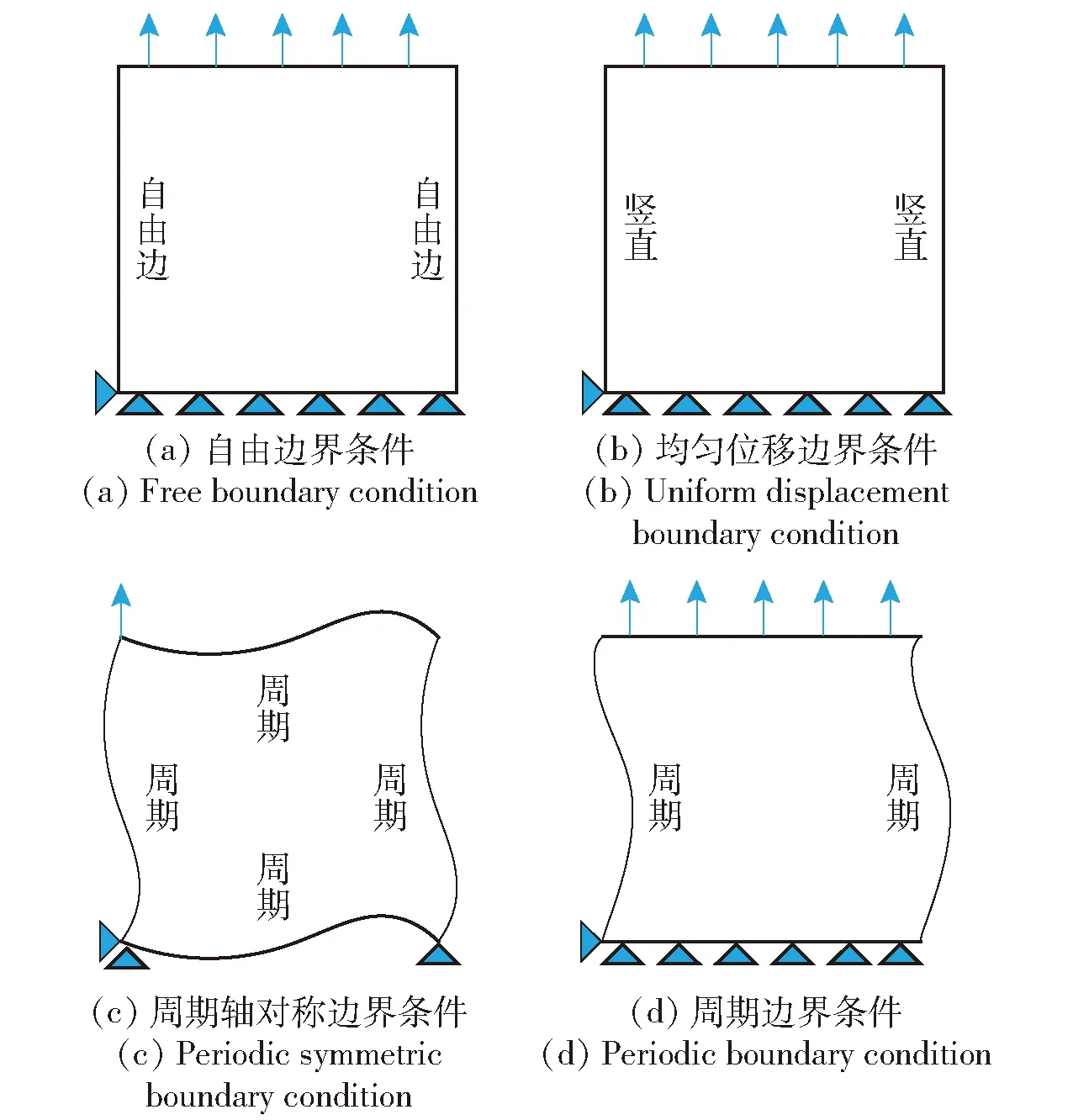
图6 边界条件Fig.6 Boundary conditions

由于目前实验手段的局限性，很难获得微米级颗粒与基体界面间的粘结能，普遍采用的方法是通过实验反演法获得内聚力模型的材料参数。主要包括如下3个步骤：1)采用材料实验机对HTPB复合固体推进剂试样进行单轴拉伸实验，实验环境温度为20 ℃，湿度保持在40%±5%范围内，实验机加载速率为1 mm/min，实验重复3次，从而获得HTPB复合固体推进剂的单轴拉伸应力- 应变曲线，如图7所示；2)建立考虑初始缺陷的固体推进剂细观模型，假设试样3无颗粒与基体初始界面缺陷，并将其应力- 应变曲线定为目标函数；3)根据文献[22-23]中的Hook-Jeeves优化算法使仿真应力- 应变曲线尽可能接近目标函数，当仿真曲线与目标函数误差值小于设定阈值时，确定内聚力模型材料参数，具体反演过程见文献[22]。

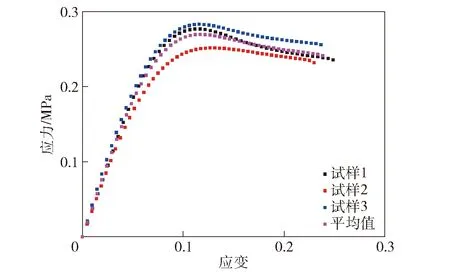
图7 实验应力- 应变曲线Fig.7 Experimental stress-strain curves of propellant

指数内聚力模型只需确定粘结强度σmax和特征位移δc即可，反演后的参数如表3所示。

表3 指数内聚力参数Tab.3 Exponential cohesive parameters

2 结果分析

2.1 无缺陷模型仿真结果

为消除有限元模型网格尺寸所带来的计算误差，对模型的网格收敛性进行计算，取网格尺寸y分别为0.040 mm、0.020 mm、0.010 mm、0.005 mm，如图8所示。4种网格尺寸的计算模型，其颗粒与基体界面采用指数内聚力法则，各点粘结强度均相同，不考虑初始缺陷，称这种模型为无缺陷模型。由于计算结果较多，下面仅给出网格尺寸为0.01 mm的模型应力计算云图，如图9所示。

图8 网格尺寸Fig.8 Mesh size

从图9中可以看出，颗粒与基体材料的应力变化分为3个阶段。当应变ε为0.03时，模型整体未出现损伤，此时推进剂处于弹性阶段。当应变ε为0.05时，颗粒作为弹性体，其弹性模量远大于基体材料弹性模量，当应变相同时，颗粒承受的应力大于基体承受的应力，导致颗粒与基体界面成为推进剂结构中的最薄弱区域，在载荷的持续作用下，颗粒与基体界面发生位移分离。对于单一粒径配方，模型中部的颗粒与基体界面最先发生损伤。当应变ε为0.10时，颗粒与基体界面发生脱粘，部分颗粒从微孔洞中裸露出来，此时颗粒两极不再受力，其赤道处出现高应力区。最终，高应力区形成微裂纹，进而导致推进剂失效破坏。

下面通过弹性模量- 应变曲线分析推进剂细观失效时的力学响应，如图10所示。由图10可见：拉伸初始阶段，初始弹性模量恒定，模型处于弹性阶段；当应变继续增大时，弹性模量开始下降，结合应力云图可以发现颗粒与基体界面发生脱粘，由此得知颗粒与基体界面脱粘会导致推进剂弹性模量下降。

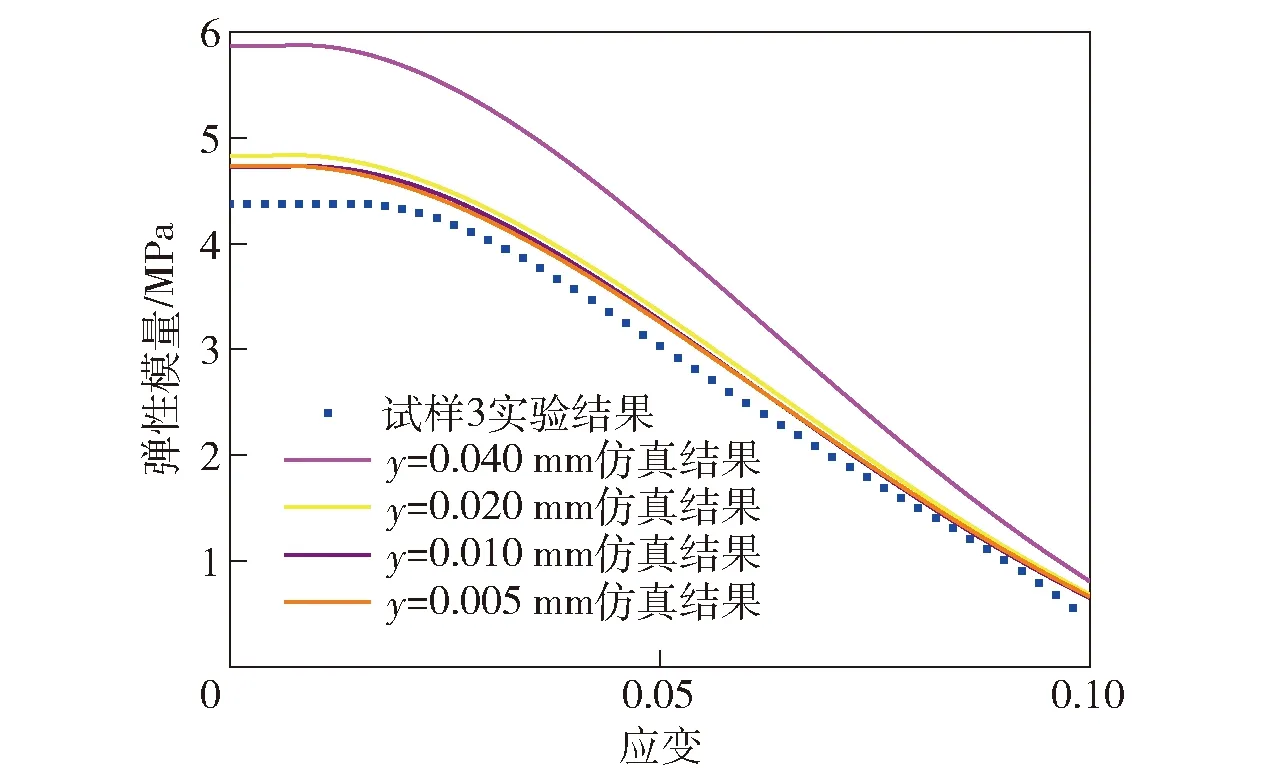
图10 无损伤模型弹性模量- 应变曲线Fig.10 Modulus-strain curves of damage-free model

对比图10中不同网格尺寸的无缺陷模型预测结果与试样3的实验结果发现，无缺陷模型对网格尺寸的敏感性较高，模型预测结果随着网格尺寸的减小而接近实验结果。当网格尺寸为0.020 mm时，模型对网格尺寸的敏感性大幅度降低，计算结果收敛。为考察网格尺寸对细观模型应力场的影响，下面给出模型整体应变为0.06时，模型网格尺寸为0.005 mm与0.040 mm的应力云图，如图11所示。由图11可见：粗网格模型的应力过渡区有大量锯齿状区域出现，且连续性较差，过度不均匀；细网格模型的应力过度区光滑，其应力场分布连续性较好。以上分析表明，为提高无缺陷模型计算结果的准确性，需采用合适的网格尺寸。

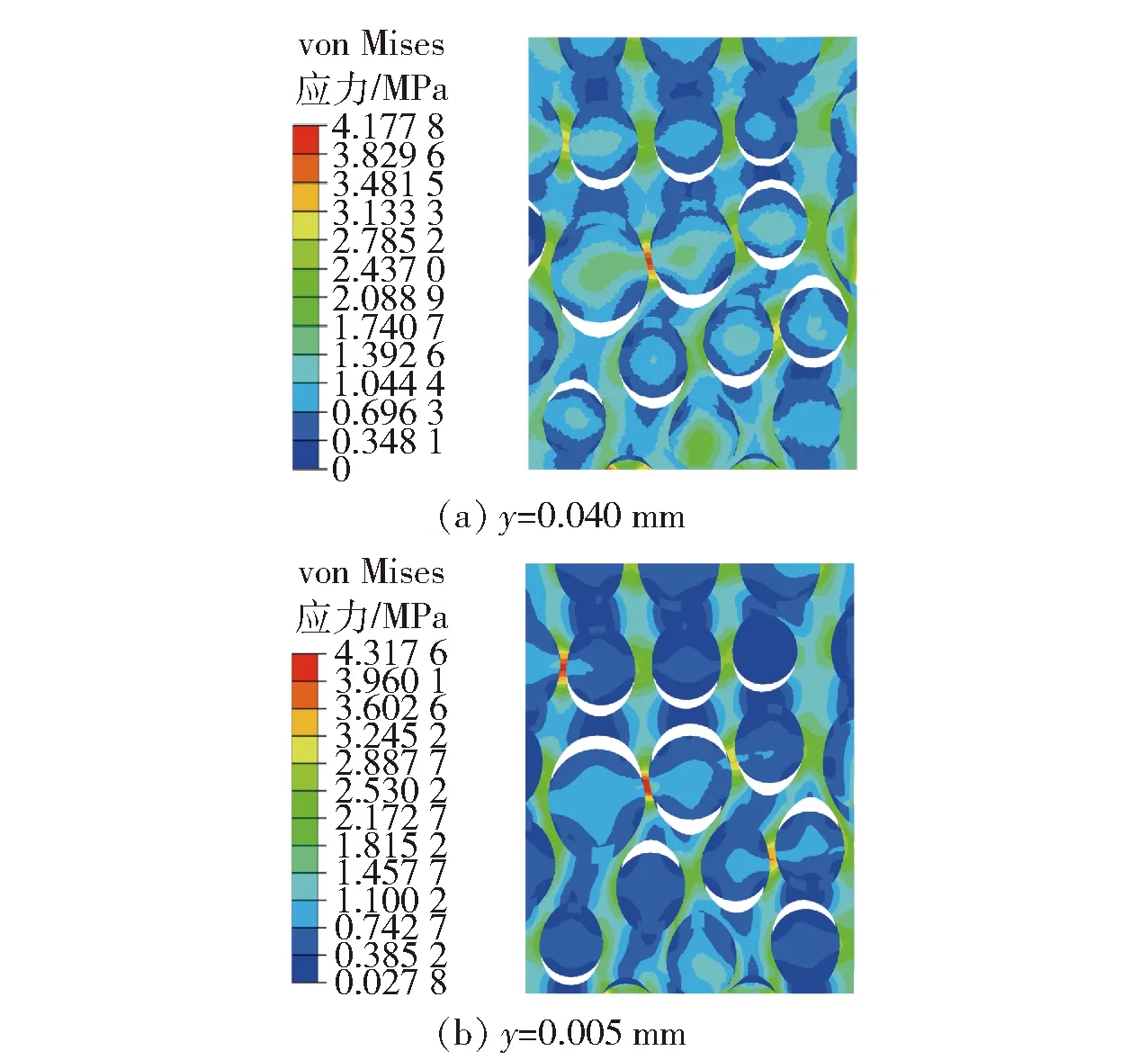
图11 不同网格尺寸的von Mises应力云图Fig.11 von Mises stress nephograms with different mesh sizes

2.2 初始缺陷损伤模型结果分析

采用2.1节的4种网格尺寸，对初始缺陷模型进行数值仿真，其颗粒与基体界面粘结强度的密度函数呈Weibull分布。从图5得知，粘结强度分布密度与形状参数m有关，为确定符合复合固体推进剂材料粘结强度的分布规律，将m分别取值为2.0、2.5、3.0、3.5、4.0、4.5、5.0代入计算模型中进行数值模拟。由于模型数量较多，下面只给出m=3.0时网格尺寸为0.010 mm的初始缺陷模型应力云图，如图12所示。

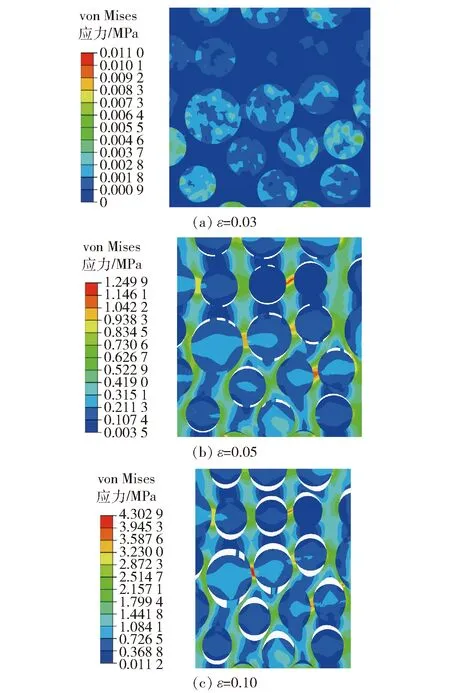
图12 初始缺陷损伤模型的von Mises应力云图Fig.12 von Mises stress nephograms of initial damage model

由图12可见，初始缺陷模型与无缺陷模型的应力云图变化过程类似，其应力云图变化同样分为3个阶段，但二者的第2阶段存在明显区别。在无缺陷模型中，位于模型中部的颗粒最先发生脱粘，并且由于颗粒与基体界面的粘结强度相同，颗粒两级处应力最大，颗粒与基体界面脱粘从极点沿两侧缓慢进行。而在初始缺陷模型中，由于界面粘结强度分布的非均匀性，颗粒与基体界面脱粘位置发生改变，不再是位于模型中部的颗粒率先发生界面脱粘，而是颗粒与基体界面损伤含量较高的位置率先发生脱粘；并且位于极点周围的区域均为初始脱粘区，如图12(b)所示。初始缺陷模型更好地解释了推进剂在进行重复拉伸实验时试件断裂位置的不可预估性。

为了更直观地分析初始缺陷对复合固体推进剂力学性能的影响，本文给出了初始缺陷模型的弹性模量- 应变曲线，如图13所示。

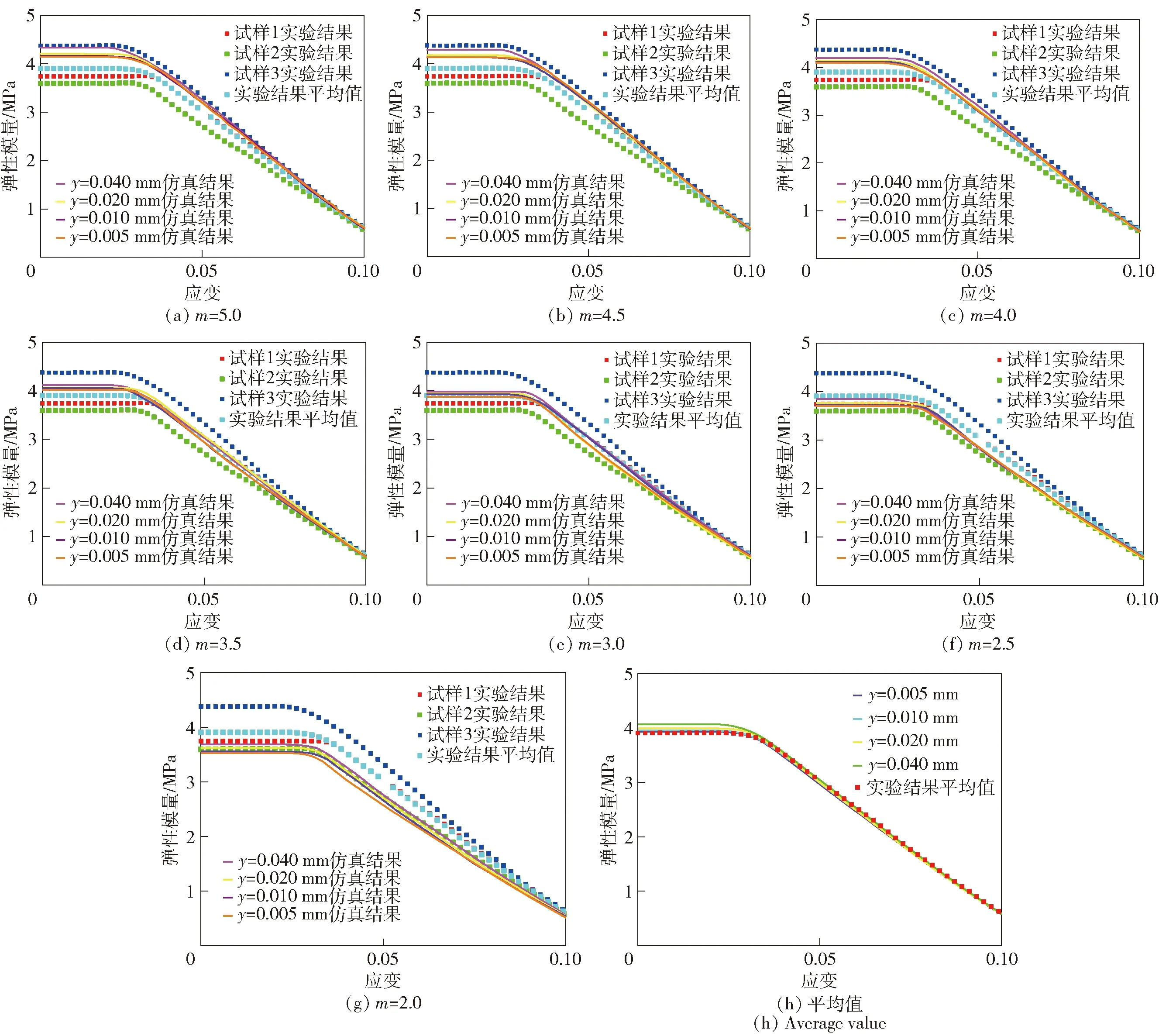
图13 初始缺陷损伤模型的弹性模量- 应变曲线Fig.13 Modulus-strain curves of initial damage model

从图13(a)～图13(g)中可以看出，初始弹性模量随形状参数m值降低而减小。这是因为m值决定了颗粒与基体界面粘结强度的分布规律，m值越小，粘结强度分布越分散，细观模型内部的初始缺陷越多，颗粒与基体界面发生脱粘损伤的概率越大，从而界面传递载荷能力下降，导致模型的整体强度下降。在相同应变条件下对应的应力越低，最终导致初始弹性模量下降。相反，m值越大，粘结强度分布越集中，数值计算结果得到的初始弹性模量越高。为了进一步证明初始缺陷损伤模型是否符合真实推进剂的力学状态，将所有模型的计算结果求均值并与实验结果比较，如图13(h)所示。从图13(h)中可以看出，仿真结果与实验结果基本吻合，表明本文所建模型有效，同时也表明推进剂在制备过程中，推进剂内部存在随机分布的初始缺陷，因此需要采用考虑初始缺陷的细观模型对其进行力学性能分析。

对比图10与图13(h)发现，初始缺陷损伤模型对网格尺寸的敏感性大幅度降低，计算所得初始弹性模量最大值与最小值的相对误差小于4%，提高了网格收敛性。众所周知，网格数量越多，模型的计算时间越长，导致计算成本增加。因此，可以采用初始缺陷损伤模型代替无缺陷损伤模型进行数值计算，从而降低计算成本。

3 结论

本文基于Abaqus有限元软件建立了HTPB复合固体推进剂颗粒填充模型，分析了颗粒与基体初始界面缺陷对推进剂力学性能的影响。得出如下主要结论：

1) 针对HTPB复合固体推进剂颗粒与基体初始界面缺陷问题，本文以Weibull分布作为颗粒与基体界面粘结强度的密度函数，分别建立了无缺陷模型与初始缺陷模型。数值仿真结果表明：初始弹性模量随着颗粒与基体初始界面缺陷含量的增多而降低。

2) HTPB复合固体推进剂细观损伤分为3个阶段：弹性阶段、颗粒与基体之间产生位移分离、颗粒与基体界面脱粘并形成孔洞。结合仿真结果与应力应变曲线得知：颗粒与基体界面脱粘引起推进剂弹性模量降低，改善颗粒与基体之间的浸润能力是提高复合固体推进剂力学性能的关键。

3) 网格尺寸敏感性分析表明：无缺陷模型与初始缺陷模型的数值计算结果随着网格尺寸减小而收敛，并且初始缺陷模型的网格尺寸敏感性较低，在后续工作中可采用初始缺陷模型来降低计算成本。