高速旋转弹丸炸药装药在膛内运动中底层温度的数值模拟

2020-11-24彭嘉诚蒋建伟廖伟

兵工学报 2020年9期

彭嘉诚，蒋建伟，廖伟

(北京理工大学爆炸科学与技术国家重点实验室，北京 100081)

0 引言

由身管武器发射的弹丸由于膛内异常引发的膛炸、早炸事故，不仅不能完成预定任务，而且往往造成重大人员伤亡和装备损失等严重后果，故弹丸发射安全性问题一直受到研究人员广泛关注。

早期，研究人员对膛炸现象的研究主要集中在直接引发事故的火工品，如发射装药和引信[1-6]。由高膛压线膛火炮发射的高速旋转弹丸在膛内过载大，受火药力驱动，不仅作轴向运动，还因弹带受膛线切割而绕弹轴作高速旋转运动。因此，高速旋转弹丸发射安全性问题具有一定特殊性。目前，针对高速旋转弹丸膛内运动状态尚无有效理论和试验方法进行准确计算或观测。近年来，有学者采用数值模拟方法对线膛炮发射高速旋转弹丸膛内运动过程开展了研究。文献[7-10]采用数值模拟方法完成了不同弹炮间隙、卡膛速度、初始摆角及摩擦热等因素对膛内弹丸挤进过程的影响规律研究，证明了数值模拟方法应用在弹丸膛内运动过程研究的有效性。许耀峰等[11]针对某大口径火炮膛线结构对滑动弹带弹丸膛内运动的影响进行了数值分析；徐赫阳等[12]采用LS-DYNA软件，对某线膛火炮战斗部发射强度开展了数值模拟研究；王韫泽等[13]针对膛内存在异物时弹体和身管的动态响应进行数值仿真，探讨了穿甲弹近炮口膛炸机理。然而，针对由膛内弹丸高速旋转引发的发射安全性问题的研究还较少。

高速旋转弹丸的炸药装药通常采用压装、铸装、直接装填压装药柱等方式。其中，装填压装药柱方式工艺简单、效率高，已得到较广泛应用。该装药方式的工艺要求在装药表面或弹体内壁浸涂一层粘结剂以增大装药与弹体间摩擦，防止在弹丸运输、使用过程中炸药装药在弹体内窜动。然而，发射时外界环境若处于极端条件下如异常高温等，浸涂的粘结剂易软化、融化，极可能失去增大装药与弹体间摩擦的功能。特别地，高速旋转弹膛内弹带受膛线切割带动弹体绕轴旋转，而弹体只能依靠摩擦力带动装药旋转。若弹体与炸药装药间摩擦系数过小，则二者可能发生相对旋转，导致高速旋转弹丸膛内过程出现异常。

本文针对由高膛压线膛火炮发射的高速旋转弹丸发射安全性问题开展研究，基于摩擦产热- 热传导- 升温理论，建立高速旋转弹膛内炸药装药温度计算模型。结合某大口径高速旋转弹丸出炮口一段距离后装药早炸、掉弹事故，采用LS-DYNA软件数值模拟该弹膛内运动全过程，获取炸药装药底面压力和装药与弹体相对角速度随时间变化规律，并结合MATLAB软件获取其具体函数形式。最终计算得到膛内过程装药温度变化，结合热爆炸理论分析引发事故的主要原因。本文建立的装药温度计算模型及计算方法可为该类弹丸炸药装药结构设计和工艺改进提供理论指导。

1 模型建立

1.1 问题分析

由线膛炮发射的高速旋转弹丸由于异常条件导致炸药装药与弹体间摩擦系数过小，膛内弹体无法带动药柱作同步旋转，炸药装药不同部位将与弹体发生强摩擦。其中，装药底面与弹体完全接触且持续受弹体较大的轴向作用力，此处强摩擦将产生大量热量，热传导至装药后在弹体内部密闭空间内不能快速散失，沉积在装药表面，造成底层炸药快速升温，极易引发膛炸、早炸事故。图1所示为表述该现象的装药与弹体简化模型(剖面)。图1中，p为弹体轴向压强(Pa)。

图1 装药与弹体简化模型Fig.1 Simplified model of charge and projectile body

为对上述现象进行定量分析，将弹膛内运动全过程分为装药与弹体间强摩擦力做功、产热过程和热传导炸药装药及底层炸药升温过程，结合相关理论建立底层炸药温度计算模型。

1.2 摩擦力做功产热

膛内装药与弹体相对转动时，在接触面上将发生强摩擦。假设摩擦力做功完全转化为热量，

Q=W=μF·L，

(1)

式中：Q、W分别为摩擦力做功产热量与做功量(J)；μ为动摩擦因子；F为炸药装药表面所受正压力(N)；L为摩擦力作用行程(m)。

弹丸炸药装药膛内所受离心加速度较大，但在炸药装药均质且与弹体紧密配合条件下，炸药装药膨胀变形较小，其侧壁与弹体间挤压力较小；其次，膛内过程中炸药装药某处侧壁在某时刻可能与弹体碰撞、产生瞬间大挤压力，但此时产生的侧壁摩擦力持续时间短、行程小，对于做功产热贡献较小。故计算时仅考虑炸药装药底部与弹体间的摩擦力做功产热。

假设膛内炸药装药底面所受弹体轴向压强p均匀分布，而摩擦力及其作用行程互相耦合，需要在炸药装药底面上取圆环微元进行积分，得到

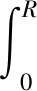
(2)

式中：R为装药底面半径(m)；ω为膛内炸药装药与弹体相对角速度(rad/s)；r为圆环微元的内径(m)。

(2)式去掉积分符号，化简得

(3)

炸药装药底面面积S=πR2，代入(3)式，得

(4)

由整个炸药装药底面所受轴向力(F=pS)产生的摩擦力做功等效行程为

(5)

则炸药装药底面摩擦力做功产热为

(6)

1.3 装药底层温度计算模型

模型假设如下：

1)热传导至装药的部分热量只会在装药底部特征厚度内传导；

2)炸药尚未开始化学反应；

3)热传导过程为一维平面问题，且瞬间完成；

4)热传导过程中，炸药和弹体的密度、比热容、热传导系数均为常数；

5)弹体内部为密闭空间，不考虑热量向装药- 弹体系统外耗散。

热传导至装药的部分热量为

Qc=KQ，

(7)

式中：Qc为装药与弹体摩擦产生的热传导至装药的部分热量(J)；K为热量在装药与弹体间分配系数[14]，由材料物理参数决定。

热量与温度关系为

Qc=c·m·(Tc-Tr)，

(8)

式中：c为炸药装药比热容(J/(kg·K))；m为热传导影响的底层炸药质量(kg)；Tc为膛内装药底层炸药温度(℃)；Tr为环境温度(℃)。热传导影响装药底部的特征厚度[14]约10 μm，故有

m=10-5ρS，

(9)

式中：ρ为炸药装药密度(kg/m3)。

联立(6)式～(9)式，得到炸药装药底层温度计算模型为

(10)

分析计算模型(10)式可知：模型中分配系数K、装药半径R、密度ρ、比热容c取决于高速旋转弹丸装药结构；摩擦系数μ与外界温度Tr由实际条件确定。求解膛内炸药装药温度Tc，还需要获取装药底面所受压强p及装药与弹体相对角速度ω.图2所示为炸药装药底层温度计算模型流程示意图。

图2 装药温度计算模型流程示意图Fig.2 Flow chart of charge temperature model

p、ω可通过开展高旋弹丸膛内运动全过程数值模拟获取。下文应用装药温度计算模型(10)式对某大口径高速旋转弹丸在高温50 ℃射击试验中出现的故障进行计算分析。

2 计算实例

高速旋转弹直接装填钝黑铝(DHL)炸药压装药柱，弹体内壁与装药表面涂有以微晶蜡为主要成分的粘结剂。在高温50 ℃条件下射击该弹，某发弹出炮口一段距离后，装药燃爆致使弹丸解体，发生掉弹事故。经排查，故障弹炸药装药燃爆并非由于引信提前作用引发。下面首先开展该弹膛内运动过程数值模拟，获取膛内运动参数，分析弹丸运动状态。

2.1 模型及算法

采用网络划分软件TureGrid建立弹丸各部件有限元模型，其中弹带、炸药装药、身管膛线按真实结构建立，其余部分按质量等效进行简化。装药与弹体间粘结剂厚度可忽略，通过设置装药与弹体间动摩擦系数表征其力学作用。膛内运动过程中弹带将发生大变形，故加密其网格，通过试算确定各部件网格密度，最终建立的弹丸与身管有限元模型如图3所示。

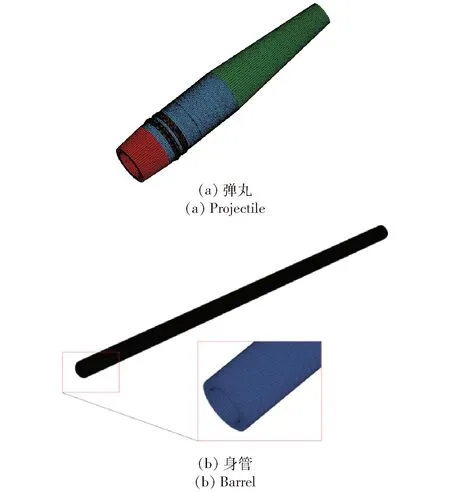
图3 离散化模型Fig.3 Discrete model

采用一般测试方法较难得到弹丸在膛内的速度- 时间曲线，但试验中可测得膛内弹底压力pd与时间t曲线。因此，为计算膛内炸药装药温度上升的边界，获取pd(t)曲线的测试条件为高温强装药。数值模拟采用拉格朗日算法，忽略火药燃气其他影响，在弹底部直接加载试验中获得的膛压曲线pd(t)，计算弹丸膛内运动全过程(从启动到出炮口)。在身管部件上施加固定边界，计算模型如图4所示，图4中标出了加载膛压曲线的区域。

图4 计算模型Fig.4 Computation model

2.2 材料模型

数值模拟中所有部件材料模型均采用各向同性硬化与随动硬化混合模型。

根据Cowper-Symonds模型，动态屈服应力为

(11)

采用应变失效准则，当单元应变达到预设失效应变fs时，单元失效并被程序自动删除，通常取

εr=ln(1+ε0)，

(12)

(13)

式中：εr为材料断裂时真实应变；ε0为参考应变；ζ为模型失效真实应变放大系数。

表1列出了数值模拟中各部件采用的材料参数。

表1 各部件材料参数Tab.1 Material parameters of components in simulation

2.3 计算工况

高速旋转弹丸采用以微晶蜡为主体的粘结剂[15]，在常温下呈固体，与炸药具有较好的亲合力，与钢的摩擦系数约0.2.当外界温度超过50 ℃(含)时粘结剂将出现软化和融化现象，与钢的粘结力较常温下降80%～90%，此时摩擦系数设为0.02.

考虑不同外界温度下装药与弹体处于不同摩擦状态。表2设置了5种工况，其中工况1设置装药底部与弹体为理想无摩擦状态以作对照；工况2对应高温环境；工况3对应装药底部、侧壁和弹体处于不同摩擦条件；工况4介于常温和高温环境；工况5对应常温环境，处于正常摩擦条件。

表2 计算工况Tab.2 List of culcultion conditions

2.4 数值模拟结果

2.4.1 计算结果验证

为验证数值模拟准确性，表3列出了数值模拟与试验实测得到的弹丸出炮口初速与转速。

表3 弹丸出炮口初速与转速Tab.3 Muzzle velocity and rotational speed of projectile

由表3可知：弹丸出炮口初速与转速计算值与试验实测值吻合较好，误差小于5%.

2.4.2 装药与弹体转速

为观测膛内过程装药与弹体的相对运动参数，分别在装药和弹体外表面上取单元A、B作为观测点(见图5)；图6给出了A、B观测点(分别对应装药、弹体)的转速- 时间历程曲线。

图5 0 ms时刻装药与弹体观测点位置Fig.5 Observation points of charge and projectile at 0 ms

从图6中可看出：装药侧壁、底部与弹体的摩擦系数对装药与弹体相对转动状态均有较大影响；装药底部无摩擦时，装药与弹体相对转速最大；高温条件下装药与弹体出现显著相对转动；介于高温与常温时，装药与弹体相对转动不显著；常温条件下装药与弹体基本不发生相对转动。

对比图6(b)、图6(d)及图6(e)可看出：装药与弹体间摩擦系数越小，二者转速差越大，且随时间推移，转速差进一步增大，出炮口时达到最大。从图6(b)中可以看出，高温条件下(摩擦系数为0.02)，出炮口时装药与弹体转速差最大，约为3 000 r/min；从图6(d)中可以看出，介于常温与高温条件下(摩擦系数为0.10)，装药与弹体出现一定转速差；从图6(e)中可以看出，常温条件下(摩擦系数为0.20)，装药与弹体运动状态基本一致，无转速差。

图6 装药与弹体相对转速- 时间历程曲线Fig.6 Rotating velocity-time profiles of charge and projectile body

2.5 装药温度计算参数

依据装药温度计算模型(10)式，不依赖数值模拟的参数包括装药半径R、环境温度Tr、装药密度ρ、装药底部与弹体摩擦系数μ及分配系数K、装药比热容c[16]，如表4所示。

除表4中的参数外，还需要从高速旋转弹丸膛内运动过程数值模拟中获得装药底部压力及装药与弹体相对角速度随时间变化关系。

表4 计算输入参数Tab.4 Input parameters for calculating

数值模拟弹丸膛内运动全过程后，在装药与弹体相应位置上施加观测点，可得到炸药装药底面所受轴向压强p及装药与弹体相对角速度ω，但直接获取的p、ω是一系列散点关系，需要用MATLAB软件拟合为连续曲线，得到其具体函数关系式后，再代入模型中进行积分等运算，拟合得到的p-t、ω-t曲线如图7、图8所示。其中，不同计算条件下装药底部所受弹体轴向压力p基本一致，而装药与弹体相对角速度ω随摩擦条件不同变化较大。

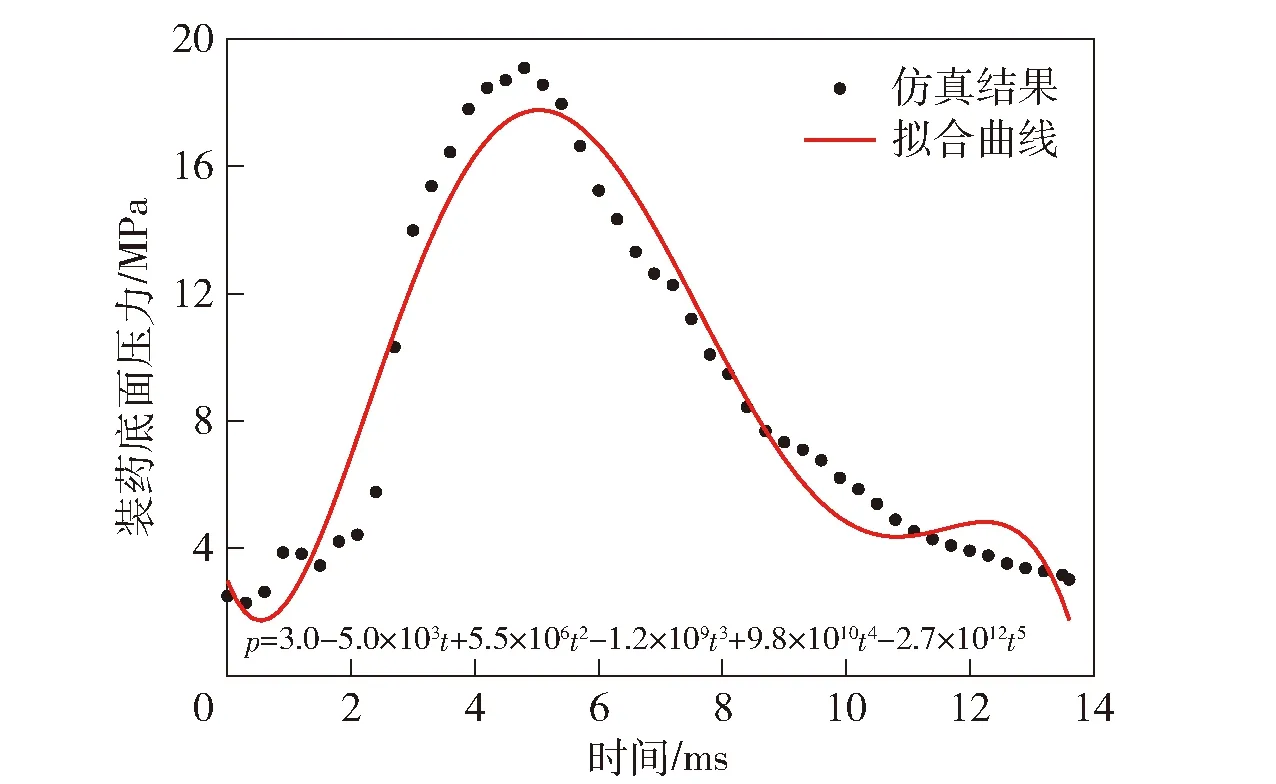
图7 装药底部压力随时间变化关系Fig.7 Pressure-time profiles at the bottom of charge

图8 装药与弹体相对角速度随时间变化关系Fig.8 Relative angular velocity-time profile of charge and projectile body

2.6 装药温度计算结果

利用MATLAB软件将p与ω耦合后进行积分等运算，最终得到不同摩擦条件下炸药装药底层温度随时间变化关系：

1)装药底部与弹体无摩擦时，Tc=50；

2)装药与弹体摩擦系数为0.02时，Tc=-7.83×1016t7+3.39×1015t6-5.21×1013t5+3.3×1011t4-6.51×108t3+7.31×105t2-551t+50；

3)装药侧壁、底部与弹体摩擦系数为0.02、0.10时，Tc=-3.59×1016t7+1.53×1015t6-2.29×1013t5+1.36×1011t4-2.05×108t3+2.08×105t2-81.7t+50；

4)装药与弹体摩擦系数为0.10时，Tc=-4.08×1016t7+1.81×1015t6-2.91×1013t5+2.03×1011t4-5.26×108t3+6.36×105t2-573t+50；

5)装药与弹体摩擦系数为0.2时，Tc=50.

图9所示为根据上述表达式绘制出的膛内装药底层炸药温度随时间变化关系曲线，图9标出了各计算条件下底层炸药出炮口时刻达到的最高温度。

由图9装药温度计算结果可看出：装药与弹体无摩擦时，装药与弹体相对角速度较大，但装药温度无明显变化；装药与弹体摩擦系数较大时，装药与弹体同步转动(ω=0 rad/s)，装药温度亦无明显变化。装药与弹体摩擦系数介于0～0.20时，装药与弹体发生不同程度相对转动，装药温度出现不同程度上升，环境温度达到50 ℃时(摩擦系数为0.02)，炸药装药底层炸药温度最高可达302.3 ℃.

图9 底层炸药温度随时间变化关系Fig.9 Temperature-time profiles of underlying explosive

2.7 分析与讨论

陈力等[16]经过试验和理论分析后指出：对某一特定炸药，尽管起爆手段很多，但炸药起爆的热点温度差别却很小，故在工程应用中可以将炸药的临界起爆温度作为炸药起爆的判据。然而在此次弹丸出炮口一段距离后掉弹事故中，弹丸的炸药装药燃爆并未直接发生在膛内，故不能直接采用炸药临界起爆温度作为判据。

据此，采用DHL炸药热分解温度204 ℃作为参考。装药温度计算结果表明，在高温发射条件下装药底层炸药温度在弹丸出炮口时最高可达到302.3 ℃，远高于DHL炸药的热分解温度。

结合热爆炸理论[17]可知，装药与弹体间的强摩擦首先造成热量在装药表面发生局部沉积，形成大量热点，同时强摩擦产生的热量热传导至装药，致使部分炸药温度上升，当超过炸药热分解温度时，这部分炸药迅速发生热分解，不断产生大量热量和气体。在弹体内部密闭空间内，这些热量和气体无法有效散失，形成的高温、高压环境进一步加速了热点的成长和演化，最终引发炸药装药发生不同等级的爆炸现象(如爆燃、部分爆轰、完全爆轰)，与故障现象(弹丸出炮口一段距离后装药燃爆- 舱体打开- 解体掉弹)相符。