橡胶履带柔性复合材料的本构模型

2020-11-24赵子涵穆希辉杜峰坡

兵工学报 2020年9期

赵子涵，穆希辉，杜峰坡

(1.陆军工程大学石家庄校区弹药工程系，河北石家庄 050003；2.32181部队，河北石家庄 050003)

0 引言

橡胶履带是一种由橡胶基体相和帘线增强相构成的柔性复合材料，近年来在军事领域得到广泛应用，如M113装甲输送车、CV90步兵战车、BvS10装甲全地形车等，都已采用橡胶履带进行作战训练。橡胶履带作为一种橡胶- 帘线复合材料，在服役条件下具有超弹性、大变形和各向异性等力学特性，其性能优劣直接决定了作战保障车辆的使用寿命[1]。因此，建立一种本构模型以准确表征橡胶履带复合材料的力学行为，对于研究其性能和寿命等具有重要的理论意义和工程价值。

国内外学者针对橡胶- 帘线复合材料提出了许多模型。Levin等[2]基于代表性体积元法建立了橡胶- 帘线复合材料数值模型，但代表性体积元阵列难以真实反映材料微细观构造，在预测剪切、弯曲等性能时误差较大。Ren等[3]在Mooney-Rivilin模型基础上推导了包含帘线材料的拉伸模量修正公式，但该模型在预测其他性能时效果较差。Cho等[4]基于加强筋模型建立了橡胶- 帘线有限元模型，但采用加强筋模型需要对橡胶与帘线材料性能进行单独考虑，从而忽略了二者之间的相互作用关系；陈洪月等[5]将橡胶基体简化为线弹性材料，建立了钢丝绳芯橡胶输送带本构模型。

基于纤维增强连续介质力学理论[6]的各向异性本构模型，能够较好地反映大变形和非线性等材料特性，近年来学者们围绕该理论提出了许多适用于橡胶- 帘线复合材料的本构模型。Peng等[7]建立了一种适用于轮胎的各向异性超弹性本构模型，并提出一种参数识别方法；Yang等[8-9]建立了一种具有双向帘线的橡胶- 帘线本构模型。谈炳东等[10]以短纤维增强三元乙丙橡胶包覆膜为研究对象，将应变能解耦为各向同性部分和各向异性部分；但该模型忽略了橡胶与帘线间的作用，当帘线偏角大于45°时模型预测效果较差。黄小双等[11]和郭国栋等[12]对Peng等[7]的模型进行改进，分别考虑剪切作用、法向作用和应变率效应等因素，进一步提高了模型的准确性和应用范围。刘海健等[13]建立了一种适用于粒子分离器鼓包的橡胶- 帘线本构模型。

近年来，为解决橡胶履带横向刚度不连续的问题，国外提出了偏置帘线铺设形式[14-16]，以改善履带横向剪切应力分布。但国内尚无相关研究用于指导橡胶履带的工程设计。此外，目前在橡胶履带式车辆性能分析[17-19]中大多基于线弹性或各向同性理论对橡胶履带进行简化，难以准确反映其真实力学行为。针对此问题，本文开展不同帘线偏角的橡胶- 帘线复合材料单轴拉伸试验研究，分析帘线偏角对材料力学性能的影响。基于纤维增强连续介质力学理论建立一种橡胶- 帘线超弹性模型，并提出一种基于粒子群优化算法和牛顿迭代法的模型参数寻优拟合方法。最后，利用Abaqus软件的UANISOHYPER_INV子程序验证所建模型在有限元分析中的适应性和正确性。

1 试验研究

1.1 试样制备

橡胶履带以硫化橡胶为基体材料，根据不同部位的性能要求采用不同胶料配方。履带中铺设有钢丝帘线作为加强层，用于承受车辆牵引力。花纹内部沿履带宽度方向铺设有玻璃纤维棒。橡胶履带基本结构如图1所示。

图1 橡胶履带结构示意图Fig.1 Structure diagram of rubber track

由图1可知，橡胶履带中钢丝帘线嵌入帘线胶中。因此，橡胶- 帘线复合材料试样以帘线胶为基体材料，以钢丝帘线为增强材料。试验所用试样由青岛开世密封工业有限公司生产，试样长度为145 mm(其中标距段长度为95 mm)，宽度为25 mm，厚度为2.9 mm，帘线所占体积比约为0.11.定义履带长度方向为0°，分别制备帘线铺设角度为0°、15°、45°、60°、90°的试样。帘线偏角定义如图2所示。

图2 帘线偏角示意图Fig.2 Schematic diagram of cord off-axis angle

1.2 单轴拉伸试验

利用美国Instron公司生产的5982型万能材料试验机对橡胶- 帘线试样进行单轴拉伸试验。由于试样在拉伸过程中变形速率较快，为防止损坏引伸计，采用南京中迅微传感技术有限公司生产的PMLAB非接触式测量系统测量试样变形。试验测试系统如图3所示。

图3 单轴拉伸试验测试系统Fig.3 Test system for uniaxial tension experiment

为消除Mullins效应对试验结果的影响，对试样进行预处理，即重复进行加载- 卸载循环，每次加载位移为5 mm，直至最后两次循环曲线基本相同。设置拉伸速率为50 mm/min，该条件下试样应变率约为5.75×10-3s-1.试验时，调整双目相机拍摄频率，使其与拉伸速率相匹配。

1.3 试验结果分析

为消除预加载后橡胶- 帘线试样产生的残余变形，对试验数据进行数据处理，得到不同帘线偏角下试样的单轴拉伸试验数据，如图4所示。

图4 不同帘线偏角下试样的单轴拉伸试验数据Fig.4 Uniaxial tension data with different cord off-axis angles

由图4可以看出，不同帘线偏角下橡胶- 帘线复合材料的力学性能并不相同。对于指应变条件下的橡胶- 帘线复合材料，当帘线偏角较小时，帘线偏角对材料力学性能的影响较为显著，其拉伸模量和拉伸强度随帘线偏角的增大而减小；当帘线偏角较大时，帘线偏角对材料力学性能的影响逐渐减小。根据应力传递理论，在单轴拉伸载荷作用下，橡胶基体首先受到力的作用，然后通过一定方式传递到帘线或橡胶- 帘线界面上。当帘线偏角较小时，与橡胶材料相比，帘线材料具有较大的拉伸模量，此时帘线是主要承载结构；当帘线偏角较大时，应力传递规律被破坏，帘线的主导作用降低，因此材料力学性能的变化不够显著。

2 橡胶- 帘线复合材料本构模型

2.1 本构模型一般形式

橡胶履带是一种单向纤维增强复合材料，根据Spencer等[6]提出的纤维增强复合材料理论，其应变能函数W可以表示为关于右Cauchy-Green应变张量C不变量和帘线初始方向向量a0的各向同性函数，如(1)式所示：

W=W(C,a0)=W(I1,I2,I3,I4,I5)，

(1)

(2)

将橡胶- 帘线复合材料应变能解耦为橡胶变形产生的应变能Wm、帘线拉伸产生的应变能Wf以及橡胶与帘线相互作用产生的应变能Wf，m.因此，应变能函数W可写为(3)式：

W=W(C,a0)=Wm+Wf+Wf，m.

(3)

σ=J-1FSFT=2{W1B-W2B-1+I4W4a⊗a+
I4W5(a⊗Ba+Ba⊗a)}-pI，

(4)

式中：Wi=∂W/∂Ii，i=1，2，3，4，5；F为变形梯度张量；B=FFT为左Cauchy-Green应变张量；a为当前构形中帘线方向单位向量；p为静水压力；I为2阶单位张量。

2.2 橡胶应变能函数

通常橡胶应变能函数可分为两大类[21]：一类是基于连续介质力学的唯象模型，如Neo-Hookean模型、Mooney-Rivlin模型等；另一类是基于热力学统计方法的分子链网络模型，如Arruda-Boyce模型等。为便于模型参数拟合，一般选择基于不变量的唯象模型表征橡胶材料。不同的本构模型都具有相应的适用范围[22]，因此应当根据具体的橡胶材料试验数据来确定橡胶应变能函数形式。

2.3 帘线应变能函数

将帘线视为不可压缩材料，即处于压缩状态的帘线应变能为0.帘线的应变能与其拉伸情况相关，因为I4等于帘线方向拉伸率λf的平方，故一般将其应变能函数定义为关于I4-1的多项式[23-24]或指数函数形式[9]。为便于模型参数拟合，本文定义帘线应变能函数Wf[20]为

(5)

式中：k1、k2和k3为材料参数(MPa)。

2.4 橡胶与帘线相互作用应变能函数

橡胶与帘线相互作用产生的应变能Wf，m可利用基体法向与帘线方向的夹角φ表示[20]为

Wf，m=f(I4)(mtan4φ+ntan2φ)，

(6)

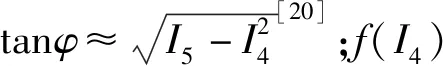
f(I4)=exp[l(I4-1)]，

(7)

式中：l为无量纲材料参数。

3 模型参数拟合与验证

3.1 橡胶应变能函数参数拟合

帘线偏角为90°的单轴拉伸试验数据可近似作为纯橡胶材料单轴拉伸试验数据[25-26]，试验结果如图5所示。该拉伸条件下，总应变能W等于橡胶变形产生的应变能Wm，即Wf=Wf，m=0.因此，由(4)式可得

(8)

式中：σi(i=1,2,3)为主应力；λi为对应的主伸长率。

单轴拉伸时，有σ1=σ(σ为名义应力)，σ2=σ3=0 MPa.分别采用Yeoh模型、Mooney-Rivlin模型和2阶多项式模型对试验数据进行拟合，结果如图5所示。其中，各模型表达式为

图5 帘线偏角为90°时单轴拉伸试验数据与拟合结果Fig.5 Test data and fit curves of 90° off-axis tension

Yeoh模型：

Wm=C10(I1-3)+C20(I1-3)2+C30(I1-3)3，

(9)

式中：C10、C20、C30为材料参数(MPa)。

Mooney-Rivlin模型：

Wm=C10(I1-3)+C01(I2-3)，

(10)

式中：C01为材料参数(MPa)。

2阶多项式模型：

Wm=C10(I1-3)+C01(I2-3)+C20(I1-3)2+
C02(I2-3)2+C11(I1-3)(I2-3)，

(11)

式中：C02和C11为材料参数(MPa)。

由图5分析可知，2阶多项式模型对试验数据的拟合效果最好。因此选用2阶多项式模型表征橡胶基体材料，模型参数C10、C01、C20、C02分别为C10=-87.899 0 MPa，C01=94.341 4 MPa，C20=1 662.885 4 MPa，C02=2 508.631 1 MPa，C11=-4 025.691 0 MPa.

3.2 帘线应变能函数参数拟合

利用帘线偏角为0°的单轴拉伸试验数据进行帘线应变能函数的参数拟合。在该拉伸条件下，总应变能W等于橡胶变形产生的应变能Wm和帘线拉伸产生的应变能Wf之和，且拉伸应变ε与不变量I4间存在如下关系式：

(12)

根据(12)式，可由帘线偏角为0°的单轴拉伸应力- 应变曲线(见图6)建立(I4-1)-Wf关系。采用最小二乘法进行参数拟合，得到帘线应变能函数参数k1、k2和k3分别为0.023 8 MPa、4.841 9 MPa、989.355 8 MPa.

图6 帘线偏角为0°时单轴拉伸试验数据与拟合结果Fig.6 Experimental data and fit curve of 0° off-axis tension

3.3 橡胶与帘线相互作用应变能函数参数拟合

利用帘线偏角为15°的单轴拉伸试验数据进行橡胶与帘线相互作用应变能函数的参数拟合。该拉伸条件下，总应变能W包括橡胶变形产生的应变能Wm、帘线拉伸产生的应变能Wf以及橡胶与帘线相互作用产生的应变能Wf，m.由(4)式可得

(13)

式中：α为帘线偏角。

由于σ1=σ，σ2=σ3=0 MPa，由(13)式可得

(14)

(14)式包含未知量λ1～λ3、l、m和n.为确定参数l、m和n的值，提出一种基于粒子群优化(PSO)算法和牛顿迭代法的参数寻优算法[27-28]，其基本流程如下：

1)设置初始参数。因为待求参数为l、m和n，所以第i个粒子的位置xi表示为

xi=[xi1,xi2,xi3]，

(15)

则种群数量为N的粒子群X表示为

X=[x1,x2,…,xN].

(16)

设定种群数量N=30，学习因子c1=c2=2，最大迭代次数M=100，每个粒子的位置分量变化范围均为[-20,20]，速度变化范围均为[-2,2]。

2)对于某一粒子，即给定参数l、m和n时，可根据牛顿迭代法计算得到λ2和λ3.粒子的适应度函数F如下：

(17)

式中：r为试验数据个数；σcj为名义应力计算值；σtj为名义应力测试值。F的值越趋近于1，表明粒子的适应度越好。

3)根据(15)式计算每个粒子的适应度，并更新个体最优值pi和全局最优值g.

4)根据(16)式和(17)式更新粒子位置xi和速度vi：

xi(t+1)=xi(t)+vi(t+1)，

(18)

vi(t+1)=
vi(t)+c1[pi-xi(t)]+c2[g-xi(t)].

(19)

5)当达到最大进化次数M后停止迭代，否则返回步骤2进行新一轮迭代。

采用PSO-牛顿迭代法，得到橡胶与帘线相互作用的应变能函数参数l、m以及n分别为7.832 6、-1.389 0 MPa、0.325 9 MPa.

帘线偏角为15°时单轴拉伸数据、拟合与仿真结果如图7所示。

图7 帘线偏角为15°时单轴拉伸数据、拟合与仿真结果Fig.7 Test data,fit and simulation curves of 15° off-axis tension

3.4 本构模型验证

根据(5)式、(6)式和(11)式以及拟合所得模型参数，可以得到橡胶- 帘线复合材料本构模型。为验证该模型的正确性，分别对帘线偏角为45°和60°的单轴拉伸试验进行预测，结果如图8和图9所示。由图8和图9可以看出，模型预测结果与试验数据趋势基本一致，决定系数R2分别为0.992 8和0.982 9，预测效果较为理想。

图8 帘线偏角为45°时单轴拉伸试验数据、预测与仿真结果Fig.8 Test data,prediction and simulation curves of 45° off-axis tension

图9 帘线偏角为60°时单轴拉伸试验数据、预测与仿真结果Fig.9 Test data,prediction and simulation curves of 60° off-axis tension

4 模型仿真应用验证

为考察本文所提像胶- 帘线复合材料本构模型在有限元仿真中的适用性，并进一步验证模型的正确性，基于该模型，利用Abaqus软件UANISOHYPER-INV接口定义材料属性，分别对帘线偏角为15°、45°和60°的单轴拉伸试验工况进行数值仿真。

根据试样尺寸和试验条件建立仿真模型，其中夹持一端采用固定约束，另一端沿拉伸方向设置位移载荷。根据应变量设定不同的拉伸位移，得到仿真应力云图如图10所示。提取应力和应变仿真结果与试验数据进行对比(见图7～图9)。提取不同帘线偏角下试样的横向刚度仿真结果，结果如图11所示，并计算其平均值和方差，如表1所示。

表1 不同帘线偏角下试样横向刚度的平均值和方差Tab.1 Mean and variance of lateral stiffness of specimens with different off-axis angles

图10 不同帘线偏角下试样的单轴拉伸仿真结果Fig.10 Simulated results of specimens with different off-axis angles

图11 不同帘线偏角下试样横向刚度的仿真结果Fig.11 Lateral stiffnesses of specimens with different off-axis angles

由图7～图9可见，仿真结果与试验数据趋势基本一致，最大仿真误差分别为5.05%、10.86%和8.79%，在可接受范围内。分析误差产生的原因主要有以下4点：1)由图8和图9可以看出，基于帘线偏角为90°、0°和15°单轴拉伸数据拟合得到的模型参数在预测帘线偏角为45°和60°试验数据时存在应力值偏大的现象，使用该模型及其参数定义材料属性时，势必将此误差引入有限元仿真中。2)橡胶材料具有Mullins效应，虽然在试验前对试样进行了预加载等处理，但仍无法完全消除其影响；而本文模型没有考虑橡胶材料的Mullins效应，因此基于该模型的有限元仿真无法完全反映试样实际变形情况。3)为消除预加载产生的残余变形，需要对试验数据进行数据处理，这也会引入一定误差。4)为避免出现不收敛问题，对有限元模型进行了一定程度的简化，例如采用固定约束将夹具与试样固联。但在实际试验时，虽然采取涂抹松香等措施，夹具与试样间仍存在轻微滑移。

结合单轴拉伸试验数据分析图10、图11和表1可知，对于指定应变条件下的橡胶- 帘线复合材料，当帘线偏角较小时，橡胶- 帘线复合材料的拉伸强度和纵向刚度较大，横向刚度均值较小且波动较大，此状态下应力主要沿帘线方向分布，帘线偏角对橡胶- 帘线复合材料的变形影响较大。随着帘线偏角逐渐变大，橡胶- 帘线复合材料的拉伸强度和纵向刚度减小，而横向刚度趋于稳定且均值逐渐增大，此状态下应力分布较为均匀。由上述分析可以看出，当应变条件一定时，帘线偏角大小是影响橡胶- 帘线复合材料拉伸强度和刚度的关键因素，合理设计橡胶履带的帘线偏角能够使其在提供足够纵向拉伸强度的同时，保持较好的横向刚度稳定性，从而提高橡胶履带性能。

此外，通过仿真结果与试验数据的对比分析表明，本文建立的橡胶- 帘线复合材料本构模型能够较好地应用于有限元仿真，也为下一步开展橡胶履带式装备的有限元分析研究奠定了基础。