完善认知结构,强化知识运用
2020-11-23钱程毛月华
钱程 毛月华
摘要:整理反思课不仅要帮助学生巩固和进一步理解所学知识,而且要帮助学生沟通知识之间的内在联系,使所学知识进一步条理化和系统化。为此,需要引导学生理清知识脉络,沟通内在联系,强化知识运用,并激发学生进一步“生长”的活力。
关键词:整理反思课联系练习《立体图形的表面积和体积》
作为小学数学总复习课的一种重要课型,整理反思课不仅要帮助学生巩固和进一步理解所学知识,而且要帮助学生沟通知识之间的内在联系,使所学知识进一步条理化和系统化。为此,需要引导学生理清知识脉络,沟通内在联系,强化知识运用,并激发学生进一步“生长”的活力。
《立体图形的表面积和体积》整理反思课是基于苏教版小学数学六年级下册《总复习》单元相应内容的《整理与反思》栏目和《练习与实践》栏目第1—第7题设计的。本节课基本的教学目标是:(1)理解并掌握立体图形表面积、体积的意义以及计算方法和推导过程,能够应用表面积和体积的计算方法解决相关的实际问题;(2)经历整理的过程,沟通知识之间的内在联系,体会过程中蕴含的思想方法,使所学知识进一步条理化和系统化;(3)进一步体会知识整理的价值,积累相应的数学活动经验,提高学习数学的兴趣和学好数学的积极性。根据整理反思课的目标定位和操作要点,本节课的教学过程如下:
一、记忆唤醒,激活认知经验
师在小学数学学习中,我们认识了很多图形,从点到线,再到平面图形、立体图形。今天这节课,我们要复习立体图形的有关知识。前面我们已经复习了立体图形的特征,想一想:我们还可以从立体图形的哪些方面进行复习?
生立体图形的表面积和体积。
师好的,接下来就让我们一起开启今天的复习之旅吧。
二、知识梳理,完善认知结构
(一)理清知识脉络
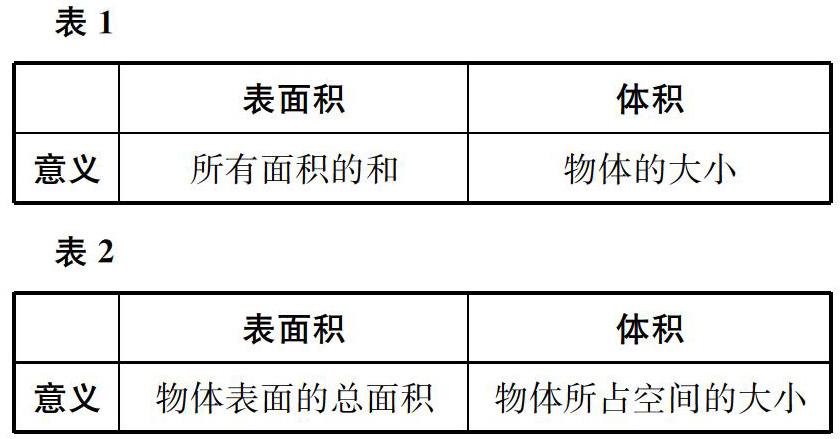
师课前,我们已经从意义、单位和方法三个方面自主整理了表面积与体积的区别。我们先来看意义上的不同。(出示表1、表2)这是两位同学整理的结果,你觉得哪种表述更加规范?
生第2种。
师也就是说,表面积是指物体表面的总面积,而体积是指物体所占空间的大小。说到物体的体积,我们还可以很自然地想到容器的容积,谁来介绍一下容积?
生容器所能容纳物体的体积叫作容器的容积。
师你认为体积和容积有什么相同点和不同点?
生它们都是指所占空间的大小,它们的计算方法相同,计量单位一样;但是,计算体积需要测量外部数据,计算容积需要测量内部数据。
生任何物体都有体积,但不一定有容积。
师说得真好!接着,我们再来看表面积和体积的单位有什么不同,谁来说一说?
生常见的表面积单位有平方米、平方分米、平方厘米,体积单位有立方米、立方分米、立方厘米。
师对啊!那相邻的两个单位之间的进率又是多少呢?
生相邻的两个表面积单位之间的进率都是100,而相邻的两个体积单位之间的进率都是1000。
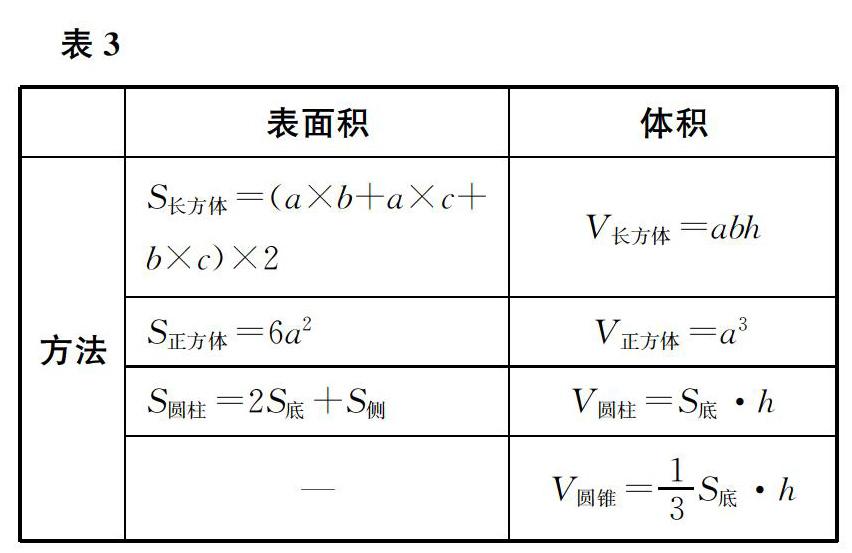
师表面积和体积除了意义、单位不同,计算方法也不同,它们分别是怎么计算的呢?
(学生口答,教师记录,得到表3。)
[评析:知识的回顾整理不是简单的“重复昨天的故事”,而是对原先知识的“再学习”。因此,课前,教师用预习单引导学生对立体图形的表面积、体积(容积)的意义、单位、计算方法等进行自主整理。这样的活动,可以帮助学生将脑海中原有的知识按照一定的体系有序地提取出来。而后,课堂上的交流、对比或补充,可以帮助学生加深对立体图形表面积、体积(容积)的理解,明晰知识之间的联系与区别。]
(二)沟通内在联系
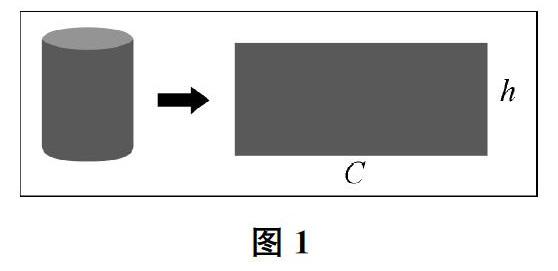
师说得很完整!那圆柱的底面积和侧面积分别又是怎么计算的呢? 我们又是怎么推导圆柱侧面积的計算方法的呢?
生S底=πr2,S侧=Ch。圆柱侧面沿高剪开是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,长方形的面积等于长乘宽,所以,圆柱的侧面积等于底面周长乘高。
师是这样吗?(课件演示,得到图1)能把知识背后的原因说得这么清楚,真了不起!其实,不仅圆柱存在侧面积,长方体和正方体也存在侧面积。你认为长方体和正方体的侧面积应该怎么计算?
生把前后左右四个面的面积加起来。
师老师赞同你的想法,再想一想:还有没有更加直接的方法?
生底面周长乘高。把长方体或正方体的侧面展开,也可以得到一个长方形,长方形的长等于底面周长,长方形的宽等于高,所以,长方体或正方体的侧面积也可以用底面周长乘高来计算。
师(课件演示,得到图2)看来,不管是圆柱、长方体,还是正方体,都能用底面周长乘高来计算侧面积。
[评析:这一环节侧重对立体图形侧面积概念和计算方法的拓宽与联系。首先,从圆柱侧面积的计算方法出发,抛出“长方体、正方体的侧面积应该怎么计算”的问题,启发学生基于“侧面的面积”的含义得到长方体、正方体侧面积的概念,生成长方体、正方体侧面积的自然计算方法。其次,利用一组动画演示,帮助学生发现长方体、正方体的侧面积也可以用底面周长乘高来计算,从而统一侧面积的计算公式。整理反思课的魅力就在于此:不是简单地堆砌知识,而是找出不同知识之间的联系,构建新的知识,掌握新的方法。]
师那么,这些立体图形的体积计算公式及其推导过程又是怎样的呢?接下来,请同学们四人一组,每人选择一个立体图形,互相说说它的体积计算公式及其推导过程。
(学生交流。)
师哪一组来给大家介绍一下?
生长方体的体积计算公式是“长×宽×高”。其推导过程是把长方体分成若干个小正方体,长方体的长决定了每排可以分几个,宽决定了可以分几排,高决定了可以分几层,小正方体的个数是每排的个数乘排数乘层数,而有多少个小正方体就表示这个长方体的体积是多少,所以,长方体的体积是长乘宽乘高。
生正方体的体积计算公式是棱长的立方。由于正方体是特殊的长方体,所以,其推导过程与长方体是一样的。
师的确,我们可以根据长方体的体积公式进一步推导出正方体的体积公式,那圆柱呢?
生圆柱的体积公式是“底面积×高”。其推导过程是沿着圆柱的底面直径切开,拼成一个近似的长方体,圆柱的体积等于长方体的体积,圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高,长方体的体积可以用底面积乘高,所以圆柱的体积也可以用底面积乘高。
师你们同意吗?
(学生表示同意。)
师也就是说,我们根据长方体的体积公式进一步推导出了圆柱的体积公式。
生圆锥的体积公式是“底面积×高×13”。它是通过实验推导出来的:准备等底、等高的圆柱和圆锥形容器各一个,将圆锥形容器装满水,再倒入圆柱形容器中,发现只能倒到容器的13处。
师也就是说,我们通过圆柱的体积公式又进一步推导出了圆锥的体积公式。你们同意这一组的想法吗?把掌声送给这一组。
(学生鼓掌。)
[评析:这一环节侧重对立体图形体积计算方法的联系。学生在五年级《多边形的面积》单元的回顾整理中,进行过多边形面积公式之间的对比联系,具备了画联系图的经验。因此,教师放手让学生以小组为单位进行汇报,在交流互动中不断完善认识。]
师刚才的回顾整理,我们经历了怎样的过程?
生首先,复习了表面积和体积的意义、单位和计算方法三个方面的区别;然后,进一步复习了表面积和体积的计算公式以及推导过程,并发现了它们之间存在的一些联系。
师(完成板书,得到图3)刚才,我们在不知不觉中得到了一棵“知识树”。其实,围绕数学上的任一知识,都可以像这样“生长”出很多关联的知识,而且可以设计出很多不同的样子。课前,同学们也进行了自主整理。通过今天的学习,相信同学们一定都有了新的想法。课后,大家可以再试着理一理、画一画,并与之前的整理比一比。
[評析:课前基于已有的认知经验,进行了初步的梳理;课内在师生、生生交流中,形成了较为系统的知识结构(“知识树”);课后再次进行自主整理,并与原来的整理结果进行对比。由此,学生可以感受到知识不断清晰、由“点”连成 “线”再结成“网”的过程。]
三、练习提升,强化知识运用
师今天,我们复习的是立体图形的表面积和体积。其实,很多立体图形都可以由平面图形创造出来,(出示图4)请看活动要求。
(学生阅读要求。)
师要求都明确了吗?请按照要求开始探究。
(学生探究。生成的学习资源有:①绕着长方形的宽转;②绕着三角形较短的直角边转;③绕着长方形的长转;④绕着三角形较长的直角边转;⑤折成长为5 cm、宽为1 cm、高为3 cm的长方体;⑥折成长为4 cm、宽为2 cm、高为3 cm的长方体;⑦折成棱长为3 cm的正方体;⑧沿着长方形的长卷; ⑨沿着长方形的宽卷。)
师(同步出示学习资源①②)他们分别创造出了怎样的立体图形?分别是通过怎样的方式创造出来的?
(学生口答。)
师尽管他们选择了不同的图形,但都是绕着较短的那条边转的。创造出来的这两个立体图形有什么联系吗?
生等底、等高,圆柱的体积是圆锥的3倍。
师(出示学习资源③)同样是选择长方形纸,还有同学是这样转的,你有什么发现吗?
生这是绕着长方形的长转的。不管是绕着长转,还是绕着宽转,我发现侧面积不变。
师观察得真仔细!怎么转才能使得到的圆柱的表面积和体积更大一些呢?
生绕着宽转。
师(同步出示学习资源②④)同样是用三角形纸转,也可以得到不同的圆锥,那怎样转体积更大呢?
生也是绕着较短的直角边转。
师(同步出示学习资源⑤⑥⑦)这些长方体是怎么创造出来的?你觉得这些长方体都应该符合什么要求?
生它们都是沿着长折出来的,折出来的长与宽的和都是6 cm,高都是3 cm。
师是的。继续观察,你还有什么发现吗?
生侧面积都相等,都等于长方形纸的面积;长和宽越接近,表面积和体积就越大。
师同学们真的很善于观察!其实,除了像这样沿着长折,我们还可以沿着宽折。沿着长折和沿着宽折又有什么联系和区别呢?聪明的你课后去想一想,一定会有所发现的。
师(同步出示学习资源⑧⑨)我们还可以通过卷一卷,创造出不一样的圆柱。比较这两种卷法,你有什么发现?
生侧面积一样,而且与折一折创造出的长方体的侧面积相同,都等于长方形纸的面积,都可以用长方形纸的长乘宽计算。
生我还发现,沿着长卷得到的圆柱体积和表面积更大。
师确实,刚才同学们用同样的长方形纸和三角形纸创造出了不同的立体图形,它们之间存在着一定的联系。数学学习就应该像这样,同中求异、异中求同,在变与不变中找到相应的规律。
[评析:整理反思课中的练习是帮助学生进一步完善知识结构的重要纽带,也是发展学生数学能力的重要环节。本环节以一道习题作为学生进一步“生长”的落脚点。通过转一转、折一折、卷一卷等操作,学生不仅摆脱了枯燥练习的枷锁,而且很好地发展了自身的创造能力。多层次的交流,还将知识点的复习融入其中:在“转一转”的交流中复习等底、等高圆柱与圆锥体积之间的关系;在“转一转”“折一折”“卷一卷”的交流中反复体会图形中的“变与不变”——体积在变而侧面积不变,对图形之间联系的认知向纵深发展。]
四、拓展延伸,激发“生长”活力
师(出示图5)咱们再来看这4个立体图形。如果让你把这4个立体图形分分类,你会怎么分?依据又是什么?
生根据面的特征分成长方体、正方体,圆柱、圆锥。
生根据体积公式分成长方体、正方体、圆柱,圆锥。
师长方体、正方体、圆柱的体积都可以用底面积乘高来计算。我们还可以发现,它们存在着相同的特征:上下两个面完全相同,上下粗细完全一样。像这样的立体图形称为直柱体。(出示图6)这里的三棱柱、五棱柱也属于直柱体,猜猜看:它们的体积可以怎么计算?
生底面积乘高。
师究竟是不是这样呢?我们一起来看一看。(播放视频)果然,就如同学们猜的那样,直柱体都可以用底面积乘高来计算体积。关于直柱体的体积,有兴趣的同学课后可以继续研究。
[评析:学生经过“理—联—练”,已经能够将本节课复习的知识连成“线”、结成“网”,对知识的理解也具有了一定的深度。而这一环节的拓展,让本节课的回顾整理进一步深入。首先,让学生发现长方体、正方体、圆柱的共同特征,引出直柱体的概念;其次,让学生猜想、了解三棱柱、五棱柱等直柱体体积的计算方法,使学生的思维更加开阔,令本节课的学习余音绕梁。]
参考文献:
[1] 潘小福.小学数学教材的专业化解读[M].南京:江苏凤凰教育出版社,2017.
[2] 潘小福.课型范式与实施策略:小学数学[M].南京:江苏教育出版社,2012.
