针阔混交林林分结构与固碳功能耦合关系研究——以青羊湖国有林场马尾松—南酸枣混交林为例

赵东方

(国家林业和草原局中南调查规划设计院，长沙 410014)

耦合是近年来应用频率较高的专业术语之一，已逐渐应用于农业、生物学、生态学和地理学的研究。将耦合引入到林业研究领域具有重要的创新意义，它强调了因素之间深层次的关系[1]，为揭示森林系统的协同作用和制约关系提供了理论依据。

森林具有复杂的结构和功能，森林功能的发挥很大程度上取决于森林的结构是否合理。林分结构是林木个体生长发育空间的决定性因素[2]，直接影响林分稳定性、林木质量、健康状况及林分多种功能，是森林经营过程中最可能调节的因素，因此，优化林分结构是培育多功能森林的重要途径。合理的林分结构，既有利于林木个体获取充分的生长发育条件，又能实现土地和空间最大限度利用，还具有培育优良干形、提高产量和提升木材品质等重要意义[3]。

目前，国内学者对林分结构与功能的耦合关系进行了一些研究，但大多是对林分非空间结构与功能进行研究，对林分空间结构与林分功能之间的耦合关系的研究鲜见报道。对于林分结构与水源涵养功能[4-7]、土壤养分[8-9]等耦合关系的研究较多，但尚未有对林分空间结构与非空间结构和固碳功能的耦合关系进行研究。本文以马尾松(MassonPine)—南酸枣(Choerospondiasaxillaris)人工混交林为研究对象，通过主成分分析法研究林分结构与固碳功能之间的关系，建立耦合关系模型，以期为针阔混交林可持续经营及合理的经营密度提供参考。

1 研究区概况

青羊湖国有林场位于湖南省宁乡县西部，平均坡度35°，最高海拔927.4m，最低海拔166m；林场内土壤以山地黄红壤、山地黄棕壤为主，土层厚度40～100cm，腐质层厚度18～28cm，土壤肥力较高；中亚热带向北亚热带过渡的大陆季风性湿润气候区，年均气温16.2℃，平均降雨量1438.8mm，相对湿度85%，无霜期273d。林场土地总面积为1129.1hm2，森林覆盖率为98.7%。

林场内物种多样，共有木本植物86科691种。有银杏(Ginkgobiloba)、南方红豆杉(Taxuschinensis)、水杉(Metasequoiaglyptostroboides)等5种国家一级重点保护植物；有香榧(Torreyagrandis)、鹅掌楸(Liriodendronchinese)等15种国家二级重点保护植物。

2 材料与方法

2.1 样地设置与调查

在青羊湖国有林场选择马尾松林、马尾松—南酸枣混交林，设置16块大小为25m×25m的固定标准地。样地基本调查因子包括海拔、坡度、坡位、坡向、土壤类型、土层厚度，林木的X，Y坐标、乔木树种组成、年龄、株数、胸径、树高、冠幅、郁闭度等因子。样地基本概况详见表1。

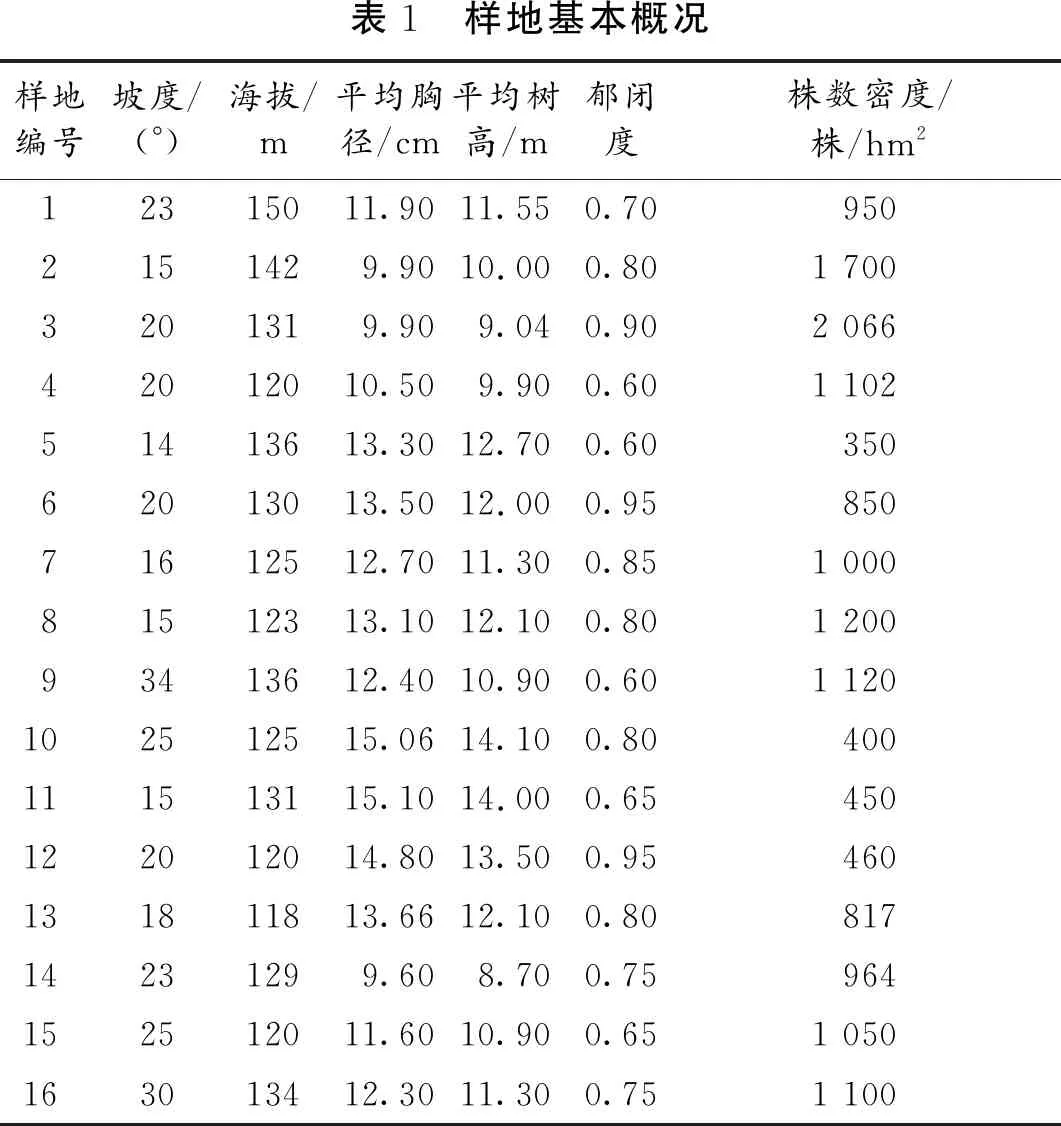
表1 样地基本概况样地编号坡度/(°)海拔/m平均胸径/cm平均树高/m郁闭度株数密度/株/hm212315011.9011.550.709502151429.9010.000.801 7003201319.909.040.902 06642012010.509.900.601 10251413613.3012.700.6035062013013.5012.000.9585071612512.7011.300.851 00081512313.1012.100.801 20093413612.4010.900.601 120102512515.0614.100.80400111513115.1014.000.65450122012014.8013.500.95460131811813.6612.100.8081714231299.608.700.75964152512011.6010.900.651 050163013412.3011.300.751 100

2.2 研究方法

2.2.1 耦合关系因子的确定

选取林分平均胸径(X1)、平均高(X2)、郁闭度(X3)、树种组成(X4)、林分密度指数(X5)等作为林分非空间结构指标；选取混交度(X6)、角尺度(X7)、大小比数(X8)、林层指数(X9)、竞争指数(X10)、开阔比数(X11)等作为林分空间结构指标[10-11]；选取灌木盖度(X12)、灌木均高(X13)、草本盖度(X14)、草本均高(X15)等以反应林下植被情况。

2.2.2 固碳功能

依据马尾松、硬阔及软阔单木生物量模型[12]，计算样地单位面积生物量，换算到样地单位面积的固碳量，计算公式如(1)：

(1)

式中，C为单位面积固碳量；i为第i株树；wi为第i株树的生物量；A为样地面积。

2.3 数据处理及分析

采用SPSS 19.0软件，运用主成分分析法，通过降维从众多因子中找出主要的影响因子，用较少的林分结构变量来衡量林分的固碳功能，以此来研究林分结构与固碳功能之间的耦合关系。

为验证改进后的遗传算法在排课问题中的应用效果，与文献[10]及基本遗传算法进行对比实验。种群数量设为400，基本遗传算法迭代数设为500，本文改进的遗传算法最大允许停滞代数设为20，交叉概率为0.89，变异概率为0.02。分别在不同授课任务数时，三种算法得到的平均运行时间及适应度值如图所示。

3 结果与分析

3.1 主成分提取与表达

将代表林分结构因子的角尺度、大小比数、混交度、开敞度、林层指数等指标中的属性数据转换为数值型数据，将数据标准化，消除数量级和量纲的影响，然后，计算其相关矩阵，结果如表2所示。

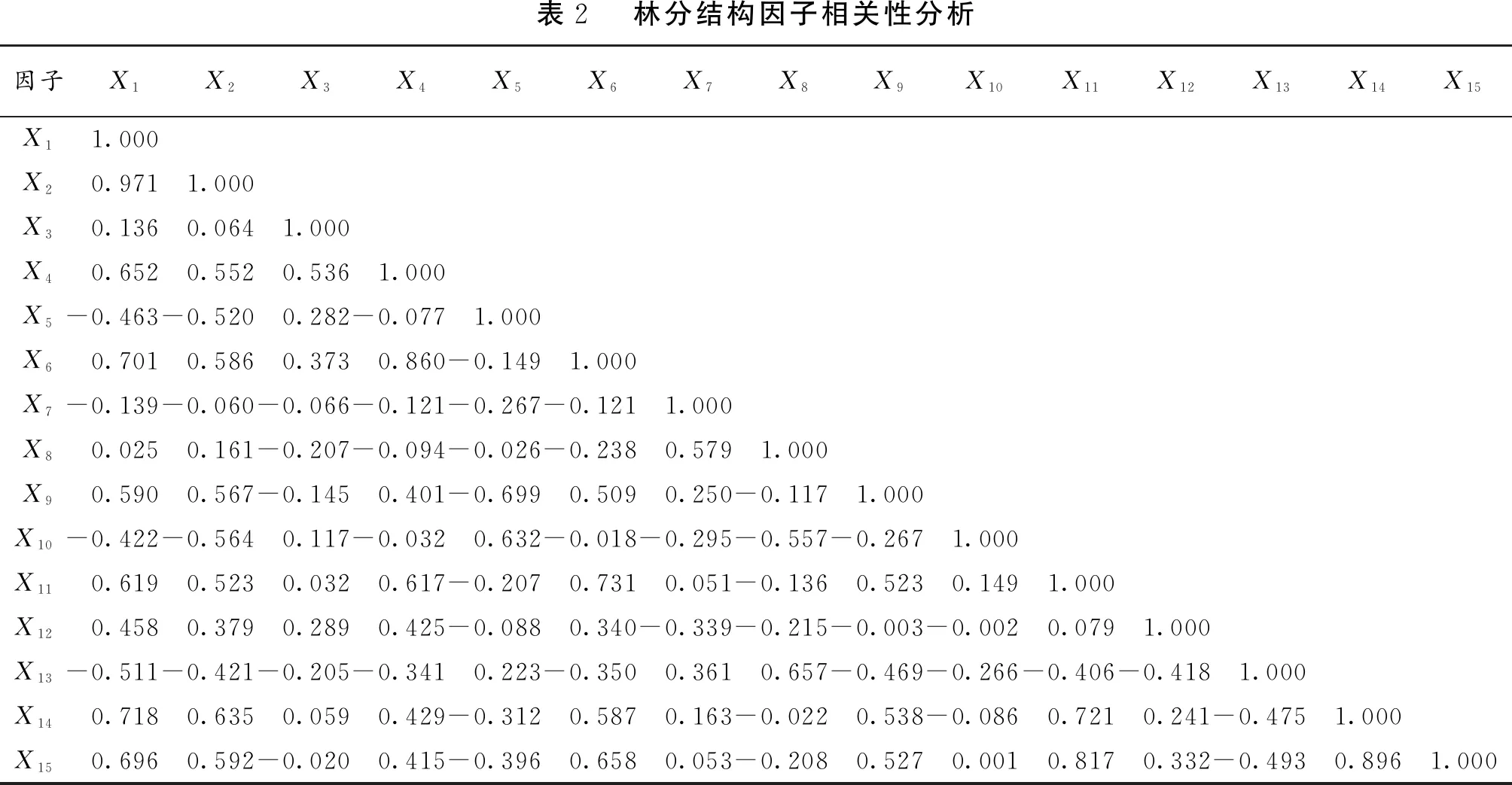
表2 林分结构因子相关性分析因子X1X2X3X4X5X6X7X8X9X10X11X12X13X14X15X1 1.000 X20.971 1.000 X30.136 0.064 1.000 X40.652 0.552 0.536 1.000 X5-0.463 -0.520 0.282 -0.077 1.000 X60.701 0.586 0.373 0.860 -0.149 1.000 X7-0.139 -0.060 -0.066 -0.121 -0.267 -0.121 1.000 X80.025 0.161 -0.207 -0.094 -0.026 -0.238 0.579 1.000 X90.590 0.567 -0.145 0.401 -0.699 0.509 0.250 -0.117 1.000 X10-0.422 -0.564 0.117 -0.032 0.632 -0.018 -0.295 -0.557 -0.267 1.000 X110.619 0.523 0.032 0.617 -0.207 0.731 0.051 -0.136 0.523 0.149 1.000 X120.458 0.379 0.289 0.425 -0.088 0.340 -0.339 -0.215 -0.003 -0.002 0.079 1.000 X13-0.511 -0.421 -0.205 -0.341 0.223 -0.350 0.361 0.657 -0.469 -0.266 -0.406 -0.418 1.000 X140.718 0.635 0.059 0.429 -0.312 0.587 0.163 -0.022 0.538 -0.086 0.721 0.241 -0.475 1.000 X150.696 0.592 -0.020 0.415 -0.396 0.658 0.053 -0.208 0.527 0.001 0.817 0.332 -0.493 0.896 1.000

由各个因子的相关系数可知，林分结构因子间存在一定的相关性，各个因子相互作用，相互影响。使用因子分析来将信息简化，筛选出影响林分结构和功能的代表性因子。通过主成分因子分析法计算每个主成分因子的特征值和贡献率(表3)。由表3可知，前4个主成分的样本方差累积贡献率为 81.034%，大于80%，符合主成分提取原则，因此，这4个主成分因子能够代表所研究的马尾松—南酸枣混交林的林分结构特征。

另外，各主成分因子的代表变量，即主成分体现的结构因子的信息，可以从因子载荷矩阵表中(表4)获得。由各因子载荷的绝对值可知，第1主成分在林分的平均胸径、平均高、混交度、草本盖度和草本均高等指标上有较大载荷；它们的载荷分别为0.923，0.843，0.826，0.821和0.847。第2主成分在林分的大小比数和竞争指数指标上有较大载荷，它们的载荷分别为0.758和-0.791。第3主成分在林分的郁闭度和树种组成指标上有较大载荷，它们的载荷分别为0.618和0.460。第4主成分因子主要反映了林分的角尺度和开阔比数特征，它们的载荷分别为0.514和0.460。

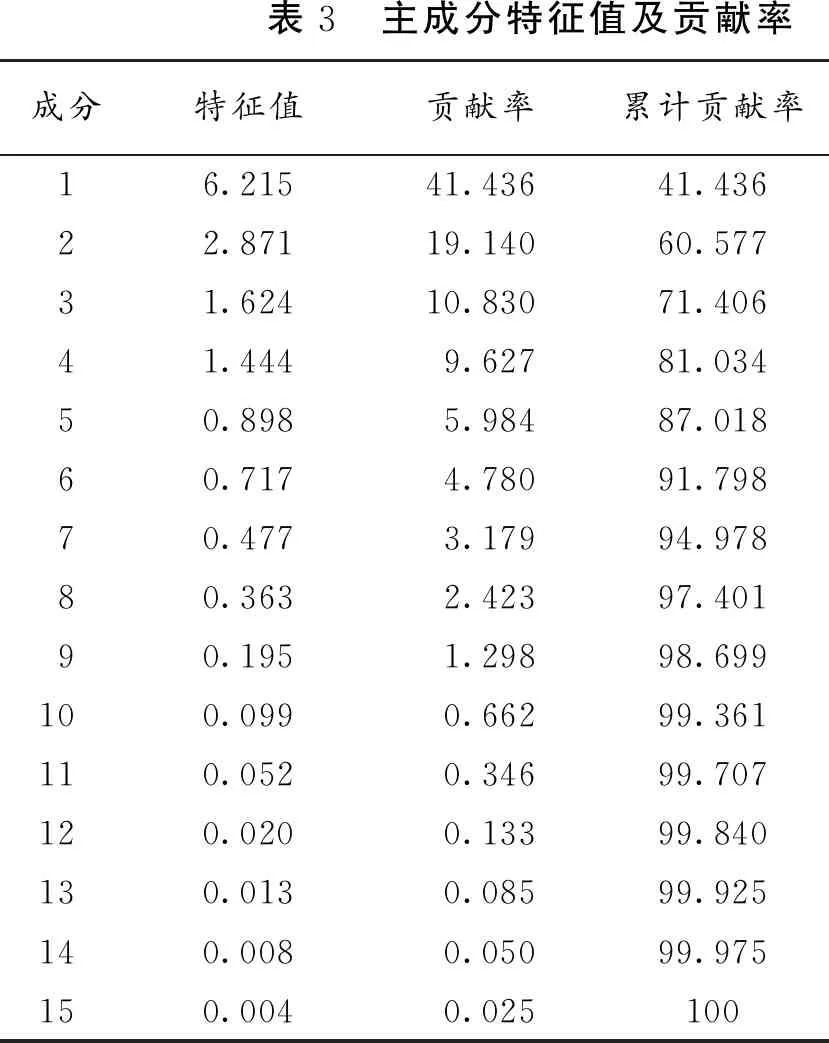
表3 主成分特征值及贡献率成分特征值贡献率累计贡献率16.21541.43641.43622.87119.14060.57731.62410.83071.40641.4449.62781.03450.8985.98487.01860.7174.78091.79870.4773.17994.97880.3632.42397.40190.1951.29898.699100.0990.66299.361110.0520.34699.707120.0200.13399.840130.0130.08599.925140.0080.05099.975150.0040.025100

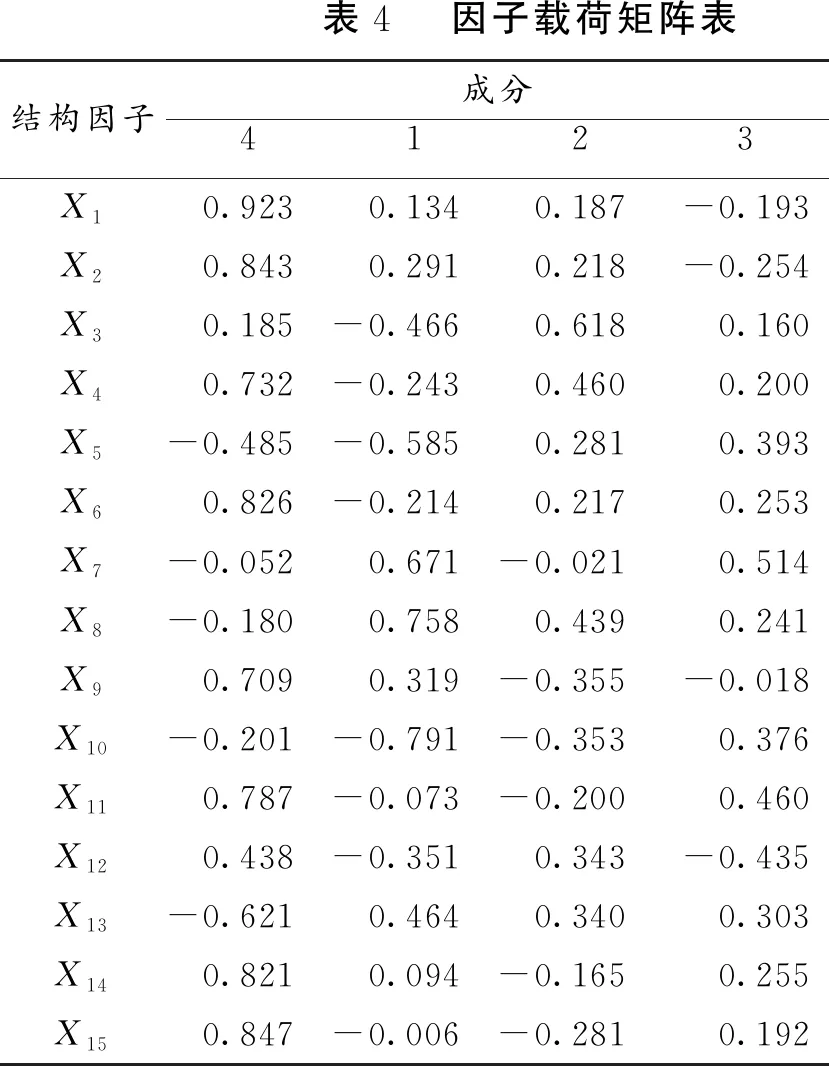
表4 因子载荷矩阵表结构因子成分1234X10.9230.1340.187-0.193X20.8430.2910.218-0.254X30.185-0.4660.6180.160X40.732-0.2430.4600.200X5-0.485-0.5850.2810.393X60.826-0.2140.2170.253X7-0.0520.671-0.0210.514X8-0.1800.7580.4390.241X90.7090.319-0.355-0.018X10-0.201-0.791-0.3530.376X110.787-0.073-0.2000.460X120.438-0.3510.343-0.435X13-0.6210.4640.3400.303X140.8210.094-0.1650.255X150.847-0.006-0.2810.192

3.2 耦合关系模型构建

根据对林分结构特征的分析结果，将其与林分固碳功能指标对应，运用SPSS19.0采用Pearson检验法进行结构因子与功能指标的相关性分析，并对其进行模型拟合。

根据林分结构因子与林分固碳功能的特点，选择线性模型拟合林分结构与固碳功能之间的关系，表达式如(2)：

A=m1x1+m2x2+…+mnxn

(2)

式中:A为因变量；x1，x2，…,xn为自变量；m1，m2，…,mn为自变量系数。可以从因子得分系数矩阵(表5)获得自变量系数m的值。

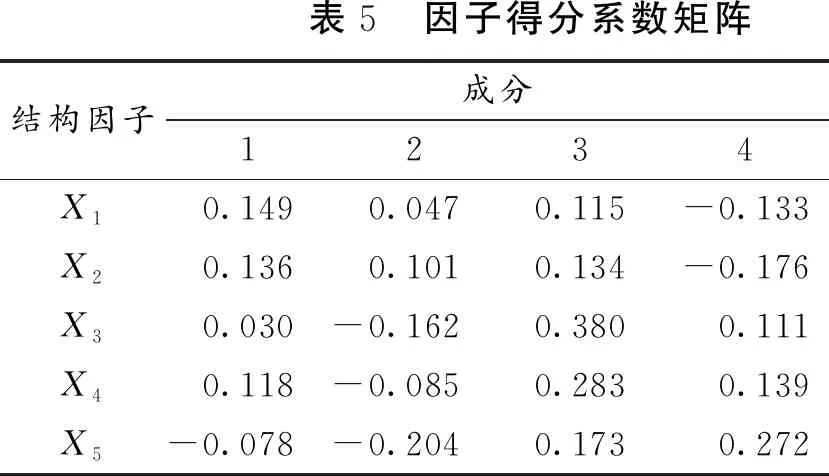
表5 因子得分系数矩阵结构因子成分1234X10.1490.0470.115-0.133X20.1360.1010.134-0.176X30.030-0.1620.3800.111X40.118-0.0850.2830.139X5-0.078-0.2040.1730.272

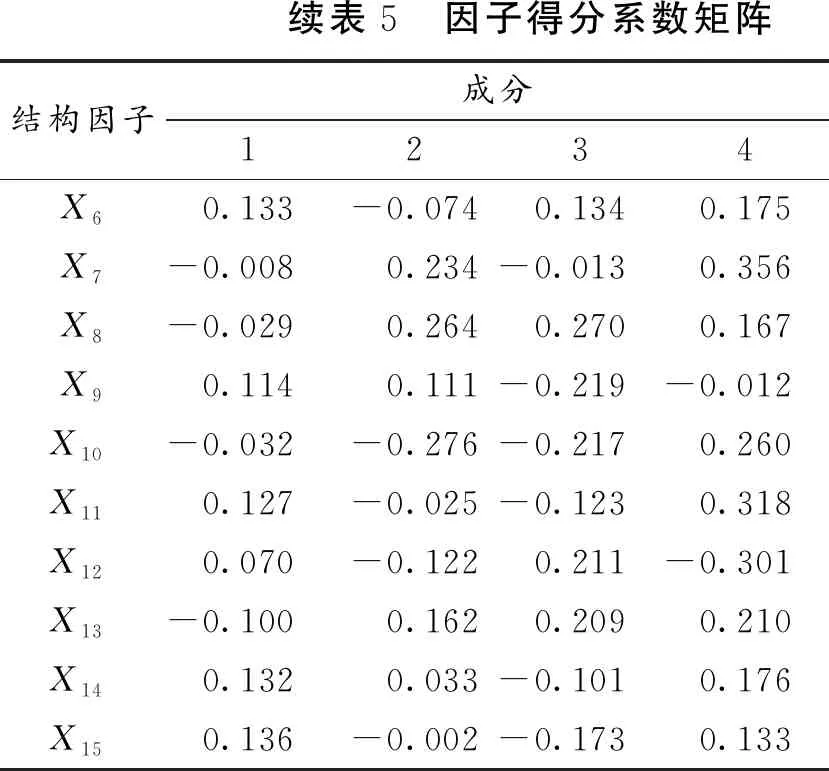
续表5 因子得分系数矩阵结构因子成分1234X60.133-0.0740.1340.175X7-0.0080.234-0.0130.356X8-0.0290.2640.2700.167X90.1140.111-0.219-0.012X10-0.032-0.276-0.2170.260X110.127-0.025-0.1230.318X120.070-0.1220.211-0.301X13-0.1000.1620.2090.210X140.1320.033-0.1010.176X150.136-0.002-0.1730.133

基于因子得分系数和原始变量的观测值来计算出各个样地在4个主成分上的得分，如(3)～(6)式所示：

(3)

F2=0.047X1+0.101X2-0.162X3-0.085X4-0.204X5-0.074X6+0.234X7+0.264X8+0.111X9-0.276X10-0.025X11-0.122X12+0.162X13+0.033X14-0.002X15

(4)

F3=0.115X1+0.134X2+0.38X3+0.283X4+0.173X5+0.134X6-0.013X7+0.27X8-0.219X9-0.217X10-0.123X11+0.211X12+0.209X13-0.101X14-0.173X15

(5)

F4=-0.133X1-0.176X2+0.111X3+0.139X4+0.272X5+0.175X6+0.356X7+0.167X8-0.012X9+0.26X10+0.318X11-0.301X12+0.21X13+0.176X14+0.133X15

(6)

3.3 因子得分综合分析

每个主成分因子的权重(主成分特征值)和因子得分乘积之和便是主成分因子综合得分(F)，即林分的固碳功能指数，表达式如(7)：

(7)

式中:λ1=6.215，λ2=2.871，λ3=1.624，

λ4=1.444。

通过建立的林分结构与功能模型可以计算出16个样地的固碳功能指数。为方便样地等级划分，将各样地的主成分因子综合得分值F进行标准化。标准化后的值用P表示，P即为评价指数，范围在0～100之间。其标准化公式为：

(8)

式中：Fi表示第i个样地的固碳功能综合评价值；Fmin表示样地固碳功能的最小综合评价值；Fmax表示样地固碳功能的最大综合评价值。

利用分析评价结果构建的公式计算样地主成分综合评价指数P，根据综合评价指数P和蓄积量的关系散点图(图1)可以看出，它们之间的关系可以用线性函数表达，其相关系数为0.801 7(P<0.05)。

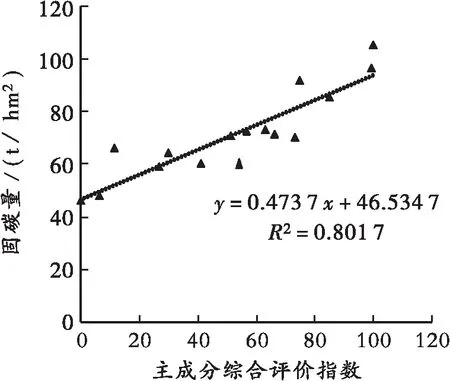
图1 主成分综合评价指数与蓄积量相关关系散点图

通过16个样地功能评价值P的计算结果可知：固碳功能评价值最高达100分(1个样地)，主林层是马尾松与南酸枣，次林层为木荷(Schimasuperba)、香樟(Cinnamomumcamphora)等树种，林分结构合理；固碳功能综合评价值在[80，100)的样地有2个，主要优势树种是南酸枣、木荷；固碳功能综合评价值在[60，80)分的样地有4个；固碳功能综合评价值在[40，60)分的样地有4个；固碳功能综合评价值在[20，40)分的样地有2个；固碳功能综合评价值低于20分的样地有3个，其树种全部为马尾松，林层结构单一。

4 结论与讨论

1)研究结果表明，运用主成分分析研究林分固碳功能与结构因子的关系是可行的。通过寻找影响林分固碳功能的主要结构因子，再通过降维将代表林分结构的15个因子简化为4个，从分析结果看，影响林分固碳功能的结构指标可以归并为林木和林下植被生长情况、林木竞争压力、树种组成、空间分布格局4个方面。其中林木和林下植被生长情况的贡献率最高，对林分固碳功能的影响最大。

2)本研究以青羊湖林场马尾松—南酸枣混交林为研究对象，建立了林分结构与固碳功能的耦合关系模型，利用模型计算出各样地主成分综合评价指数P，从P与固碳功能(蓄积量)之间的关系散点图(图1)可知，两者具有显著相关关系，其中综合评价指数最高的样地其蓄积量也最高，固碳综合评价指数较高的林分其密度约为1050株/hm2、郁闭度为0.65左右，林层结构为复层林的马尾松—南酸枣混交林。该类型林分有利于保持较稳定的林分结构特征和较高的固碳功能，是青羊湖林场马尾松—南酸枣混交林的最佳林分结构。

3)影响林分固碳功能的因子是多方面的，固碳功能的大小是由多个因子相互作用、共同影响的结果，这是由森林生态系统所具有的复杂结构和功能特征决定的。为了最大限度地发挥林分的固碳功能，就要确保林分结构的合理性，只有结构合理才能正常发挥其功能[13]。研究区可以制定科学的经营管理措施，调整林分结构，最大限度地发挥其经济效益。

4)在构建林分结构与固碳功能的耦合关系模型时，选择了与林分固碳功能密切相关的15个结构指标，但选择的指标还不够全面，林地的土壤养分、土层厚度等也会对林木固碳产生影响，因此，今后的研究还需进一步探讨这一方面的内容。本研究采用了线性模型来表达林分结构与功能之间的关系，而非线性模型也会成为今后的研究方向之一。