哲学角度下的微积分

苏志勇 张飞羽

（兰州大学数学与统计学院，甘肃 兰州 730000）

微积分学是以实数理论为基础，以极限为工具，来研究函数的分析性质，即连续性、可微性和可积性的理论，其中蕴涵着丰富的辩证思想和美妙和谐的表现方式.明白有限与无限、常量与变量是对立统一的，可利用有限和常量分别描述、处理无限和变量，体现了哲学对数学的指导意义.

1 有限与无限

黑格尔说：“真正的无限并不仅仅是超越有限，而且包括有限并扬弃有限于自身内.”我们说，有限与无限是对立统一的，有限能描述刻画无限，无限可指导有限.微积分内容中几乎所有的概念或定义都是由极限这个概念来定义的，而函数的极限涉及到两个无限，即自变量的无限（变化）过程和对应的函数值的无限变化.人的认识是无限的，但实践是有限的.如果不把我们认识到的无限用有限来描述和刻画，就无法把握其概念的本质和内涵，自然也就无法发展和应用.这里关于极限定义的柯西语言是一个很好的示范，它用一系列的有限∀ε ＞0 及δ ＞0，刻画了两个无限ax → 和.)(Axf→据此，我们了解了极限收敛的本质（常用几何意义揭示）以及其属性（即唯一性、局部有界性和局部保号性）.微积分学定义了许多无限（无穷），其公式为：

无限=有限+极限.

例如，比较直观的是级数、无穷积分等的定义.极限的伟大意义就在于：把我们认识到的无限（或蕴含无限思想之概念）无须转化成可实践的有限，就可利用极限直接对其严格定义、计算、应用，如切线、曲率、几何体的度量等概念.现举例说明.

解此类题的切入点是依题意（条件）将无穷区间分成有限区间和条件约束区间后再分别处理［1］.另外，“数学归纳法”和“有限覆盖定理”也是联系有限与无限的桥梁.

通过对微积分课程的学习，我们也许有以下相应的公式：

无界=有界+极限，变量=常量+极限，精确=近似+极限.

2 局部与整体

函数的极限、连续、可导、可微等都是局部概念，所属性质也称为局部性质，即在给定点的附近来讨论函数性质的.例如，局部保号性、局部有界性、极值、曲率、隐函数的存在性等等.而有界、可积、一致连续、一致收敛、凸性、单调性等都是整体概念，所属性质可称为整体性质，即在给定的数集（特别是区域）上来讨论函数性质的［2］.例如，最值问题、实数连续性基本定理、微分积分中值定理等.因此，在讨论具体问题时，首先要分清是局部性质还是整体性质，然后利用各自的属性进行讨论，要特别注意两者之间的关系和桥梁（转换）.现举例说明.

局部与整体是对立统一的.例如，我们在讨论幂级数在收敛区间上的连续性、可导性时，采用了在点的邻域内构造小闭区间的方法，将局部问题转化成整体问题，然后利用幂级数的内闭一致收敛性得到证明.同样，隐函数存在定理的证明，也是利用了局部性质与整体性质的转换.另外，“区间套原理”将区间上的属性转移到点的局部，以及“有限覆盖定理”可将区间上每一点的局部性质综合起来转化成区间上的整体性质，更是体现了局部与整体的辩证关系［3］.

例3 利用区间套原理（或有限覆盖定理）证明闭区间上的连续函数有界.（略证）

比较直观地体现局部与整体关系的内容有：闭区间上连续函数的性质、泰勒公式、微分积分中值定理、单调区间与极值点、凹凸区间与拐点等等.

3 具体与抽象

数学是以抽象的形式，追求高度精确和可靠的知识.不仅概念抽象，而且其方法亦然.与抽象性相联系的数学的另一特点是，在对自然界和人类社会的探索中追求最大限度的一般模式和算法.从数学的发展史来看，处处彰显着特殊与一般的辩证关系.以微积分为例，从极限概念的建立开始，各种形式的微分积分定义以及各类级数概念的建立，都是从具体事例出发，利用极限进行了从量变到质变的过程，然后抽象到一般.以定积分为例：从“计算曲边梯形的面积”出发，经过：①分割闭区间，将整体问题局部化；②在局部以直代曲，以常量代替变量；③做和，用近似代替精确；④取极限，从量变到质变等过程后，抽象成定积分定义.注意：这里的量变到质变涵盖：有限到无限、有界到无界、常量到变量、近似到精确等等.

顺便提一下，另一寓意下的特殊与一般.例如，关于初等函数连续性的论述，以及其导数公式，就是以三至四个基本初等函数为讨论对象，具体证明了它们的连续性，以及求得其导数公式，再根据“连续和可导这两种函数属性经过四则运算、复合运算和反转运算保持不变”，从而获得了一般初等函数的连续性和导数公式.

具体与抽象是对立统一的.因为对具体的深入认识才能更好地抽象，因为抽象而能更好地把握具体.在微积分学理论中，同样的内容，随着目的或要求的不同，具体与抽象的概念也在转换.例如，我们有时将函数表示成幂级数是为了便于求极限，或近似计算，或建立数学用表；反之，我们又希望求出幂级数的和函数，以了解其几何特征，或分析性质.

在“微积分”一些内容的教与学中，把具体与抽象的关系视为实与虚之关系，可加深对这些内容和所用方法的理解.例如，在计算方程（实在）决定的函数（虚拟）的导数时，我们“虚拟”了该函数参与相应的运算和理论推导，只要在结论中没有该函数的“身影”，那么，所用方法就是成功的.著名拉格朗日乘数法，就是虚拟了条件关系的隐函数，将条件极值问题转化为无条件极值来处理，利用关系式消去表达式中隐函数的偏导数而得，这种思想手段有点像做辅助线.

4 常量与变量

微积分学的任务就是研究函数，而函数则是变量与变量之间的一种关系.有时我们无法把握变量，需要借助于常量，特别是运用“可在局部以直代曲，以常量代替变量”的思想.而常量这一概念可广义化，如直、平、平均、常规等等.据此我们建立了积分理论，也严格定义了切线、曲率等概念.反之，在解决具体问题时，需要我们化常量关系为变量关系，实际上就是归结成一个函数问题.例如，在计算一些数项级数和时，将其转换成函数项级数，利用导数与积分运算的互逆性求出和函数而得之.类似地还有，二元泰勒公式的证明、施瓦兹不等式的证明、一些椭圆积分的计算等等.特别值得一提的是，定积分的变上限手段.偏导数概念、含参积分理论、微元法思想等，更是体现了常量与变量的辩证关系.

5 内容与形式

黑格尔说：“内容既在其自身中具有形式，同时形式对于内容也是一种外在的东西，……，存在着内容与形式的相互转化.”我们说，内容决定形式，形式是内容的表现.从数学的角度来看，恰当的形式有助于内容的应用与发展.例如，积分符号的设制，给积分内容中命题论证和计算提供了极大的方便，可以说是内容与形式完美结合的典范.

另一方面，对不同内容，探索其本质，用同一形式表现，更是对内容的深刻反映.例如，在用柯西语言表示函数极限的收敛时，依据自变量的七种变化过程，相应有柯西语言的七种表示形式，这七种表示形式可归结为一个形式：

lim X=A ⇔∀ε ＞0,∃时刻T ，T 之后，有||X-A ＜ε.

上式将极限的收敛性聚焦于时刻的存在性.

综观数学的创造与发展，形式化语言和模式相当普遍，如代数学、几何学等.四元数、非欧几何的创造与发展就是典型.那么在微积分中，我们是不是也从这个角度来看一下呢?例如，记yx ΔΔ ,分别是自变量的改变量与函数值的改变量，考察下列情形：

6 一元与多元

在微积分学里，“一”与“二”是有本质区别的.例如，相对于一元函数，二元函数不再有单调、反函数等概念；“二”与“多”没有本质区别，所以对多元函数的研究，主要以二元函数为主.进一步，对二元成立的结论，特别是一些（不）等式，可直接推广到相应的多元形式；当然，“多”与无穷是有本质区别的［4］!

怎样利用一元函数的理论来研究多元函数呢？常见的有以下几种方法：

（1）累次法.即转化成若干个一元函数的问题，做累次处理.例如，多元函数的微分积分中值公式、重积分计算、多元函数的极值和复合函数的链式法则等.

（2）折线法.即将所讨论的有关点用直线或折线连接起来，在其上构造一元函数来讨论问题.例如，多元函数的中值定理及泰勒公式的证明、用第二类曲线积分计算原函数等.

例5 证明二元函数的泰勒公式.

（3）统一符号法.在表达方式上采用统一的符号，可将一元函数的一些成果直接平行地转移到多元函数方面.例如，极限、连续性、可微性、泰勒公式等.一般情况下，只要是关于局部问题的讨论，都可考虑该法.

例6 试建立二元函数的泰勒公式.

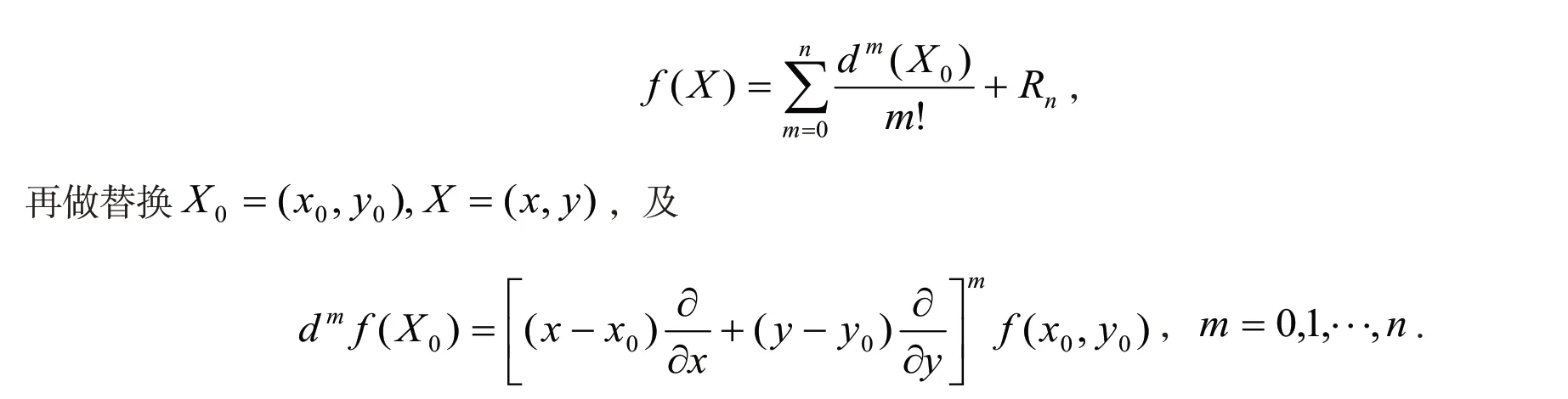
（4）变量替换法.对一些特殊的多元函数，通过变量替换直接化成一元函数的形式.

反过来，利用多元函数的理论来研究一元函数，可解决许多问题.例如，隐函数存在定理的论证、含参积分理论的建立、讨论由方程决定的一元函数的分析性质、极值、凸性等.

7 创造与重复

数学是人类精神世界的产物，可以说是天才们“凭空”创造的.数学史就是创造与重复的历史.“微积分”课程一般分成两部分：一元函数微积分学和多元函数微积分学.显然，无论从形式还是概念与方法方面来看，前者是创造，后者是重复.当然，前者蕴含着重复，后者蕴含着创造.上面第6节展示的就是这种关系的一点细节.关于重复，柏拉图、尼采等哲学家赋予了深刻内涵，并分成若干层次.我们在这里暂停留在第一层面：重复就是重复.比较直观的案例就是在解决具体问题时，某一方法的累次使用.常见的此类方法如：洛必达法则、微分中值定理、导数与单调等.例如，利用洛尔定理证明：若区间上n 阶可导函数有n+1个零点，则其n 阶导数必有零点.一般情况下，命题中只要有关键词函数、导数、高阶导数可考虑这类方法.