关于代数系统的挖补定理

谢祥云

（五邑大学数学与计算科学学院，广东 江门 529020）

何为挖补？顾名思义就是挖去一块再补上一块.譬如，我们穿的一件衬衫（A），发现胸部口袋（B）坏了，当然B 是A 的一个部分，是“原装”.现在我们要修补，找一块和B 大小材料以及颜色一样的布料C 将B 替换下来，这样我们就得到了一件修补好的衬衫D，当然D 已经不是原来的A 了，但它非常像A 可以看作“高仿”，这高仿过程中当然离不开B 和C.这样的例子我们在代数学中有类似的类比案例，那就是代数学中的挖补定理.我们清楚，挖补只是一个形象的说法，能给我们抽象的代数思维留下一个想像的落脚点，实际上它是代数系统同构定理的一部分，这个定理在抽象的代数学同构的构造中扮演着非常重要的角色，张禾瑞编著的《近世代数》教材［1］在环的构造前讲授了该定理，这个定理为后面的分式域的构造，环的构造，多项式分裂域存在及唯一性证明等都起到了非常重要的作用，吴品三教授的近世代数［2］教材中也谈到该定理，但是叙述高度浓缩，学生不容易读懂.卢占会［3］对该定理作了一些推广.遗憾的是后来出版的大量近世代数教材对该定理均做了淡化处理，作为代数学同态定理的一部分教授.作为代数学初学者读懂理解该定理的意义及证明是非常重要的，同学们也很感兴趣那补丁C 是怎么有机的融合到D 中去的？

张禾瑞编著的《近世代数》教材于1978 年出版，是基于读者仅具有高中数学基础的情况下编写的，用的数学语言和现代代数学语言差异很大，学生看不到严格的数学证明，老师在教学中也很难在数学道理上讲明白，本文基于这个目的对挖补定理给了一个新的严格的数学陈述.

为了简单化，本文所说的代数系统均带有两个二元代数运算，文中没有提及的概念等请参看［4-8］.

设A 是一个非空的集合，映射∘:A×A →A 称为集合A 上的二元运算.带有运算（二元或n 元）的集合我们称之为代数系统.需要说明的是对任意元素a,b ∈A，映射∘的像∘(a,b)我们记为a ∘b，有时在不至于混淆的情况下我们直接写成ab.

定义1 设(A,∘)和(B,*)是两个各有一个二元运算的代数系统，φ： A →B 是A 到B 的映射，如果φ 满足：

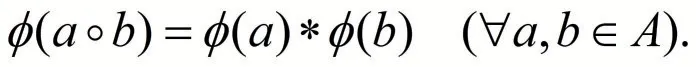
称φ 为代数系统(A,∘)到代数系统(B,*)的同态的映射.

当然我们可以进一步地给出

定义2 设(A,+,×)和(B,⊕,⊗)是两个各有两个二元运算的代数系统，φ： A →B 是A 到B 的映射，如果φ 满足：

称φ 为代数系统(A,+,×)到代数系统(B,⊕,⊗)的同态的映射.

如果φ 是满射，单射和双射我们分别称φ 为满同态映射，单同态映射和同构映射.当φ 为满同态映射或同构映射时，我们称这两个代数系统是同态的或同构的.

从代数系统的定义来看，拥有同样一个承载集的代数系统就有成千上万个，个个都要研究？个个都有用吗？不是的，首先我们关注系统中运算要有良好的性质，那就是运算律，同时也要关注系统内部不同运算之间的关联；其次我们通过同构这一个工具对系统作一个分类，也即将“几乎一致”的系统归为一类，那什么是几乎一致呢？就是系统的灵魂一致，这就需要我们对不同系统做不同的考究.我们下面考虑环

定义3 一个带有两个二元运算的代数系统(R,+,∘)称为环，如果R 满足：

1） (R,+)是一个加群；

2） (R,∘)是一个半群；

3）对(R,+,∘)中任意三个元素a,b,c ∈R，乘法满足对加法的左右分配律：

引理4 设(R,+,×)是带有两个二元运算的代数系统，B 是非空集合且集合R 和B 之间有一个双射φ 存在，那么可以在B 上定义两个二元运算⊕和⊗使得代数系统(R,+,×)和代数系统(B,⊕,⊗)同构.

证明 首先我们需要在集合B 上构建两个二元运算.对B 任意的两个元素a,b ∈B，定义：

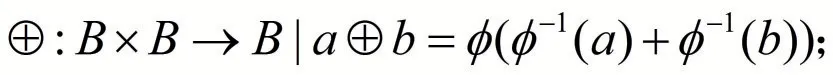
由于映射φ 是双射，不难看出对B 两个元素a,b ∈B，a⊕b 和a ⊗b 都是唯一的，即⊕和⊗均为B上的二元运算.

为了证明φ 是这两个代数系统的同构，根据定义2，我们仅需要验证：对任意的x,y ∈R ，φ(x+y)=φ(x)⊕φ(y);φ(x×y)=φ(x)⊗φ(y).事实上，根据这两个运算的定义以及双射的性质，我们有

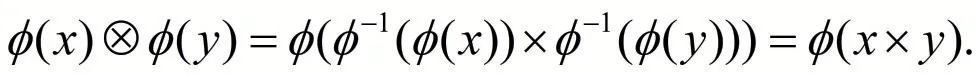
证毕.

反过来，我们还有

引理5 设(R,+,×)是带有两个二元运算的代数系统，B 是非空集合且是φ 集合B 到环R 的双射，那么可以在B 上定义两个二元运算⊕和⊗使得代数系统(B,⊕,⊗)和代数系统(R,+,×)同构.

证明 首先我们需要在集合B 上构建两个二元运算.对B 任意的两个元素a,b ∈B，定义：

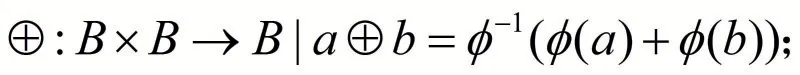
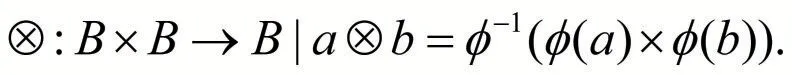
由于映射φ 是双射，不难看出对B 两个元素a,b ∈B，a⊕b 和a ⊗b 都是唯一的，即⊕和⊗均为B上的二元运算.

为了证明φ 是这两个代数系统的同构，根据定义2，我们仅需要验证：对任意的x,y ∈B ，φ(x⊕y)=φ(x)+φ(y);φ(x ⊗y)=φ(x)×φ(y).事实上，根据这两个运算的定义以及双射的性质，我们有

证毕.

我们可以从字面上大致理解什么是同态，即状态相同，或者说系统A 的特征、代数性质沿着箭头方向传送给了B，但是B 的特征一般不能上传；所谓同构就是两个代数系统结构相同，双方的性质，特征可以互传，即你中有我，我中有你！例如，由引理4我们根据［1］中相关的结论容易得出.

引理6 设(R,+,×)是环，B 是非空集合且集合R 和B 之间有一个双射φ 存在，那么我们可以在B上定义两个二元运算⊕和⊗使得(B,⊕,⊗)是环，且环(R,+,×)和(B,⊕,⊗)同构.

有了上述准备后我们给出挖补定理

图1 挖补定理示意图