改进嵌入式容积卡尔曼滤波的锂电池荷电状态估计

杨 莹，王大维，赵为光，孙 健，于天洋

(黑龙江科技大学 电气与控制工程学院，哈尔滨 150022)

0 引 言

电池与电池组已经广泛应用在电动汽车与储能系统中。锂离子电池因具有自放电系数较低，使用寿命较长、充放电倍率大、工作温度范围大、能量密度大等特点受到研究人员重视[1]。

锂离子电池的SOC是反映锂离子电池剩余容量的指标。实现对SOC的精确估计不仅可以实时监视电池的电量状态，同时也可以避免电池过充过放，延长电池使用寿命[2-3]。由于传统的电流积分法与开路电压法已不能满足SOC估计精度与鲁棒性的要求，目前，广泛应用SOC的估计方法可以分为基于等效模型的方法与数值驱动的人工智能算法的方法[4]。数值驱动的方法将电池视作黑箱模型，利用大量数据进行训练得出SOC结果，其具有代表性的方法有支持向量机法(SVM)、神经网络法及其改进形式等[5-7]。基于等效模型的估计方法使用一系列数学表达式反映电池的充放电与其他的化学特性，应用较多就是利用滤波算法结合等效模型的方法[8-9]。如非线性卡尔曼滤波法、粒子滤波法等。为了提升估计性能，有学者加入平方根算法、自适应算法，其改进后的非线性卡尔曼滤波显著提升了SOC的估计性能[10-11]。

针对SOC的精确估计问题，利用嵌入式容积准则改进传统容积卡尔曼滤波(CKF)，通过加入强跟踪滤波以提升算法的噪声自适应能力，在进一步增加估计精度的同时提升算法的鲁棒性，引入奇异值分解解决由于环境噪声协方差矩阵初值非严格正定导致的算法无法正常运行的问题，通过电池在特定工况下的对比仿真验证其有效性。

1 锂电池模型建立与参数辨识

1.1 锂电池模型

锂电池内部化学反应不便于直接用于工程中，二阶等效模型考虑了电池内部工作过程，以两对电阻电容网络分别反映电池的电化学极化与浓度极化。该模型不仅满足反映电池主要特性的要求，计算复杂程度也相对较低[12]。锂电池的二阶等效模型电路如图1所示。其中，Uoc是一个理想电压源，代表电池的开路电压；It代表电池的终端电流；R0表现电池的阻性；R1、C1与R2、C2反映电池的极化特性，其电压分别为U1、U2；Ut代表模型的端电压。

图1 二阶等效模型Fig. 1 2-order equivalent model

根据基尔霍夫电路定律，二阶等效模型电路方程

(1)

SOC定义为现有容量与额定容量的比值，工程上应用的计算方式为

(2)

式中：ηSOC0——ηSOC的初值，额定容量时为1；

η——库伦效率；

Qc——电池的额定容量，Ah；

i——电池电流，A。

依据式(1)、(2)可知，二阶等效模型的电池状态方程为

(3)

式中：τ1、τ2——时间常数，为电阻电容乘积；

wk——系统噪声协方差；

It k——某一时刻输出电流；

vk——测量噪声协方差。

1.2 辨识参数方程的求解

模型建立完毕后，需要利用在线参数辨识识别等效模型的各项参数。在线参数辨识基于最小二乘法或其改进形式来对电池模型中的参数进行递推计算。其可以避免离线参数辨识的计算误差和因电池处于不同工况导致的辨识结果不同的情况出现[13-14]。由式(3)可得，最小二乘标准形式为

Ut k-Uoc k=a1(Uoc k-1-Ut k-1)+a2(Uoc k-2-

Ut k-2)+a3Ik+a4Ik-1+a5Ik-2,

(4)

式中：a1～a5——包含τ1、τ2、R0、R1、R2的系数；

Ik——电流离散形式。

式(4)即可用于最小二乘法进行辨识。

1.3 最小二乘法辨识

递推最小二乘法是一种通过最小化误差平方和原则来估计系统中的未知参数。对照式(4)，设Ut k-Uoc k为Hk，得出系统的最小二乘方程为

Hk=Φkθk+ψk,

(5)

式中：H——输出状态;

θ——辨识参数矩阵，θ=[-a1,a2,a3,a4,a5]T;

Φ——输出矩阵，Φ=[Hk-1,Hk-2,Ik,Ik-1,Ik-2];

ψ——系统噪声。

对照式(4)、(5)，对应的最小二乘法的迭代方程为

式中：P——误差协方差矩阵；

G——最小二乘增益；

λ——遗忘因子，一般取0.995；

I——单位矩阵。

为了验证模型的具体精度，采用平均绝对误差e与均方根误差σ衡量，定义为

(6)

式中：ε——估计值与真实值的差值；

N——差值个数。

2 改进容积卡尔曼滤波

CKF因其滤波效果好，可扩展性强，相比其他非线性卡尔曼滤波算法用时较少等优点而受到广泛应用[15]。但随着对电池SOC估计精度与鲁棒性需求日益提高，传统CKF逐渐不能满足这一要求。

2.1 嵌入式容积准则

传统CKF采用三阶球面-镜像容积准则，在该准则下，CKF在非线性方程的近似积分中选取的一系列容积点的权值为常数，这可能导致如选取系统中容积点超过积分区域导致无法定义或引起计算困难等情况出现[16-17]。

有学者依据传统CKF的缺陷，以Genz等[18]推导出的基于在固定积分区间上对称的积分方程(嵌入式积分法则)为基础，推导出经嵌入式容积准则改进的嵌入式容积卡尔曼滤波(ECKF)。

基于嵌入式容积准则，针对一个n维在整个实数域的无穷区间积分函数为

式中，w——积分自变量的权值。

为了实现对G(f)进行逼近，就需要构建一个对称的集合L，转化积分为

式中：A——降序排列的集合；

a——A的元素;

w0、w——积分轨迹上相对应i与δ的权值。

ECKF的优势在于利用嵌入式积分法则将n阶系统容积点个数从2n个变成2n+1个，同时，改变了容积点相应的权值，使其不再是常数。相比于五阶或更高阶的CKF，ECKF运行时间更短，多数情况可以达到近似五阶CKF精度[19]。由式(3)可知，系统为3阶，则容积点为9个，嵌入式容积准则下ECKF的容积点与对应权值的求取规则为

式中：δ——3×9阶矩阵，第一列为0，其余列为±1；

μ——嵌入式族参数，一般取1。

为了保证迭代过程中算法的数值稳定性，加入平方根算法得出SRECKF。平方根算法可以使其协方差在迭代过程中以平方根的形式传递，避免CKF中Cholesky分解错误导致算法出错，增加算法运行可靠性[20]。SRECKF迭代过程如下。

将式(3)视作一个状态变量为x，输出变量为z非线性系统，其方程为

式中：f、h——非线性函数；

u——输入变量。

利用前一时刻状态量xk-1与给定的误差协方差求解其平方根S1、容积点xi与状态先验估计值j为

(7)

式中：P——状态变量协方差矩阵；

wi——容积点对应权值。

计算状态过程变量χ1与矩阵[χ1 k-1,SQ k-1]的平方根S2为

式中：SQ——系统噪声协方差矩阵Q平方根；

qr——对当前矩阵进行正交三角分解。

计算新容积点Xi为

Xi k-1=S2 k-1ζi+jk-1，i=1,2,…,9。

将容积点Xi代入观测方程得出观测先验估计值zi，并求解观测预测值l与观测过程变量为

利用矩阵[Zk-1,SR k-1]可求出观测自协方差平方根矩阵Szz为

Szz k-1=qr([Zk-1,SR k-1])，

(8)

式中，SR——观测噪声协方差矩阵R的平方根；

新过程变量χ2与互协方差矩阵Pxz为

(9)

计算SRECKF的卡尔曼滤波增益Wk为

计算状态变量的后验估计值与平方根的后验估计值，并在之后不需要再对P矩阵进行平方根求解，直接更新平方根值为

至此，完成了一次算法迭代。

2.2 强跟踪滤波

强跟踪滤波一种优化滤波过程的一种算法，其利用渐消因子对历史数据权重进行弱化，调节滤波的增益，使其在每个时刻的观测值残差保持正交，进而滤波精度与增强滤波算法鲁棒性[21]。

计算观测估计量的残差为

εk=zk-lk。

(10)

计算描述观测变量残差序列为

(11)

式中：ρ——遗忘因子，一般取0.9；

ε——观测真实值与l的残差。

求解强跟踪渐消因子λ的求解过程为

(12)

式中：N、M——过程变量矩阵；

β——弱化因子，一般取0.98；

λ——自适应渐消因子；

tr——求当前矩阵的迹。

自协方差平方根矩阵、观测误差协方差矩阵与互协方差矩阵为

(13)

将式(8)、(9)替换为式(10)～(13)即可将强跟踪滤波与SRECKF结合。

2.3 奇异值分解

噪声的协方差矩阵恒为正定或半正定，但Cholesky分解必须保证待分解矩阵保持严格正定。平方根算法可以保证在迭代过程中噪声协方差矩阵保证严格正定，但如式(7)所示，噪声协方差矩阵初值的Cholesky分解不在平方根算法的优化范围内，因此仍有因初值矩阵半正定导致算法无法运行的可能[22]。

将所有Cholesky分解替换成奇异值分解可以解决矩阵半正定问题。以m×n阶矩阵P为例，替换奇异值分解的过程为

式中：U、V——m阶与n阶的酉矩阵；

S——P的奇异值组成的对角矩阵。

3 仿真与结果分析

仿真选用单体2.2 Ah的磷酸铁锂电池在35 ℃环境下的工况测试数据。针对模型参数辨识，使用动态应力工况(DST)下的测试数据。将辨识参数代入模型中与输出电压的对比如图2～4所示。

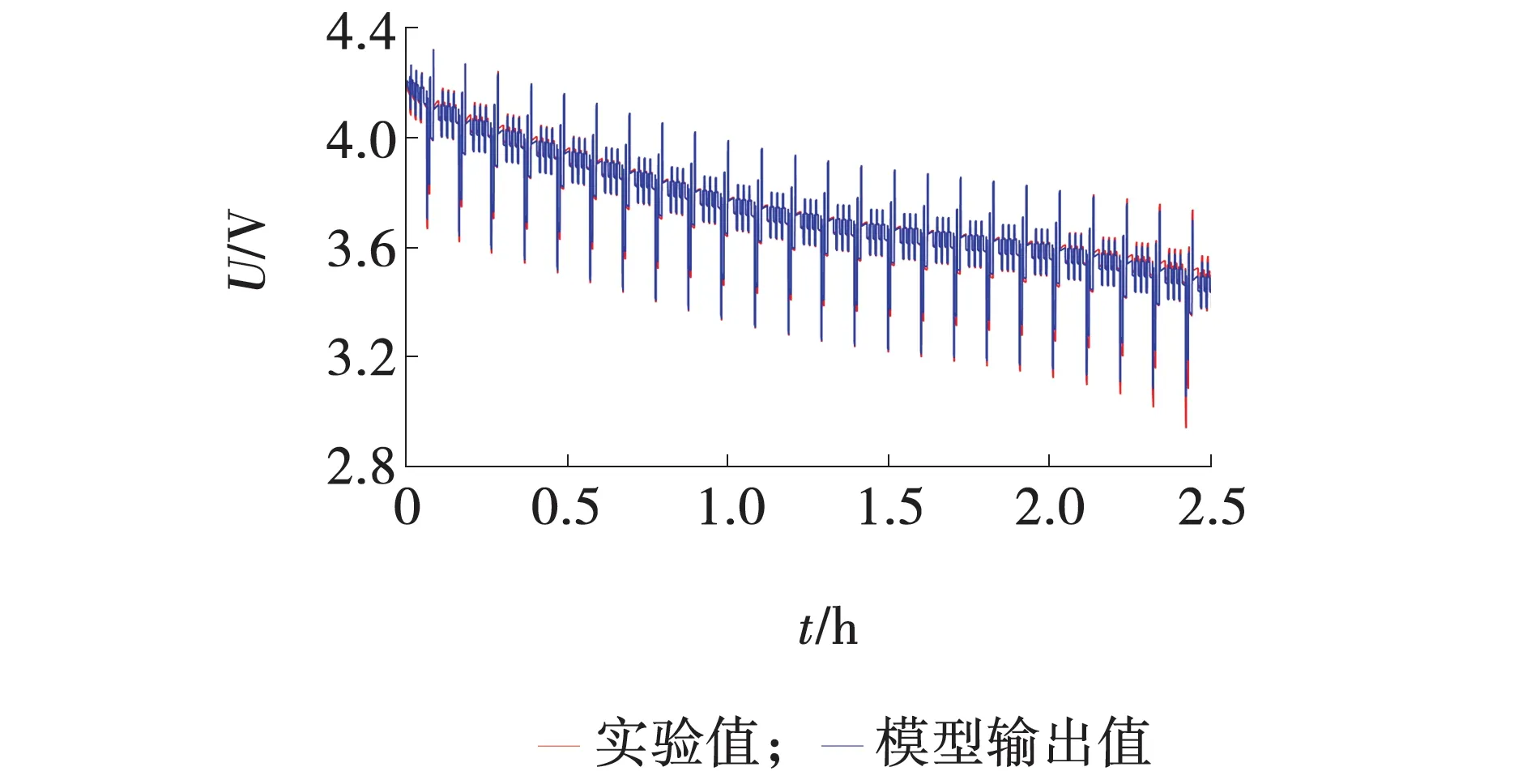
图2 电压对比结果Fig. 2 Comparison results of voltage

图3 电压对比结果局部放大Fig. 3 Local amplification of comparison results voltage

图4 电压绝对误差Fig. 4 Absolute error of voltage

从结果看出等效模型输出值与实验值契合度较高。模型输出电压值的平均绝对误差0.030，均方根误差0.037，均在3%左右，总体满足对SOC估计提供精确电池模型的需求。

SOC估计选用电池的直流脉冲工况，比较SRCKF、SRECKF与ISRECKF三种方法在输出电压加入随机噪声的环境下比较估计性能。随机噪声下输出电压如图5所示。

根据图6～8，三种算法均可以比较准确的在不定噪声环境下估计SOC，经过嵌入式容积准则优化的SRECKF估计效果要优于SRCKF，这是因为容积点的增多与权值分布的优化使算法的精度提高。而经过强跟踪滤波优化的ISRECKF要进一步优于SRECKF，这表明了强跟踪滤波通过利用渐消因子修正历史数据，显示出其自适应性，与卡尔曼滤波体系有着较好的结合效果。

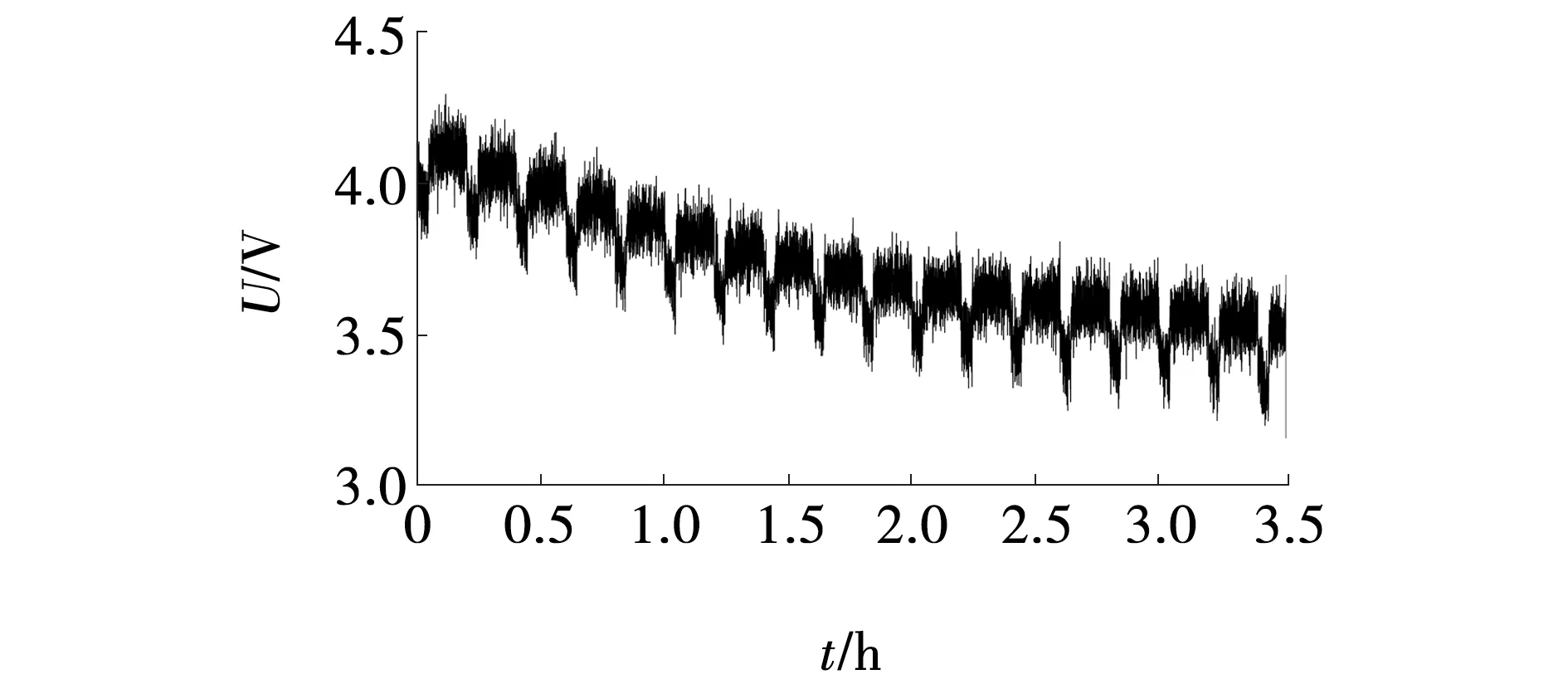
图5 在随机噪声下的端电压值Fig. 5 Terminal voltage under random noise

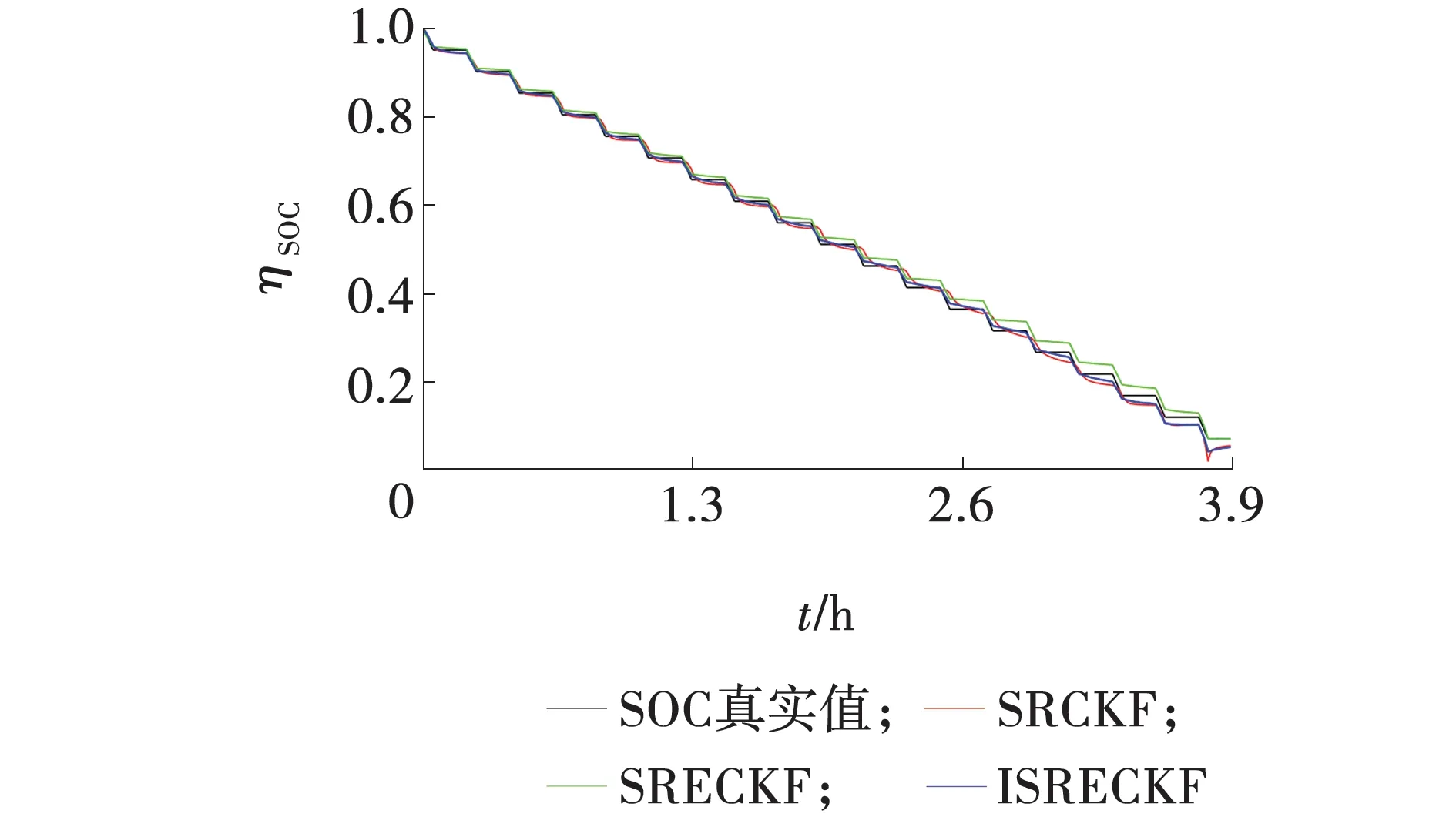
图6 SOC估计结果Fig. 6 SOC estimation results

图7 SOC估计结果局部放大Fig. 7 Local amplification of SOC estimation results

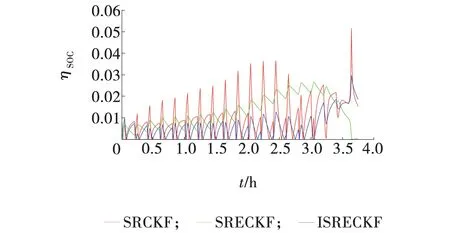
图8 SOC估计绝对误差Fig. 8 SOC estimate absolute error

根据式(9)可得，计算三种方法的平均绝对误差与均方根误差，结果如表1所示。

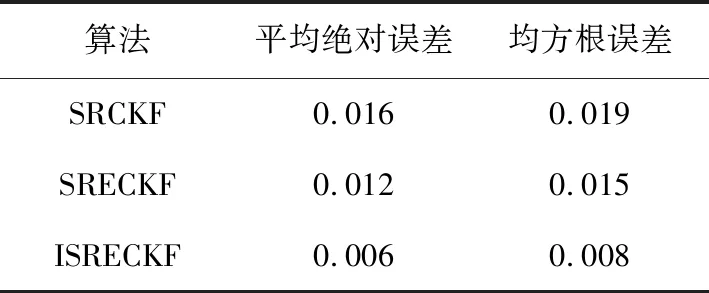
表1 SOC估计结果

算法的鲁棒性也是重要考查因素之一，鲁棒性决定了当系统设定SOC初值出现偏差后算法是否可以快速收敛并继续进行正常估计。为了验证算法的鲁棒性，设定SOC初值为0.8(20%初值偏差)，其估计结果如图9～11所示。

从图9～11可以看出，初值0.8情况下三种算法均未出现不收敛的情况，ISRECKF的估计效果依旧在三种算法中表现最好。从图11可以看出，ISRECKF的收敛时间最短，这是因为强跟踪滤波不仅可以提升算法对噪声的自适应性，同时也可以提升算法整体的鲁棒性。

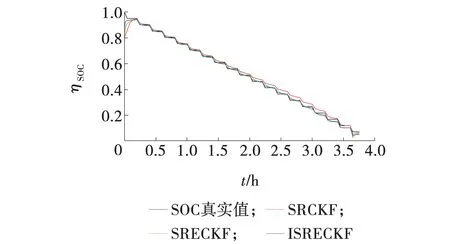
图9 初值0.8的SOC估计结果Fig. 9 SOC estimation results with the initial value 0.8

图10 初值0.8的SOC估计绝对误差Fig. 10 SOC estimate absolute error with initial value 0.8

图11 SOC初值0.8局部放大Fig. 11 Local magnification of initial value 0.8 of SOC

SOC初值0.8时三种方法的平均绝对误差、均方根误差与收敛时间结果如表2所示。

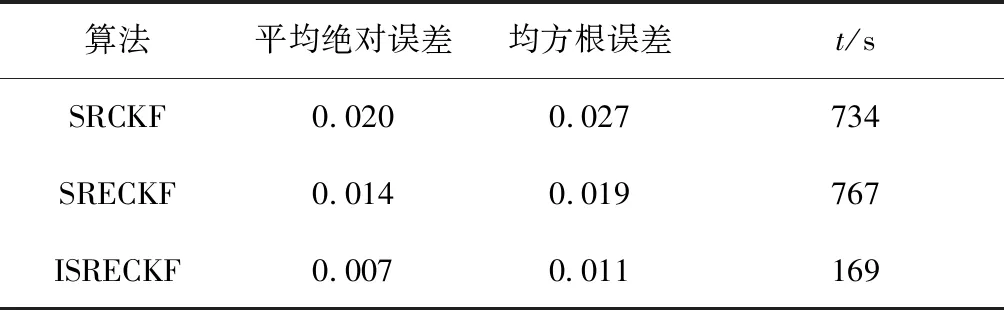
表2 SOC初值0.8估计结果

综合SOC初值为1与SOC初值为0.8两种情况的仿真结果，经过强跟踪滤波优化的ISRECKF综合性能最好，体现了所提出方法的优势。

4 结 论

(1)依照嵌入式容积准则改进了传统CKF，增加了CKF容积点，改进了权值分布，提升了算法的估计精度。又加入了强跟踪滤波，得出ISRECKF，在算法的精度进一步提升的同时增强了鲁棒性。

(2)通过电池的直流脉冲工况数据，在Matlab上进行仿真分析。结果表明对比SRCKF与SRECKF，ISRECKF具有最高的精度，最好的鲁棒性。初值没有偏差的情况下平均绝对误差为0.006，均方根误差为0.008；而在初值偏差20%的情况下平均绝对误差达到0.007、均方根误差达到0.011，收敛时间为169 s，实现了对锂离子电池SOC的精确估计。在后续工作中，将继续针对锂离子电池模型、CKF的基础理论进行改进，在进一步提升估计效果的同时尽量减少算法的执行时间，使其具有更好的实时性。