小学数学教学中明辨性思维的培养途径

丁大秋

（江苏省邳州市明德实验小学）

明辨性思维又称思辨性思维，它是培养学生创造性思维的前提和基础。明辨性思维既属于认知思维能力，又是一种认知思维过程。学生具有怀疑、明辨和反思的精神是数学明辨性思维的重要特质，是学生思维创新的核心。数学教学培养学生明辨性思维，需要在日常教学中结合数学学科特点有效渗透。具体可以从四个方面进行。

一、悦心、创境：筑起明辨性思维之“桥”

学生在心理上感到“自由”和“安全”是开展明辨性思维的前提。教师在教学中既要营造舒适的“心理场”，又要营造丰富的“情境场”，引导学生开展个性化的学习，为学生乐于动脑、勤于思考、积极探究“筑桥”。

（一）悦造“心理场”

教师在上课时，应该微笑着面对全体学生，在学生回答问题时，可以用赞许的目光、赏识的表情看着学生，耐心倾听，不轻易打断学生。当学生到黑板前板演或回答问题后，可以说一句：谢谢你。课堂上经常有欢声笑语和掌声，在这样的环境中，学生无比自豪和幸福，身心放松，思维活跃，能全身心地投入到学习中，自由大胆地参与讨论、辩驳等活动。

（二）创设“情境场”

数学情境是沟通生活世界与数学世界的桥梁，是明辨性思维得以顺利开展的重要载体。教师应积极构建在相对真实的数学教学情境中学习的认知路径，激发兴趣，丰富感知，引发想象，启迪探究。

在教学“分数的初步认识（二）”时，可以这样创设情境：猴妈妈把一个桃子平均分给它的两个猴宝宝，每只猴宝宝分到这个桃子的几分之几？猴妈妈看猴宝宝很快吃完了，又端来一盘桃子（6 个），每只猴宝宝又可以吃到几分之几呢？请学生用圆片代替桃子分一分。假如这盘桃子是4 个、8 个呢？再请学生试着用圆片分一分。观察图1 中三次分桃子的过程并思考：三盘桃子的个数都不一样，表示其中1 份的个数也不一样，为什么都可以用来表示呢？（如图1）

图1

理想的课堂应该是师生平等、彼此尊重、相互信任的，应该是学生生活甚至生命中的重要组成部分。教师应成为学生的良师，更应成为学生的益友，应该让每一堂课都成为与学生心灵对话的舞台，要重视“情境场”的创设，让“情境场”成为学生的“探究场”，吸引学生主动学习。

二、自信、好奇：铺就明辨性思维之“路”

明辨性思维也是一种内隐的思维品质。教学中，教师应该帮助学生树立自信心，激发好奇心，为明辨性思维的培养“铺路”。

（一）自信为明辨提供了可能

当学生在学习上遇到困难和挫折时，教师应鼓励和鞭策。当发现学生身上闪光点时，应及时地给予表扬，增强学生的自信心，让学生树立“我行，我一定行”的信念。在课堂上，当学生回答问题磕磕巴巴、吞吞吐吐时，教师可以说：“别急，老师相信你一定会有精彩的回答”；当学生站起来，却不知说些什么时，教师可以说：“再认真地想一想，老师等着你，好吗？”学生回答完问题，不管对错，都应该让学生体面地、不带着遗憾地坐下。

（二）好奇为明辨提供了动力

好奇是知识的萌芽，是学生开展探究活动的原动力。好奇心强的学生在学习上往往精力充沛，对周围的事物有着浓厚的兴趣，遇到问题喜欢刨根问底，在他们的脑海中充满了想象。

在教学“3 的倍数特征”时，课始，我说：“老师有一个‘听音辨数’的特异功能，只要听到你们在计数器上拨珠子的声音就知道拨出来的数是不是3 的倍数。”而后，请一名学生当操作员，到讲台前拨数，让台下的学生用计算器验证。我的准确判断，迎来学生的阵阵喝彩。

“听音辨数”极大地激发了学生的好奇心，学生急于想知道我的这个本领是怎样练成的，自然也就带着浓厚的兴趣投入到了新课的学习之中。随着探究的逐步深入，学生豁然开朗，原来我这个特异本领，就是应用了3 的倍数特征，他们发现数学结论的自豪感也应然而生。

“好学生是夸出来的。”教师应以宽广博大的胸怀赏识学生，对学生进行积极地心理暗示。教师应该是学生学习遇到困难时的有力支持者，学生学习行为的促进者。作为教师，在教学中应不断创造条件，让学生产生好奇心，应引导学生多观察和留意身边的事物，呵护奇思妙想，允许异想天开，引燃求知热情。

三、质疑、反思：翻越明辨性思维之“山”

明辨性思维能力是学生必备的基本思维能力之一。教师在日常教学中应有效渗透明辨性思维，用开放的、明辨的视野审视自身的教学，让学生通过质疑和反思，成功翻越明辨性思维之“山”。

（一）从质疑中学会明辨思维

质疑作为一种能力和素养，孕育着创新，是思维的开端。主动质疑则是学生拥有明辨性思维的开端。质疑精神和质疑能力是人们应有的素养，教师在教学中应该高度关注。

在探究“3的倍数特征”时，有学生提问：“为什么2 和5 的倍数特征看个位，3 的倍数特征要看各个数位上的数字之和呢？”面对这样的质疑，我适时地提出了表扬，并请学生分小棒研究132，看看有什么发现。学生发现：100 根小棒，3 个一份来分，能分掉3的最大倍数99 根，还剩1 个，30 根小棒可以看成3捆，3 个一份来分，每捆能分掉3 的最大倍数9 根，剩1个，3捆剩3个。这样，各部分剩下的根数正好是各个数位上的数，把剩下的小棒合起来继续分，恰好可以分完。我再请学生列举其他的数，用小棒分一分，学生发现每次分完剩下的小棒根数正好是各部分剩下的数。学生终于明白，原来各个数位上的数加起来，就是把每次分剩下的数加起来继续分，如果加起来的数是3的倍数，原来的数一定是3的倍数。

很多教师都按照“圈数、观察、猜想、举例验证、归纳概括”这一思路展开教学，如此教学，符合教材的编写意图，学生只要发现了3 的倍数特征，目标就达成了。但是在上述教学中，学生受到2和5的倍数特征的影响，产生了“为什么3 的倍数特征不看个位上的数”的疑问。我抓住学生的疑问，让他们通过摆小棒一探究竟，使他们终于明白了其中的道理，这才是真正意义上的数学探索之旅。学生的学习应是不断向未知挺进的旅程，只有让学生多问几个“为什么”，他们才有可能在更多的未知领域里尽情地遨游和探索。作为教师，应培养学生质疑问难的能力，引导他们发现问题、研究问题、解决问题、产生新问题、探索新问题，解决新问题。如此循环往复，必将推动学生在求知的道路上向更高的层次迈进。

（二）从反思中增强明辨意识

教师在教学中应该促使学生自觉地对学习过程与方法、目标达成、情感态度等方面进行比较、总结和反思，使其学会自我评估，增强明辨意识。

在教学“球的反弹高度”时，学生通过观察三种球的反弹现象，提出问题：球的反弹高度与下落的高度有着怎样的关系？不同的球反弹的情况是否相同？随后，通过多次实验，收集数据，发现了数学结论。最后，我引导学生回顾反思：通过本次活动，你有什么体会？学生通过独立思考、小组明辨、全班交流认为，认真做实验，才能采集到可靠的数据；结论的得出应源于对数据的分析，数据越充分，越容易发现规律。

上述教学活动，当学生发现了球的反弹规律之后，我没有按时地让学生结束学习活动，而是组织学生通过思考、讨论和交流，体会解决生活中的实际问题、开展实验的必要性，体会收集数据的重要性。在教材中，“探索规律”“解决问题策略”之类的课程都安排了类似的学习活动，这一活动的开展，绝不是走过场，而是有针对性地引导学生认真梳理探究过程，有条理地表达内心的思考，有效增强反思的意识。

质疑给学生的明辨性思维发展插上了腾飞的“翅膀”，可以使学生的明辨性思维的“羽翼”更加丰满。“有疑则进，无疑则退”。教学中，要让学生有大“疑”，学生才能有大“进”。反思有利于结构化的学习，有利于学生对学习方法、活动经验的深刻反省，有利于学生主动建构知识，有利于学生的思维向更深处漫溯。

四、阅读、纠错：涉过明辨性思维之“水”

数学阅读在发展学生数学思考、提高数学理解力、提升数学思维方面具有重要作用。学生明辨性思维的本质是学习的认知过程，衡量认知过程的优劣，不是看做题正确与否，而是看纠错的“速率”快慢。为此，教师应该让学生以“前所未有的速度”涉过明辨性思维之“水”，得到实实在在地发展。

（一）从阅读中明辨已有结论

数学阅读不是走马观花，更不是记忆数学结论，而是包含了质疑明辨的精神。数学的明辨性阅读包括对教材的怀疑、探究和否定创新三个层次。在教学中提倡学生对教材进行明辨，对数学结论不是全盘接受，而是不断地怀疑，提出和教材、专家不同的观点。

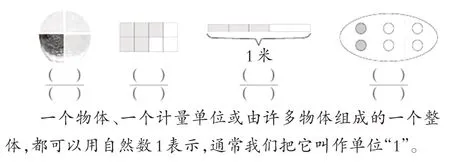
图2

一名学生阅读图2 之后认为，应该在“一个物体”之后加上“一个图形”才更准确。我及时组织全班学生辨析，很大一部分学生赞同这位学生的观点，理由是：在认识面积时，把物体表面的大小叫作物体表面的面积，把平面图形的大小叫作平面图形的面积，可见物体和图形是不同的概念。但也有一部分学生认为，如果这个长方形代表的是一个花园或者一个池塘就可以看成一个物体。

能对教材的编写提出自己的看法，是我长期开展明辨性思维训练的结果。学生不仅指出了教材编写上的“漏洞”，而且给出了他们的理由，更有一部分学生提出用长方形可以代表物体的看法。此时，加不加“一个图形”这四个字就显得并不重要了，重要的是学生对单位“1”的理解越来越深刻，有效突破了教学难点。这样，看似节外生枝，实则精彩纷呈。

（二）从纠错中明辨错因

学生的错误是宝贵的资源，学生无需紧张、自责、回避，教师无需生气、批评、责怪。教师应善待学生出现的错误，帮助学生找出错因，教给学生改正的方法，引领学生修正错误。习得明辨性思维不是让学生不犯错，关键是能及时地纠错，养成对错因进行分析的良好习惯。

在教学“用字母表示数”时，我让学生编儿歌：（ ）青蛙（ ）张嘴（ ）只眼睛（ ）条腿。学生由1 只青蛙1 张嘴、2 只眼睛4 条腿开始拍手唱，当唱到 7 只青蛙 7 张嘴、14 只眼睛 28 条腿的时候，唱不下去了，他们感觉太麻烦。我请学生想办法用字母表示为的知识表示出这首儿歌，学生出现了两种错误答案：①x只青蛙x张嘴x只眼睛x条腿，②a只青蛙b张嘴c只眼睛d条腿。我把这两种错误的答案和正确的答案一起投影在大屏幕上，请学生辨析。学生经过争辩认为，答案①中如果x=1，就会出现1只青蛙1张嘴、1只眼睛1条腿的怪现象，所以不能用同一个字母来表示这四个不同的未知量；答案②虽然用不同的字母表示不同的量，但看不清这四个数量之间的关系，所以也是错误的。

学生出现错误在所难免。上述教学中，我适时抓住错误资源，组织学生辨析，让“学生真正地站在了课的中央”。学生在争辩过程中，进一步理解了用字母表示数的简洁性和概括性，懂得了字母表示数不仅仅表示结果，更重要的是表示数量之间的关系（数学要研究数量关系）。学生的错误是教学中的宝贵资源，面对学生的错误，教师应因势利导，把判决权留给学生。

其实，学生在平时的数学练习中，也会或多或少地做错题。可以让学生利用纠错本，从错误解法、错因分析、正确解法、错误启示等四个方面来整理错题，这样以后做题时就会少出错甚至不出错。

学生对教材发起挑战，不迷信权威，“不唯书至上”，培养了追求真理，求真向善的良好品质，理解了“理越辩越明”的道理。数学学习过程是不断出错、纠错的过程，学生在错因分析和错误启示中，找到了学习的诀窍，错题不断被纠正，学生不断进步，循环往复，学习经验也会提升。

总之，明辨性思维让学生的思维更深刻、更发散、更有创造性。明辨性思维的培养应该融合在平时的教育教学之中。教师需要以开放的视野展开教学，要带领学生“筑桥铺路，跋山涉水”，大胆实践，不断创新，超越自我。