基于线性判别分析分离印章与签名字迹的研究＊

韩虹 孙鹏 王运宏 单大国

1. 中国刑事警察学院 2. 司法部司法鉴定重点实验室

引言

签名字迹是最常用的身份认证方法，确认签名的真实性对于防止诈骗、检验文件真伪、身份检查有着十分重要的作用。大多数民事案件中，委托签名字迹检验鉴定的对象大部分为印章与签名相重叠的文件，此时需要把印章与签名分离开，以便于后续的印章真伪鉴定和签名字迹的同一鉴定[1]。但当签名笔迹与其他物质相结合时，字迹常出现的细节特征会因为与其他颜色的叠加被掩盖，从而影响特征的正常观察，导致鉴定人员忽略相关特征，最终对鉴定结果判定产生一定的影响。因此，将印章与签名笔迹进行有效分离，同时尽可能的保留笔迹的细节特征是笔迹鉴定工作重要的一部分。

印章与签名笔迹的分离实质上是关于图像分割的问题，面对此类问题，通常采用阈值法来达到图像分割的目的[2]。目前基于图像处理的印章与签名字迹分割法主要为阈值处理，最早的阈值处理法是由Prewitt等人[3]提出的谷底最小值法，该方法将直方图中的局部极小值作为阈值对图像进行分割，但经过实验后发现，该方法并不适合直方图中双峰间距离宽广的图像，同时对于单峰图像也不适用。Ridler[4]等人虽然对该方法进行了改进，采用迭代的方式来确定局部极小值，但其阈值确定的原理和谷底最小值法相同，且处理结果的表现同样受到待处理图像直方图质量的限制。而后Kapur等人[5]提出了一维最大熵方法，引入熵概念，将图像的灰度级概率分布分为两类，求得每一种分布的熵并对其进行求和，选择合适的阈值最大化两者之和，以获得物体和图片背景分布之间的最大信息，从而实现物体与背景之间的分割。

目前使用的阈值分割方法都是直接利用图像的灰度直方图信息进行阈值确定，忽略了色彩空间中印章与签名字迹两类数据之间的关系，导致阈值处理后少量签名笔迹数据被错误划分，从而出现印章与笔迹无法完全分离或笔迹细节特征丢失的现象，最终影响签名字迹的比对。针对上述问题，本文提出在进行阈值处理之前，先对印章和书写字迹的数据进行分类，而不是直接对图像灰度级进行分类，然后再结合直方图信息，选择合适的阈值实现两者之间的分割。该方法的具体流程如图1所示。

一、基于线性判别分析分离法的实现

线性判别分析是一种有监督学习的降维技术，在人脸检测、人脸识别、目标跟踪和检测中得以广泛应用，因为在进行模式识别过程中总是面临着数据维数过高的问题，这些高维特征是具有相关性的或是冗余的，往往可以嵌入某个低维空间中，所以对数据进行降维是进行图像处理过程中的一个重要步骤[6]。由于本文讨论的问题仅限于印章和签名字迹的两类数据，所以暂时不需要考虑对数据进行降维，而只需要解决二分类的问题。因此，选择使用Fisher线性判别分析来实现。

（一）颜色分量的选择

一张图片中，有的颜色分量之间会呈现出线性相关性，而有的颜色分量之间能够呈现出线性可分性[7]。对线性相关性太强的数据进行Fisher线性判别很难将两者进行分离，经过最终的阈值处理后仍然会呈现出数据被错误划分的现象。因此，对两类数据进行分类之前需要先确定适合印章数据和签名字迹数据分离的颜色分量，减少两类数据被错误划分的情况，达到印章和笔迹在完全分离的情况下又保留笔迹原有细节特征的要求。

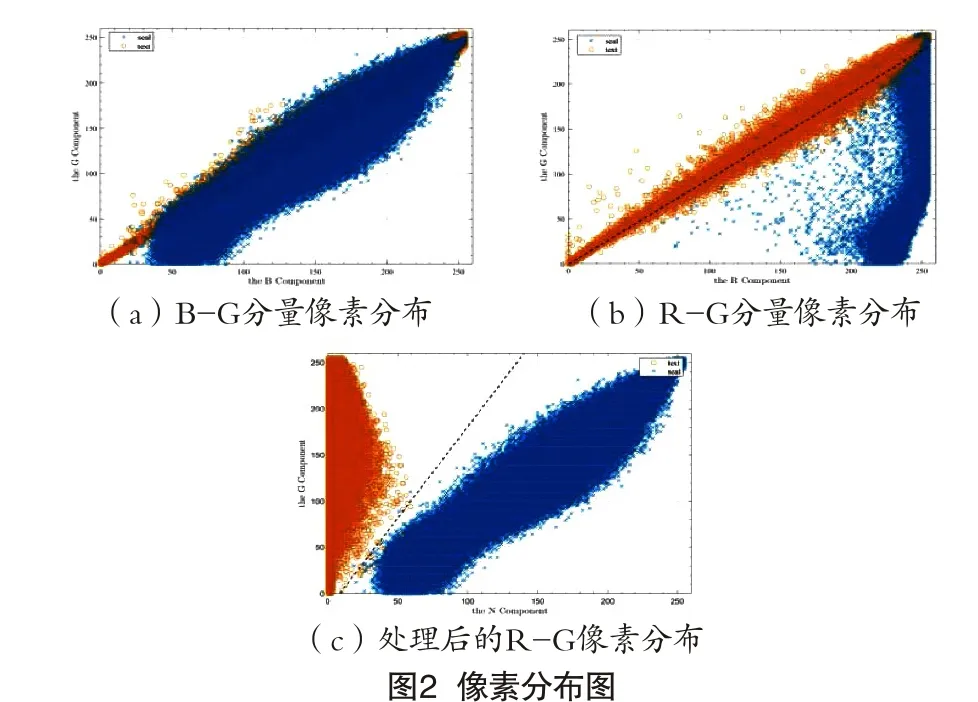
图2（a）显示了待处理图片的像素分布情况，可以看到，印章数据与签名数据的B分量和G分量存在大部分重叠的现象，两者具有明显的线性相关性[8]，观察图2（b）发现，R和G分量的像素分布只存在少部分重叠，Fisher线性判别分析可行性高，又因为B分量和G分量具有高度的线性相关性，故选择对R分量和G分量进行数据分离。

（二）线性判别分析与阈值处理

Fisher线性判别分析通过公式（1）将数据投影到直线上，其中ω 为对两类数据进行分离的最佳投影向量，为实现印章与签名字迹的分离，就需要使这两类数据经过投影后形成的新的投影点尽可能的远，即印章数据中心 与签名字迹数据中心 的距离最大化，而两类数据内部的各投影点距离要保持尽可能的近。因此，引入类间散度矩阵 和类内散度矩阵Sm，通过公式（2）最大化两者的广义瑞利商，使得投影后印章数据与签名字迹数据的类间散度矩阵最大且类内散度矩阵最小。最终计算得到向量ω，如公式（3）所示：

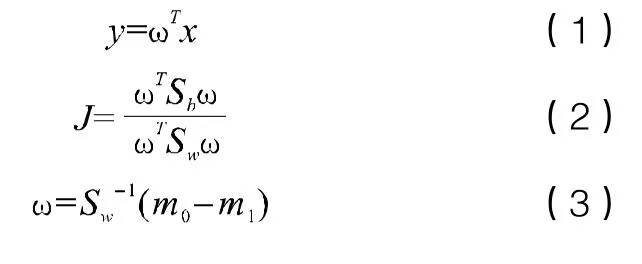
图2（c）是R分量和G分量经过线性判别分析后的像素分布图，与图2（b）进行对比，可以明显看出两类数据已被很好的分离开。在完成以上工作之后，只需要通过图像直方图信息确定其阈值就可以完成印章和签名字迹分割的整个任务。

二、实验准备与结果分析

（一）实验准备

本文实验所用扫描仪为佳能MG2580S，文件扫描格式为PDF；所用的计算机配置为Windows 10操作系统，CPU类型为第六代智能英特尔酷睿i5四核处理器，图像处理编程环境为Matlab。

为保证实验的多样性和可靠性，实验数据集按以下方法制作：首先在白纸上分别写下“实验签名”、“实验用字”、“笔记检验”等字，将其分为A、B、C三组，每组24个样本，对每个样本进行编号后进行扫描，作为真值图像与实验结果进行比对。使用同一枚印章在制作好的笔迹样本上进行盖印，确保印文与字迹有较多重叠，对盖印后的图片进行扫描作为样本，最终得到的印章签名样本图像共144幅（72幅真值图，72幅样本），每幅图像的大小为1800×1800。

由于本文最终是根据直方图信息确定阈值，为了说明本方法在分离图像和细节保留方面的有效性，选择同样基于直方图的较为经典的谷底最小值法和一维最大熵法对样本进行处理，将其结果与基于线性判别分析方法进行比对。同时，引入矩阵相关系数和特征相似度（Feature Similarity，FSIM）对结果进行客观测评，将评价数值绘制成折线图，更加直观的展示三种方法之间的优劣，并在最后通过对评价指标结果均值的分析证明该方法的有效性。

（二）实验结果与分析

整个实验遵循控制变量原则，在相同实验环境下，分别使用一维最大熵法、谷底最小值法以及本文提出的基于线性判别分析的方法对原始图像进行处理，从三组实验结果中各

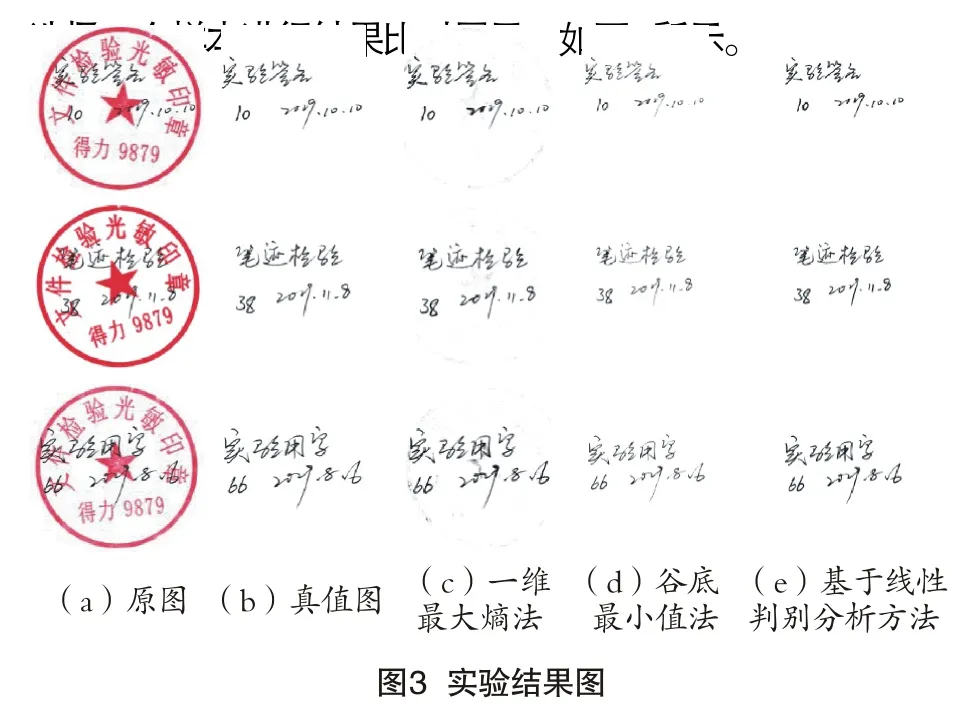
观察图3（c）列发现，利用一维最大熵法进行实验后得到的签名字迹在笔画粗细方面基本没有变化，但其与印章未能实现完全分离。图3（d）列的结果说明，虽然使用谷底最小值法能够将两者分离，签名字迹却出现了笔画变细以及伪漏白现象，这两种情况对于笔迹鉴定的真实性会产生严重干扰。通过图3（e）列可以观察到，使用本文方法得到的签名字迹，印章与字迹不仅能完全分离，而且分离后笔画变细和伪漏白现象均得到了很好的解决。

为客观评估提取效果，使用矩阵相关系数和FSIM对签名字迹提取效果进行评价，并记录其测评数据值：

1. 矩阵相关系数

计算提取的印章签名与真值签名的相关系数，用于度量其线性相关性。其数学表达式为：

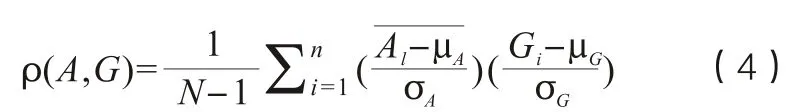
2. 特征相似度

FSIM通过计算提取签名字迹的局部相位一致性及梯度幅值的相似度，得出加权匹配后的相似度分数，值越大说明当前签名字迹越接近真值签名字迹，其数学表达式为：

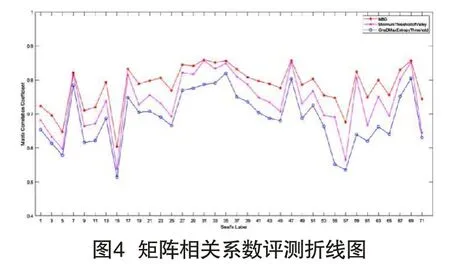
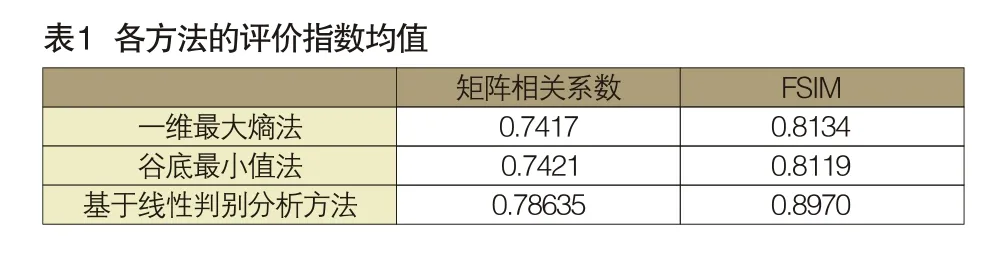
观察图4、图5发现，三种方法得到的评测值变化趋势基本一致，但利用本文方法得到的签名字迹的评估值始终高于另外两种方法，且波动更加平缓，由此可见其鲁棒性更高。三种方法的评价均值详见表1，该数据同样表明，本文方法相较于另外两种方法有一定程度的提高。其中，矩阵相关系数比一维最大熵法提高了6%，比谷底最小值法提高了5%；FSIM系数比一维最大熵法提高了10.2%，相对于谷底最小值法提高了10.5%。由此可见，本文提出的基于线性判别分析的印章与签名字迹分离方法的有效性和鲁棒性更高。

?

三、结论

本文提出了一种基于线性判别分析实现印章与签名字迹分离的方法，首先分析色彩分量之间的像素分布，找到适合分离的两个颜色分量，经过线性判别分析完成二分类后，通过图像直方图信息选择阈值进行处理。结果表明，该方法不仅能够实现印章与签名字迹的完全分离，还能够保持签名字迹的原有特征不被破坏，比直接通过直方图选取阈值以及直接对图像灰度级进行分类的效果更好。未来的工作将致力于印章与签名字迹重叠情况下提取印章的新方法。