基于粒子群支持向量机的损伤判定方法

冼旭东

(广西大学土木建筑工程学院 广西 南宁 530001)

引言

伴随信息技术的不断发展以及工程技术人员对结构损伤判定的不断深入研究，不同学科交互共同发展已成为大势所趋，在结构损伤判定这一领域引入其他学科的理论，同样能得到更多有利于解决问题的思路[1]。例如BP神经网络、遗传算法及小波分析就被广大学者用于对结构损伤的判定工作当中。支持向量机作为机器学习当中诸多算法的一种，它理论的成熟时间较晚，模式较为新颖，原理也相对简单易懂。近年来支持向量机的理论日渐完善，但将其用于结构损伤的实践较少，并且经验尚且不足[2]。本文通过建立桥梁结构的有限元模型并对桥梁损伤进行模拟，并利用支持向量机的分类功能实现对桥梁结构损伤位置进行判定。

一、支持向量分类机的基本原理

支持向量机是根据线性可分条件下最优超平面推出的，假定有n个样本，D=[(xi,yi)|i=1,2，…，n]，xi∈Rn，yi∈<-1,+1>能被某H：w·x+b超平面正确分开，即其他类型的样本不会出现在某一类型的样本当中，并且分类的距离达到最大化，而这一分类的平面就是最优超平面。

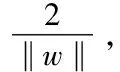
(1.1)

将两个约束条件合并可得：

yi[(w·xi)+b]-1≥0，i=1，2，…,n

(1.2)

利用(2.4)所构造出的分类超平面将全部样本进行没有错误的分类，这是机制向量机的根本目的。

(1.3)

s.t.yi[(w·xi)+b]-1≥0，i=1，2，…,n

此为凸二次问题，其解能通过拉格朗日函数求解获得，求解过程如下所示：

(1.4)

式中的αi≥0是拉格朗日乘子。

首先对w和b分别求偏导，并令他们为0有：

(1.5)

将式(2.6)带入式(2.5)可得：

(1.6)

(1.7)

如此便可获取拉格朗日函数对偶形式，这种对偶形式较有利于数值求解。这样一来构造最优超平面的问题就能转化成较为简单的对偶二次规划问题

(1.8)

(1.9)

b*为分类阀值，能根据约束条件求解，通过上述方程解得的最优分类面函数：

(1.10)

由式(2.13)中只是对支持向量求和，而不是支持向量所对应的α，均记作0，通过此判别式便能得出新输入的数据类别，此为SVM的最一般表述。

二、粒子群优化算法

(一)粒子群算法基本理论

假设n维空间中存在一个种群X={X1,X2,…,Xn}在执行相应的搜索工作，该种群由若干数量的粒子成，而各粒子所处的方位Xi={xi1,xi2,…,xin}均对应了一个问题里的解。种群中的各粒子在通过随机运动对自身位置xid进行改变的同时不断执行对新解的搜寻工作。同时，单个粒子也会根据其记忆功能将搜索过程中获取的最优解Pid储存起来，而获取当前种群最优解Pgd只需对各粒子搜索的最优接进行比对便可。群体中各粒子都有自身的搜索速度，记作V={vi1,vi2,…,vin}，当单个粒子的最优解与群体最优解均搜索完成后，各粒子的速度都会根据下式(2.1)、(2.2)更新。

vid(t+1)=ωvid(t)+η1rand()(pid-xid(t))+η1rand()(pgd-xgd(t))

(2.1)

xid(t+1)=xid(t)+vid(t+1)

(2.2)

在式中，vid(t+1)代表第i个粒子在t+1次的迭代里第d个维度上的速度，ω表示惯性权重，η1、η2表示加速常数，rand()表示0到1间随机的一个数。另外，粒子速度的上限记为vmax，当式中vid(t+1)>vmax的时候，vid(t+1)=vmax，同理在vid(t+1)<-vmax时，vid(t+1)=-vmax。

(二)粒子群优化支持向量机参数的预测方法

核函数σ与惩罚函数C以及不敏感损失参数ε的取值与支持向量机的计算精度都密切相关。使用粒子群优化算法将所需优化模型的参数进行全面且高效率的搜寻，进而使从而使得试算所造成的模糊定位得以降低，同时提升了模型的计算精度。首先对群体进行随机初始化，并由此得出由若干粒子构成的种群，随后将表示参数向量的各粒子选定成支持向量机中的计算参数，并对其做相应的迭代训练，最后记录下每一次迭代所获得的参数值，当迭代至满足要求后，所获取的粒子就是使得适应度函数最大的粒子，此粒子表示被SVM训练达到最优的参数，这就是基于PSO-SVM的参数优化算法，算法流程如下所示。

图1 PSO-SVM算法流程

三、粒子群优化支持向量机的损伤判定方法

(一)特征向量的构建

为确保本泛化性，本文选取结构中刚度折减为20%、40%、60%的曲率模态差作为利用支持向量机分类算法实现受损位置识别功能时的训练样本，与此同时，选取损伤程度为10%、30%、50%的特征向量作为测试样本以检验粒子群支持向量机强大的推演泛化能力，其中损伤的位置设置在平常连续刚构容易开裂处，其中包含梁端位置、每跨的1/8处和1/4处、以及跨中位置。

在结构未受损或是刚度不发生急剧变化时，结构的曲率模态差通常状况下会是一条光滑的曲线。一旦结构受损、刚度发生折减，原本光滑的曲线就会在损伤位置处发生突变。虽在在未受损出也会发生改变，但不会发生像受损位置一样的剧烈变化。故本文将把曲率模态差作为判定受损结构的损伤情况的参数。

(二)算例

洛清江大桥的模拟采用有限元软件Midas-civil。主桥的的上部结构单元按等长划分，共分为613个单元，主桥有限元模型图如图2所示。

图2 连续刚构有限元模型

测试样本的取值均为节点号与前三阶振型下数据处理后的曲率模态差，预测结果若为1则判定为连续刚构的相应节点位置位置发生了损伤，若为0则判定为该节点处结构未发生损伤。

为了证明算法的鲁棒性，测试样本中损伤程度新增了刚度折减为15%、25%、35%三种情况，此外损伤位置也不限于整座连续刚构的一半跨径，而是按全桥考虑损伤位置。根据支持向量机的分类结果来看，在对共计为15960个特征向量的测试样本中的各位置是否发生损伤进行判别，正确率为96.32%。

通过粒子群算法优化的适应度曲线MSE如图3所示，图中数值变化较为平缓且未出现明显的峰值说明识别效果较好。

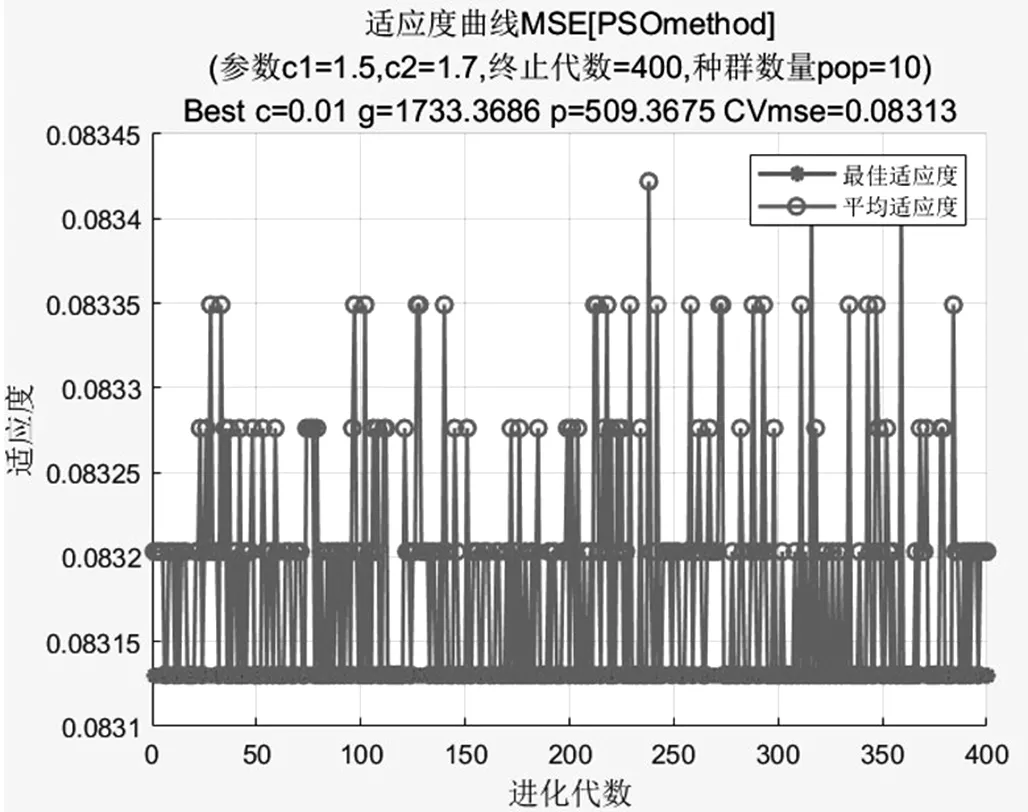
图3 参数寻优的适应度曲线

四、结论

损伤识别理论作为桥梁健康监测系统的重要组成部分，已经成为诸多工程技术人员研究的热点和焦点。选取曲率模态差作为本文中模拟的特征向量，将归一化后的曲率模态差作为特征向量输入粒子群优化的支持向量分类机当中训练，对桥梁损伤的位置进行判别结果表明，判别的正确率达到96.32%，损伤位置的判定效果较好。