基于遗传算法的工程项目群工期-费用优化研究

丰景春，施嘉锋，丰 慧，张 可

（1.河海大学商学院,江苏南京 211106；2.河海大学项目管理研究所，江苏南京 211106；3.江苏省世界水谷与水生态文明协同创新中心，江苏南京 211106；4.河海大学国际河流研究中心，江苏南京 211106）

1 文献综述

近年来，伴随着“一带一路”倡议、京津冀协同发展等重大方略的实行，我国稳步迈入经济发展新常态，我国承建的各种大中型工程项目也不再仅限于国内，同时也在走出国门，这意味着我国承担大中型建设工程项目的企业会面临更多的机遇与挑战，提高大中型工程建设项目的质量和效率，对建设工程项目管理进行优化，是亟待解决的问题。

建设工程项目管理优化的对象侧重于工期、费用和资源三大方面，这三大方面之间存在联系性，实现工程建设项目工期缩短（进度优化）、费用减少（成本优化）、资源均衡（资源优化）一直都是工程项目管理过程中的重要目标，在相关研究中，各专家学者的研究主要集中于实现单项目目标优化，例如，闫文周等［1］研究了关键链的期望工期、分布规律以及指定工期下的完工概率，以完工概率最小的关键链作为重点管控对象，从而实现工程项目工期优化；杨波等［2］利用决策网络计划技术在规定工期下对工程项目的费用进行优化；Pinha 等［3］认为糟糕的资源管理往往是工程项目超支以及工期延误的主要原因，因此提出了一种短期资源分配与管理的软件工具，以解决资源约束项目的资源调配问题。对于工程项目管理过程中资源均衡类问题，常用的衡量指标为资源均衡方差、绝对偏差等，如何立华等［4］提出了一个创新性指标——资源波动成本，可用以度量并最小化资源波动对施工生产力和成本造成的影响。也有研究把工程项目的质量纳入优化目标，一般来说，工程项目的质量难以量化，而高兴夫等［5］假定了工程项目活动时间与质量之间的线性关系，将活动的质量进行量化处理，构建了工期、费用、质量综合优化的数学模型。

以上研究多建立在工程建设单项目的基础上，而如今，绝大多数的工程项目不是孤立存在的，多是在项目群的环境下执行［6］。项目群是一系列旨在实现组织整体战略目标，且为适应于组织内外部环境变化而有机联结的各合同项目的集群。工程项目群相较于单一项目来说更为庞大，内部涉及更多的利益主体，工作关系错综复杂，对业主进度控制、费用控制等各方面的管理水平提出了更高的要求，因此，为保证项目群整体工作及时而又高效完工，以项目群的工期、费用、资源或质量为研究对象进行项目实施前和实施过程中的合理优化是十分必要的。

目前，工程项目群管理方面的研究提出了许多有价值的模型，例如，鉴于项目群内包含多个利益主体，丰景春等［7］引入了子网络的概念，将同一个承包商所承担的项目构成一个子网络，构建了项目群工期提前奖励模型，而汪玉亭等［8］研究了因承包人原因导致的子网络之间和子网络内项目工期延误对项目群所带来的影响，构建了基于子网络的项目群工期延误惩罚模型，奖励模型与惩罚模型对于项目群费用优化具有重要意义；丰景春等［9］建立了甲供资源约束条件下项目群实施前和实施过程中的工期-费用优化模型，分别用于优化初始网络计划以及优化后网络计划的动态调整，可以实现既定工期目标并控制业主支出费用；另外，项目群也需要调用资源以实现目标，丰景春等［10］考虑项目群内部合同项目之间的逻辑关系，利用资源在项目群内部合同项目之间的转移，构建资源约束条件下项目群工期优化模型。

工程建设单项目、多项目或者项目群中，各目标优化模型的求解一般多采用传统的关键路径法或关键链法，而如今，伴随着人工智能技术的发展，各种人工智能算法在众多领域得到了普及与应用，因而也出现了运用智能算法求解建设工程项目中不同目标优化问题的研究，例如，Chaharsooghi 等［11］构建了以项目现金流现值最大化为目标的数学优化模型，并使用遗传算法进行求解，该方法对项目现金流量的管理和项目控制有重要作用；张厚先等［12］利用粒子群算法求解了大型网络计划的工期固定资源均衡以及资源有限工期最短的优化问题；胡华选等［13］构造了一种改进的蚁群算法应用于工程项目的工期-费用优化问题，取得了有效的结果。以上的研究多为针对工程建设的单目标优化，也有学者进行了多个目标优化的研究，如Vijayan 等［14］利用多目标优化蚁群算法，实现了工程项目的时间、成本和风险3 个参数之间的协调优化；杜学美等［15］将质量和安全指标均进行了量化处理，连同工期和成本指标建立了多目标优化模型，并应用粒子群优化算法对模型进行求解，为求解多目标优化问题提供了指标处理以及算法求解的思路；邱惠［16］考虑到项目群资源共享，通过对工程项目群工期、成本、管理资源分析，提出基于粒子群算法的项目群网络计划优化模型，最后仿真验证优化效果；王益锋等［6］建立了项目群约束资源分配模型，引入了粒子群算法并给出算法在模型中的应用流程，对目标模型进行求解，实现了项目群整体进度的优化。

综上，现有研究成果对于求解工程项目群工期、费用或资源优化都具有重要的参考价值，与此同时，利用智能算法进行算例求解可以提高结果的精准性，是求解优化问题的可靠选择；但是现有研究主要是针对单项目而展开的，较少涉及项目群，同时现有研究成果鲜有利用智能算法求解项目群优化问题。为此，本文基于遗传算法基本原理构建了工程项目群工期-费用优化模型，以工程项目群费用最小作为主要优化目标，利用遗传算法对模型进行求解，并引入案例验证该模型及所使用算法的可行性。

2 工程项目群工期-费用优化机理分析

工程项目群（以下简称“项目群”）由多个相互关联的、拥有共同战略目标的项目与活动组成，通过对组成项目群的项目和活动进行整体管理，能够获得比对各项目单独管理更大的效益。工期、费用和资源作为项目群管理下易量化的指标，常被业主重点关注并列为管理导向目标之列。项目群工期、费用和资源之间虽各自独立，但也协调统一，若只对其中某一项进行优化而忽略其他因素，很大可能会得到一个损害其他管理目标的结果，三者互为制约作为优化目标达成的规制条件，且优化内容存在交叉重叠，因此，进行工程项目群优化时，工期、费用和资源彼此间的约束不容忽视。一般来说，项目群的整体费用包括各合同项目在执行过程中衍生的直接费用和间接费用两大项。在一定的工期范围内，项目群的直接费用随工期延长而降低，而间接费用不降反增，因此，两部分费用叠加之后得到的总费用存在一个最小值，即为业主所需支付费用的最小值，此时也会对应一个在此情形下的最小工期，所以在项目群费用优化过程中，不仅关注了费用目标的达成，同时还能实现工期目标的优化。

基于以上分析，本文构建的工期-费用优化模型以费用低作为首要目标构建目标函数，工期短作为次要目标可通过约束法被转化为模型中约束条件的一部分。其中，将项目群总体的费用划分为直接费用、工期压缩带来的赶工费用、项目群时间变化带来的奖惩以及间接费用；工期为关键线路上各项工作时间之和。使用约束法将次要目标转变为约束条件之后，可以将多目标优化问题转变为单目标优化问题，从而方便对模型进行求解。

3 优化模型构建

3.1 模型基本假设

对构建项目群的工期-费用优化模型涉及的一些参数或条件进行如下假设：

（1）项目群一共包含了N个合同项目，每个合同项目均包含n项工作。其中，关键路径上有q项工作，q项关键工作的集合为KR。各项工作间遵循严格的逻辑关系，优化不改变项目之间的逻辑关系。

（2）项目群内各项工作的工期不存在延误。在工程实践中，项目群内各个工作的工期可能提前也可能延误，为简化研究，假设项目群中各项工作不存在延误；无论是关键线路还是非关键线路上的工作，均在其工期可变动的范围内进行压缩。

（3）优化前项目群只有一条关键线路，优化后原关键线路仍为关键线路。

（4）项目群的工程质量在进行工期和费用优化的过程中不受影响。

3.2 模型构建

3.2.1 费用优化目标

项目群的费用优化需要调整工期来实现，费用一般由直接费和间接费两部分组成，其中直接费用会随工期的延长而减少，间接费则会随工期的延长而增加；考虑到工作赶工，因此引入赶工费率以及奖励与惩罚系数以充分表达项目群总费用（C）。项目群总费用包括正常情况下的直接费用、时间压缩时增加的直接费、项目群工期优化带来的奖励以及间接费用。因此构建以下目标函数：

3.2.2 工期约束条件

项目群的工期即为关键路径的长度，因此工期优化目标函数如下：

鉴于进行首要目标费用优化的同时工期也能得到优化，因此，通过约束法将各项工作的时间参数进行表示，作为费用优化过程中需要考虑的时间层面的约束条件。关键路径上的工作时间长短决定了最终工期的长短。对于关键路径上的工作，其实际用时应当较优化前更短，但需要控制在极限压缩范围内，即：

保持关键线路不变动，因此各条非关键路径上的工作持续时间之和不能超过关键路径的工期长度。

3.2.3 优化模型

基于以上目标函数与约束条件的构建与分析，得到如下工期-费用优化模型：

4 工期-费用优化的遗传算法

4.1 遗传算法选择依据

遗传算法（genetic algorithm，GA）是受生物学进化学说和遗传学理论的启发而发展起来的，是一类模拟自然生物进化过程与机制求解问题的自组织与自适应的人工智能技术，是一种借鉴生物界自然选择和自然遗传机制的随机的搜索算法。遗传算法在求解优化类问题，尤其是一些不能直接求解的复杂优化问题时能较好地解决问题。本文构建的模型以工作持续时间为变量，多个工作持续的时间与遗传算法中染色体上各个基因位编码可以相对应，优化过程中种群染色体的适应度函数可以利用模型的目标函数表示，因此使用遗传算法来求解项目群的工期-费用优化问题。

4.2 算法求解流程

（1）编码。利用遗传算法解决项目群工期-费用优化首先需要对问题进行编码，即将实际问题转化为一个利用遗传算法参数来表示的问题［17］。现从以下两方面说明编码时尤为重要的细节：一是被编码变量。将工作的持续时间作为被编码变量有利于项目群工期与费用的相关计算，每个基因位可与工作的编号相对应，即一个基因值对应一个工作的持续时间，工作的优先次序能体现出逻辑关系，因此本文选择工作持续时间作为编码变量且基因位与工作的编号相对应。二是基因值形式。由于二进制编码过长，不利于编辑和整理同时给解码工作造成困难，因此本文采用实数编码改进的遗传算法，以实数表示基因，直接使用问题的变量进行编码且不用转换进制，可节省整个算法迭代运行的时间。此外，由于实数可表示的范围大且精度高，对于结果更为有益。

（2）产生初始种群。根据编码机制，初始化原始种群，随机生成一定数目的个体，然后从中挑选出较好的个体加入到初始种群中。此过程是个不断迭代的过程，直到初始种群规模达到预期值。设定初始种群规模为100。

（3）适应度计算。遗传算法中，通过适应度函数值来衡量某一个体的适应度高低，适应度越高其繁殖机会越大；反之则越小。对于本文研究的项目群工期-费用优化问题，目标函数是求最小值，与遗传算法中适应度的原理刚好相反，为了保证遗传算法中对各个个体适应度的比较排序，从而确定选择概率，必须将目标函数转化为求最大值形式且函数值为非负的适应度函数，因此引入一足够大的常数c，使用该常数减去原目标函数，通过这样的构造方法即可转化为一个新的目标函数的最大化问题。

（4）选择。选择是指以一定概率从种群中选取若干个体的操作，是基于每个个体的适应度，按一定规则从某一代群体中选择出一些优良的个体遗传到下一代群体中的过程。本文采用轮盘赌选择算子，为有效应对“早熟收敛”问题，需要采用精英策略，即将当前群体中适应度最高的个体结构完整地复制到下一代群体中，优秀个体得到保留的同时也不会破坏种群的多样性。

（5）交叉。交叉也就是基因的重组，通过交换染色体上的基因完成。常用的交叉方法有单点交叉、多点交叉、均匀交叉等，本文采用均匀交叉，即对父代个体的部分染色体上的基因进行替换重组。设定交叉率pc为0.7。

（6）变异。变异指染色体上发生基因突变。变异算子是基因根据算子在取值范围内随机取值，然后替换该基因的原值个体。本文参考王云［18］研究中的变异算子（见表1），具体过程如下：在一条染色体中随机选择一个基因位置，如表1 中的基因值11，根据基因值大小范围随机选取一个值（不出现负值），即表1 中选择数值0.2，用选择的基因值加上这个值得到11.2，同时在染色体的对称位置选择基因并减去该值得到7.8，经调整后完成变异的全过程。设定变异率pm为0.01。

（7）终止条件。迭代次数的多少影响着运算以及收敛的速度，以最大迭代次数为终止条件，输出最终结果。设定终止迭代次数为500 次。

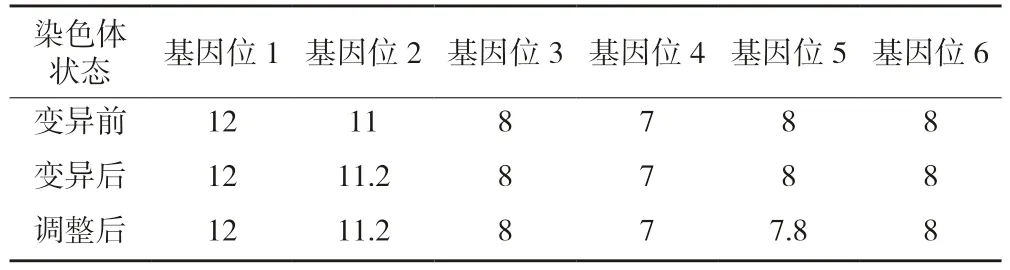
表1 变异算子

5 案例分析

5.1 案例背景

某Z 大型工程项目群包含有3 个合同项目，各合同项目内均有8 项工作，为了有效地实现Z 项目群进度的有效控制，业主绘制了网络计划，各项工作的持续时间如图1 所示，其中粗实线表示该工作位于关键路径上，即关键路径为A1—C1—F1—B2—F2—B3—F3—G3。由图1 可知，优化前Z 项目群的总工期为60 个月。

图1 Z 项目群网络计划分布

应业主的要求，现需要将项目群的工期进行压缩，从而使项目群提前建成投产，且由业主支付各项工作的赶工费用；同时，业主要求项目群提前完工时最终的总费用能控制在较小值。为简化计算，本文不考虑紧前工作提前完工、紧后工作提前开工产生的索赔费用，因此以Z 项目群最终提前完工时业主的奖励方式代替工作间的索赔费用，暂不考虑具体奖励费用的分配问题。各项工作的计划工期、最大可压缩月数、工程直接费用、赶工费率如表2所示，各项参数由项目经理、项目管理领域专家学者、专业技术人员根据Z 项目群特点共同综合决定。奖励系数β取值为60 万元/月，间接费用系数γ取值为90 万元/月。

表2 Z 项目群各工作相关参数

表2 （续）

5.2 项目群工期-费用优化模型求解

在Z 项目群的背景条件下，运用遗传算法对其进行工期-费用优化，以得到全局最优的项目群总费用，同时得到优化后对应费用的工期。本文运用Python 3.7.4 版本，通过运用遗传算法原理对Z 项目群工期-费用优化模型进行程序编写，运行得到如图2 所示结果。其中，横坐标代表的是子代数量，纵坐标为项目群在相应的算法迭代次数下的总费用。经过500 次的算法迭代，项目群总费用的最优值趋于全局最优值，即Z 项目群最优化费用为48 800 万元。在程序运行结束的界面，可以得到500 次迭代均为有效进化，且在第40 代时得到最优的一代。算法耗时0.927 秒，求解效率与精度较高。

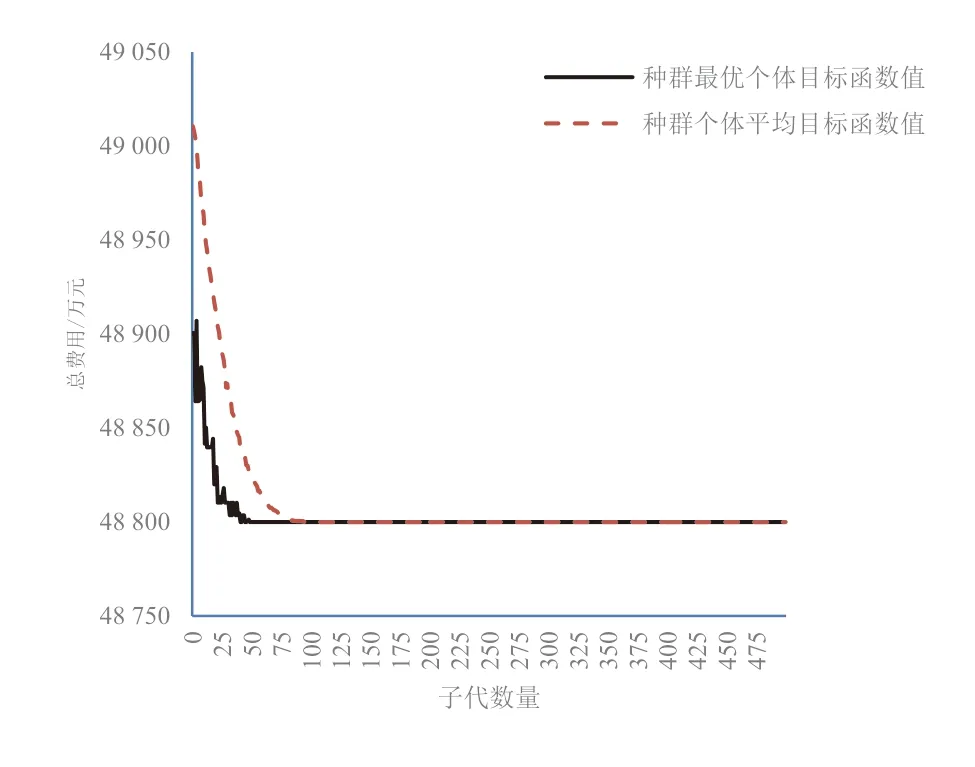
图2 基于遗传算法的Z 项目群工期-费用优化结果

对于模型的决策变量，即项目群内各项工作的持续时间，在算法迭代完成输出最优费用的同时，也输出项目群内各项工作的持续时间，得到的结果如表3 所示。通过与各项工作原来持续时间的比对，在优化过程中，合同项目1 各项工作的持续时间保持不变，而合同项目2 和3 中部分关键及非关键工作的持续时间发生了变化。通过计算，得到Z 项目群最终总工期为55 个月，比原计划工期缩短了5 个月，项目群工期缩短了8.33%。

表3 Z 项目群各项工作持续时间 单位：月

5.3 结果分析

（1）案例分析表明，Z项目群工期缩短了5个月，与此对应的项目群最终总费用为48 800 万元。若采用传统工期优化方法进行优化，则项目群总费用为54 394 万元，要比采用本研究提出的方法得到的最优费用要高出11.46%；同时，对应的项目群工期可以压缩14.5 个月，将原计划项目群工期压缩的幅度达到24.17%，这样大的工期压缩幅度对于原本就极为复杂的大型工程项目群管理工作带来更大困难，同时，需要耗费更多的人力、物力、财力，其操作性也较差，不符合实际情况。因此，在综合考虑工期、费用的情况下，采用本研究提出的方法求得的结果更符合大型复杂工程项目群的实际情况。

（2）根据变量最终取值情况，工期-费用优化的对象既包括关键工作，也包括部分非关键工作，据此得到费用最优条件下各项工作的工期。

5.4 模型优势

本文所建立的工程项目群工期-费用优化模型具有如下优势：

（1）是基于业主视角的项目群工期-费用优化模型。一方面，考虑了项目群中各项工作持续时间的变动给直接费与间接费带来的影响；另一方面，假定项目群内不存在工作延误的情况，考虑项目群提前竣工给承包商带来的奖励费用。在理想状态下，业主希望实现工期短、费用低，但在实际情况下，业主一味追求缩短工期往往会以降低工程质量为代价，因此，项目群工期-费用优化模型将费用优化作为首要目标，通过项目群总费用与工作持续时间之间的优化，使得项目群最终工期优于计划工期。

（2）模型构建在变量选择时充分运用遗传算法的原理，因此求解更加准确具体。项目群费用优化时全面考虑到了项目群中的所有工作，包括关键工作和非关键工作，由于可以人为设定输出结果的精确度，因此在编码操作过程中采用实数编码的方式，可以使变量的结果更加精确，操作也更为简便。

6 结论与展望

（1）鉴于大型工程项目群是一个复杂的系统，如果只对项目群中的单合同项目或项目群的局部进行优化，则项目群难以实现利益最大化，为此，需要从全局视角对项目群工期-费用进行优化。本文以合同项目中的每项工作工期作为变量，以总费用作为优化目标，构建了工程项目群工期-费用优化模型，运用实数编码以及精英保留策略的遗传算法，对项目群工期-费用优化模型进行求解，得到了项目群的最优总费用以及相对应条件下项目群中所有工作的工期。

（2）根据遗传算法的基本原理，通过对案例进行编程计算，求解得到各项工作的持续时间，在实现项目群总费用最优的同时，案例项目群的工期也比原先计划工期缩短了5 个月。案例求解表明，运用智能算法求解这一问题更加高效，得到的结果也更为精确。

本文构建的工程项目群工期-费用优化模型没有考虑资金的时间价值，而对于大型工程项目群，其工期一般历时较长，考虑资金的时间价值将更加符合工程实际；此外，项目群质量以及资源等方面也是项目群优化问题中需要考虑的重要指标，结合智能算法求解这系列问题还有待进一步研究。