台阶式溢洪道滑行流相对水力特性规律研究

马朋辉，胡亚瑾，刘韩生

（西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100）

1 研究背景

水利工程中为拦截水流、抬高水位或调蓄水量需修建闸、坝等挡水建筑物。挡水建筑物建成后上下游形成水头差，从而使过堰或过坝水流形成巨大的能量。为了消除过堰或过坝所形成的水流能量，传统工程中都是利用光滑溢洪道或溢流坝进行挑流消能或在下游修建消力池进行水跃消能。为了防止产生空蚀破坏，需要对这种光滑溢洪道或溢流坝的局部不平整度（特别是垂直水流方向的局部不平整度）作出严格的规定[1]。

近30 多年来，随着碾压混凝土筑坝技术的出现和应用，对传统溢洪道和溢流坝的体型设计产生了很大的影响。台阶式溢洪道、溢流坝是随碾压混凝土筑坝施工技术的发展而兴起的一种泄洪消能设施，是在光滑溢洪道的基础上演变而来的，并以其优于光滑溢洪道、溢流坝的消能率而受到世界各国水利科研工作者的关注。台阶式溢洪道上的水流根据单宽流量、台阶高度及坡度的不同，会出现跌落流、滑行流及过渡流3种流态。水利工程中多以出现滑行流进行台阶式溢洪道的设计，跌落流常出现在泄流流量较小的情况，过渡流因其流态不稳定而应尽量避免。国内外学者对台阶式溢洪道进行了大量的试验研究，目前的研究主要集中在台阶式溢洪道滑行流的消能特性方面，研究成果颇多[2-12]，但由于台阶水流复杂，尚未得到一致结论。

流速、弗劳德数及消能率是台阶式溢洪道的重要水力参数，对其进行研究具有重要意义。目前对于台阶断面流速的研究多采用半经验半理论计算方法[13-15]和数学模型法[16-17]。关于弗劳德数，以往常与消力池一并研究[18-20]，对台阶式溢洪道弗劳德数的研究通常只针对某一断面[10，21-22]，缺乏系统性的研究成果。张峰等[23]和刘士和[24]以流速为依据对台阶式溢洪道相对消能作了一些探讨。张志昌等[4]提出台阶式溢洪道消能与弗劳德数有关，但未作深入研究。

本文基于光滑溢洪道水力计算理论已经成熟，其各水力参数可以直接通过计算得到，因此将台阶式溢洪道与同体型的光滑溢洪道进行对比研究，定义了相对流速、相对弗劳德数及相对消能率3个相对水力参数。通过模型试验，首先分析台阶式溢洪道常规水力参数的沿程变化规律及相对临界水深、坡度对常规水力参数的影响；然后采用同样的数据分析相对水力参数的沿程变化规律及相对临界水深、坡度对相对水力参数的影响，进而论证引入台阶式溢洪道相对水力参数的必要性。

2 试验设计、测量方法及水流流态

对3个工程项目的台阶式溢洪道进行水工模型试验，试验基本资料见表1。

表1 模型试验资料

试验一至试验三均采用重力相似准则设计，试验最小雷诺数均大于500，表明流态均为紊流。试验中台阶式溢洪道阶顶断面水深采用测针多次量测后取平均值，流量采用三角形堰或矩形薄壁堰进行量测。

台阶式溢洪道上的水流流态根据相对临界水深hk/d（hk为溢洪道进口处临界水深，d为台阶高度）及坡度可分为三类，即跌落流、滑行流及过渡流[1]。当相对临界水深或坡度较大时，水流流过台阶表面，各台阶内部全部被水充填，没有空腔存在，并在各台阶隅角和主流之间形成一个横轴旋涡，靠近主流处，旋涡旋转方向与主流方向一致，这种水流称为滑行流。当相对临界水深或坡度较小时，水流在每一个台阶上自由跌落，并且在跌落水舌与台阶水垫之间总是形成一个空腔，台阶空腔内有自由水面形成，这种水流称为跌落流。过渡流是在滑行流和跌落流之间形成的一种水流流态，在有些台阶内出现空腔，但在另一些台阶内则出现旋涡水流。

Chanson[25]、Chamani 等[26]、Yasuda 等[27]和田嘉宁[28]都对台阶式溢洪道的水流流态进行了研究，并给出了划分滑行流和跌落流的经验公式。Yasuda 提出的公式介于Chanson和田嘉宁公式之间，滑行流下限、跌落流上限的经验公式分别如下[27]：

其中

式中：hk为临界水深，m；d为台阶高度，m；θ为台阶式溢洪道坡度，（°）；q为单宽流量，m2/s；g为重力加速度，m/s2。

采用观察及上述经验公式相结合的方法进行判断，试验中台阶式溢洪道的水流流态均为滑行流。本文研究的是台阶式溢洪道非均匀流段水力参数变化规律，后文中采用的数据均来自非均匀流段。台阶式溢洪道上水流达到准均匀流所需的垂直高度Hdam，u可以采用下式估算[21]：

3 相对流速、相对弗劳德数、相对消能率的定义及计算

流速及弗劳德数是重要的水力参数，消能率是台阶式溢洪道研究的热点和重点。弗劳德数表示过水断面上单位重量液体所具有的平均动能与平均势能的比值；消能率表示过水断面上累计消耗能量占来流总能量的比值，即溢洪道来流总能量减去断面剩余能量，比上溢洪道来流总能量，可以写为：

式中：Et为溢洪道来流总能量，m；Er为溢洪道过水断面剩余能量，m；Ed为溢洪道过水断面累计消耗能量，m。

为深入研究台阶式溢洪道的水力特性，本文分别引入了相对流速、相对弗劳德数及相对消能率。定义台阶式溢洪道某一断面位置的相对流速Δv为与其断面位置相对应的光滑溢洪道流速vg与台阶式溢洪道同一断面流速vt之差；台阶式溢洪道某一断面位置的相对弗劳德数ΔFr为与其断面位置相对应的光滑溢洪道弗劳德数Frg与台阶式溢洪道同一断面弗劳德数Frt之差；台阶式溢洪道某一断面位置的相对消能率Δη为该断面的总消能率ηt与相对应的光滑溢洪道同一断面消能率ηg之差。

根据定义，任意断面位置的相对流速、相对弗劳德数及相对消能率分别为：

图1为台阶式溢洪道及对应的光滑溢洪道体型示意图。图1中台阶式溢洪道1"-1"断面和与之对应的光滑溢洪道1-1 断面互为对应断面，台阶式溢洪道1"-1"断面的水深h1"和与之对应的光滑溢洪道1-1 断面水深h1互为对应水深，台阶式溢洪道1"-1"断面的流速v1"和与之对应的光滑溢洪道1-1 断面流速v1互为对应流速，台阶式溢洪道1"-1"断面的弗劳德数Fr1"和与之对应的光滑溢洪道1-1 断面弗劳德数Fr1互为对应弗劳德数，台阶式溢洪道1"-1"断面的能量E1"和与之对应的光滑溢洪道1-1 断面的能量E1互为对应能量。

则图1中台阶式溢洪道1"-1"断面的相对流速、相对弗劳德数及相对消能率可以分别写为：

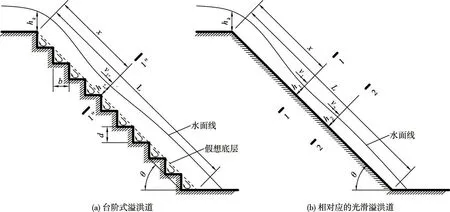
图1 台阶式溢洪道及相对应的光滑溢洪道示意

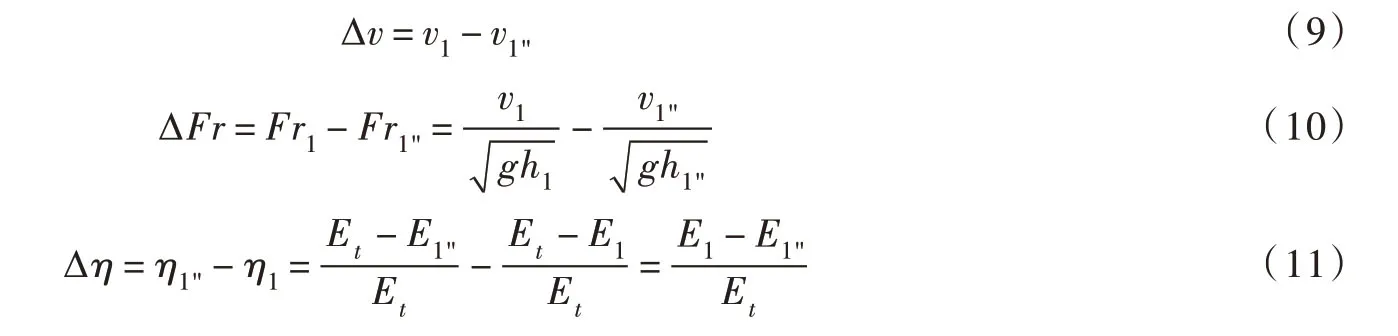
台阶式溢洪道的水深采用测针多次测量取平均值，断面平均流速采用实测单宽流量除以断面平均水深求得，进一步计算可得台阶式溢洪道断面弗劳德数及消能率。

光滑溢洪道水深采用能量方程，根据分段求和法计算[29]，光滑溢洪道流速、弗劳德数及消能率的计算同上述台阶式溢洪道。采用分段求和法计算光滑溢洪道水深的方法具体如下：

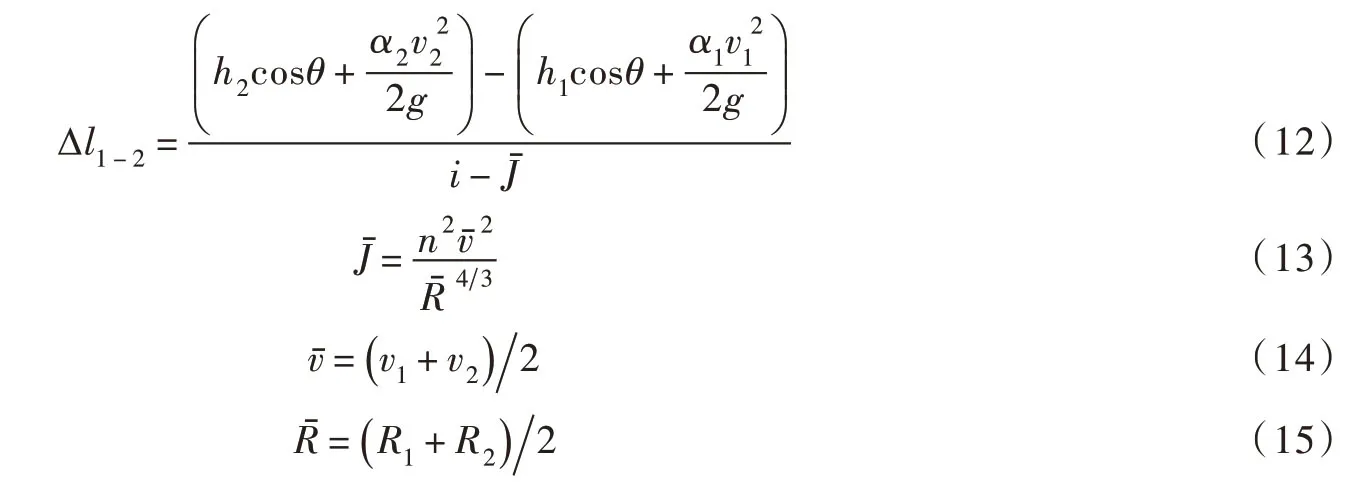
式中：Δl1-2为分段长度，m；h1、h2分别为分段始末断面水深，即图1中光滑溢洪道1-1 断面和2-2断面的水深，m；v1、v2分别为分段始末断面平均流速，即图1中光滑溢洪道1-1 断面和2-2 断面的平均流速，m/s；α1、α2为流速分布不均匀系数，取1.05；θ为溢洪道坡度，（°）；i=sinθ；Jˉ为分段内平均摩阻坡降；n为溢洪道糙率系数，取为0.014；vˉ为分段平均流速，m/s；Rˉ为分段平均水力半径，m。

4 台阶式溢洪道水力特性规律

4.1 台阶式溢洪道常规水力特性规律对3个模型试验项目在不同工况下的沿程阶顶过流断面平均流速、弗劳德数及消能率进行计算，分别分析其沿程变化规律及相对临界水深、溢洪道坡度对其的影响。

4.1.1 流速沿程变化规律 台阶式溢洪道阶顶过流断面平均流速沿程变化情况如图2所示。图2（a）以试验二的资料（θ=32.0°，d=0.6 m，q=8.77 m2/s、11.80 m2/s、24.09 m2/s）为依据，分析相对临界水深对流速的影响。图2（b）以试验三的资料（θ=38.7°，q=46.58 m2/s，d=0.5 m、2.0 m）为依据，分析相对临界水深对流速的影响。图2（c）以试验三的资料（θ=38.7°，d=1.0 m，q=21.20 m2/s、35.72 m2/s、46.67 m2/s、62.18 m2/s）为依据，分析相对临界水深对流速的影响。图2（d）以试验一（θ=26.6°，d=1.0 m，q=15.37 m2/s、35.72 m2/s）及试验三（坡度θ=38.7°，d=1.0 m，q=35.72 m2/s；d=2.0 m，q=46.58 m2/s）的资料为依据，分析坡度对流速的影响。

由图2可以得出，台阶式溢洪道阶顶过流断面平均流速沿程呈现先增大后减小的趋势，这是由台阶式溢洪道上特殊的水流流态所决定的。在台阶式溢洪道足够长的情况下，其上水流沿程可以划分为非掺气区、掺气发展区及掺气充分发展区。在非掺气区，台阶式溢洪道水深沿程减小，水流平均流速沿程增大；在掺气发展区，水流掺气沿程增加，掺气水深亦沿程增大，水流平均流速沿程减小；当全断面掺气浓度达到一致时为掺气充分发展区，水流掺气水深及平均流速沿程不变。图2（a）所选取的测量断面均位于非掺气区，因此水流平均流速沿程增大。其它试验资料中，台阶式溢洪道阶顶过流断面平均流速沿程变化均表现出相同的规律。

图2 流速沿程变化规律

由图2（a）—（c）可以得出，台阶式溢洪道阶顶过流断面平均流速随相对临界水深的增大而增大。为分析坡度对台阶式溢洪道流速的影响，首先选取试验一（θ=26.6°，d=1.0 m，q=35.72 m2/s）和试验三（θ=38.7°，d=1.0 m，q=35.72 m2/s）中的两组数据进行对比，所选两组数据的相对临界水深相同，可以进行单因素分析。再次选取试验一（θ=26.6°，d=1.0 m，q=15.37 m2/s）和试验三（θ=38.7°，d=2.0 m，q=46.58 m2/s）中的另两组数据进行对比，相对临界水深分别为2.9和3.0，差别很小，可以采用单因素分析近似处理。由图2（d）可以得出，坡度对流速的影响复杂，规律性差，不便分析。

综上，台阶式溢洪道阶顶过流断面平均流速沿程呈复杂的曲线变化规律，相对临界水深及坡度对平均流速的影响也较为复杂，不便分析应用。

4.1.2 弗劳德数沿程变化规律 台阶式溢洪道阶顶过流断面弗劳德数的大小受断面水深及断面平均流速的影响，在非均匀流段，断面水深及断面平均流速沿程均呈复杂的曲线变化规律。台阶式溢洪道阶顶过流断面弗劳德数沿程变化情况如图3所示。图3分析所选用的试验资料与图2完全相同。由图3可以得出，整体上，台阶式溢洪道阶顶过流断面弗劳德数沿程呈现先增大后减小的趋势。其它试验资料中，台阶式溢洪道阶顶过流断面弗劳德数沿程变化均表现出相同的规律。由于受断面水深及断面平均流速的双重影响，相对临界水深及溢洪道坡度对台阶式溢洪道阶顶过流断面弗劳德数的影响较为复杂，未能总结出明显的规律。

综上，台阶式溢洪道阶顶过流断面弗劳德数沿程呈复杂的曲线变化规律，相对临界水深及坡度对弗劳德数的影响也较为复杂，不便分析应用。

4.1.3 消能率沿程变化规律 台阶式溢洪道消能率沿程变化情况如图4所示。图4分析所选用的试验资料与图2完全相同。由图4可以得出，台阶式溢洪道消能率沿程逐渐增大，且递增梯度也沿程逐渐增大，说明台阶式溢洪道的消能效果沿程逐渐增强。由图4（a）—（c）可以得出，台阶式溢洪道消能率随相对临界水深的增大而减小。由图4（d）可以得出，台阶式溢洪道消能率随坡度的增大而增大，即台阶对水流能量的消耗作用随溢洪道坡度的增大而增强。

综上，台阶式溢洪道消能率沿程逐渐增大，且递增梯度也沿程逐渐增大；消能率随相对临界水深的增大而减小，随坡度的增大而增大。

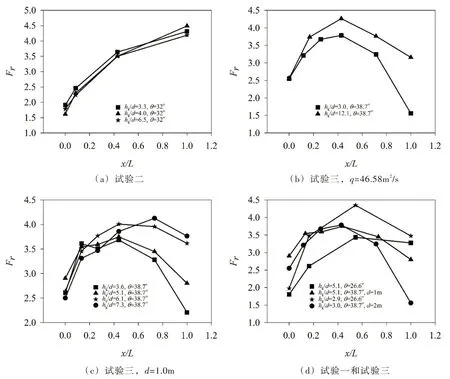
图3 弗劳德数沿程变化规律

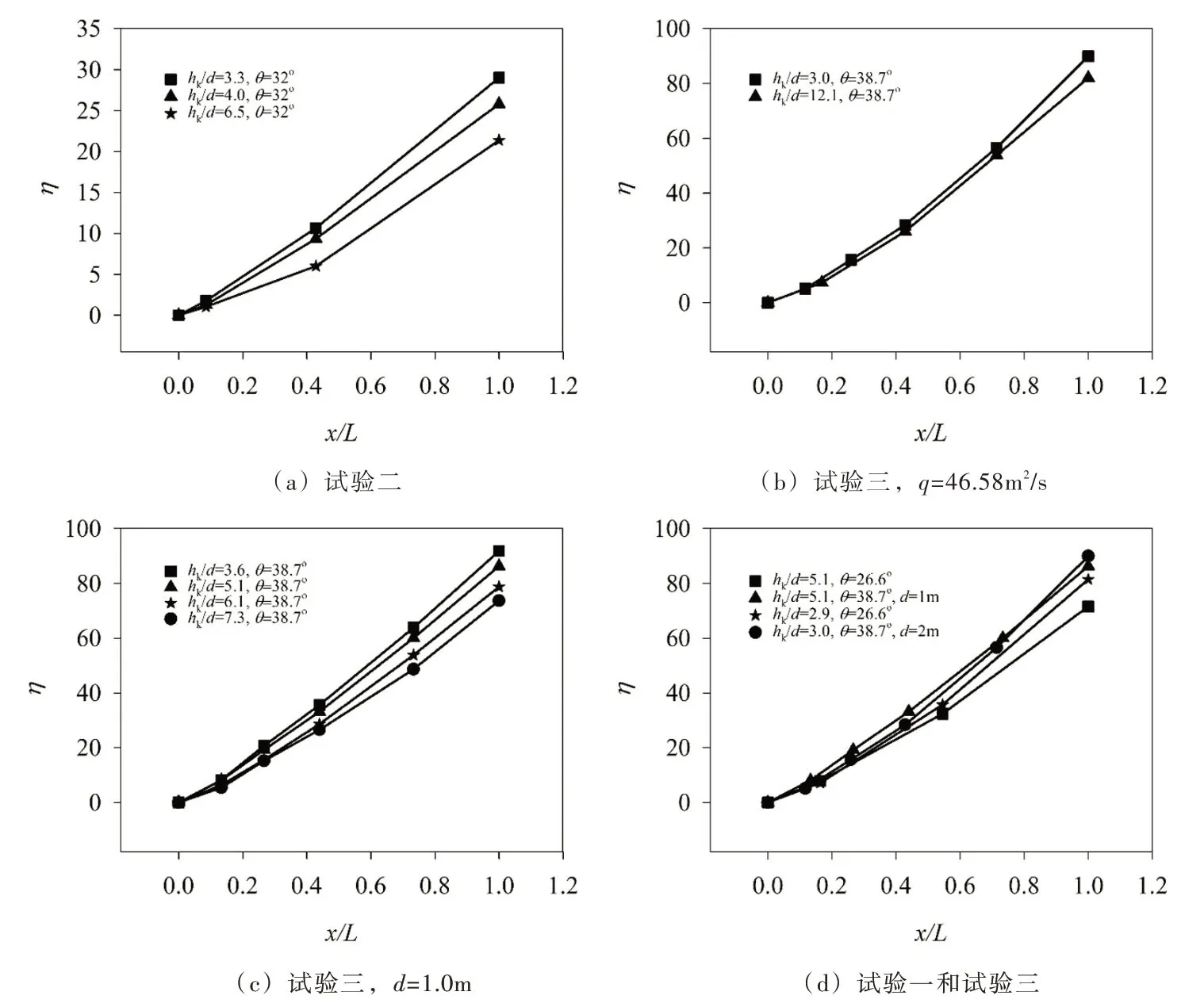
图4 消能率沿程变化规律

4.2 台阶式溢洪道相对水力特性规律对3个模型试验项目在不同工况下的沿程阶顶过流断面相对流速、相对弗劳德数及相对消能率进行计算，并分别分析其沿程变化规律及相对临界水深、溢洪道坡度对其的影响。台阶式溢洪道相对水力特性分析所选用的试验资料与前述常规水力特性分析所选用的试验资料完全相同。

4.2.1 相对流速沿程变化规律 台阶式溢洪道阶顶过流断面相对流速沿程变化情况如图5所示。由图5可知，台阶式溢洪道阶顶过流断面相对流速沿程表现出良好的线性相关关系，相关系数平均值为0.9887，最小值为0.9729，最大值为0.9977。台阶式溢洪道阶顶过流断面相对流速沿程线性递增，这是由于溢洪道上沿程设置的为均匀、等高台阶，在滑行流流态下，各处台阶对水流流速的阻碍作用是相同的，台阶式溢洪道某一断面的相对流速实际上是前面单个台阶对水流流速的阻碍作用之和。

运用反应谱分析方法研究了津保桥整桥和裸塔在E1、E2地震响应荷载下的动态响应，得出的结论进行对比分析得出主要结论。

由图5（a）—（c）可以得出，台阶式溢洪道同一阶顶过流断面相对流速随相对临界水深的增大而减小。具体地，当相对临界水深由3.3 增大至6.5，相对流速减小了25.87 %～48.45 %（试验二）；当相对临界水深由3.0 增大至12.1，相对流速减小了16.08 %～28.97 %（试验三，q=46.58 m2/s）；当相对临界水深由3.6 增大至7.3，相对流速减小了20.72 %～41.95 %（试验三，d=1.0 m）。由图5（d），通过两组不同的对比数据均可以得出，坡度大时所对应的直线斜率大，坡度小时所对应的直线斜率小，因此台阶式溢洪道阶顶过流断面相对流速随坡度的增大而增大。具体地，当坡度由26.6°增大至38.7°，相对流速分别增大了43.08 %～87.88 %（hk/d=5.1）和26.68 %～75.46 %（hk/d=3.0）。由相对流速的定义可知，相对流速是指由于台阶的存在使台阶式溢洪道上某一断面水流流速相对于同体型光滑溢洪道同一断面流速的减小值，因此可以得出台阶对水流流速的阻碍作用在量值上随相对临界水深的增大而减小，随坡度的增大而增大。

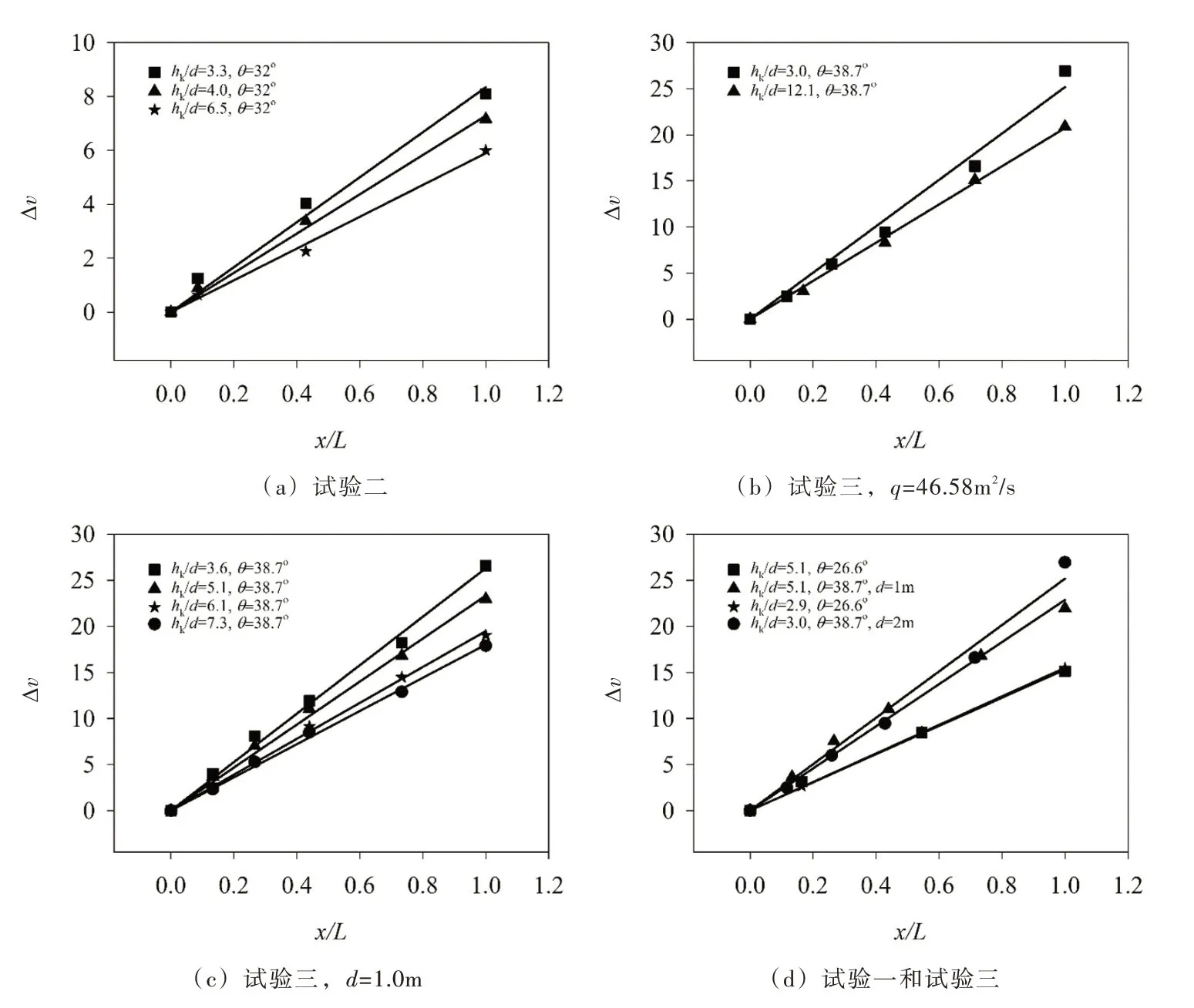
图5 相对流速沿程变化规律

综上，台阶式溢洪道阶顶过流断面相对流速沿程线性递增，随相对临界水深的增大而减小，随坡度的增大而增大。

4.2.2 相对弗劳德数沿程变化规律 台阶式溢洪道阶顶过流断面相对弗劳德数沿程变化情况如图6所示。由图6可知，台阶式溢洪道阶顶过流断面相对弗劳德数沿程表现出良好的线性相关关系，相关系数平均值为0.9944，最小值为0.9855，最大值为0.9998。台阶式溢洪道阶顶过流断面相对弗劳德数沿程线性递增，这是由于溢洪道上沿程设置的为均匀、等高台阶，在滑行流流态下，各处台阶对水流弗劳德数的减小值是相同的，台阶式溢洪道某一断面的相对弗劳德数实际上是前面单个台阶对水流弗劳德数的减小值之和。

由图6（a）—（c）可以得出，台阶式溢洪道同一阶顶过流断面相对弗劳德数随相对临界水深的增大而减小。当相对临界水深由3.3 增大至6.5，相对弗劳德数减小了50.7 %～65.14 %（试验二）；当相对临界水深由3.0 增大至12.1，相对弗劳德数减小了11.46 %～34.25 %（试验三，q=46.58 m2/s）；当相对临界水深由3.6 增大至7.3，相对弗劳德数减小了45.13 %～62.02 %（试验三，d=1.0 m）。由图6（d），通过两组不同的对比数据均可以得出，坡度大时所对应的直线斜率大，坡度小时所对应的直线斜率小，因此台阶式溢洪道阶顶过流断面相对弗劳德数随坡度的增大而增大。具体地，当坡度由26.6°增大至38.7°，相对弗劳德数分别增大了74.00 %～103.72 %（hk/d=5.1）和13.15 %～29.30 %（hk/d=3.0）。由相对弗劳德数的定义可知，相对弗劳德数是指由于台阶的存在使台阶式溢洪道上的某一断面水流弗劳德数相对于同体型光滑溢洪道同一断面弗劳德数的减小值，因此，由于台阶的存在而使水流弗劳德数的减小在量值上随相对临界水深的增大而减小，随坡度的增大而增大。

图6 相对弗劳德数沿程变化规律

综上，台阶式溢洪道阶顶过流断面相对弗劳德数沿程线性递增，随相对临界水深的增大而减小，随坡度的增大而增大。

4.2.3 相对消能率沿程变化规律 台阶式溢洪道相对消能率沿程变化情况如图7所示。由图7可知，台阶式溢洪道相对消能率沿程表现出良好的线性相关关系，相关系数平均值为0.9928，最小值为0.9752，最大值为0.9998。台阶式溢洪道相对消能率沿程线性递增，这是由于溢洪道上沿程设置的为均匀、等高台阶，在滑行流流态下，各处台阶所增加的水流能量损耗是相同的，台阶式溢洪道某一断面的相对消能率实际上是前面单个台阶消能率之和。

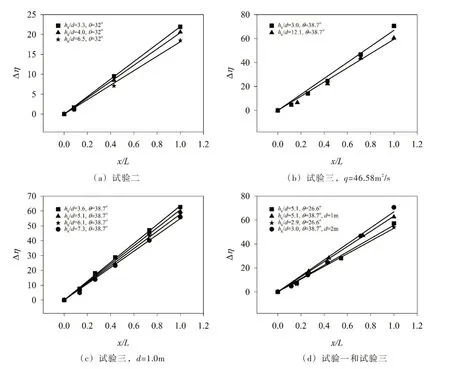
图7 相对消能率沿程变化规律

由图7（a）—（c）可以得出，台阶式溢洪道同一阶顶过流断面相对消能率随相对临界水深的增大而减小。具体地，当相对临界水深由3.3 增大至6.5，相对消能率减小了15.52 %～21.36 %（试验二）；当相对临界水深由3.0 增大至12.1，相对消能率减小了7.85 %～20.05 %（试验三，q=46.58 m2/s）；当相对临界水深由3.6 增大至7.3，相对消能率减小了11.11 %～34.65 %（试验三，d=1.0 m）。由图7（d），通过两组不同的对比数据均可以得出，坡度大时所对应的直线斜率大，坡度小时所对应的直线斜率小，即台阶式溢洪道阶顶过流断面相对消能率随坡度的增大而增大。具体地，当坡度由26.6°增大至38.7°，相对消能率分别增大了10.23 %～21.34 %（hk/d=5.1）和4.73 %～30.85 %（hk/d=3.0）。由相对消能率的定义可知，相对消能率是指由于台阶的存在使台阶式溢洪道上的某一断面消能率相对于同体型光滑溢洪道同一断面消能率的增加值，因此，由于台阶的存在而使消能率的增加值随相对临界水深的增大而减小，随坡度的增大而增大。

综上，台阶式溢洪道阶顶过流断面相对消能率沿程线性递增，随相对临界水深的增大而减小，随坡度的增大而增大。

5 结论

通过3个不同的水工模型试验，分析了台阶式溢洪道常规水力参数沿程变化情况及相对临界水深、坡度对其的影响。结果表明，台阶式溢洪道阶顶过流断面平均流速、弗劳德数沿程呈先增大后减小的趋势；平均流速随相对临界水深的增大而增大，未能总结出弗劳德数随相对临界水深变化的规律，亦未能总结出平均流速及弗劳德数随坡度变化的规律；台阶式溢洪道消能率沿程逐渐增加，且递增梯度沿程逐渐增大；消能率随相对临界水深的增大而减小，随坡度的增大而增大。总体上来讲，台阶式溢洪道常规水力参数关系复杂，规律性不强，不便分析应用。

通过将台阶式溢洪道与光滑溢洪道进行对比，引入台阶式溢洪道相对水力参数，分析了相对水力参数沿程变化情况及相对临界水深、坡度对其的影响。结果表明，台阶式溢洪道阶顶过流断面相对流速、相对弗劳德数、相对消能率沿程均表现出较好的线性相关关系，线性相关系数分别为0.9729～0.9977、0.9855～0.9998和0.9752～0.9928；相对流速、相对弗劳德数及相对消能率均随相对临界水深的增大而减小，随坡度的增大而增大。通过对台阶式溢洪道相对水力参数沿程线性规律的定量分析，并结合光滑溢洪道成熟的水力计算理论，可以得出台阶式溢洪道沿程各断面水力参数值，为台阶式溢洪道水力计算提供了新方法。

鉴于台阶式溢洪道相对水力参数所呈现的较强的规律性及光滑溢洪道水力计算理论的成熟性，有必要引入台阶式溢洪道相对水力参数，这对于认识、分析和应用台阶式溢洪道有着重要的现实意义。