混凝土类材料弹塑性损伤问题的全隐式迭代法

张 立，李广凯，马怀发

（1.山东泰山抽水蓄能电站有限责任公司，山东 泰安 271000）

（2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038）

（3.中国水利水电科学研究院 工程抗震研究中心，北京 100048）

1 研究背景

混凝土类材料一般具有初始微缺陷或微孔洞，在外载荷作用下混凝土类材料内部的微孔洞、微裂纹等初始缺陷延长、扩展、交汇，从而形成微裂缝。微裂缝引起材料刚度劣化和强度降低。同时，微裂缝界面的摩擦滑动引起类似于金属材料的晶格位错，产生不可恢复残余（塑性）变形[1-3]。基于金属晶体滑移或位错发展起来的弹塑性力学，能够较好地描述混凝土类材料的弹性变形、破坏条件以及不可恢复变形的演化发展。尽管混凝土类材料的破坏机理与金属材料有所不同，但塑性理论在处理不可恢复变形具有显著优势，且损伤力学可以很好地描述其内部微缺陷或微裂缝的演化规律及其对其宏观力学性能的影响，二者结合形成的弹塑性损伤模型可以全面地描述混凝土类材料的非线性变形特征[4-6]。弹塑性问题是典型的材料非线性问题，其应力一般与变形或加载历史有关，需要采用增量法求解。因此，增量应力应变本构方程与迭代法相结合被广泛应用于求解弹塑性问题。牛顿-拉斐逊法包括N-R和mN-R 算法，是求解非线性方程组最常用的增量迭代法。人们为了改善收敛速度提出了各种加速迭代的措施，艾特肯加速法[7]和线性搜索法[8-11]与牛顿法结合使用，以减少计算迭代次数。但这些算法都需要刚度矩阵显式表达形式，往往还受限于本构方程的积分形式。与上述方法不同的是，弹塑性隐式全迭代法[12]能够联立求解弹塑性问题的平衡方程、屈服函数和塑性流动方程，不需要刚度矩阵的显式形式，也不拘泥于变形的增量和全量形式，并且不受屈服函数和塑性流动方程具体形式的限制，可扩展应用于求解混凝土类材料的非线性问题。

在极限荷载作用下，混凝土类材料的非线性变形一般伴随着损伤演化和塑性流动的过程，即为弹塑性损伤过程。基于应变等效假定[13-15]，在有效应力空间利用塑性力学方法，用有效应力张量代替经典塑性力学中的柯西（名义/实际）应力张量，以考虑不可恢复变形。由于有效应力随着弹性应变的增加而单调增加，屈服面处于膨胀状态，不会出现柯西应力空间材料软化所导致的屈服面收缩情况，因此，只需考虑应力强化，避开了处理应变软化的问题。

本文首先介绍弹塑性问题的全隐式迭代法的基本思想，再引入局部回映迭代，以改进其收敛性。然后，基于混凝土类材料弹塑损伤变形特性及其在有效应力空间应力强化的特点，将混凝土类材料弹塑性损伤问题分解为弹塑性问题和损伤问题。在有效应力空间上采用弹塑性全隐式迭代法求解其弹塑性变形，由损伤参数描述材料刚度的弱化，并将有效应力转换为物理空间的实际（名义）应力。这种求解方法即为本文提出的混凝土类材料弹塑性损伤问题的全隐式迭代法。

2 全隐式迭代法的基本思想

弹塑性材料的本构关系通常由屈服函数和流动规律以增量形式给出。本构关系一般表示为一种显式形式，Δσ=DepΔε，其中的Δσ、Δε分别为应力增量和应变增量，Dep为弹塑性矩阵。弹塑性矩阵与加载过程有关，将根据应力应变状态进行调整。本文提出的全隐式迭代法的基本思想是将含有塑性因子未知量的屈服条件和塑性流动方程作为基本方程，并与平衡方程联立，通过隐式迭代求解变形及其相关物理量。假设εn、εp n、σn和Δλn分别是第n个加载步的应变、塑性应变、应力和塑性因子。在n+1个加载步，求解描述弹塑性问题的方程组为：

式中：Y为屈服函数，是应力和内变量κ 的函数；G为塑性流动势函数；F为外分布荷载。

在n+1 加载步的应变增量为Δεn、塑性应变增量Δεp n、内变增量Δκn和应力增量Δσn，则总应变、塑性应变、应力以及内变量分别表示为：

其中De为弹性矩阵。

令：

塑性因子的计算公式为：

将式（6）代入式（3），可以得到：

即：

其中弹塑性矩阵为：

如果Yn=0，应力增量为：

式（1）中的第一个方程即平衡方程，可以表示为：

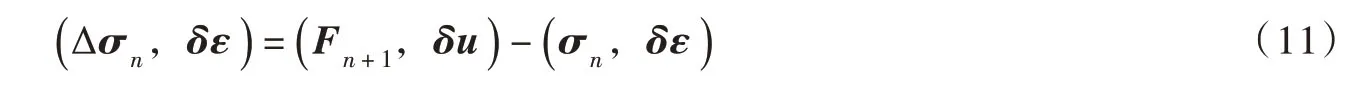
将式（3）代入式（11），可以得到：

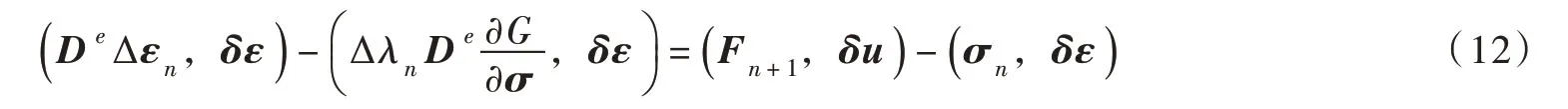
将式（6）代入式（12），并消去Δλn，就得到求解弹塑性问题基本方程的积分弱解形式：

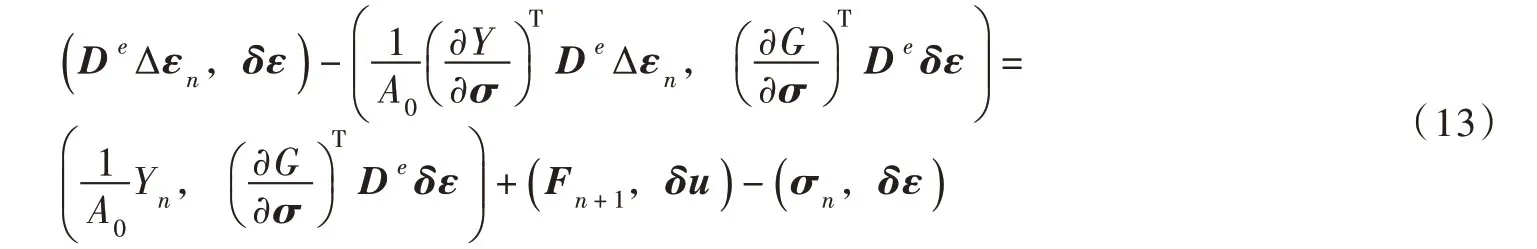
3 弹塑性问题的全隐式迭代法

3.1 求解弹塑性方程的隐式迭代格式式（13）是式（1）的等价弱解形式。在弹性加载或塑性卸载时，塑性因子Δλn小于零，则将式（13）就转化为线性弹性方程：当应力状态处于塑性区时，塑性因子Δλn大于零，则需要求解弹塑性方程。

在每一加载步内，保持外部荷载为常量，第k迭代步的方程（13）有如下形式[12]：

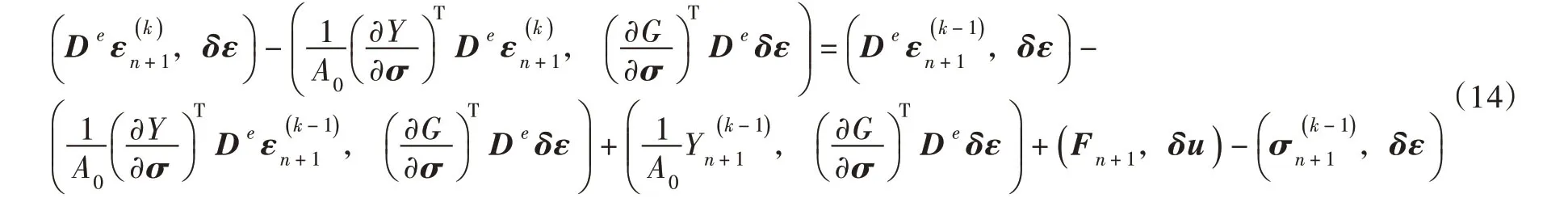
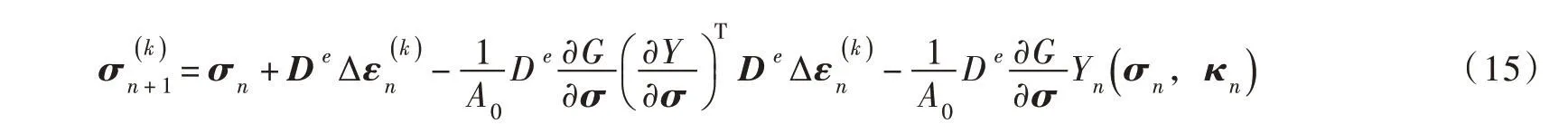
传统的弹塑性问题求解，一般按式（8）计算弹塑性矩阵，按式（9）求解应力增量。与传统方法不同，本文的隐式迭代法不需用显式求出弹塑性矩阵，总应力和应力增量在迭代过程结束由式（15）自动给出。式（14）的迭代格式是全量的形式，这样在解决实际问题时其边界条件可以用全量的形式给出。

3.2 回映迭代法上述迭代法认为，当时可以通过平衡方程迭代式的右端项拉回到屈服面，即当迭代式（14）收敛时，如果则且有即可得到方程的平衡形式：当应力进入屈服状态，迭代过程实质际上是应力回归屈服面的过程，也是应力重分布的过程。

如图1所示的受集中荷载作用的简支梁，梁跨度为2l，高度为2h，厚度为b，跨中受集中荷载P作用，若梁的材料为理想弹塑性，并服从Mises 屈服准则，按照塑性理论可知，当梁跨中横截面弹性高度he =h，即跨中横截面完全处于弹性状态，弹性极限弯矩当he =0，即跨中横截面处于完全塑性状态，已形成塑性铰，此时塑性极限弯矩则有在塑性极限弯矩作用下形成塑性铰时，有如图1所示的屈服塑性区。其塑性区边界为在梁的上、下边缘离跨中距离处，he =h，塑性区在上下边缘的宽度为梁长度的但按式（14）模拟得到如图2的屈服塑性区，由于应力过于集中，超极限应力不再收敛到屈服面，此时的计算得到塑性区与理论解差别较大。

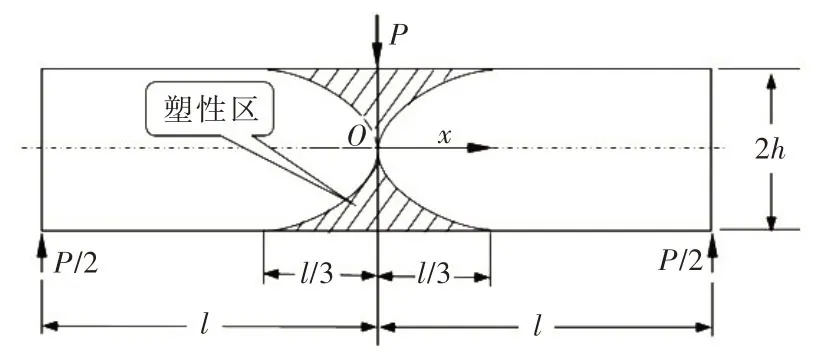
图1 集中荷载作用下简支梁的理论塑性区分布

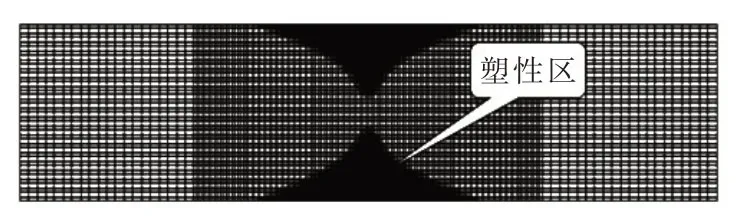
图2 集中荷载作用下数值迭代不收敛的塑性区

分析其原因，可能是由于式（14）是针对全区域的迭代，很难保证应力过于集中的局部小范围屈服函数得到精确满足。为了使屈服应力回归到屈服面，改善的收敛性，下面将在迭代式（13）中增加了应力在屈服点的回映迭代，即回映算法。

回映算法实质上是一种弹性预测和塑性修正过程，需要局部迭代调整塑性因子，使预测应力返回到屈服面[16]。这里的回映迭代式采用了半隐式向后欧拉方法[17]，其具体步骤如下所述。

（1）步骤1。给定n+1步的初始条件：计算令

图3 周围受压的圆形隧筒的塑性区

3.3 弹塑性全隐式迭代法的验证算例1。在隧洞开挖时岩体伴随应力重分布，隧洞周边局部可能进入塑性状态，其受力变形状态可以等同于厚壁圆筒，外部受均匀压力，如图3（a）所示。在围压p作用下，如岩体满足Mohr-Coulomb 准则屈服条件，隧洞半径为R0的圆孔周围塑性区半径具有理论解：其中，c为岩体的黏聚强度，φ为岩体的内摩擦角。本算例中，圆形孔口半径R0为1 m，若黏聚强度c取1.0 MPa，摩擦系数f即tanφ取0.2。按弹塑性全隐式迭代法采用两种方案求解，即分别采用和不采用局部回映迭代，计算得到图3（b）所示的塑性半径与压力关系曲线。由该曲线可以看出，施加外部周边压力至6.5 MPa之前，两种方案得到的塑性半径与压力关系曲线，与理论曲线基本一致。但在压力值大于6.5 MPa 之后，采用局部回映迭代的数值解与理论解仍然吻合较好。图3（c）给出了在外部周边压力达到7.0 MPa时，采用局部回映迭代得到的塑性区分布情况，此时塑性半径Rp为3.0 m，与理论值基本一致。

算例2。仍以如图1所示的简支梁为例，设梁材料的弹性模量取1GPa，泊松比取0.25，并为理想弹塑性材料，服从Mises 屈服准则，屈服应力σs取2.7 MPa。在上、下边缘正应力刚达到屈服，此时的荷载定义为Ps，即有令b=1 m，h=0.1 m，l=0.6 m，则

用0.1Ps增量荷载进行静态数值模拟，加载至1.5Ps，即MpMe =1.5时，计算得到塑性区分布如图4所示。与如图1所示的理论塑性区分布相比，此时计算得到的塑性区分布与理论塑性区分布几乎完全相同。与图2的计算结果相比可以看出，采用局部回应迭代后使迭代收敛性得到了大大的改善。

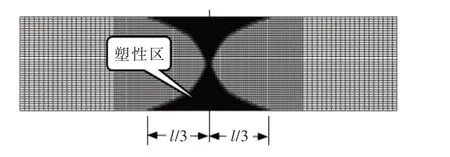
图4 集中荷载作用下的塑性区数值模拟

以上数值计算是在配置为Intel Core i5-2400 CPU@3.10GHz，MEM 2.99GB 的PC 机上进行的。在上面的算例中，平衡迭代误差屈服函数控制在简支梁有限元数值模型共有13 202个自由度，15个加载步，耗时不到3 min；平衡迭代最多需要15次迭代；局部迭代只需3或4次即可趋近于零。这说明本文提出的迭代法具有较高的计算效率，并且迭代稳定性良好。

4 弹塑性损伤问题的全隐式迭代法

4.1 求解弹塑性损伤方程的隐式迭代式在有效应力空间中，有效应力取代实际（名义）应力σ。按照应变等效假设，在实际物理空间里的实际应力σ可用损伤参数d和有效应力表示为混凝土非线性变形的分解，及其与弹性塑性损伤的关系如图5所示，E0为初始弹性模量，为极限弹性强度，ε0为与极限弹性强度对应的极限应变，即有为塑性应变（残余应变），εel为弹性应变。由于有效应力随弹塑性应变的增加而单调增加，因此屈服面总是膨胀状态，因此，实际物理空间里的材料变形软化不会导致有效应力空间的屈服面收缩。

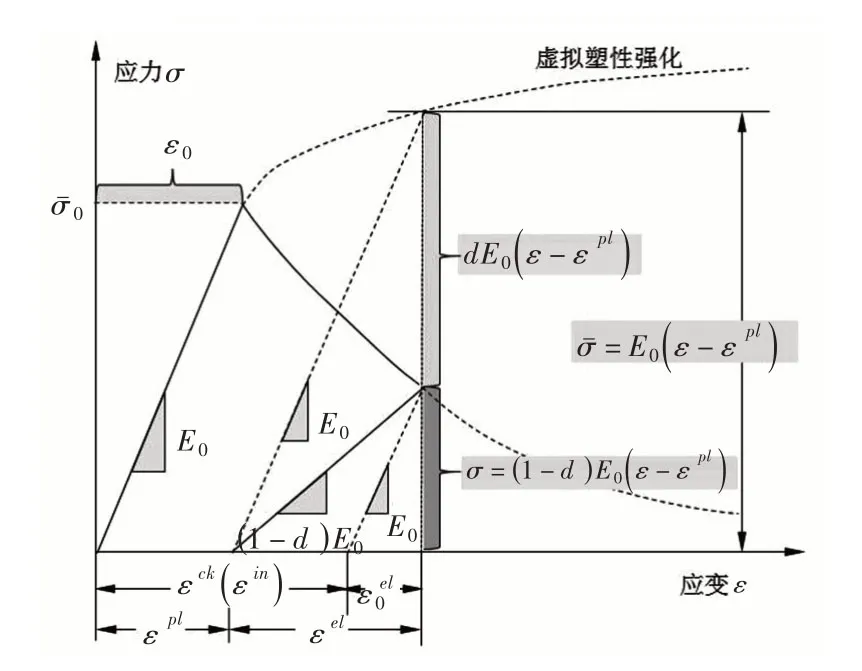
图5 混凝土非线性变形与弹性塑性损伤的关系

由于有效应力σˉ和塑性变形满足塑性理论的屈服准则、强化法则、加载-卸载准则和流动准则，因此，第3节的弹塑性问题的全隐式迭代法可以移植到有效应力空间。在每一加载步内，保持外部荷载Fn+1为常量，在第k迭代步的迭代式（14）可以改写为如下求解弹塑性损伤方程问题的隐式迭代式：

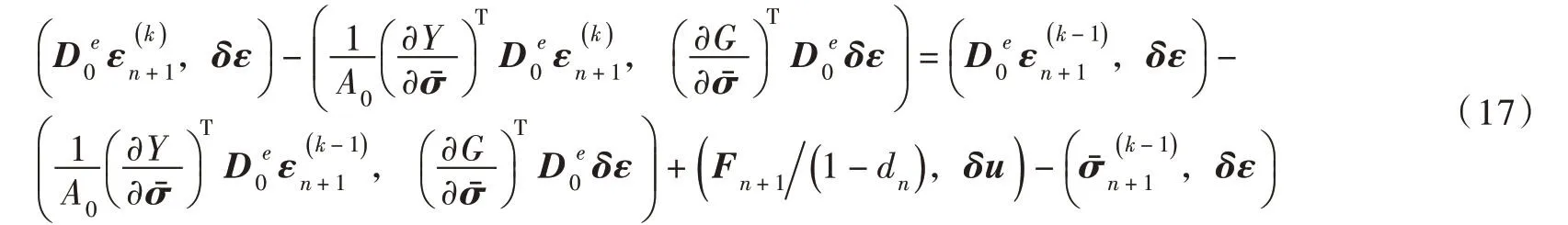
另外，式（17）的迭代式是以全量的形式给出，这样应用该方法分析高坝地震响应时，可以方便地以全量的形式输入地震动荷载。

4.2 弹塑性损伤全隐式迭代法的验证屈服准则采用Lee和Fenves[18-19]基于Lubliner 等[20]提出的混凝土塑性损伤模型，塑性流动势函数采用Drucker-Prager 双曲线函数。计算模型采用混凝土试件尺寸和网格剖分如图6。取文献[21]的轴拉试验和轴压试验观测数据：弹性模量为53.6 GPa，抗拉强度为1.84 MPa，抗压强度为25.28 MPa，泊松比为0.2，密度为2400 kg/m3。由文献[22-23]试验观测数据分析得到如图7和图8给出的混凝土材料的峰（失效）后应力、损伤变量与非线性（开裂）变形关系曲线。

图6 混凝土试件有限元数值模型及网格剖分（单位：mm）

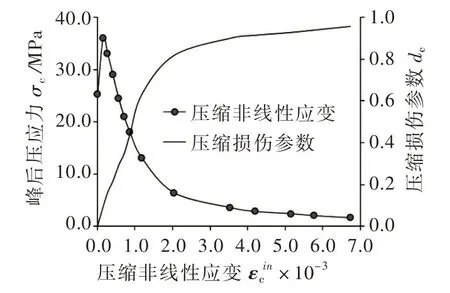
图7 压缩非线性参数曲线

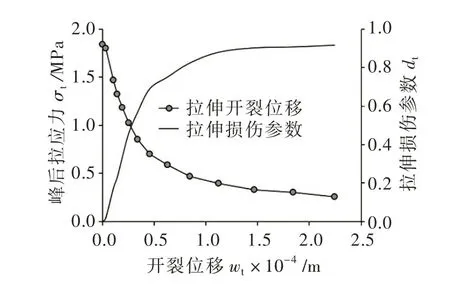
图8 拉伸非线性参数曲线

为了保证在跨中区域发生断裂破坏，将梁跨中下边缘宽45 mm×高22.5 mm 的区域的弹性模量分别取0.67 GPa和5.36 GPa，即为实测弹性模量的1/80和1/10。对图6所示的混凝土弯拉试件，施加竖向位移荷载P（w），位移增量取为10-3mm，进行弯拉破坏全曲线数值模拟。为了消除计算结果的网格敏感性，在有限元计算时，由图8给出的损伤变量和峰后应力与开裂位移关系，计算单元拉伸塑性应变单元的特征长度he取单元面积的平方根。

图9给出了随竖向位移增加，梁的弯拉应力由弹性阶段到达峰值，然后进入软化阶段的过程。梁（P为荷载，L支座间距，b为梁厚度，h为梁高度）与梁上边缘中点竖向位移相对应。

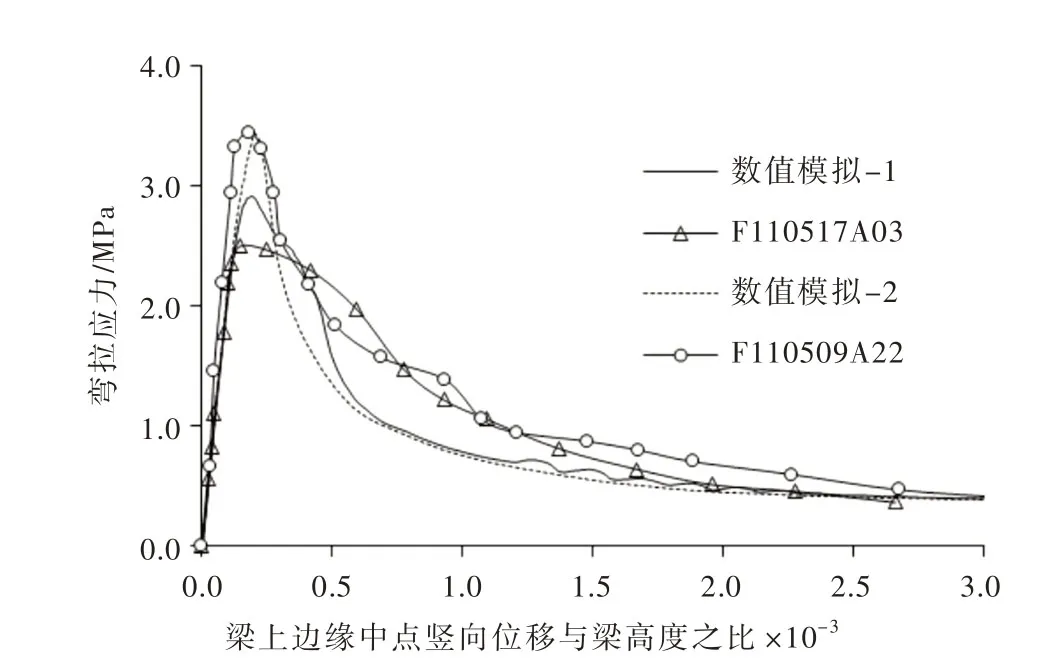
图9 混凝土试件弯拉应力与变形全曲线数值计算与试验结果

表1 混凝土静态弯曲破坏试验值与计算值

表1列出了由同一批次混凝土浇筑两个混凝土试件[21]：编号为F110509A22和F110517A03 弯拉峰值上边缘中点弯拉应力荷载及其对应的弯拉强度的试验值和数值计算结果，其中数值模拟-1计算得到弯拉应力峰值为2.90 MPa，与试件F110517A03 试验值2.49 MPa 比较接近；数值模拟-2 计算得应力峰值为3.40 MPa，与试件F110509A22的试验值3.45 MPa接近。

由图9给出的混凝土试件弯拉应力与变形全曲线中的数值计算与试验结果对比可以看出，在软化曲线的中间段，数值模拟与试验观测曲线存在一定差异，但最后与实测试件的软化变形曲线趋于一致。另一方面，从梁跨中局部区域弹性模量不同取值所得两条计算全曲线分别与同一批次混凝土两试件的试验结果相吻合，这也说明实际试件在局部材料性能的不均匀可能是导致试验观测结果差异的诱因。

图10给出了试件弯拉损伤破坏数值模拟结果。图10（a）为加载至荷载峰值状态下的最大主应力分布，最大主拉应力接近抗拉极限强度1.84 MPa，位于裂纹的扩展的前沿，说明最大应力控制在屈服面上；图10（b）给出的损伤云图是梁弯曲变形接近失稳时的损伤云图，由图10（b）看出，梁从跨中下边缘开始起裂，向上边缘扩展。由以上混凝土试件弯拉损伤破坏全过程的数值模拟分析可以看出，计算结果与材料试验观测结果吻合较好，从而验证了本文提出的弹塑性损伤问题的隐式迭代法的正确性。

图10 混凝土试件弯拉损伤破坏数值模拟结果

5 结论

本文的全隐式迭代法将屈服函数和塑性流动方程作为基本方程，联立隐式求解由平衡方程、屈服条件和塑性流动方程组成的方程组，无需显式计算弹塑性矩阵。该算法在引入局部回映迭代法后，通过很少几次回映迭代就可以获得理想的收敛精度，并且具有很好的数值稳定性。

由于在有效应力空间里混凝土类材料的塑性损伤遵循塑性变形规律，本文基于等效应变假设，将混凝土类材料的弹塑性损伤问题分解为弹塑性问题和损伤问题。应用弹塑损伤问题全隐式迭代法在有效应力（虚拟）空间计算塑性变形，再按应变等价的原则，考虑材料的损伤程度，即借助于损伤参数将有效应力转换为物理空间的实际应力。本文混凝土试件弯拉损伤数值计算表明，在有效应力空间里，随有效应力的增加，塑性（残余变形）屈服面处于膨胀状态，混凝土弹塑性损伤问题的全隐式迭代是稳定的。由于损伤参数为塑性应变的单调增函数，因此损伤参数的增大只会影响实际应力的大小，而不会影响塑性变形迭代求解的稳定性。

最后强调指出，本文的隐式迭代格式是以全量的形式给出，这样应用该方法分析高混凝土坝非线性地震响应时可以很方便地以全量形式实现地震动荷载输入。另外，本文提出的弹塑性损伤问题全隐式迭代法不仅适应于混凝土坝体，也适应于坝基岩体的弹塑性损伤问题的求解。