混凝土坝健康状态态势诊断方法
2020-11-19朱延涛顾冲时黄潇霏曹文翰
顾 昊,朱延涛,顾冲时,黄潇霏,曹文翰
(1.河海大学 农业科学与工程学院,江苏 南京 210098;2.河海大学 水利水电学院,江苏 南京 210098;3.河海大学 图书馆,江苏 南京 210098)
1 研究背景
混凝土坝健康状态诊断本质上是一个多层次、多指标且具有不确定性的复杂问题。由于表征混凝土坝健康状态的监测效应量随影响因素等变化而变化,因此对于日常混凝土坝安全管理而言,需要了解混凝土坝在复杂多变影响因素等作用下健康状态,而且混凝土坝健康状态是否有恶化,可通过表征混凝土坝健康状态的各类监测效应量的变化规律来进行诊断[1-3]。
诊断技术是把握大坝健康状态的研究重点。学者们目前主要基于模糊数学[4-6]方法对大坝健康状态进行综合诊断,其诊断技术包括模糊聚类分析、模糊模式识别和模糊综合评判等。吴中如等[7]综合模式识别与模糊评判法,构建了大坝安全综合评判体系,并将理论成果应用于实际工程。马福恒等[8]综合模糊控制理论和专家经验,以模糊综合评判法为基础,提出了确定复杂结构混凝土坝结构性态诊断的模糊可靠度方法。李婷婷[9]综合粗集理论、神经网络和模糊数学等理论方法,构建了基于粗糙集的模糊神经网络混凝土坝健康状态诊断方法。田振华等[10]利用模糊综合评判模型,提出了确定诊断指标权重隶属度及被诊断对象等级层次的方法,解决了混凝土坝健康诊断指标体系构建模糊性问题。
随着信息技术及现代数学方法的不断发展,一些具有智能化及信息化特性的方法,如灰色理论、随机森林理论、混沌模型理论、云模型理论等,为大坝健康状态综合诊断提供了理论依据[11]。吴云芳等[12]依据灰关联理论,构建了混凝土坝服役性态的多级灰关联评估法,据此对混凝土坝健康状态进行综合诊断。何金平等[13]基于云滴特性,利用正向与逆向云发射器产生“综合云”,提出了基于改进云模型的混凝土坝健康状态诊断模型。
由于混凝土坝健康状态监测信息组成的多样性,各类监测效应量所表征的混凝土坝健康状态侧重不同,如变形监测信息宏观反映了混凝土坝结构变化方面的健康状态,而渗流监测信息则主要反映混凝土坝防渗能力的健康状态。目前常用的方法是通过拟定监测效应量的诊断指标来解决混凝土坝健康诊断问题[14-15],但在指标拟定过程中,存在指标融合过程物理意义不明确问题,影响了混凝土坝健康状态诊断的准确性。针对上述问题,本文提出态势诊断方法来对混凝土坝健康状态进行诊断。
2 混凝土坝健康状态态势诊断法的基本原理
混凝土坝健康状态态势诊断法诊断的核心思想是:基于对历史原位监测资料分析,构建混凝土坝状态转异面板数据分析模型,据此对混凝土坝健康状态可能恶化部位及时刻进行分析,并找到对应环境量下的影响因素工况,从而确定不利工况;并通过建立环境量空间向量对应关系,利用最大熵原理确定健康状态的阈值,无需指标融合拟定,即可实现对混凝土坝健康状态的诊断。
2.1 不利工况确定利用态势诊断法诊断混凝土坝健康状态变化趋势,需要确定表征混凝土坝健康状态的原位监测信息中历史上曾经出现过的不利工况,因此不利工况的选取则是首先需要解决的问题。混凝土坝服役过程中性能劣化达到一定程度后,有可能发生健康状态转异,而转异发生的时刻所对应的工况即为不利工况。为了有效地对混凝土坝健康状态转异进行识别,通常在混凝土坝中埋设大量的监测仪器对表征混凝土坝健康状态的效应量进行监测,效应量测值的变化客观反映了混凝土坝健康状态的变化,若效应量产生异常变化,则反映了混凝土坝健康状态可能发生转异。为了确定转异时刻及转异部位,本文基于原位监测资料,提出混凝土坝状态转异面板数据模型分析方法,据此确定混凝土坝健康状态转异时刻和不利工况。
混凝土坝状态转异面板数据模型,是指在一段时间内将表征大坝服役性态某类监测效应量的测值所构造的数据集合,也就是从时空变化维度,把某类监测效应量测值变化表征出来的模型[16-19]。若模型系数不稳定,在某个未知时刻,改换成另一种规律,这个时刻就是转异时刻,混凝土坝状态转异面板数据分析模型可表示为:

式中:I(t)为示性函数,当I(t <k0)时,示性函数I(t)为0,当I(t≥k0)时,示性函数I(t)为1;Dit为某类监测效应量测值;i为监测点个数;t为监测时间序列;N为空间维度;T为时间维度;xit、vit为影响因素向量,vit =Rxit,R为已知矩阵;β、β′为待估系数;wit为反映t时刻第i个测点特异效应和扰动影响的变量;αi为第i测点的特异效应变量(固定或随机);k0为转异点;γit为第i测点t时刻扰动量。
效应变量αi分成两大类,其中,在面板数据模型中,固定效应考虑了组内差异,可以得出一些个体变化差异的影响,而随机效应由于考虑了全部差异,从而可以对总体差异影响做出诊断。本文重点研究随机效应量的影响,为分析方便,将式(1)改写为矩阵形式,即:

式中:D为某类监测效应量测值矩阵;X、V为某测点t时刻的影响因素矩阵;β、β′为待估系数矩阵;w为反映各测点特异效应和扰动影响的变量矩阵;α为特异效应变量矩阵;γ为扰动量矩阵;L为eT和IN的Kronecker 乘积,eT为T维全一向量,IN为N维单位阵;假设xit与wit为独立同分布,w 的数学期望E(w)=0,ww′的数学期望
利用式(2)对混凝土坝健康状态进行诊断时,需利用hausman 法对效应量αi进行检验,若检验为有效,则可基于式(2)的混凝土坝状态转异面板数据模型对大坝健康状态转异时间和不利工况进行确定。由于式(2)中效应量是随机的,因此利用广义最小二乘法对式(2)混凝土坝健康状态任何可能的转异点k的参数进行估计,对应β、β′其参数估计的表达式为:

对应式(2)分析模型的残差平方和为:

则转异点的选取准则为:

式中:N′为转异点的位置;T′为转异时刻;为对应式(2)分析模型的残差平方和最小时转异点的位置和时刻,用′表示。
利用式(5)可确定混凝土坝健康状态转异时刻,并结合环境量监测资料找到对应转异时刻的影响因素工况,该工况即为不利工况。
以上讨论了辨识混凝土坝健康状态单转异点的情况,对于运行多年的混凝土坝工程,已遭遇到各种工况的考验,在表征大坝健康状态的长系列监测资料中,可能存在多个转异点,以下讨论混凝土坝健康状态多转异点辨识方法。
首先,利用式(1)—式(5)识别出第一个混凝土坝健康状态转异时刻k0,并以k0为间隔点,将监测时间系列t分为t1=1,2,…,k0-1和t2=k0+1,…,T两个时段,分别建立混凝土坝状态转异面板数据模型,并利用统计学检验判断模型系数是否稳定,若模型系数稳定则表示上述两个时段内不存在转异点;若模型系数不稳定,则表示对应建模时段还存在转异点,利用式(1)—式(5)识别出新的转异时刻k1,并以k1作为间隔点,将所在监测时间系列划分为两段,重复以上步骤,即可辨识监测时间系列t中存在的所有转异点。若划分后监测时间系列较短无法建模,则可根据专家经验辨识转异时刻。所有转异时刻对应的影响因素工况均为不利工况。
2.2 混凝土坝健康状态诊断上节利用面板数据模型分析方法确定了混凝土坝健康状态转异不利工况,在此基础上,下面研究利用态势诊断法对混凝土坝健康状态进行诊断的过程。
表征混凝土坝健康状态各类监测量的变化主要由影响因素变化引起,作用于混凝土坝的影响因素主要有上下游水压力、温变荷载、时效和降雨等,图1为混凝土坝健康状态监测主要项目分类示意图。
由图1可看出,在影响因素作用下,通过各测点和各类监测量变化来反映混凝土坝健康状态的变化,也就是可利用定量分析影响因素等监测量的变化来诊断混凝土坝的健康状态。
设m天内混凝土坝影响因素监测量集合为其 中xkq为第k天在第q个影响因素监测量属性下的属性值,q=1,2,…,p。令某类监测量出现不利工况时影响因素监测量为P为监测量类别数。假设任意一天的影响因素监测量属性值集合Wk为空间坐标内的一个点,与空间坐标原点构成空间向量则任意一天影响因素监测量向量在表征某类监测量不利工况下影响因素监测量向量上的投影为:
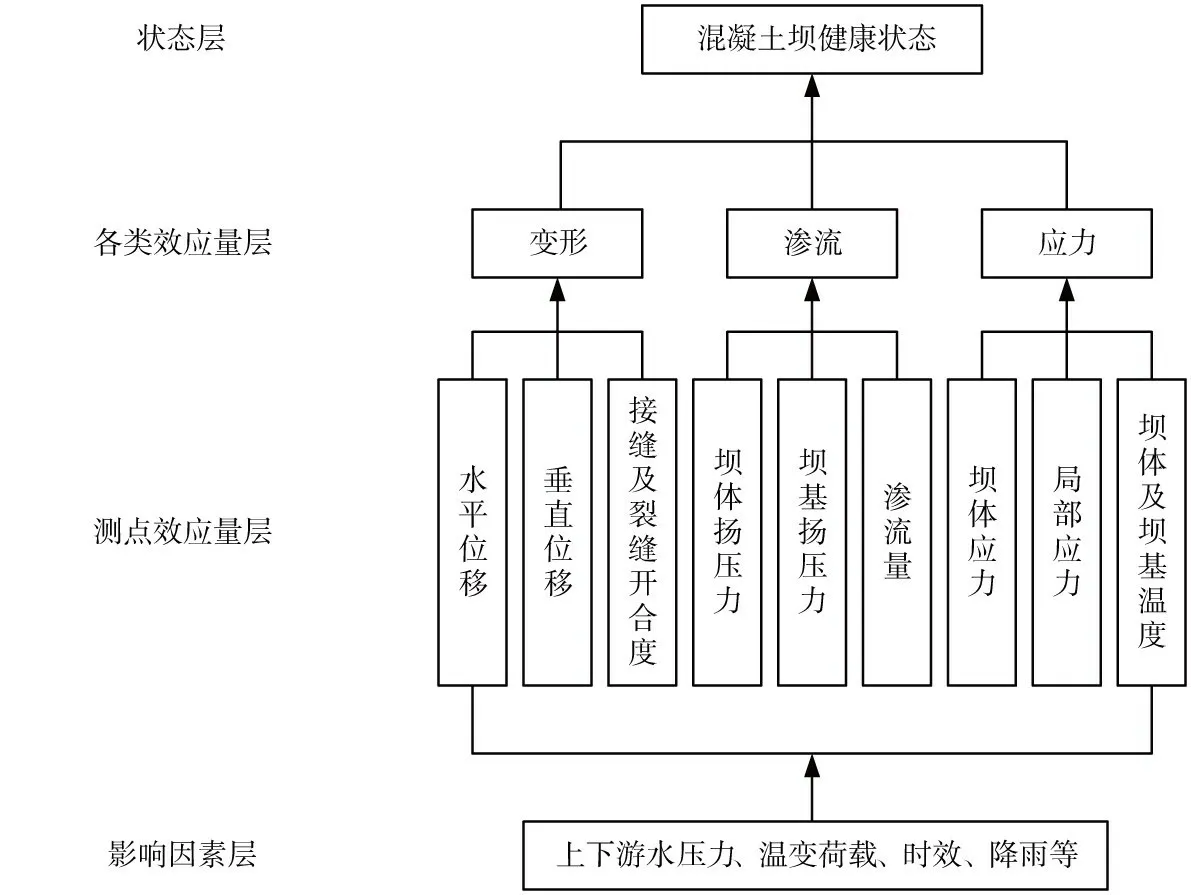
图1 混凝土坝健康状态监测主要项目

从几何形状上的相似程度而言,由式(6)可知,α(Wk)与β(W0l)影响因素监测量状态越接近,α(Wk)在β(W0l)上的投影值与β(W0l)的模就越接近,反之则差距越大。因此,本文基于灰色投影关联度理论[20-22],考虑用两者的差来表征任意一天影响因素监测量与不利工况当天影响因素监测量之间的关联程度,令:
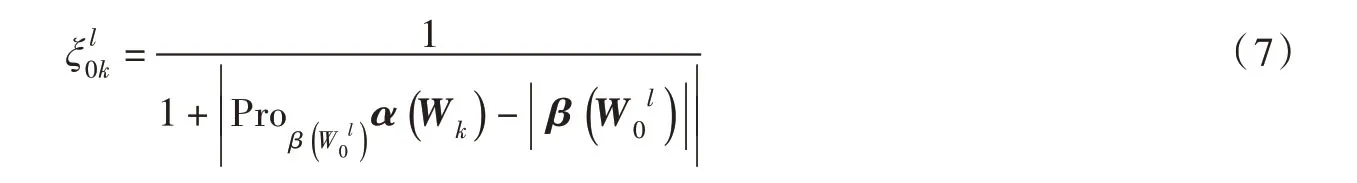
式中:为α(Wk)在β(W0l)灰色投影关联系数。
设ξ0k为α(Wk)在β(W0l)灰色投影关联度,则其表达式为:

由式(8)可知,ξ0k值越大,则说明此时影响因素监测量状态与不利工况下影响因素监测量状态越相似,若超过某一阈值ξm时,表明混凝土坝健康状态可能产生恶化,下面研究确定阈值ξm的方法。
2.3 混凝土坝健康状态态势诊断阈值ξm确定 本文利用最大熵原理来确定态势诊断阈值ξm,最大熵理论无需提前假定随机量的分布概型,只要根据较少的变量统计信息得到的数字特征值进行估计,就能获得精度较高的概率密度函数[23-25],适合混凝土坝原位监测信息不利工况灰色投影关联度概率密度求解,下面研究态势诊断阈值ξm的具体确定方法。
对于表征混凝土坝健康状态变化灰色投影关联度连续型变量ξ的信息熵定义为:

式中:为ξ的分布密度函数。
根据最大熵原理可知,最客观的概率密度分布是在满足根据已知样本统计信息所获得的一些约束条件下使熵达到最大值的分布,即:
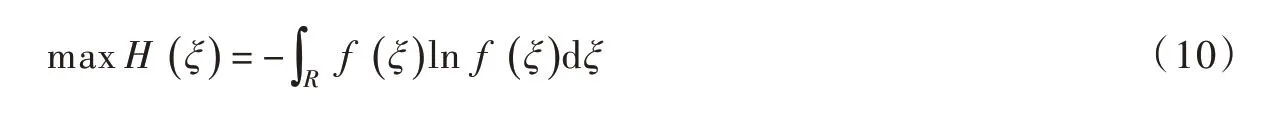
式(10)的约束条件为:
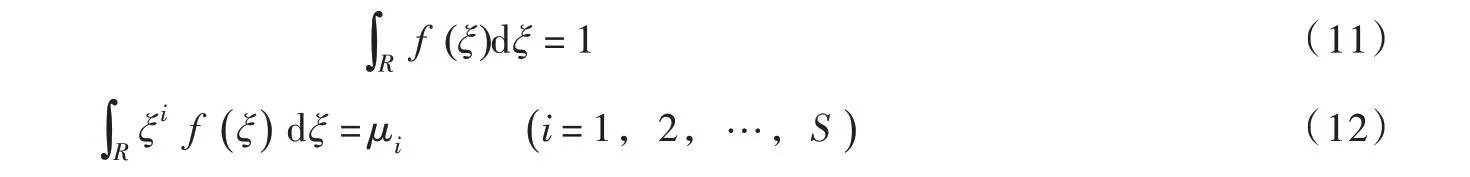
式中:R为积分空间;μi为第i阶原点矩;S为原点矩阶数。
利用伴随算法进行求解,首先建立相应的拉格朗日函数:
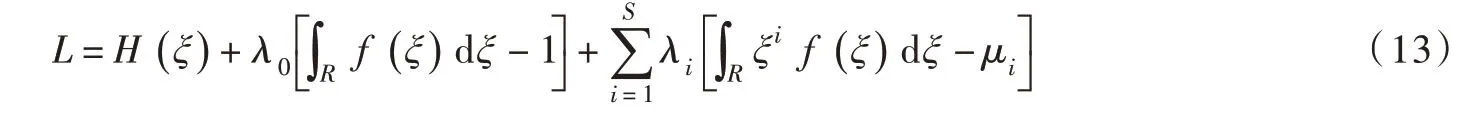

式中,最重要的就是伴随算子λi的确定,将式(14)代入式(11)、式(12)可得:
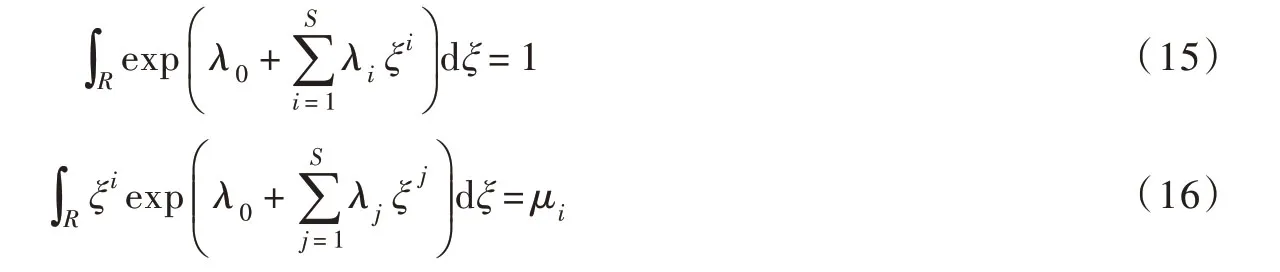
将已知表征混凝土坝健康状态变化的样本数据代入式(15)和式(16),求解伴随算子λi,并基于式(14),构建灰色投影关联度ξ最大熵概率密度函数f(ξ),在此基础上,根据大坝重要性选择置信水平α(1%~5%),则有:

由灰色投影关联度ξ最大熵概率密度函数以及给定的置信水平α,通过式(17)确定态势诊断阈值ξm,由此利用本文2.2节提出的方法来诊断混凝土坝健康状态。
3 工程实例
某大坝是一座同心圆变半径的混凝土重力拱坝,坝顶高程为126.3 m,最大坝高为76.3 m,坝顶弧长419.0 m,坝顶宽8.0 m,最大坝底宽53.5 m。自左向右有28个坝段,坝址地质条件复杂,由于在浇筑Ⅱ期混凝土时,层面上升速度较快,浇筑层间歇时间短,Ⅱ期混凝土收缩变形受到Ⅰ期混凝土强烈约束,导致在Ⅰ期混凝土顶部(105 m 高程附近)产生裂缝,自5#坝块一直延伸至28#坝块,长达300余米。经探测,裂缝深达5 m 以上,削弱了坝体刚度,对坝体整体性产生了较大影响。为了监控该工程的安全,在大坝上布置大量的安全监控仪器,其测点分布如图2所示,选取时间序列为1973年1月1日至2000年12月31日及2001年1月1日至2013年10月30日的实测变形垂线测点资料,对该坝健康状态进行诊断。
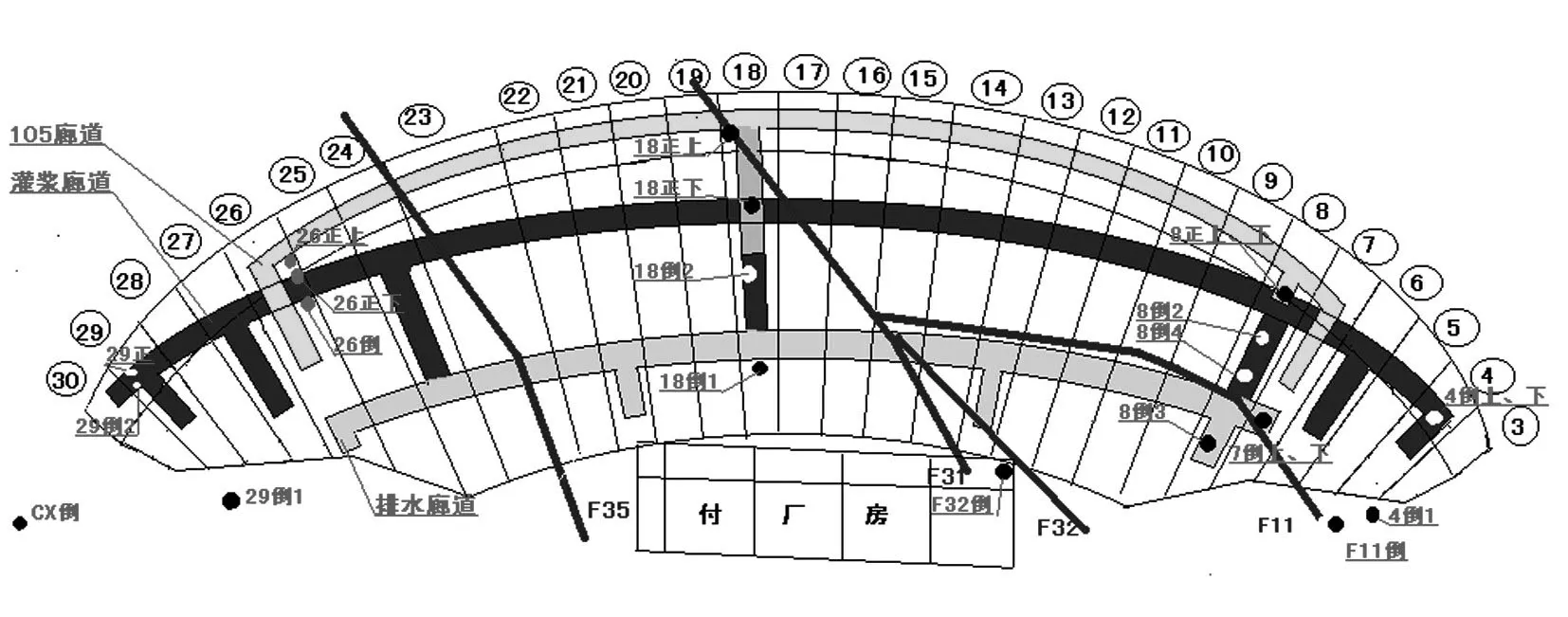
图2 某混凝土坝测点布置
利用态势诊断法诊断该混凝土坝健康状态变化趋势,首先要确定该坝健康状态原位监测信息中历史上曾经出现过的不利工况对应的环境量,本文选取时间序列为1973年1月1日至2000年12月31日的实测变形垂线测点资料,垂线测点分别为4倒1、4倒2上、4倒2下、7倒上、7倒下、8正上、8正下、8倒2、8倒3、8倒4、18正上、18正下、18倒1、18倒2、26正上、26正下、26倒1、29倒1、29 正1和29倒2。利用该坝变形监测资料通过式(1)建立状态转异面板数据模型,模型中考虑的主要影响混凝土坝某一时刻t任意一点i变形Dit的因素有水压、温度、时效。其中:水压影响因子有温度影响因子有时效影响因子有θt、lnθt,详见表1和表2。
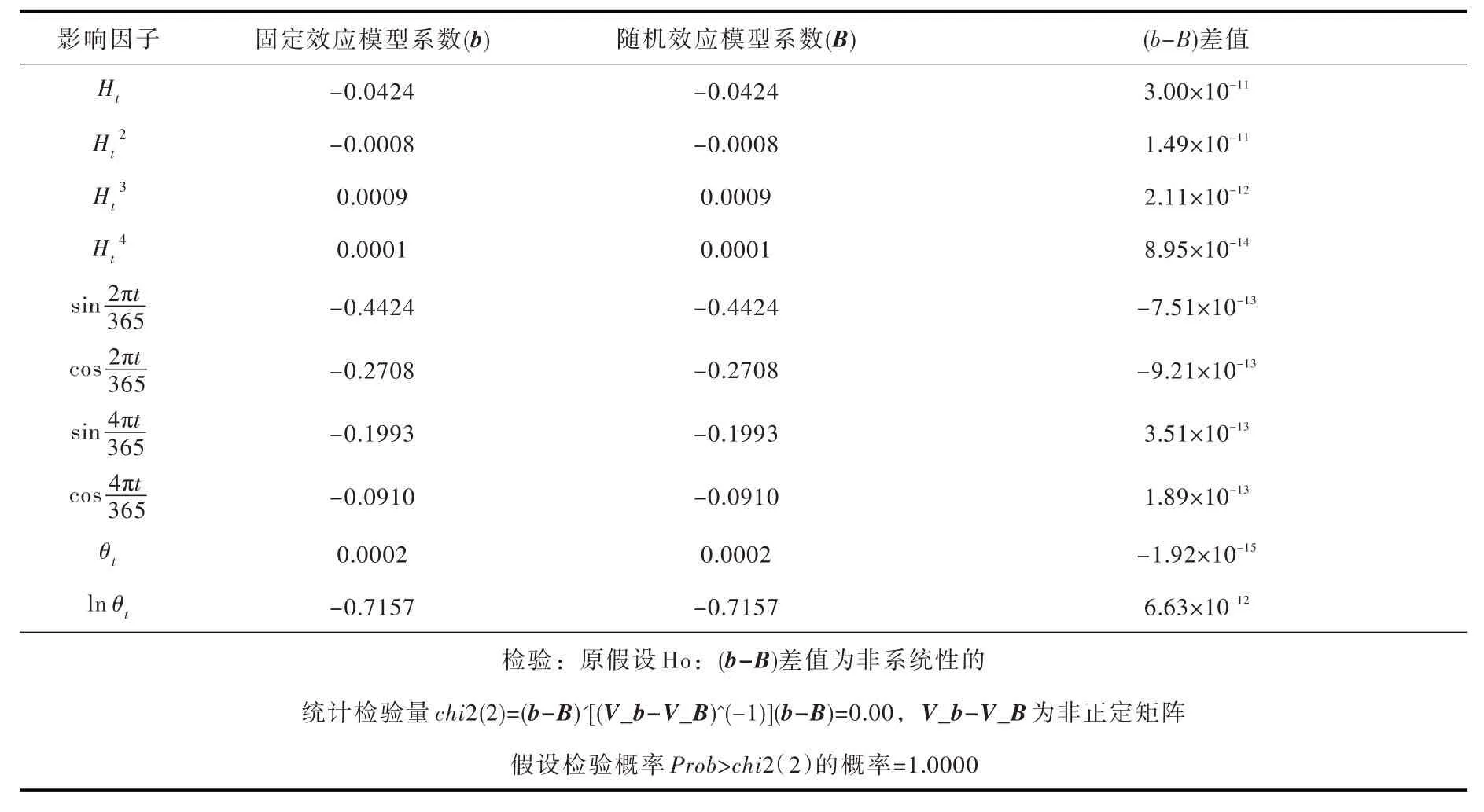
表1 Hausman检验
利用Hausman检验法,检验通过式(1)建立的状态转异面板数据模型是否可以利用随机效应面板数据模型进行建模,Hausman检验如表1所示,表中系数b、B 全文均保留4位小数。
经检验,固定效应模型系数(b)与随机效应模型系数(B)的差值为系统性的,因此,所选取的监测数据可以利用随机效应面板数据模型进行建模,则利用广义最小二乘法建立的随机效应面板数据模型,所建立的模型如表2所示。
由表2可看出,所建立的模型精度较高,可利用建立的面板数据模型对混凝土坝健康状态转异进行识别,经判断所建立的面板数据模型并不稳定,即系数β在某些时刻发生了变化,表明该坝健康状态在建模时段有转异发生,利用式(1)—式(5)对转异时刻进行辨识,假设测点资料时间序列第一天1973年1月1日为混凝土坝健康状态转异时刻k0,计算分析模型的残差平方和,接着假设1973年1月1日后下一次监测时刻为转异时刻,计算分析模型的残差平方和,以此类推,直到该测点资料时间序列的最后一天2000年12月31日,比较所有残差平方和大小,残差平方和最小的时刻为1977年4月7日,即该混凝土坝健康状态第一个转异时刻为1977年4月7日,将该时刻作为间隔点,将测点资料时间系列划分为t1=1973年1月1日,…,1977年4月6日和t2=1977年4月8日,…,2000年12月31日,分别建立混凝土坝状态转异面板数据模型,判断模型系数均为稳定,表明t1和t2段不存在转异点,因此该混凝土坝健康状态转异时刻为1977年4月7日。由该混凝土坝监测资料分析报告[26]可知,该混凝土坝于1976年至1977年间,经历了高温低水位和低温低水位的过程,连续出现不利影响因素组合致使该混凝土坝产生较大变形,且下游面105 m 高程裂缝发生了扩展(1977年4月以后,裂缝开度普遍增大),由此将该时刻选取为该混凝土坝监测资料不利工况,查找1977年4月7日监测资料中的环境量,即为不利工况环境量。下面利用态势诊断法对该混凝土坝健康状态进行诊断。
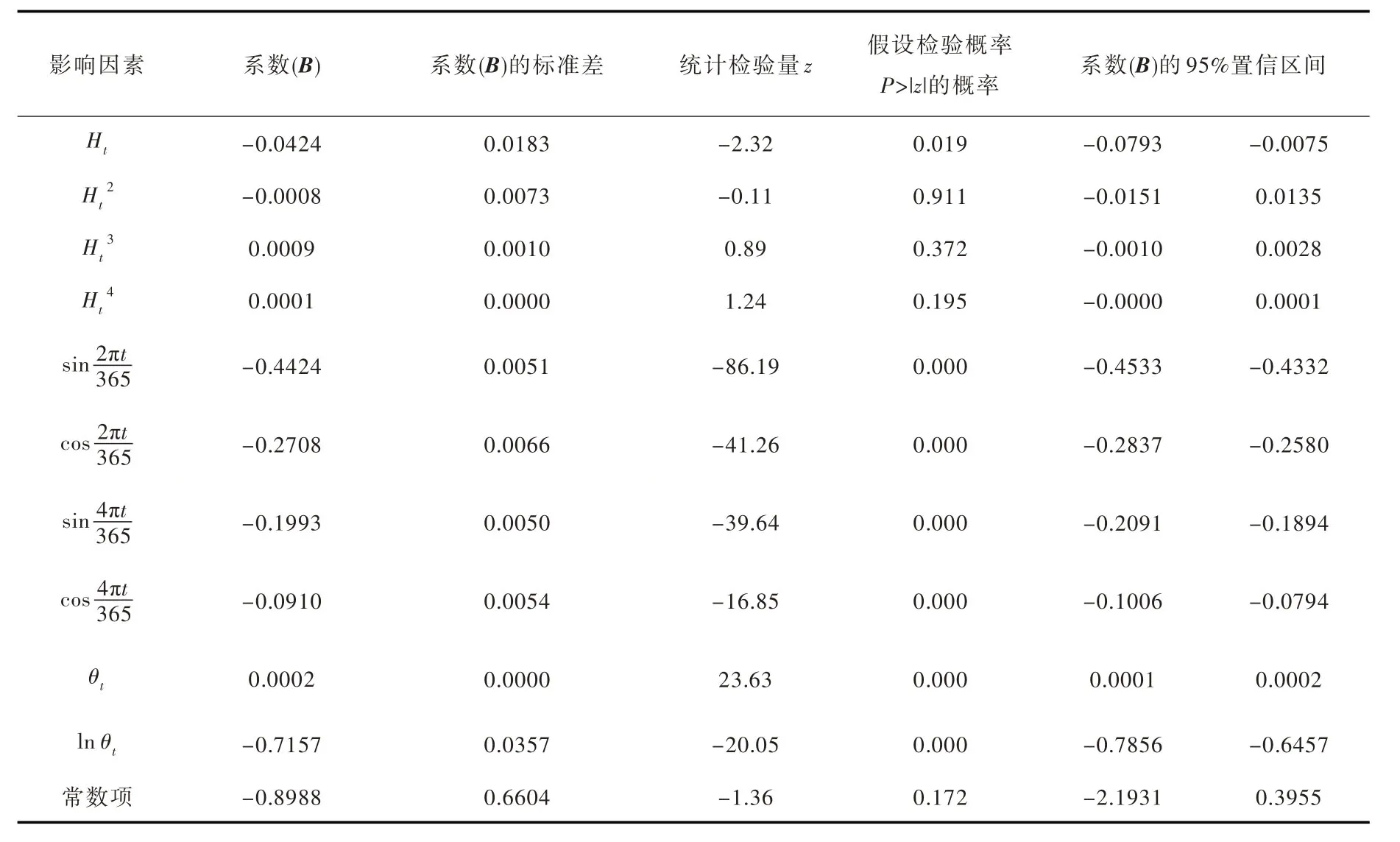
表2 某混凝土坝变形面板数据随机效应模型
将该混凝土坝1973年1月1日至2000年12月31日的水压、温变荷载以及降雨等环境监测量作为学习样本,利用式(6)—式(8)计算每日影响因素监测量与不利工况下影响因素监测量之间的灰色投影关联度,选取不利工况前后该时间序列灰色投影关联度值部分成果见表3。
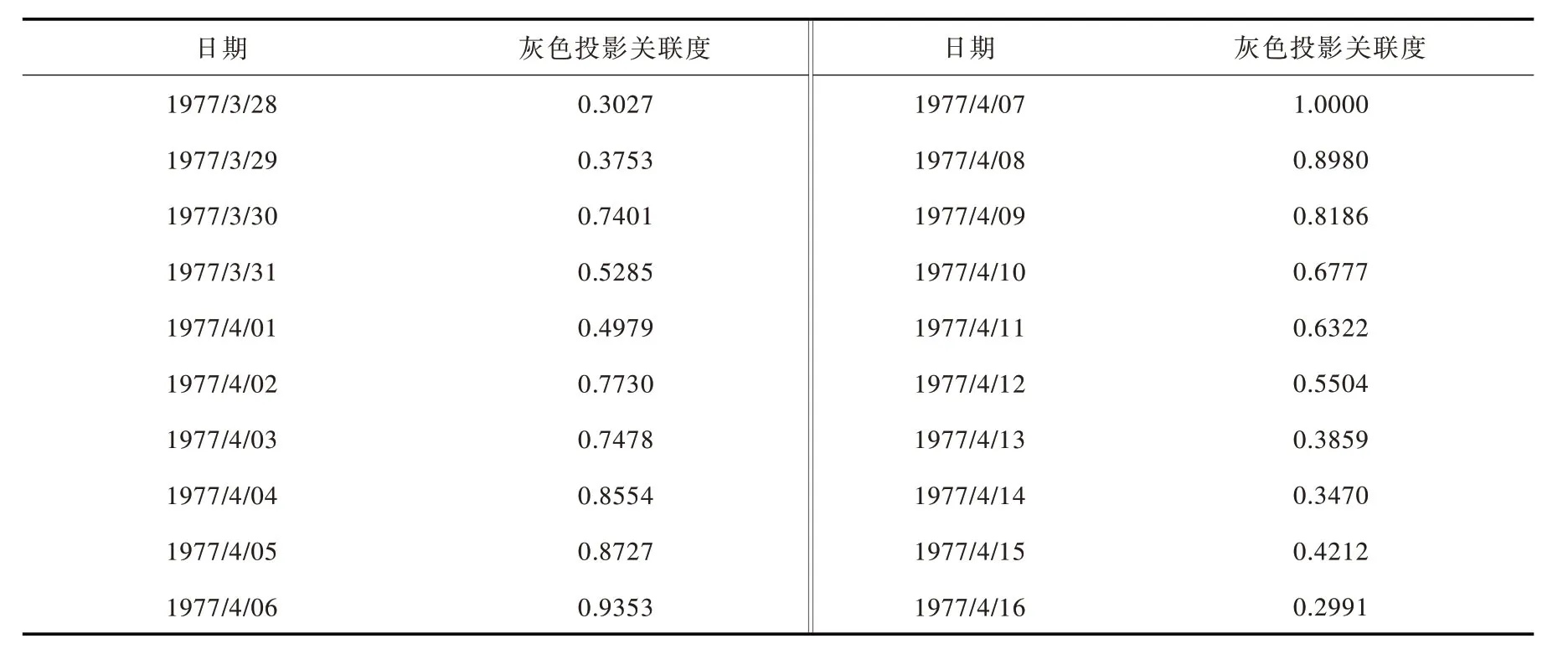
表3 1973年1月1日至2000年12月31日灰色投影关联度部分成果

表4 2001年1月1日至2013年10月30日灰色投影关联度部分成果
为了进一步诊断该混凝土坝健康状态,利用最大熵原理基于计算得的1973年1月1日至2000年12月31日的灰色投影关联度,根据该大坝重要性选择置信水平α为5%,利用式(17)求得态势诊断阈值ξm为0.935。接着选取监测资料样本2001年1月1日至2013年10月30日作为诊断样本,重复上述步骤,以1977年4月7日那天监测资料中的环境量作为不利工况环境量,计算每日影响因素监测量与不利工况下影响因素监测量之间的灰色投影关联度,并在其中找出超过态势诊断阈值ξm的日期,通过计算找出最早超过态势诊断阈值ξm的日期为2008年5月19日,见表4。
由该混凝土坝原位监测资料分析报告可知,对应2008年5月19日该坝健康状态主要影响因素与1977年4月7日相似,再加上2008年5月12日汶川8.0级强震对该坝扬压力孔水位产生了一定的影响,地震引起的地应力改变,致使扬压力孔水位快速升降变化,造成该坝变形较大且下游面2008年5月后裂缝开度平均值也较大,由此可能导致该混凝土坝健康状态恶化。分析结果与该混凝土坝的原位监测资料分析报告中的结论一致,从而证明了本文提出的混凝土坝健康状态态势诊断方法的有效性。
4 结论
本文利用提出的混凝土坝状态转异面板数据分析模型确定不利工况,在此基础上,研究并给出了态势诊断法诊断过程及健康状态变化阈值确定方法,利用提出的方法实现了对混凝土坝健康状态的诊断,得到如下结论:(1)基于对原位监测资料分析,构建了混凝土坝状态转异面板数据分析模型,利用该模型确定混凝土坝健康状态转异的部位及时刻,找到转异时刻对应的环境量,据此确定不利工况。(2)综合运用灰色关联理论,建立了环境量空间向量对应关系,并以目标向量与不利工况向量的距离为依据,表征了任意一天影响因素监测量与不利工况当天影响因素监测量之间的关联程度,构建了影响因素监测量与不利工况影响因素监测量间灰色投影关系,由此判别诊断时刻影响因素监测量状态与不利工况下影响因素监测量的相似程度。(3)基于最大熵理论,通过灰色投影关联度构建了最大熵概率密度函数,并在给定的置信水平下,提出了确定态势诊断阈值的方法,从而实现了对混凝土坝健康状态的诊断,并通过实例验证了所提出方法的可行性和有效性。
