苏教版高中数学新教材《阅读》栏目的教育功能挖掘

花奎

摘要：苏教版高中数学新教材（2019年版）与修订之前的旧教材相比，一个显著的变化是，新增了不少内容拓展或数学文化方面的阅读材料，并且将所有阅读材料统一放置于每一章后面新设的《阅读》栏目中。《阅读》栏目充分体现了教材的社会性、学科性与学习性。故教师应该充分发掘其国家意志，追求立德树人的效果;理解其学科意义，落实核心素养的培养;深入其学习过程，促进认知结构的完善。

关键词：数学教材 《阅读》栏目 教育功能

苏教版高中数学新教材（2019年版）与修订之前的旧教材相比，有诸多变化和亮点。其中一个显著的变化是，新增了不少内容拓展或数学文化方面的阅读材料，并且将所有阅读材料统一放置于每一章新设的《阅读》栏目中。显然，作为新教材的重要组成部分，《阅读》栏目的地位与作用不容忽视。通过研读，笔者发现，《阅读》栏目充分体现了教材的社会性、学科性与学习性，教师应该充分挖掘其教育功能与价值，实现育人目标。

一、发掘国家意志，追求立德树人的效果

《学记》开篇以“君子如欲化民成俗，其必由学乎！”明义，指出国家兴办教育是为了改良社会、易风化俗。教育作为一项国家事业，必然承担着促进社会发展与进行社会教化的基本功能。在2018年的全国教育大会上，习近平总书记再次强调，“坚持把立德树人作为根本任务”。作为教育的内容载体，教材必然要贯穿与突出立德树人的价值诉求与基本指向。对此，教师在教学中需要进一步发掘。

《阅读》栏目中的数学文化内容，蕴含丰富的人文情感和哲学道理，可以对学生进行德育。教师在教学中应该充分挖掘相关因素，采取恰当的方式进行渗透，从而实现立德树人的教育功能。

例如，必修第二册第11章《解三角形》中《阅读》栏目的文章《流星不是地球蒸发物》中写道：

仰望星空，时有流星划过天际。“流星，飞走天空，可能有一秒时的凝望，然而这一瞥的光明，已长久遗留在人的心怀里。”（引自冰心《繁星·春水》）人们赞美流星，是因为它燃烧着走完自己的全部路程。

……

我们知道，云层最高不超过15 km，所以可以断定流星不是地球蒸发物，它一定是天外来客！正是余弦定理和正弦定理帮助人们迈出正确认识流星的第一步！

这里，《繁星·春水》的引文让学生不仅感觉到流星是宇宙的奇迹，而且感受到“流星”的奉献和牺牲精神，激发了学生的崇敬之情。而且，利用余弦定理和正弦定理解决流星的高度問题，断定流星不是地球蒸发物，彰显了批判和求实的精神。

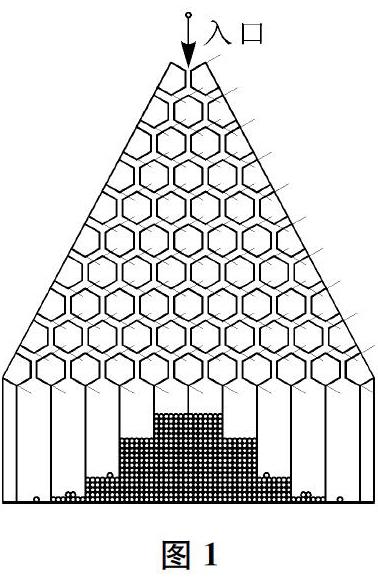
再如，必修第二册第15章《概率》中《阅读》栏目的文章《制作杨辉三角形》，其中写道：

制作一个如图1所示的通道及下方相互隔离的储槽。若把1粒球形小珠放入最上方的通道入口，则小珠落入下方每个储槽的概率有何规律？

……

图2所示的数表最早由我国宋朝时期的数学家杨辉于1261年画在他所著的《详解九章算法》中，并说明出于《释锁算书》，贾宪曾用过此图。西方称此图为帕斯卡三角形，是帕斯卡于1654年发表的。

教学中，可以融入杨辉三角形背后的数学文化，结合（a+b）n展开式中二项式系数的分析，遵循由特殊到一般的原则，引导学生从不同的角度认识蕴含在各个展开式二项式系数之间的关系。杨辉三角形背后的文化意蕴，能使学生油然生起对祖国历史文化的自豪，培养学生的爱国主义情怀。二项式系数规律的探究，能让学生体会到数学内容与形式的美，感受到数学的魅力——将求真和审美统一起来，既能提升学生的学习潜能，又能提高学生的审美情趣。

二、理解学科意义，落实核心素养的培养

教材具有学科性，必然蕴含着学科意义。作为教学内容的数学的学科意义是，以数学知识为基础、以数学理论为框架，指向“数学的实质”、数学核心素养，服务于学生的生存与发展。数学教育的根本宗旨是教会学生思考。《普通高中数学课程标准（2017年版）》提出，以核心素养为指导，其主要目的之一是促进学习方式的改变，引导学生学会学习，要加强“学法”指导。

《阅读》栏目中的很多内容也蕴含着丰富的数学研究路径和方法的指导，可以用来培育学生的数学核心素养。教师在教学中需要深度理解其学科意义，引导学生逐步学会用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界。

例如，必修第一册第2章《常用逻辑用语》中《阅读》栏目的文章《有趣的悖论》，介绍了两个有趣的悖论——芝诺的“阿基里斯追龟悖论”、罗素的“理发师悖论”。在学生刚学习高中数学不久，就介绍这两个数学史上著名的悖论，不可不说用意深远：奇趣且有一定难度的数学悖论可以充分引发学生的认知积极性，激发学生的探究欲望，让学生欲罢不能，从而在探究学习的过程中提升学生发现问题、提出问题、分析问题、解决问题的能力;数学悖论中蕴含的逻辑矛盾可以充分训练学生的演绎推理思维，让其体会数学的抽象性与严谨性。对于“阿基里斯追龟悖论”，学生很容易发现它与现实生活不符，但很难从逻辑上发现它到底错在哪里、推理的过程有什么问题;在对其的深入探究中，学生便会产生有限与无限思想（无限个量的和——无穷级数，可以是有限的大小）的萌芽，为后续极限与导数的学习埋下伏笔。对于“理发师悖论”，学生很容易通过修正理发师的规矩——将他自己排除在外来解决，自然而然地提出严格的“罗素悖论”又如何解决的问题，从而展开深入的探究学习，进一步提升自己的逻辑推理能力。

再如，必修第一册第6章《幂函数、指数函数和对数函数》中《阅读》栏目的文章《“怎样解题”表》，介绍了G.波利亚经典的“怎样解题表”。广义地看，数学解题（数学问题解决）就是数学研究的基本方式，从而应是数学学习的基本方式。“怎样解题表”将解题过程分成四个步骤，设置了大量的元认知提示语，集中体现了数学学科的基本思维方式以及理性探究精神，能够有效引导学生掌握数学思维，学会数学思考（研究和学习）。

三、深入学习过程，促进认知结构的完善

教材也是学材，具有学习性，必然蕴含着学习的过程——虽然有时只给出学习的引子。有意义的学习是一种深度学习，应该抓住知识的内核，触及心灵的深处，不断扩大知识间的联系，完善知识的结构。

《阅读》栏目中的很多内容是正文内容的拓展延伸，可以用来引导学生展开深度学习。教师要由此通过不断的追问，引导学生深入学习过程，探究相关知识的本质内涵、来龙去脉。

例如，必修第二册第10章《三角恒等变换》中《阅读》栏目的文章《弦表与托勒密定理》，介绍了托勒密推导两角差的正弦公式（用于制作弦表）时运用的托勒密定理。对此，教师可设计一系列探究活动，引导学生展开深度学习，揭示托勒密定理的内涵、价值和变化等，完善认知结构。笔者的教学设计如下：

1.情境引入。克罗狄斯·托勒密是古希腊著名的天文学家、地理学家、物理學家，一生著述甚多，其中《天文学大成》共13卷，《地理学指南》共8卷，引领西方科学上千年。他提供了人类历史上最早的有数学标识的地图投影法、经纬线、星历表。数学是天文学、地理学、物理学的工具性学科，托勒密的专业研究需要数学研究作为支撑。他的一个数学研究结论流传至今，即托勒密定理：圆的内接四边形的两组对边乘积之和等于两条对角线的乘积。

2.探究问题1：能用数学符号语言和图形语言表述托勒密定理吗？会证明吗？

引导学生用数学符号语言和图形语言表述托勒密定理，理解托勒密定理描述的是四点共圆长度方面的关系;引导学生多角度思考托勒密定理的证明方法（如三角形相似法、等面积变换法等），建立四点共圆与三点共圆的联系及长度关系与角度关系、面积关系等的联系。

3.探究问题2：为什么将托勒密定理放在《三角恒等变换》这一章中介绍？它与三角恒等变换知识有什么联系？

引导学生发现托勒密定理所表述的四点共圆长度方面的关系与两角和与差的正、余弦公式所表述的角度方面的关系，在结构上很相似（都是“ac+bd=ef”的形式），进而得到将三角函数看作直径为1的圆中角对应的弦长，利用托勒密定理证明两角和与差的正、余弦公式。这是数学史上关于三角函数的重要观点，由此便可进一步介绍弦表的由来。

4.探究问题3：托勒密定理还有哪些应用？

引导学生在从几何到三角的基础上，进一步从几何到代数（数形结合），发现托勒密定理在更广阔领域内的应用，感受托勒密定理的丰富价值。

5.探究问题4：托勒密定理可以推广和拓展吗？

引导学生通过探究认识到以下几点：（1）托勒密定理的一个退化结论是“若4个不同点A、B、C、D顺次在一条直线上，则也有AB·CD+AD·BC=AC·BD”;（2）托勒密定理的一个推广结论是“对于任意平面凸四边形ABCD，总有AB·CD+AD·BC≤AC·BD”;（3）托勒密定理是勾股定理和余弦定理的一般形式;（4）托勒密定理是多项式乘法法则的几何形式……

参考文献：

[1] 史宁中，王尚志.普通高中数学课程标准（2017年版）解读[M].北京：高等教育出版社，2018.

[2] 吴昊.利用托勒密定理巧解三角形[J].中学数学研究（华南师范大学版），2016（15）.

[3] 徐章韬，马菡，梁玉.对称性：从多边形到圆——教育数学研究之六[J].教育研究与评论（中学教育教学），2018（6）.

[4] 张小明.HPM视角下的教材理解与难点认识——以“两角差的余弦公式”为例[J].教育研究与评论（课堂观察），2015（8）.