小学生数学识图、画图与析图能力培养
2020-11-18蔡凤梅
蔡凤梅
摘 要 小学生数学识图、作图与析图能力的强弱直接影响到几何直观能力的发展,影响到学生数学素养的培养。因此,小学数学课堂上教师要致力于实现“多方法、多视角和多策略”,即多种方法培养学生数学识图能力、多种视角培养学生数学画图能力和多种策略发展学生的数学析图能力,从而有效提高学生识图、作图与析图能力,促进学生数学素养的发展。
关键词 小学生 数学 识图 作图 析图
基于几何直观主要是利用图形生动形象地描述数学现象、问题,有助于学生直观地分析问题,有效地架起数学抽象与学生思维直观之间的桥梁。因而在小学数学课堂上要关注学生识图、作图与析图能力的培养。纵观当下很多课堂,教师虽然能运用图形帮助学生理解数学知识,但更多的只是教师单向式的解析与引导,很少关注学生对图形的理解与运用。这显然不利于学生几何直观能力的发展,不利于学生可持续發展。笔者结合一些具体的教学案例谈谈如何培养学生识图、作图与析图能力,从而有效发展学生的数学素养。
一、多种方法,培养学生数学识图能力
教学实践表明,小学生容易对直观、生动的图形产生兴趣,并快速投入到学习活动中来。因此,我们要深入研究学生的认知特点和规律,并结合具体的数学知识,引导学生在识图活动中对图意进行有序的描述,培养学生从图中搜集、分析和处理信息的能力,体悟数学知识的产生过程,从而实现对数学知识的深度理解。
1.呈现多种图形位置,培养学生图形辨识能力
由于小学生生活经验和抽象思维能力有限,如果教师呈现的图形位置比较单一,则会导致学生窄化数学知识的内涵和外延。因而,教师要根据图形的本质特征,呈现丰富的图形素材进行多种图形位置的摆放,促使学生能在数学直觉的基础上正确了解数学知识的典型类型与常见变式,不断丰富数学表象,提高学生辨识图形的能力。
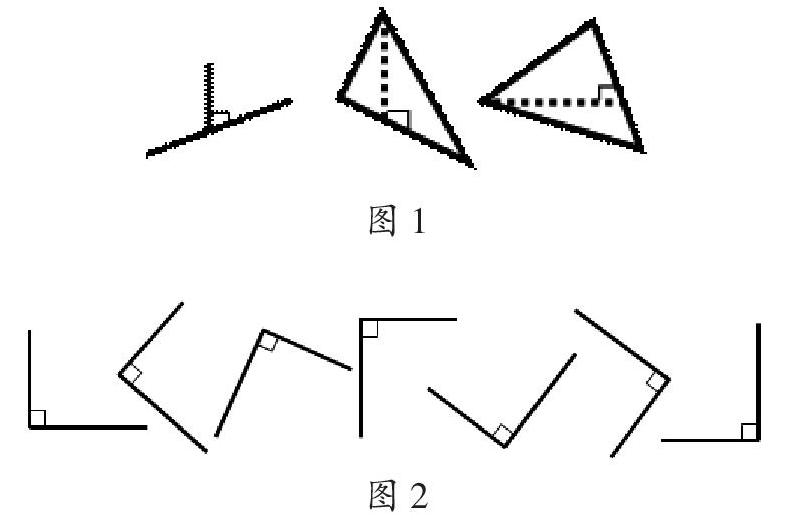
如笔者在教学人教版《数学》二年级上册“认识直角”一课时,让学生尝试用三角板画直角,发现大多数学生所画的直角都是由一条水平边与另一条竖直边组成的。显然学生对直角的认知并没有深入,只是想当然地认为直角就是由一条水平边与另一条竖直边组成的。如果对学生的这种“想当然”没有正确的引导,则直接影响到后续四年级画垂线与画三角形的高的学习(见图1)。因而,为了培养学生识图能力,笔者在黑板上呈现一组各种不同姿势的直角让学生辨别(见图2)。当学生初步对直角有一个建构时,笔者继续启发学生进行思考:为什么姿势不一样却都是直角?逼着学生通过观察、验证,从而领悟到直角不只是停留在文字层面的“直直的角”,而是只要两条射线所组成的角是90°,那么这个角就是直角。为了进一步让学生对直角有更深刻的辨识,笔者将班级里前桌的一位学生画的直角,正正地贴在黑板上,问大家是不是直角,继而多次、多角度地变换“贴”的方向,从而让学生发现同一个直角不管怎样摆放,终究还是直角。课堂上,通过多个直角图形位置的摆放让学生识别直角的真正内涵,又通过同一直角的不同摆放让学生识辨直角的外延,从而打破了学生的思维禁锢,建立概念清晰的表象,提升学生图形的识别能力,为后续学习打下了坚实的基础。
2.呈现多样图形变化,建立图形之间内在联系
“图形变换”是学生最常用于解决几何图形的重要数学策略。在数学课堂教学中,要灵活打通各种图形之间千丝万缕的内在联系,巧妙地运用平移、旋转、翻转、割补等方法来多样地呈现图形变化,从而增强学生的识图能力。如在教学人教版《数学》五年级上册“梯形的面积计算”一课时,可以引导学生将两个完全一样的梯形拼成一个平行四边形来推导面积计算公式,也可以启发学生将梯形进行割补,转化成一个平行四边形来推导面积计算公式,还可以通过画辅助线方法来推导梯形面积公式等等。同一图形不同变化推导出同样的面积计算公式,打通图形之间的内在联系,增强学生识图能力的同时,也有效地发展学生的数学思维。
3.呈现多维图形组合,提升图形综合识读水平
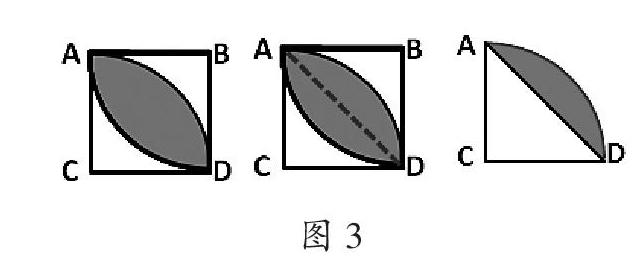
教师有意识地呈现复杂多维的图形组合,并引导学生从图中搜集、分析和处理信息,巧妙排除干扰因素,由表及里、去伪存真,抓住图形本质,激发学生利用“化繁为简”的数学思想方法巧妙地把复杂多维的图形转化成简单的图形,从而有效地提升学生的图形综合识读水平。如图3是边长为4cm的正方形,求阴影部分面积。这道题乍一看有点复杂,其中有正方形、扇形和三角形等多种图形,要求的是不规则图形的面积。在教学时,笔者引导学生连接AD,得到第二幅图,有的学生恍然大悟,得出阴影面积是以C为圆心与以B为圆心的两个90°的扇形交叉部分面积,但还是有部分学生表示不理解,于是笔者通过课件在第二幅图形上设计闪动动作抽象出第三幅图,这时学生的思路一下子清晰了。通过图形的分割与变换认识图形,成功将复杂的多维图形组合转化成简单熟悉的图形。经常性地进行这样训练,可以让学生从直观而复杂的图形中获取数学信息,并通过加工转化,激活数学思维,提升学生的综合读图水平。
二、多种视角,培养学生数学画图能力
用图形直观语言表述数学概念,可以有效降低数学知识的抽象程度,促使学生对数学本质有一个更为清晰的建构。因此,教师在数学课堂教学中要研透、读懂教材编排意图,充分挖掘教材资源,通过信息技术手段,将抽象的数学知识设计成直观图形,逐步培养学生借助几何直观进行思考的数学习惯。另一方面,利用图形可以有效地将复杂的数学问题变得简明、形象。因此在学生解决问题碰到困难时,要积极鼓励学生通过作图来寻找解决数学问题的途径。在培养学生数学作图能力的同时,激发学生的数学思维。
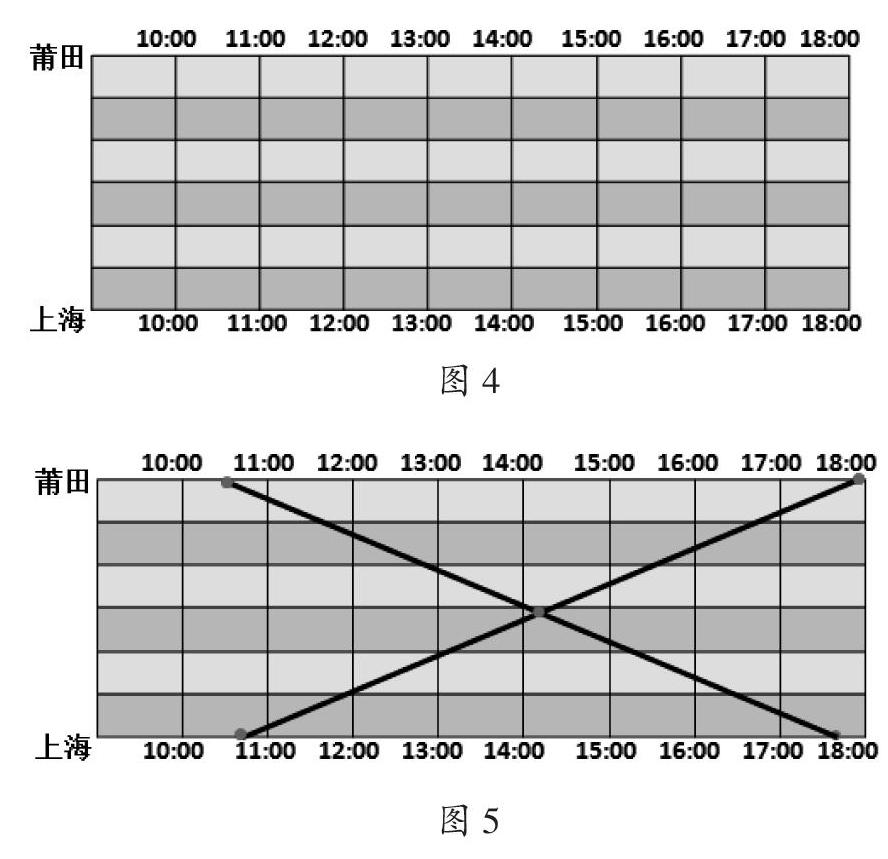
如在学习了“路程、速度与时间”一课后,笔者设计这样一道习题:“D3136次动车10:36从莆田站开出,17:42到达上海虹桥;D3135次动车10:41从上海虹桥开出,17:59到达莆田站。能知道这两列动车大约会在什么时间相遇吗?”这道题已知信息中没有两地之间的距离,只告诉起始站的发车时间与到站时间,如果只是运用常规思路(即“相遇时间=总路程÷速度和”这个数学关系式)来解决,显然是行不通的。在学生思维陷入困顿之际,笔者启发学生可以用数学作图的方法将题中的已知信息转化成图形,有的学生用画线段图的方法依然找不到出路。于是笔者继续启发,数学图形不只有线段图,一条线行不通,可以两条线,还可以是一个面。正当学生依然无解之际,笔者出示了坐标纸格图(见图4),学生瞬间顿悟,便马上动笔在自己的作业纸上画起来。不一会儿,学生都能通过画图找时间点,找到了问题解决的出路(见图5),从而得到两车大约会在14:15相遇。因而,画图是一种重要的解决问题的策略,借助图形的直观作用有效地降低了数学问题的难度。
三、多种策略,发展学生数学析图能力
借助图形进行数学思考、想象,从而进行合情推理使得问题得以解决,这一系列的过程大多需要引导学生理解数学文字语言,亲身经历动手画图,从而实现文字语言与图形语言的相互转换。然而,部分学生纵然在教师的引导下将数学文字语言转换成了图形语言,但对图形语言所要表达的数量关系仍然无法理解,这就需要我们关注学生的多种策略进行析图能力的培养。如果说识图是讓学生掌握辨识图形外在的数学直觉,析图则是让学生理解辨析图形所要表达的内在数量关系;如果说画图是学生将数学文字语言转换成了图形语言,析图则是将图形语言再次转换成了更为清晰、精炼的数学语言。
如笔者在教学人教版《数学》六年级上册“数学思考”这一节课时,出示“8个点可以连多少条线段”之后让学生动手尝试,由于学生在三年级时就有“比赛场次”“数线段”等学习经验,所以很快通过画图找到解决问题的方法,即7+6+5+4+3+2+1=28条。显然学生的思路是直接在一条直线上画出8个点,然后先数出每两点组成一条线段的有7条,继而是每两个间隔组成一条线段的有6条,再是每三个间隔组成线段的有5条……这种有序数线段的方法是之前学习经验的正迁移,符合学生的思维特征。而从教材的编写看(见图6),编者并非一下子给出8个点让学生来数,而是先给出2个点确定一条线段;再增加一个点,也就是再跟前面的这两点连接,所以增加了2条线段,即1+2=3;继而在3个点的基础上再增加1个点,而增加的1个点与前面的3个点连接又增加了3条线段,1+2+3=6;……从教材的编写意图出来,编者是要让学生发现“每增加一个点,增加的线段数其实就是前面点数的总和”。显然教材编者的用意是要让学生经历“画图”的动态过程,从而促使学生掌握n个点两两连线的规律,从而把握其中隐含的结构性数量关系。所以,笔者在学生展示自己的想法之后,便组织学生对教材所呈现的图形进行辨析,读懂教材每个图形背后所隐含的深意,寻找各个图形之间的前后联系。让学生结合算式析图,从而感受到图形的动态呈现,感悟在两点确定一条直线的基础上,每增加一点所增加的线段的条数则是前面点数之和,并发现图形变化后的规律。之后,让学生对自己画的图形与教材呈现的图形进行对比,从而发现:虽然数出的线段总数是一样,但其思维的过程是不一样的,前者是一种固定的模式,没有进行动态“画”的过程;而后者则是动态地呈现每增加一个点所产生的线段总和相应增加,不但展现动态的“画”的过程,而且动态地呈现数学内部结构,边画边数边发现其中的数量关系与规律。
综上所述,我们不但要增强学生的识图能力,使学生从直观的图形中获取数学信息,而且要提高学生的画图能力,让学生经历数学知识的抽象过程,致力于数学思维可视化,更要提升学生的析图能力,掌握文字语言与图形语言的相互转换,从而使数学素养的培养得以落实。
参考文献
[1] 侯美霞,李醒群.低年段解决问题教学中学生画图能力的培养[J].小学数学教育,2015(Z3).
[2] 杨志荣.浅谈画图法在小学数学解决问题教学中的作用[J].吉林教育,2015(20).
[责任编辑:陈国庆]
