初中数学常见开放题型初探
2020-11-18
用数学开放题培养学生的创新意识和能力,已成为教学的热点。重视开放性问题的教学,培养学生的探究习惯,提高学生探究能力、动手操作能力,是创新课堂提高教学质量的目标之一。现谈谈我对数学开放题的看法。
一、数学开放题的作用
素质教育的核心是培养创新精神和创造能力,数学开放题给学生进行创造性学习提供了宽松、自由的环境,它的作用有以下两个方面。
第一,数学开放题对学生的教育作用。学生必须打破原有的思维模式,展开联想和想象,从多角度、多方位、多层次进行思考,其思维方向和模式的发散性有利于创造性能力的形成。
第二,开放题对教师角色的转变。在开放题引入课堂后,教师的角色定位发生变化,即在教学过程中,教师不是简单地、现成地给出答案,而是要引导、鼓励学生展开想象的翅膀,积极主动地思考问题。教师不仅仅是知识的传授者,更是教学内容和教学活动的设计者、促进者、示范者、组织者、调控者。
二、几种常见的开放题类型与策略
在初中数学教学中,为切实培养学生创新能力,近年来,出现一批符合初中学生的认知水平,设计合理的开放题。归纳起来,主要有以下五种类型。
1.条件开放型 所谓条件开放型试题是指在结论不变的前提下,条件不唯一的开放题。
例如:1、已知在ΔABC 和ΔDCB 中,AC=BD,若不增加任何字母与辅助线,要使 ΔABC ≅ ΔDCB,则还需添加一个条件是____。
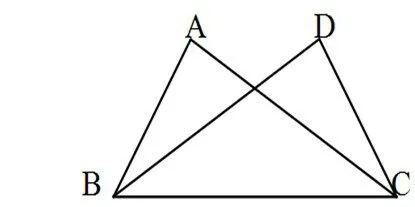
分析: 引导学生从三角形全等的判定可知,必须知道三个条件,而已知一个条件和写出一个条件,才两个条件是不满足全等条件,所以题中一定隐含一个条件,让学生说出隐含条件是BC=CB,所以已知两边,根据三角形全等判定需添一夹角∠ACB=∠DBC或一边AB=DC。
2.结论开放型 所谓结论开放型题是指其中判断部分是未知要素的开放题。这类题目,不同水平的学生可作出不同的回答,既能充分反映学生思维能力的差异,又能促使学生的思维发散。用于课堂教学将会有利于激发学生的好奇心,进而调动学习积极性,主动参与学习过程,且能培养学生的发散思维,使课堂充满活力和生机。
例如:(1)☉O 中,直径AB 垂直于弦CD,垂足为E,则可得到什么结论?
分析:让学生画出图形,根据圆的对称轴是直径所在的直线,引导学生通过沿直径AB 对折找到答案,从而得到垂径定理。
(2)写出经过两点(0,3)和(3,0)的二次函数解析式。
分析:引导学生从一般式y=ax2+bx+c和顶点式y=a(x -h)2+k入手,从而求出二次函数解析式;若从一般式入手,必须知道已知三点的坐标或三对函数对应值,由点(3,0)可知c=0,由另一点(0,3)求a,b;一般用赋值法,设a或b中一个为常数(若a=1)从而求解。也可以用顶点式求解,取某一已知点为顶点,如取(0,3)为顶点,设所求二次函数为y=ax2+3,再把(3,0)代入,可得a的值。
3.策略开放型 所谓策略型开放题是指条件与结论之间的推理是未知的,或解法有很多种的开放题.
例如:某广告公司要招聘广告策划人员一名,对张华、王明、李莉三名候选人进行了3 项素质测试,成绩如下表所示:如果你是公司总经理,你对这三位选手如何评价? 该录取哪一位?
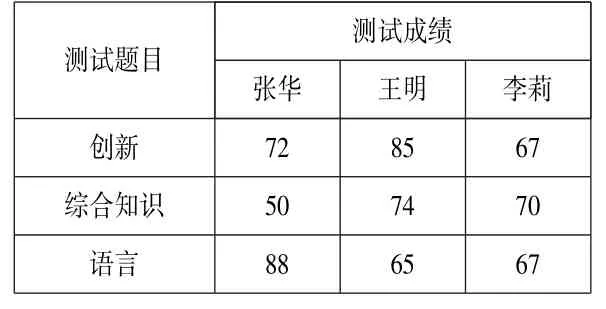
分析:我们总希望能选出最优秀人才来担任这一职位,能否只用绝对平均值的量化标准来选出最合适该公司的人才呢? 而广告职业本身最需要创新,其次是综合素质,最后才是语言,若用绝对平均值来招聘人才是不合适的。显然创新的权重最大,可将创新、综合素质、语言这三项成绩按3:2:1 的比例定各人的测试成绩来选拔人才较合适。
4.信息开放型 所谓信息开放型是指给出一定的信息,其条件、解决问题的策略与结论都要求学生从这些信息中寻找发现问题,从而探索解决问题的方法和途径,有利于提高学生分析问题和解决问题的能力。
例如:如果反比例函数的图象如图所示,那么二次函数y=kx2-k2x-1的图象大致为( )
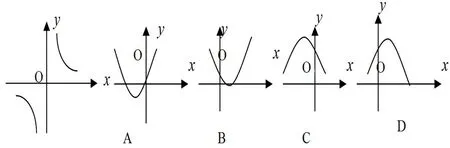
分析:对于二次函数的图象问题,要想确定它的图象规律,首先必须准确把握图象与a,b,c的关系,通常情况下,a确定它的开口方向,a,b共同确定对称轴的位置(或顶点的位置),c确定图象与y轴的交点的位置。首先由图象提供的信息可以看出反比例函数y=中,k >0,在二次函数y=kx2-k2x -1 中,k >0,开口向上,-k2<0,a,b异号,对称轴在y轴的右侧,-1<0,抛物线与y轴的交点在y轴的负半轴上。所以正确的是选项B。
5.综合开放型 所谓综合开放题是指只给出一定的情境,其条件、解题策略与结论都要求学生到情境中去自行设定或寻找的问题。综合开放型题目,较多关注学生创新意识、创造能力与数学应用意识。
例如:学校有一批复印任务,原来由甲复印社承接,按每100页40 元计算收费,现乙复印社表示:若学校先按月付给200 元的承包费,则可按每100 页15 元收费。那么选择哪一家复印社较合算?
分析:解决这类的问题是由复印页数的多少来决定收费的。假设每月复印x(x为非负整数)页,甲、乙每月实际收费分别为y1、y2,则y1=0.4x,y2=0.15x +200。
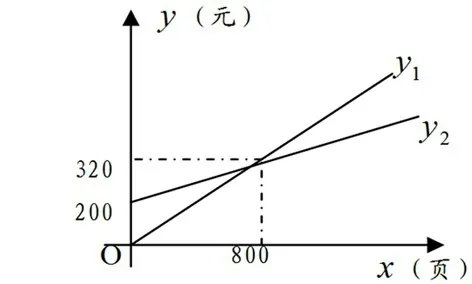
一种方法是:在同一坐标系中分别画出y1、y2的函数图象如图所示,由图象可知:
当0 ≤x <800 时,选择甲复印社合算;当x=800,选择哪一家都可以;当x >800 时,选择乙复印社合算。
另一种方法是:转化不等式关系来解决问题:(1)当y1<y2时,即0.4x <0.15x +200
解得:x <800 (2)当y1=y2时,即0.4x=0.15x +200 解得:x=800
(3)当y1>y2时,即0.4x >0.15x +200解得:x >800 所以当0 ≤x <800 时,选择甲复印社合算;当x=800,选择哪一家都可以;当x >800 时,选择乙复印社合算。
总之,在开放题的解答过程中,有时没有固定的、现成的模式可循,学生必须充分调动自己的知识储备,积极开展智力活动,打破原有的思维模式,用多种思维方法进行思考和探索。同时开放题有助于调动学生的学习积极性,激发学生的求知欲望与进取精神,有利于形成良好的思维品质和培养创新能力,提高学生分析问题、解决问题的能力。我们有必要认识开放题及其教学价值,加强对开放题的重视和研究,使开放题教学走进课堂。
