基于应力的非对称连续梁病害空间网格分析研究

李 玲， 艾贤臣

(1.新疆大学 建筑工程学院，新疆 乌鲁木齐 830047;2.新疆土木工程技术研究中心，新疆 乌鲁木齐 830047)

1 概述

预应力混凝土变截面连续梁桥应用至今，陆陆续续有一些桥梁出现了结构裂缝。交通运输部公路院曾对近200座大跨度预应力混凝土连续箱梁桥的开裂展开调研，经大量数据汇总显示，这些同类的连续箱梁桥的顶底板、腹板均有斜向开裂、竖向开裂、横向开裂等现象。其中微裂缝、中等裂纹、超限裂缝分别占33%、26%和41%。顶板居多，而腹板次之，均在86%以上，而腹板的开裂更是普遍问题。病害成因有很多，主要在于计算模型的不精细、预应力损失和重载交通等[1-3,7]。

目前，桥梁设计行业用于计算分析的程序有很多种，大多为平面杆系程序，计算效率比较高。其对于窄梁、单一箱室的桥梁基本满足工程设计的需求，有时面临复杂工程加上实体分析，也可应付。但是，针对旧桥加固时，以上所述的计算方法在分析桥梁病害的时候存在着不同的缺陷。平面杆系程序简单实用也是设计使用较多的计算模型，但不足以精细化。如：平面梁格法和单梁法只是根据刚度、截面特性等效的方式模拟箱梁的空间效应，但对宽箱梁、多箱室箱梁有诸多不足甚至不准确。实体模型的计算结果是对变形、应力、应变的综合，不能提取单项工况的计算结果，而一些桥梁往往是某一单项因素起控制作用，如：钢桥温度变化、索桥的恒载等，这时实体方法就显得与规范不相适应。由此可知，从精细化和应力完整性的角度来看，传统的计算方法来精准分析箱梁的受力特性存在着不足。因此，随着宽箱梁和多箱室的大量应用，箱梁的精细化模型就显得尤为重要。因为精细化计算模型可以得到任何箱梁的完整应力，对病害桥梁的成因分析更具有针对性[3-4,8-9]。

以下文中将简要介绍空间网格精细化分析的原理，以旧桥加固为工程案例，总结旧桥病害产生的原因，阐述其空间网格计算模型的特点，并分析超载下桥梁的空间网格模型和ANSYS模型的结果及评价治理超载后的空间网格模型精确性，为下一步桥梁维修加固提供参考。

2 空间网格模型简介

箱梁计算分析时，将箱梁的顶底板、腹板离散后形成各个板块，每块板均可以划分成十字交叉的网格，这些网格均采用正交梁格形式，所有的小型十字交叉网格利用刚度等效原则，替代十字交叉网格所代表的板元，也即N个十字交叉正交网格组成替代N块板元，由此替代整块顶底板、腹板，最终整个箱梁结构用空间网格来表示，这就是空间网格模型的原型。如图1所示，一个单箱单室的箱梁。顶底板、腹板用N个十字交叉的网格替代，每块板所用的正交网格都在各自的平面内，因此不同面内的正交网格离散后便成为一套空间网状模型[4-6,8-9]。

图1 箱梁网格化原理等代图Figure 1 Box girder grid replacement principle diagram

箱梁截面中的顶底板、腹板采用N个十字交叉网格来替代，其中N个十字交叉的正交网格代表了整个截面的弯剪扭的刚度。箱梁截面的材料可以是任意的，钢材或混凝土，或者其他材料。截面中材料可以任意组合，全钢、钢混、混凝土等均可。因此，空间网格的模型可模拟各种桥梁，如：宽箱梁、组合梁等，结构的具体形式可不受限制[8-9]。

3 工程概况

本工程是非对称的预应力混凝土连续梁，重载交通下运营多年，腹板出现诸多开裂等病害，跨径组合为(80+84+50)m，如图2所示，采用悬臂浇筑法施工。

图2 三跨连续梁立面图(单位：cm)Figure 2 Elevation view of three-span continuous beam (Unit: cm)

3.1 病害情况描述

检测结果显示，腹板裂缝居多，裂缝的形状从腹板底部向上发展逐渐变窄，一小部分裂缝与底板的横向裂缝连在一起。边跨右侧腹板近支点处，裂缝汇总起来约100 m，共计60条，其中超限裂缝(宽度在0.2 mm以上)达到40%，左侧腹板裂缝略少，超限裂缝比例达到37%，总长约55 m，共计44条，基本呈45°走向，位置在边跨中向支点方向。底板及腹板裂缝分布和走向分别如图3所示。

(a) 边跨内侧腹板裂缝示意图 (b) 边跨外侧腹板裂缝示意图

3.2 病害原因分析

检测结果可知，开裂的部位主要分布在左边跨的腹板，靠近边支点到跨中的裂缝分布呈竖向较多，在跨中附近有部分裂缝分布45°方向，超限裂缝(0.2 mm以上)比例约占36%。依照裂缝开裂方向和特征，加之本桥常有超载车和重车经过，可判断可能是由于频繁的重车或超限车辆过桥导致边跨箱梁腹板主应力或正应力超标。

4 空间网格模型分析开裂原因

4.1 网格计算模型简介

全桥的空间网格模型共划分为4 002个单元和3 500个节点，桥梁为正交，计算模型采用6DOF(6自由度)的空间梁格。在正常使用阶段计算时不考虑普通钢筋影响，只考虑预应力钢束的作用。根据检测结果和应力分布，下一步主要从应力的角度进行分析对比。

图4 空间网格模型Figure 4 Patial grid model

4.2 腹板开裂成因计算分析

为更全面、真实地反应重载等混合交通的影响，特查阅超载重车的历年记录与一定时间内的箱梁内外温度分布，从超重单车的影响面加载与考虑活载影响修正系数的角度出发，考查箱梁混凝土的应力分布情况。此计算阶段，参照规范中荷载组合的规定及计入活载影响修正系数，同时考虑超重车辆混入的影响。这样的计算处理方式既考虑了重载交通的荷载流对车道荷载的影响，又计入了最大重车混入的作用。

a.据实测超载车辆的空间网格模型分析。

此阶段的荷载组合：1×成桥阶段(考虑10年收缩徐变)+1×重车(影响面加载)+1×1.263车道荷载(引入活载影响修正系数)+1×腹板温差(横向温度梯度)+1×竖向梯度温度+1×人群荷载，从而对各种工况进行最不利效应包络，这样是为了既考虑了重载交通的荷载流对车道荷载的影响，又计入了最大重车混入的作用。将每项的计算结果进行包络取其最大值和最小值，之后将各个单项的最值进行叠加。左右腹板的正应力叠加计算结果分别如图5、图6所示，左右腹板的主拉应力叠加计算结果分别如图7、图8所示。

此阶段考虑了车道荷载的修正系数、重车混入影响、腹板横向温度梯度、桥面板竖向温度梯度、基础沉降及人群荷载的作用，将每项按照标准组合进行叠加。在荷载组合下，图5～图8分别列出了腹板正应力及主拉应力分布。腹板上下缘最大和最小正应力叠加的计算结果显示，左边跨下缘的拉应力(正应力)较大，合拢段区域腹板应力峰值接近6 MPa，应力超限的范围约40 m；中跨腹板下缘的拉应力最大达到2MPa，仅分布在跨中合拢段区域约2 m范围；左边跨左右腹板下缘主拉应力较大，其中外侧腹板下缘最大值达到2.7 MPa，离29#墩梁端约8 m的位置主拉应力达到1.5 MPa，基本与第30跨的腹板裂缝分布位置与范围相近。由此可知考虑了车道荷载的修正系数、重车混入影响、腹板横向温度梯度、桥面板竖向温度梯度、基础沉降及人群荷载的作用之后，左边跨腹板下缘出现了较大的拉应力(正应力)与主拉应力超标现象。其影响因素中，人群荷载、基础沉降、温度作用所产生的不利应力值较小，超载影响较大，也是裂缝产生较多的主要原因。

图5 右腹板上下缘正应力叠加结果图示Figure 5 Graphical illustration of the results of the normal stress overlay on the lower edge of the right web

图6 左腹板上下缘正应力叠加结果图示Figure 6 Graphical representation of the results of the superimposition of the normal stress on the lower web of the left web

图7 右腹板上中下缘主拉应力叠加结果图示Figure 7 Graphical illustration of the superimposed results of the main tensile stress at the middle and lower edges of the right web

b.实测超载车辆的ANSYS实体模型分析。

ANSYS实体有限元计算模型采取(SOLID45)模拟混凝土，选取(LINK8)模拟预应力钢束，梁身计算模型如图9所示，预应力筋计算模型如图10所示。经试算，①工况1： 1辆超载车通过左边跨情况：成桥阶段+1辆197 t超载重车(偏载)；②工况2：2辆超载车同时通过左边跨：成桥阶段+2辆197 t超载重车(中载)；③工况3：2辆超载车同时通过左边跨：成桥阶段+2辆197 t超载重车(偏载)，其中工况3引起边跨腹板应力超限，说明此种情况下较为符合实际车辆行驶轨迹，由此列出工况3的应力计算结果，如图11所示。工况3在2辆超载车偏载情况下，从左边跨外侧驶过时，梁底板外边缘纵向应力包络图可知，底板外侧拉应力区在8.5～47.5 m内，最大应力值为3.43 MPa，超过混凝土抗拉强度设计值，距离两端9 m处出现拉应力小峰值，拉应力大小为0.477 MPa。

图9 梁身计算模型Figure 9 Beam calculation model

图10 预应力筋计算模型Figure 10 Prestressed tendon calculation model

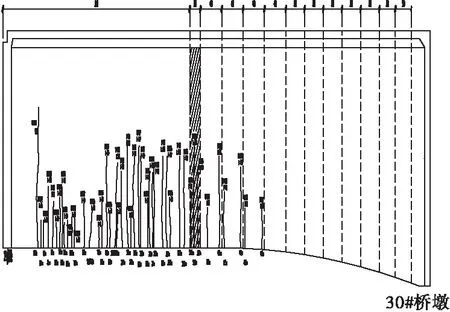
(a) 第30跨(东侧)外侧腹板裂缝分布图

ANSYS实体有限元模型计算结果表明：重车作用下，超载为腹板竖向开裂的主要原因，偏载对板底应力影响较大，偏载与中载最大应力比值为1.2。偏载效应明显，2辆超载车情况下板底最大纵向拉应力最大值和受拉区范围明显增加。

c.治超后的空间网格模型分析。

治理超载之后，为体现超载的影响，引入活载影响修正系数ξq到荷载组合。

① 依据当年4月～7月的交通量调研结果，交通量的实测值与设计值相比约等于2.152，则活载修正分项系数ξq1可取1.217。

② 大吨位超限汽车为简算车辆，考虑车辆混入率α，当α=0.147时，大吨位车辆混入率对应的活载分项系数ξq2为1。

③ 后轴超限的重车占据比例为β(5%≤β=14.8≤15%)，对应轴载下活载分项系数ξq3为1.16。

④ 综合以上①～③项 ，活载分项系数ξq=(ξq1ξq2ξq3)1/3=(1.217×1.0×1.16)1/3=1.112。

由此，按实际情况进行的荷载组合为：1×成桥阶段(考虑10 a收缩徐变)+1.12×车道荷载+1×腹板温差+1×梯度温度+1×人群荷载。

左右腹板的正应力叠加计算结果分别如图12、图13所示，左右腹板的主拉应力叠加计算结果分别如图14、图15所示。

图12 右腹板正应力计算结果Figure 12 Calculation result of right web normal stress

图13 左腹板上下缘正应力计算结果Figure 13 Calculation result of the normal stress on the lower edge of left web

图14 右腹板上中下缘主拉应力结果Figure 14 Result of Main Tensile Stress in the Middle and Lower Edges of the Right Web Plate

图15 左腹板上中下缘主拉应力结果Figure 15 Result of the main tensile stress at the middle and lower edges of left web

此阶段考虑了现状车道荷载的修正系数、腹板横向温度梯度、桥面板竖向温度梯度、基础沉降及人群荷载的作用，将每项按照标准组合进行叠加，图12～图15分别列出了腹板正应力分布及腹板主拉应力分布。由图12～图15可知，腹板上下缘最大和最小正应力的计算结果显示，左边跨下缘的拉应力(正应力)较大，合拢段附近腹板应力峰值达到3 MPa；左边跨左右腹板下缘主拉应力较大，其中箱梁外侧腹板下缘最大值达到1.5 MPa。根据2017年的实测现状交通流量，考虑修正活载影响系数并将温度、人群等荷载进行标准组合。计算结果表明，原出现裂缝的左边跨腹板，超限应力位置及范围有所减小，左边跨和中跨底板横向拉应力值也有所减小。可以说明治理超载之后，超载车辆的混入有所下降，减轻了对结构的负担。但是现状交通流量比原预测交通流量大，为保证结构安全、耐久，仍需严格控制超载车辆的驶入。

5 结论

通过空间网格模型、ANSYS实体模型及治理超载后的计算对比分析，得出以下结论：

a.考虑重载交通，建立空间网格模型和ANSYS实体模型，经计算分析得知，左边跨的腹板超限应力与实际裂缝产生的位置和范围相接近，可判断超载是腹板裂缝形成的敏感因素。

b.在重车偏载作用下，结构变形大已影响到桥梁安全性耐久性，因此，须严格控制超载车辆。

c.治理超载后，应力超限的量值及范围有所减小，为保证结构持续正常服役，可采用封闭裂缝和粘钢加固处理，并做定期检测。

d.空间网格模型能得出完整的箱梁应力分布，尤其是腹板等主拉应力。由此可知空间网格模型对箱梁桥开裂等病害的分析有较大的指导意义。