客车整备所三层作业平台可靠性分析*
2020-11-18杨朋朋宋国义张建华
杨朋朋,宋国义,张建华
(中铁第一勘察设计院集团有限公司,陕西 西安 710043)
0 引 言
随着我国高速铁路的快速发展,行驶速度也在不断迈上新的台阶,因此对列车的运营及维护的安全性和可靠性有了更高的要求[1]。完善的车辆检修修程是车辆安全运行的有力保障,三层作业平台作为车辆段内检修过程中必不可少的设备,它的安全性对于保证车辆检修人员的安全起到了至关重要的作用。三层作业平台主要完成动车组登车作业,在进行日常检修时,作业人员需要通过作业平台进行受电弓、空调设备、车门、车灯以及车内等检修作业。作业平台使用频率较高,因此对作业平台进行强度以及可靠性计算很有必要。目前国内已有的检修平台主要以混凝土结构以及钢架组合结构为主,与混凝土结构相比,钢结构具有材料强度高、重量轻,抗震性好、施工周期短、造型方便、对环境友好等优点[2-3]。在进行三层作业平台设备选型时,厂家为了保证安全性,采用了较大截面的工字梁,有限元结果计算显示该结果安全余量较大。对设备的安全性与经济性进行博弈,文中通过对钢结构三层作业平台进行可靠性分析,并对关键部件进行优化,减少用钢量,节约投资。
1 可靠性设计理论
结构在设计、制造以及使用过程中存在着许多对结构安全、适用以及寿命产生影响的不确定因素,如随机参数、模糊性以及决策者的技术水平等。传统的设计方法是根据安全系数来评估对结构安全的影响因素,并未考虑材料、载荷等的随机性对结构的影响。
随着计算机水平的快速发展,以概率理论作为评估机械结构可靠性的方法较为全面的考虑了工程结构中存在的随机因素,降低了对经验性的依赖,因此该方法已逐渐成为工程结构安全性评估与设计分析的一种常用方法,可靠度理论及方法的完善和发展对结构的安全评估及优化设计具有重要意义。
1.1 可靠性分析
可靠性分析是通过由状态函数的概率分布求出的可靠性概率,其结果是由影响状态函数的随机变量所决定的[4]。状态函数分别由式Z1、Z2表示:
Z1=[σ]-σ=g1(X),Z2=[s]-s=g2(X),
X=[x1,x2,…,xn]
(1)
式中:[σ]为结构强度;σ为计算应力;[s]为结构允许最大变形量;s为计算应力;X为随机变量参数;n为影响可靠度参数的数量。
一次二阶矩法是求解可靠度常用的解析方法,通过将非线性的状态函数展开成线性状态函数,从而计算出可靠性指标并求出可靠度。
各随机变量参数的均值为,将状态函数在均值点μ处展开成Taylor级数并保留一次项,得到:
(2)
则状态函数的均值和标准差为:
μZ=g(μX)
(3)
(4)
状态函数g(X)对各随机变量X求偏导为:
(5)
则可靠性指标和可靠度分别为:
(6)
(7)
1.2 可靠性灵敏度分析
可靠性灵敏度反应了各随机变量参数对机械可靠度影响的大小,灵敏度绝对值越大,说明该参数对可靠性影响越明显[5]。根据可靠度计算公式推导出各随机变量均值和方差的灵敏度计算公式为:
(8)
(9)
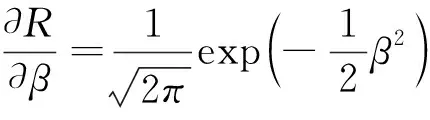
(10)
(11)
(12)
2 三层作业平台强度分析
钢结构作业平台属于乙类建筑,因此,钢架按7度抗震设防。环境温度:-5~45 ℃,相对湿度≤95%RH。首先根据某客车所三层作业平台,建立三层作业平台三维模型。整个钢结构平台长 510 m,其中一层为地面,二层作业平台距地面高1.25 m,三层作业平台距地面高4.0 m,作业平台宽 0.8 m,二层和三层设有高度为1.2 m不锈钢防护栏。整个钢结构平台由双排 H 型钢支撑立柱承受所有重量,两排立柱中心间距9.0 m。立柱之间通过纵梁连接,纵梁长度为9 m,纵梁中间采用方管横梁连接,方管长度为800 mm。作业平台现场实物如图1所示,建立作业平台三维模型如图2所示。
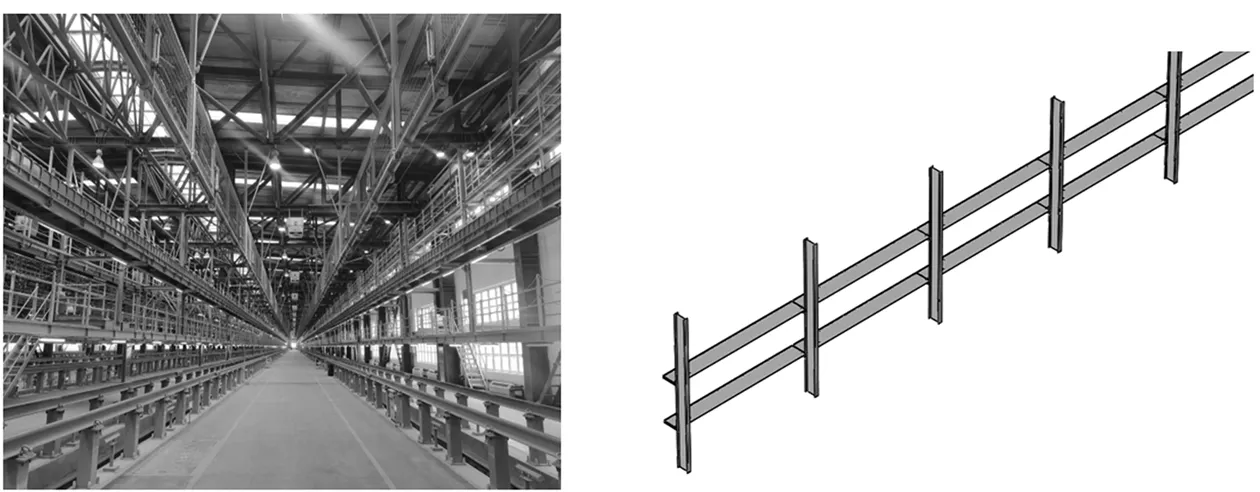
图1 三层作业平台现场图
2.1 关键部位选择
三层作业平台主要承受自重、安装设备以及作业人员的载荷,载荷形式相对稳定,根据作业平台在检修过程中的实际受力情况,选取6处关键部位进行强度分析,选择如图3所示。
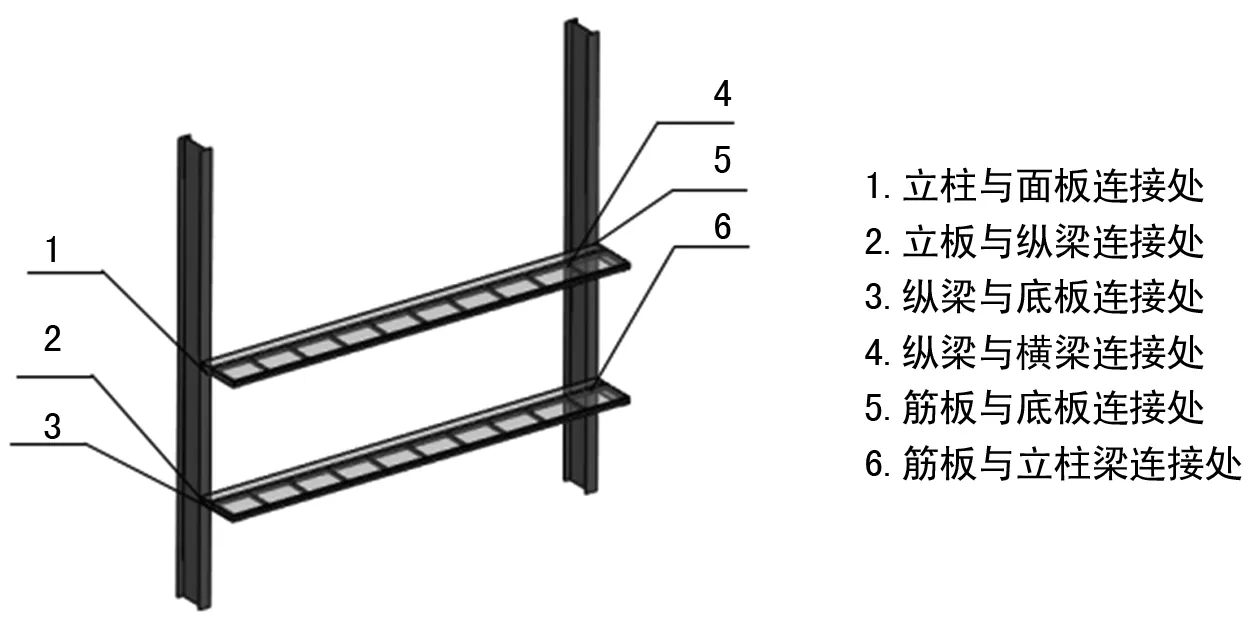
图3 关键部位选择
2.2 材料属性
根据钢结构设计规范,H型钢及方管主要材质为Q235,材料常数如表1所列。
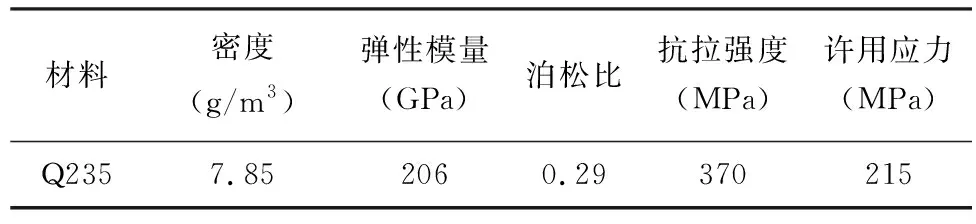
表1 材料属性
2.3 有限元模型建立
原结构纵梁采用窄翼缘H型钢,截面尺寸为H200×100 mm×5.5 mm×8 mm,方管尺寸为120 mm×120 mm×8 mm。通过有限元计算可得,该截面安全余量较大,根据GB/T11263-1998,选取同类型H型钢,纵梁尺寸为H175×90×5×8,纵梁中间采用方管横梁连接,方管尺寸为60×60×6。在二层和三层纵梁上铺设10 mm厚花纹钢板。
由于作业平台零部件较多,且每一跨之间的结构完全相同,为了节约计算资源、提高计算效率,选取任意一跨进行疲劳可靠性分析,且对不承重、不影响求解结果的孔以及圆角进行模型简化。选取Solid 185实体单元对钢结构作业平台进行结构离散,由于横梁与纵梁之间采用焊接连接,为了防止在焊接过程中焊接部位出现应力集中,因此对焊接部位采用更加精细的网格划分,建立三层作业平台有限元模型如图4所示,局部网格精细化划分如图5所示,最终得到单元数为35 342个,节点数为231 404个。

图4 有限元模型
2.4 静强度分析
根据材料属性,考虑作业平台自重,根据文献[1],平台承受载荷为 200 kg/m2;立柱梁的上端与屋顶结构相连接,下端固定于地面上,对作业平台进行有限元分析,关键部位的应力结果见表2所列。
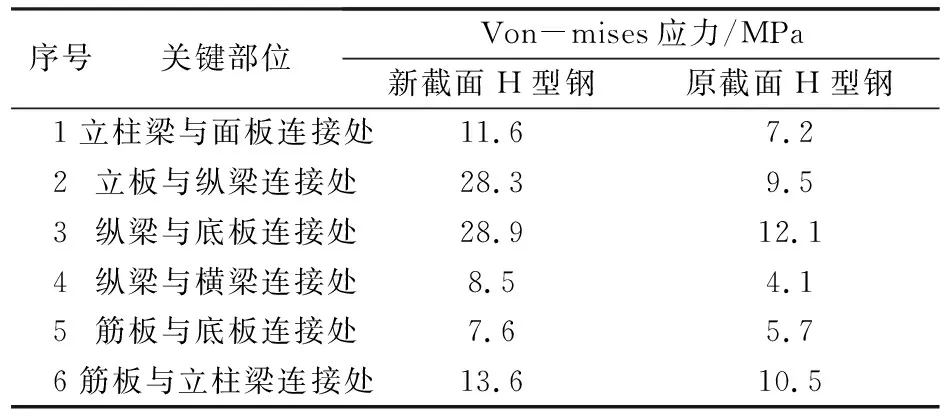
表2 有限元分析结果
根据计算结果可得,最大Von-mises应力为58.9 MPa,小于结构许用应力215 MPa,变形为8.8 mm,小于30 mm[6],因此静强度满足设计要求。
3 可靠性灵敏度分析
根据三层作业平台的静强度分析,可靠性状态函数为:
(13)
(14)
由式(15)可以看出影响作业平台可靠性的参数为:作业平台结构许用应力[σ];载荷q;变形[s],弹性模量E,其假设都服从正态分布[5,7-8],则参数如表3所列。

表3 参数表
计算得到两种截面下作业平台可靠度如表4所列,其中状态函数g1(X)可靠度为R1,状态函数g2(X)可靠度为R2,计算结果如表4所列。
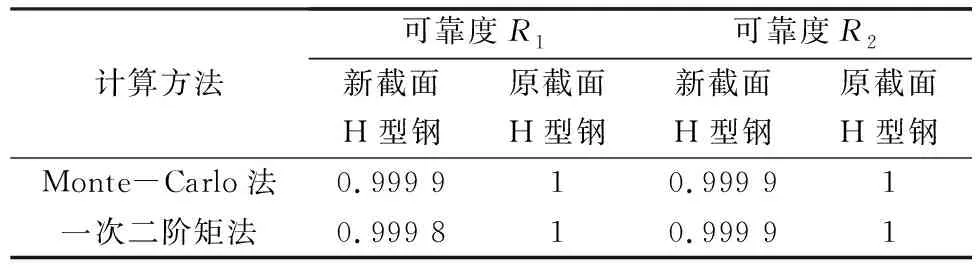
表4 两种计算方法下的可靠度值
如表所示,新截面H型钢在两种不同方法下的可靠度值均大于0.997 4,因此满足了3σ设计要求,且两种方法计算得到的可靠度结果非常接近,因此计算结果是可接受的。对两种截面下的三层作业平台用钢量进行计算,计算结果如表5所列。
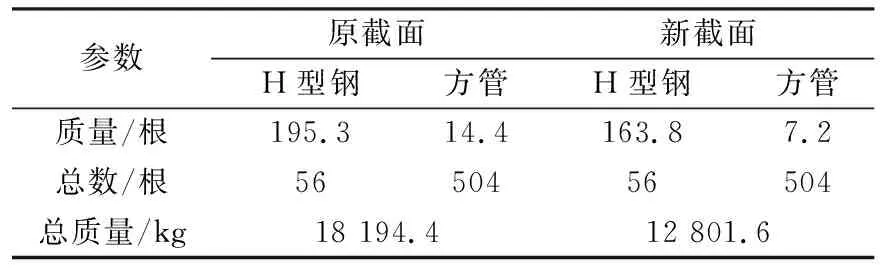
表5 两种截面下的用钢量
4 结 论
(1) 选取新截面的H型钢及方钢,对新截面作业平台进行有限元分析,结果显示,作业平台最大应力发生在纵梁与底板连接处,值为28.9 MPa,小于材料的许用应力215 MPa,静强度满足设计要求。
(2) 采用一次二阶矩法及Monte-Carlo法对新截面进行可靠性分析,可靠度计算结果均大于0.997 4,因此满足了3σ设计要求。
(3) 根据三层作业平台实际尺寸,对两种不同截面下的H型钢用钢量进行计算,结果如下表计算结果显示,三层作业平台采用新截面相对于原截面,型钢用量可节约29.6%。
在保证设计安全裕量的基础上,对H梁截面尺寸进行了重新选型,通过分析可得,新的截面尺寸不仅减少了三层作业平台自重,也降低了三层作业平台设备的投资,分析结果对于结构的改进再设计具有一定的参考价值。
