基于改进SOA算法自整定PID系统优化研究

葛育晓，赵荣珍

(兰州理工大学机电工程学院，甘肃兰州 730050)

0 引言

PID 控制是一种相对成熟的控制策略，因其算法简单、容易实现、鲁棒性好、可靠性高、适用场合广泛等特点，目前已变成了工业控制系统首要考虑的控制方法[1]。但是由于目前工业控制现场具有非线性、大时滞、高阶等特点[2]，而传统的PID优化控制方法很难取得最优参数，且很容易产生超调以及震荡现象等[3]，因此对于PID控制器参数的优化调整，对于实际工程有着重要的研究价值。在PID参数优化整定中，传统的参数整定方法如Ziegler-Nichol (Z-N)法[4]难以取得最优或接近最优的PID参数，获得很好的控制性能，因此很多学者提出了各种智能优化整定方法：傅晓云等[5]将遗传算法引入了PID控制器的参数优化，但遗传算法本身的整体结构比较复杂，参数设置较多，计算量大；宋荣荣等[6]人将粒子群算法运用于PID控制器的参数寻优，但基本粒子群算法存在早熟的缺点，算法容易收敛到局部最优，导致整定的误差偏大；刘冰艳等[7]人将神经网络用于PID参数优化，但神经网络结构确定困难，且隐含层数目、神经元个数以及初始权值等这些参数的选择没有一套标准系统的方法，通常依赖人的经验。

人群搜索算法(seeker optimization algorithm，S-OA)[8]是最近比较新兴的群智能优化算法，是通过对人的搜索行为进行分析，进而模拟后提出的算法，该算法鲁棒性好，而且算法整体实现简单，具有搜索性能强等特点。目前，很多学者对人群算法的改进做了相关研究。文献[9]引入对立的学习方法并与之结合，应用于混沌系数的参数估计，效果良好；文献[10]针对算法后期易陷入局部最优，引入了模拟退火思想，提高了算法的全局搜索能力；文献[11]针对搜索步长和方向的惯性系数的选取方法进行了修改，取得了一定的效果。

基于以上的分析，针对PID参数优化整定的难点，本论文提出一种混沌自适应人群搜索算法(chaos adaptive seeker optimization algorithm，CASOA)，将此算法运用于PID控制器参数的自适应优化整定。并且通过Sphere等3个经典测试函数与其他算法相比较判断本文算法的性能好坏，最后利用MATLAB平台，设计了基于CASOA算法的PID控制参数整定优化的算法程序，并选用文献[8]中采用的二阶惯性加纯迟滞系统的数学模型进行模拟仿真，验证本文提出的优化方法较文献[8]的优越性。

1 基本原理简介

1.1 PID控制器基本原理

PID控制器基本控制原理如图1所示。

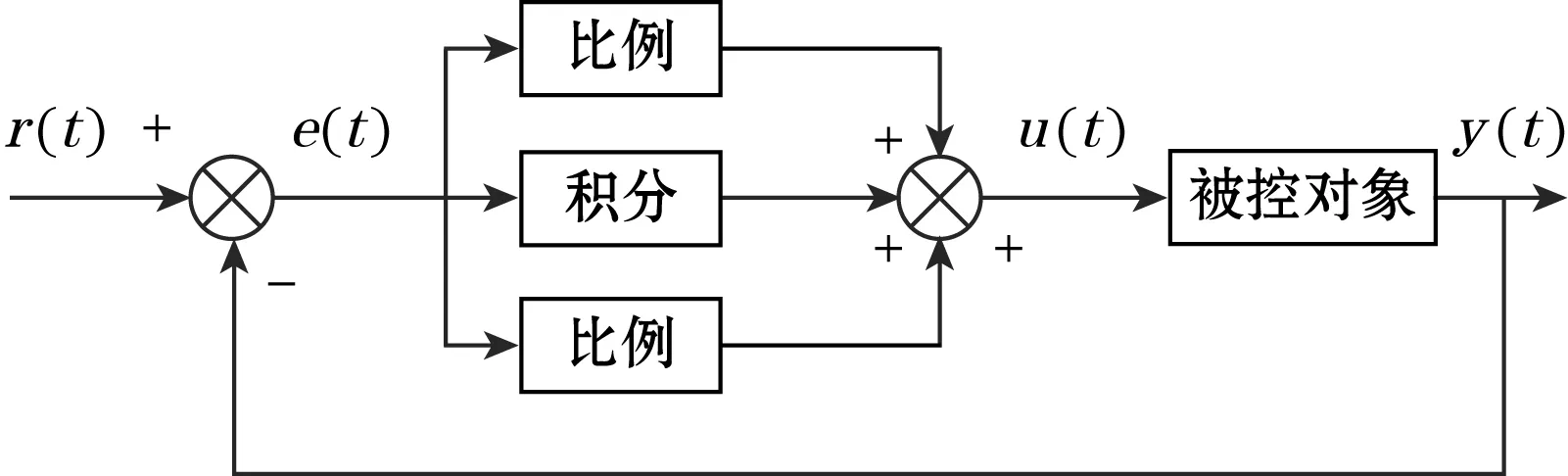
图1 PID控制系统框架

PID控制是将给定值r(t)和实际输出值y(t)得到的控制偏差

e(t)=r(t)-y(t)

(1)

再经P、I、D3种计算方式组合计算出控制器的输出值，对被控目标进行反馈调节。PID控制规律为：

(2)

将式(2)写成传递函数的形式为：

(3)

式(3)中不同的比例系数Kp、积分时间常数Ti和微分时间常数Td的大小对于系统的响应速度、回调速度以及调节时长等都有不同的影响。PID控制器参数优化的目的就是在保证整个系统稳定的前提下，优化调整3个控制参数使得系统的综合性能得到提高。

1.2 基本人群搜索算法

SOA算法是一种模拟人的搜索行为的智能算法，是借助人工智能、群智能和脑科学等对人的随机搜索行为进行分析后得出的研究成果[12-13]。

1.2.1 搜索步长的确定

人群搜索算法具有一个特点——“若目标函数小那么搜寻步长就小”，因此选用了高斯隶属函数来度量步长变量，如式(4)所示

(4)

式中：uA为高斯隶属度；x为输入变量；u、δ均为隶属函数的参数，并设定最小隶属度umin=0.011 1。

搜索步长由式(5)所确定

(5)

式中：aij为j维连续搜索空间的搜索步长；uij为j维搜索空间内目标函数值i的隶属度，具体公式为

uij=rand(ui,1),j=1,2,…,D

式中：ui为目标函数值i的隶属度；D为搜索空间维数。

式(5)中δij是高斯隶属函数的参数，其值由下式确定，即：

1.2.2 搜索方向的确定

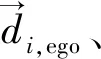
(6)

(7)

(8)

式中：gi,best为个体所在邻域的群体历史最优位置；pi,best为个体搜寻经过的最优位置；xi(t)为个体当前位置。

搜寻者通过式(9)对3个方向综合考虑确定最终搜索方向：

(9)

式中：ω为惯性权值；φ1和φ2表示[0,1]内随机数。

1.2.3 搜寻者个体位置的更新

确定搜索步长和方向后，位置更新依据式(10)和式(11)：

Δxij(t+1)=aij(t)dij(t)

(10)

xij(t+1)=xij(t)+Δxij(t+1)

(11)

2 人群搜索算法改进策略

标准人群搜索算法与其他群智能搜索算法有着相似的缺陷，即随着算法迭代的不断进行，搜寻个体位置的不断更新变化，后期可能会出现大量搜寻个体出现局部聚集的情况，搜索过程停滞，而且导致整个种群个体多样性减少，最终算法收敛的结果容易陷入局部最优。因此为提高算法的搜索精度和收敛速度，以及解决算法后期种群个体的多样性缺失的问题以及算法后期增加种群个体的多样性，本文引入了以下几种改进策略，从而使得算法合理有效的避免上述缺陷。

2.1 惯性权重随机动态变异

标准SOA算法，惯性权重的迭代修正采用梯度下降法。但是梯度下降法中的学习速率是一个定值，目前取值并没有一套科学合理的理论指导，大多都是经验取值，“学习速率过小，导致算法收敛速率很慢，反之，过快”，因此学习速率的最优解的确定仍是一个难点，并且梯度下降法在迭代过程中，个体位置越趋近于目标，那么步长就会越小，收敛速度就会越慢，因此倘若搜寻个体的位置靠近局部最优位置时，搜寻个体的位置更新速率会减慢，进而影响整个算法收敛到全局最优解的速度。因此，本文提出随机惯性权重变异策略，如若个体在初始状态时的位置就接近最优位置，随机产生的惯性权重值可能相对较小，可以加快整个算法的收敛速度[14]，并且采用随机惯性权重变异策略能够克服梯度下降法中权重值的线性递减造成算法不能收敛到最好点的局限性。本文将惯性权重 的计算方式修改为式(12)

ω=μmin+(μmax-μmin)·rand(0,1)+σ·N(0,1)

(12)

式中：方差σ=0.2；μmin和μmin分别为随机动态惯性权重最大、最小值。

2.2 边界反射策略

在运动过程中任意一个个体的位置超出给定空间的限定就会对算法的结构给予一定的破坏。标准SOA算法中对边界值处理的方法是把超出边界范围的搜寻者固定到边界上，即将它设定为边界值，从而能够继续保持算法结构不被破坏，但这样做可能会造成大量的搜索者聚集在边界上的情况。因此，为了避免此种情况发生，受反向学习的启发，提出了简化的反向学习策略——边界反射策略，将超出边界的搜索者经式(13)反射投影到种群边界内，既克服了传统处理方法的缺陷，又增加了种群的多样性，使得算法的收敛精度有了一定的提升。其基本处理思想如下：

(13)

式中：swarm(i,:)为第i个粒子的更新位置；popmax为上界；popmin为下界；rand为0～1之间的随机数。

2.3 混沌优化

混沌优化方法是一种全局优化算法，混沌变量虽杂乱无章但却具有一定的规律性，其遍历性特点能够遍历某一局部范围内的所有状态且不重复，避免算法陷入局部极值点。Logistic方程就是一个典型的混沌系统，如式(14)所示

yn+1=μyn(1-yn)(n=0,1,2,…,0≤μ≤4)

(14)

式中：yn为系统输出；μ是控制参数；n是迭代次数。

如图2所示为Logistic混沌映射的混沌图形。从图中可以看出：μ在区间[0，1]上无论取何值，系统最终都会收敛于0；当1<μ<3时，系统的极限行为会趋于一个非零点，μ不同，非零点不同；而当3<μ<3.6时，系统方程的迭代开始出现周期行为，随着μ的不断增大，周期的长度也会相应的增加；最终当3.6<μ<4时，系统进入混沌状态，整个系统方程迭代运行的轨迹随着μ的持续增大在周期状态和混沌状态之间来回切换，直到μ=4时系统处于完全混沌状态，在[0,1]区间上均匀分布。

图2 Logistic混沌映射分岔

为解决标准SOA算法在后期易陷入局部最优，导致算法停滞的问题，本文利用混沌变量的便利性这一特点，通过对最优位置的二次扰动，增加了种群个体的多样性，并使得搜寻个体的位置更新更加多元化，更符合现实中因素的多变性这一普遍规律。

具体算法中混沌优化部分伪代码如下所示。

while stopping criterion is not meet do

Mapxgbestto the domain [0,1] of the Logistic equation by Eq.(15)；

(15)

Iteratively obtain a set of chaotic sequences by Eq.(14);

Reverse mapping the chaotic sequence and mapping back to the original space by Eq.(16);

(16)

Evaluate the fitness of each particle in the current sequence，and select the corresponding value when the fitness is optimal.

A searcher is randomly selected from the current searcher population to replace the extracted searcher.

The algorithm contimues to the next step.

3 基于CASOA的PID控制器优化设计

3.1 CASOA-PID控制器原理图

利用CASOA算法通过对系统采集信号得出的偏差情况的优化处理，调节控制器的Kp、Ki、Kd3个参数，使得控制器的综合性能达到最优，使其满足工作要求。其原理如图3所示。

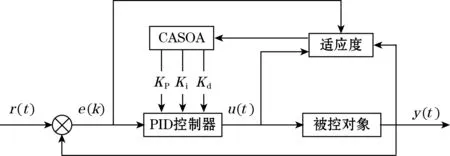
图3 CASOA-PID控制器原理图

3.2 适应度函数的确定

本文为获得满意的迭代过程动态特性，采用性能指标加权的方式来构造算法的目标函数。对于系统阶跃响应，采用误差绝对值时间积分性能作为目标函数的主要部分，如式(17)所示。

(17)

式中：e(t)为rin(t)和yout(t)之间的误差值；u(t)为控制器输出，采用u(t)的平方项为了防止控制能量过大；ω1和ω2为权重常数，范围在[0,1]之间。

并且针对超调现象这一问题，性能指标中引入了惩罚措施，将超调量一并作为最优性能指标中的一项，原理如式(18)所示。

Ife(t)<0

(18)

式中：ω3为权值，且ω3>>ω1；Δe(t)=y(t)-y(t-1),y(t)为被拉对象输出；通常ω1=0.999，ω2=0.001，ω3=100。

3.3 具体CASOA-PID算法的实现步骤

采用CASOA算法优化PID控制器3个参数的具体步骤如下：

Step1：初始化种群。给定种群维数、规模等一系列参数值，随机生成种群位置矩阵。

Step2：评判各组Kp、Ki、Kd中每个搜寻者个体的位置优劣。根据式(18)计算每个搜寻者个体的适应度值。

Step3：记录并更新搜寻者的个体最优以及全局最优。

Step4：搜寻者位置更新。根据式(5)和式(9)计算每个搜寻者个体的搜索步长aij(t)和搜索方向dij(t)；然后依据式(10)和式(11)对每个个体进行位置的更新。

Step5：混沌优化。利用混沌Logistic方程对搜寻者最优位置进行混沌优化。

Step6：判定条件满足与否。若不满足，则返回Step2，否则，搜寻停止，输出控制器Kp、Ki、Kd3个参数的优化结果。

Step7：算法结束。

4 算法的性能分析

4.1 测试函数的设定

本文通过选取3个典型测试函数测试其性能，并对比标准PSO、CPSO、标准SOA算法的优化效果来证明本文提出的算法的优越性。3个标准测试函数参数设置见表1。

表1 标准测试函数参数设置

测试函数1为Sphere函数

(19)

测试函数2为Schaffer函数

(20)

测试函数3为Rastrigin函数

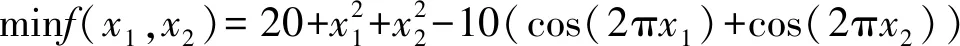
(21)

4.2 参数设置

本文选取了4个算法进行性能比较，即标准PSO、CPSO、标准SOA和本文提出的CASOA算法，本着算法比较参数设置一致的原则，各算法的基本参数设置如下：

标准PSO算法：种群规模100，惯性权重1，个体学习系数1.494 45，全局学习系数1.494 45，最终迭代次数100，重复实验次数10。

CPSO算法：种群规模100，最终迭代次数100，混沌系数2，重复试验次数10。

标准SOA算法：种群规模100，最终迭代次数100，最大隶属度值0.950 0，最小隶属度值0.011 1，权重最大值0.9，权重最小值0.1，重复实验次数10。

CASOA算法：种群规模100，最终迭代次数100，最大隶属度值0.9500，最小隶属度值0.0111，权重最大值0.9，权重最小值0.1，混沌系数3.5，重复实验次数10。

以上算法的仿真硬件设备为Intel core i5-4200U 1.60 GHz 2.30 GHz 8GB RAM 64位操作系统笔记本；仿真软件环境Win10 MATLAB R2015b。

本文通过计算平均值来评价算法收敛精度，运用标准差来评价算法稳定性。实验数据如表2所示，为使所得结论更具有普遍性，因此数据矩阵是随机产生的，所得结论不一定每次都是最优的。上述数据结论为性能结果相似的10次数据的平均值和标准差，除去了异常状态。

表2 不同算法的收敛精度和稳定性比较

从表2得出：改进的人群搜索算法CASOA在3个测试函数上无论是适应值平均值还是标准差均具有明显优势。具体来讲，CASOA在单峰函数Sphere上相较其他算法在收敛精度及稳定性上有较大的提高，C-ASOA相比于SOA平均值从39.479 1提升到了3.815 9，较CPSO也有一定幅度的提升，采用了随机动态惯性权重策略保证了搜寻者个体运动的自由灵活。此外，C-ASOA在多峰函数Schaffer和Rastrigin上算法的收敛精度和稳定性也有很好的表现，均比其他算法有所提升，本文引入了边界反射策略，将群体中因位置更新而脱离搜寻范围的个体经边界反射策略重新定义到有效范围内，既增加了种群个体的多样性，又避免了标准SOA算法中因大量搜寻者聚集在搜寻范围边界使得算法收敛到局部极值点的结果，而且本文算法还引入了Logistic混沌优化，将每次搜寻到的最优解再经Logistic混沌映射进行二次扰动，大幅的增强了搜寻个体避免陷入局部最优位置的能力，使得算法在全局寻优方面也有较强的优势。

5 仿真实验结果分析

5.1 控制对象及仿真条件设置情况

大部分的实际控制工程都是复杂的高阶系统，许多系统常常被近似为一阶惯性和二阶振荡的典型的叠加系统。本文为测试改进算法的性能优势，以及体现本文方法的优势，最终选取了文献[8]中的二阶惯性加纯迟滞系统作为被控目标进行Matlab模拟仿真实验。系统传递函数为

设搜寻者群体规模为30，迭代次数200，Kp、Ki、Kd3个优化参数搜索领域均为[0，100]，Wmax和Wmin分别为0.9和0.1，混沌系数μ=2，以0.1 s为采样间隔，单位阶跃信号作为本次模拟仿真的输入信号，整体仿真时间设为10 s，能够完整的体现整个系统的调节过程。

5.2 实验结果及分析

利用MATLAB等仿真工具对标准SOA和CASOA算法进行仿真，模拟优化过程，得两种算法的适应度函数优化曲线以及控制系统阶跃响应输出曲线和误差曲线，分别如图5、图6所示。

图5 CASOA和SOA适应值变化曲线

(a)阶跃响应曲线对比

(b)误差曲线对比图6 CASOA和SOA阶跃响应变化与误差对比

由图5可以看出两种算法的适应度值收敛的情况，改进的CASOA算法在迭代20次左右便开始快速收敛，收敛精度高，且稳定性很好；而标准SOA算法从图中可以很明显的看出，算法在收敛到20代和30代左右均出现了陷入局部最优的趋势，最终在50代开始收敛，收敛速度相对缓慢，因此相比之下CASOA算法收敛速度与精度明显优于文献[8]中标准SOA算法，具有更好的局部搜索与全局搜索能力。

图6中，阶跃响应输出与误差比较曲线显示：改进的人群搜索算法CASOA优化的PID控制器综合性能与标准SOA算法相比有一定的提升，达到了良好的控制效果。具体来说：CASOA-PID控制系统上升时间快，仅1.5s左右，有轻微超调现象，但快速性和稳定性能更好，而文献[8]中的SOA-PID控制系统虽无超调，但上升时间缓慢，响应速度慢，且调节时间过长，4 s左右才达到稳定状态。因此，对于控制工程中大多数高阶、非线性带有迟滞环节的系统，采用CASOA算法对PID控制器进行参数优化，相较于文献[8]中的标准SOA算法得到的控制器具有更好的性能效果。

6 结论

PID控制器参数的选取对于整个系统的平稳、精度、响应速度等有着举足轻重的意义，为提高PID控制器的控制效果，本文提出了一种混沌自适应人群搜索算法，该算法引入随机惯性权重策略，有效的克服了标准SOA算法中权重采用线性递减造成的算法不能收敛到最好点的局限性；采用边界反射策略，既避免了传统处理方法使大量搜寻者聚集在边界上的缺陷，又增加了种群中的个体的多样性，减小算法迭代后期因个体的多样性降低使得算法收敛到局部最优的可能性；同时算法进一步结合了混沌优化算法，对当前搜索到的全局最优位置进行混沌优化，通过对个体位置的二次扰动从而解决了因个体位置更新停滞导致的算法早熟而收敛到局部最优的问题。通过3种典型测试函数与其他算法对比验证其在精度与速度上的优越性，并且将其应用于PID控制器的参数优化，本文通过对二阶惯性加纯迟滞系统进行模拟仿真，最终结论显示相比于标准SOA算法优化的PID控制器，改进的控制系统具有更快的响应速度，更高的稳定精度，良好的鲁棒性，能够保证良好的控制性能，因此为后续PID参数优化方法提供了一定的参考依据。

本工作得到了兰州理工大学红柳一流学科建设项目支持。