一种基于时间序列的光伏出力预测方法研究
2020-11-18薛靖飞
张 娜 薛靖飞 张 晶
(1.内蒙古工业大学 内蒙古 呼和浩特 010008;2. 内蒙古华能呼伦贝尔公司东海拉尔发电厂 内蒙古 海拉尔 021008)
引言
随着光伏发电技术的迅速发展,光伏发电在电力系统中的比重逐年增加。2018年全世界新增光伏装机总量超过100GW,2019年新增121GW,到2019年底,光伏装机总容量已达到了626GW。但光伏的间歇性、随机性问题更为凸显,为了更好地接入光伏,对其进行准确地预测是目前最为基础的工作之一。
光伏发电前景良好,世界各国都进行了对其预测的研究。早在2005年世博会上,日本就展示了NTT Facilities公司的光伏发电预测技术预测330KW光伏发电项目[1]。我国对光伏发电输出功率的预测起步较晚,但也取得了良好的进展。如宁夏供电公司的光伏发电项目,中国电力科学研究院和湖北省气象部门合作并开发的光伏发电输出功率预测系统等。对国内外的研究方法进行总结,可以发现目前对于光伏输出功率预测的方法基本可以分为时间序列法[2]、人工智能法[3]、物理模型参数法等。时间序列法运算速度快,但若天气情况改变,预测精度就不高;人工智能法建模方便,但部分方法容易陷入局部最优,影响预测精度;物理模型参数法建模过程复杂,参数评估困难。本文选取时间序列法进行预测,为了避免数据变化对模型的影响,采用相似日的方法对模型输入样本进行改进,利用选取样本前后预测结果进行比较,验证本文所提方法的有效性。
1 基于ARIMA的光伏出力预测模型
1.1 自回归移动平均模型(ARIMA)
自回归移动平均模型的简称是ARIMA模型,全称是Autoregressive Integrated Moving Average Model。是美国学者金肯和波克斯于1970年提出的[4]。ARIMA模型的基本思想:首先将预测对象按照时间经过的顺序排列数据,并作为一个随机序列来处理;其次基于时间序列的自相关分析,选择出适当的参数,用数学模型近似描述这个序列;最后确定了模型后,就可以利用模型和过去的数据去预测未来的数据。ARIMA模型不仅考虑了数据的变化对时间序列的依赖,还考虑在数据变化过程中各种随机扰动的干涉。这是近年来使用最广泛的方法之一。
ARIMA是ARMA(自回归滑动平均模型)的扩展模型。ARMA可以用于平稳时间序列建模预测,由自回归模型和滑动平均模型为基础混合而成。
自回归模型AR(p)可以用如下公式表示:
Xt=φtxt-1+φ2xt-2+……+φnxt-n+εt
(1)
滑动平均模型MA(q)可以用如下公式表示:
Xt=εt-θ1εt-1-θ2εt-2-…-θnεt-n
(2)
ARMA(p,q)模型可以用如下公式表示:
Xt=φ1xt-1+φ2xt-2+…+φnxt-n+εt
-θ1εt-1-…-θnεt-n
(3)
其中φi为自回归参数;θj为滑动平均参数;
εt为高斯白噪声。
当q为零时ARMA模型就退化为AR模型,当p为零时ARMA模型就退化为MA模型。
ARIMA(p,d,q)模型是ARMA模型的一种扩展,“d”表示差分的阶数。可以用于非平稳时间序列数据建模预测,可以表示为:
(4)
当d=0时ARIMA模型就退化为ARMA模型。
1.2 相似日选取
光伏发电出力和太阳辐射量密切相关,气候又直接影响太阳辐射量,因此以太阳辐射量为依据通过欧式距离公式把样本数据分为2种基本的天气类别,晴天与阴天,然后分别建模预测。
1.3 预测误差
本文利用平均绝对百分比误差MAPE来作为模型的评价指标,MAPE的计算公式为:
(5)
式子中:N为样本数;Sn为真实值;Yn为预测值。
1.4 模型预测流程
ARIMA模型预测主要分为建模和预测两个步骤。选取相似日样本构建ARIMA模型,模型的建立流程,如图1所示:

图1 ARIMA模型的建立
2 算例建模及结果分析
2.1 晴天预测过程及结果分析
2.1.1样本数据平稳化
本数据为内蒙某光伏电站2019/01/01-2019/06/30的光伏出力数据,时间间隔为15min。选取其中部分样本作为测试数据。首先对样本数据进行ACF与PACF检验,自相关函数(ACF)是把一个序列之中的数据互相对比,结果代表了同一序列之中不同值的相关性。偏自相关函数(PACF)是除去中间变量的干扰后,两个变量之间的相关程度[5]。由于篇幅原因,仅显示晴天情况下测试数据的情况,如图2、图3所示:

图2 ACF检验

图3 PACF检验
根据图2和图3分析,可以看出数据不稳定,不符合ARIMA模型的要求,需要对数据进行差分处理。对不稳定的数据进行n阶差分能得到稳定的数据,但差分过多会导致数据的流失,所以这里先进行一次差分,查分后与差分前数据对比,如图4所示:

图4 一次差分数据与原数据对比
对一次差分数据进行ACF与PACF检验,如图5、图6所示:

图5 一次差分数据ACF检验
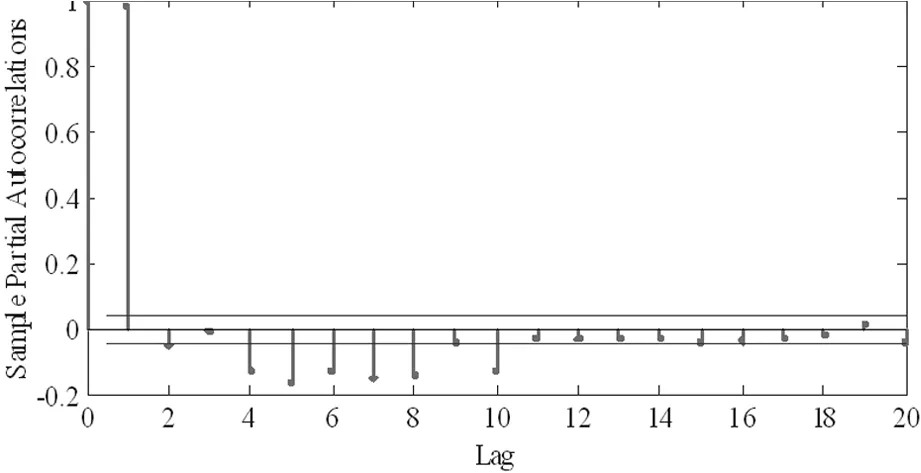
图6 一次差分数据PACF检验
一次差分数据ACF与PACF在延迟几阶之后趋于稳定,符合平稳性要求。并对差分数据进行ADF检验和KPSS检验,得到ADF =1,KPSS =0,通过检验。
2.1.2 模型的定阶和建立
根据图5和图6分析,一次差分数据的ACF与PACF在延迟10阶后趋于稳定,符合ARIMA模型的要求。
ARIMA(p,d,q)模型中的d为1,先假设p,q最大为10,然后在p(1-10),q(1-10)范围内,根据AIC选取适当的阶数。AIC(信息准则,即Akaike information criterion),是判断模型拟合优良的一种常用标准。在一般的情况下,AIC的计算公式为:
AIC=2*K-2ln9(L)
(6)
式中:K是参数的数量,L是似然函数。
表1为挑选出的几种AIC最小的模型。

表1 晴天ARIMA模型pq值的选择
根据AIC准则选取出最适当的阶数p为10,
q为8。建立ARIMA(10,1,8)模型,并用前21天晴天光伏功率数据训练模型,所得模型为:
yt-0.2583yt-1+0.1520yt-2+0.8517yt-4+0.6257yt-3+0.4986yt-5+0.2457yt-6-0.8433yt-7-0.2490yt-8
-0.0831yt-9-0.0609yt-10=εt-0.0131εt-1-0.1399εt-2-0.5599εt-3-0.6156εt-4-0.3034εt-5-0.2258εt-6
+0.8682εt-7-0.0106εt-8
对ARIMA(10,1,8)模型进行残差检验,符合要求,并对晴天预测日的光伏发电输出功率进行预测。
2.1.3预测结果
预测出来的数据进行反差分得到结果。如图7所示:

图7 相似日样本晴天光伏发电预测结果
为了对预测效果进行比对,本节采用没有相似日时的样本进行预测,预测结果如图8所示:
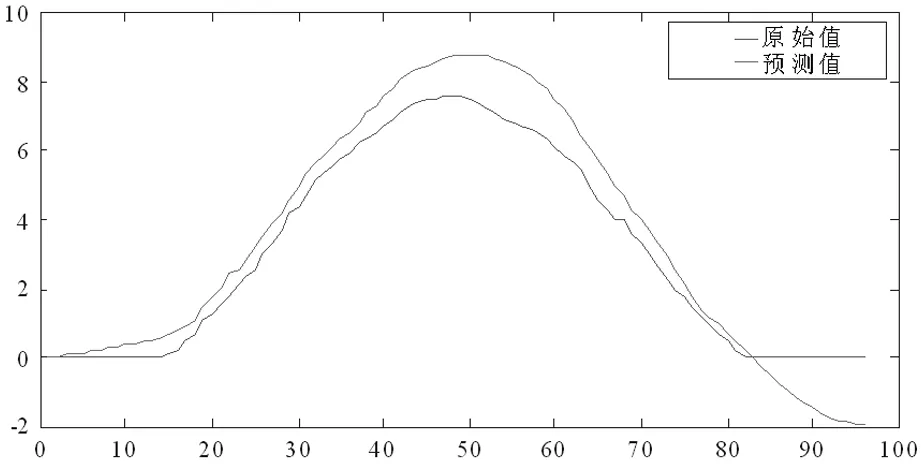
图8 未相似日样本晴天光伏发电预测结果
从图7和图8可以清楚的看出基于相似日的时间序列预测精度较高,利用平均绝对百分比误差MAPE来作为模型的评价指标,可算出未采用相似日样本的MAPE的值为18.12%,而采用相似日样本的预测误差为7.77%。
2.2 阴天情况下出力预测过程及结果分析
过程同上,对数据进行平稳性检验,对不平稳的数据进行差分,直到平稳为止,然后根据AIC准则(Akaike information criterion)对ARIMA(p,1,q)模型定阶。表2为挑选出的几种AIC最小的模型。根据AIC准则选取出最适当的阶数p为5,q为9。建立ARIMA(5,1,9)模型,所得模型为:
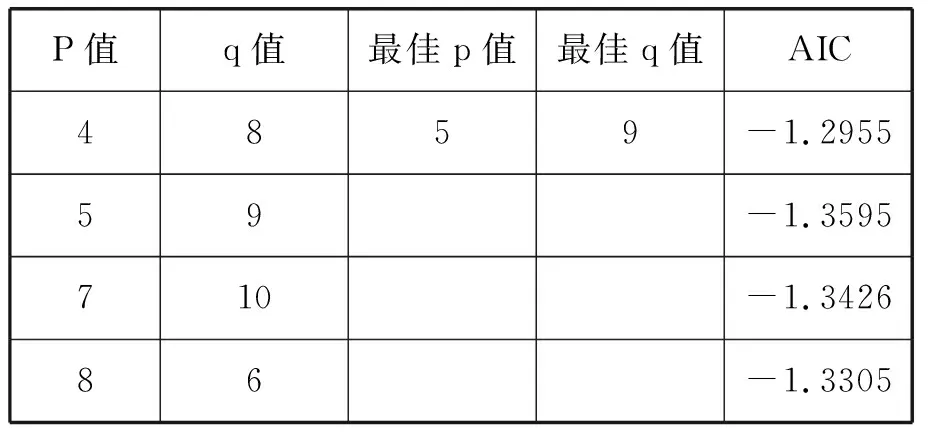
表2 阴天ARIMA模型pq值的选择
yt-1.0467yt-1+0.1548yt-2+0.4277yt-3+0.6883yt-4+0.5684yt-5yt-1.0467yt-1-0.5148yt-2+0.4277yt-3
+0.6883yt-4+0.5684yt-5=εt+0.0117εt-1-0.5890εt-2
-0.8420εt-3-0.0516εt-4+0.2379εt-5+0.5471εt-6
-0.1145εt-7-0.1868εt-8-0.0128εt-9
对ARIMA(5,1,9)模型进行残差检验,符合要求,对预测日为阴天类型的光伏发电输出功率进行预测。预测出来的数据进行反差分得到结果。如图9所示:
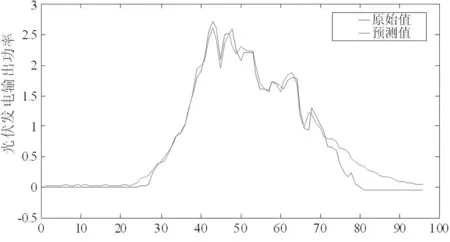
图9 相似日样本阴天光伏发电预测结果
同样,为了说明相似日的有效性,对阴天情况未采用相似日样本进行预测,结果如图10所示:

图10 未相似日样本阴天光伏发电预测结果
通过两图对比,相似日样本下的预测模型精度较高。通过式5计算出阴天的预测结果误差MPAE为19.54%,而采用相似日样本后阴天预测结果误差为8.19%,由此可见经过相似日选取的样本数据预测结果更加准确。
3 预测模型对比
为了验证时间序列ARIMA模型的有效性,本文采用灰色模型[6]与之进行对比。结果如图11所示。由于篇幅有限,仅显示阴天情况下的预测结果。

图11 灰色模型光伏发电预测结果
经过计算灰色模型预测结果的误差为27.73%;所以最终选用ARIMA模型预测更加准确。
4 结论
本文采用基于时间序列对光伏输出功率进行预测,可得到以下结论:
(1)采用相似日样本,可有效提升预测精度。
(2)采用ARIMA模型对光伏出力预测较灰色模型预测精度高。
(3)基于时间序列的ARIMA模型能对光伏出力进行有效预测。
