考虑桩土作用的桥墩受船舶撞击动力响应分析

吉 喆，岳凯乐，王贵春

(郑州大学 土木工程学院 河南 郑州 450001)

0 引 言

船桥碰撞所造成的影响是在极短时间内因船舶撞击桥墩而产生的一种非线性动态过程[1-3]。学者对船桥碰撞问题进行了一定的研究，并给出了碰撞力计算经验公式[4-5]，各国的公路与铁路桥梁设计规范也分别规定了船撞力大小的设计值[6-8]。但船桥碰撞问题十分复杂，深入研究桥梁受船舶撞击的动力响应具有重要的理论价值和现实意义。文献[9]从船舶类型角度出发，研究了桥梁结构响应的差异及原因，并与国内外规范进行了对比分析。文献[10]从船舶吨位角度出发，对万州长江大桥船撞倒坍概率进行了研究，并提出了合理的防撞措施。以上研究在有限元建模时均未考虑桩土作用的影响。随着航运水平的提高，大吨位船舶的出现加之大型桥梁的兴建，考虑桩土作用对于研究船桥碰撞问题是非常必要的。目前使用有限元方法[11]解决船桥碰撞问题时经常使用假想嵌固点法[12]、等效弹簧法[13]、有限域土体法[14]，这3种模拟桩土作用的方法在建模方式上大不相同，桥梁及船舶的动力响应也往往有明显差别。因此，在使用有限元法研究船桥碰撞问题时如何模拟桩土作用的影响也至关重要。本文使用有限元软件ANSYS/LS-DYNA，以南京长江三桥为背景分别建立不考虑桩土作用的承台底固结模型，以及考虑桩土作用的嵌固端模型、等效弹簧法模型和有限域土体法模型，分析了桩土作用对桥梁船撞响应的影响，研究了船撞过程中桥墩易损部位的动力响应，可为桥梁防撞设计及桥梁损伤分析提供参考。

1 数值模拟方法

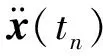
采用集中质量矩阵的动力方程组是解耦的，按照中心差分法计算时无须进行平衡迭代，后一时间步响应可通过前一时间步响应的结果计算得到。因此，这种方法是一种显式计算方法。尽管显式计算方法无须进行平衡迭代，但这种方法在计算过程中仍然无法保证完全稳定。为保证碰撞系统控制方程计算的稳定性，LS-DYNA 3D采用变步长积分法，当积分步长小于临界步长时，每一时刻的积分步才能保持稳定。一般情况下，对于船桥碰撞系统，临界积分步长的计算公式为Δte=a(le/c)，式中：Δte为单元e的临界积分步长；a为时间步长缩放因子，缺省时为0.9；le为单元e的特征长度，c为材料的声速，le/c表示一个弹性应力波传过单元e的时间。

2 船桥碰撞分析模型

2.1 主塔有限元模型

考虑到航运实际情况和该流域船桥碰撞事故多发的特点，选取南京长江三桥北主墩进行有限元建模。北主墩墩基为哑铃型圆形桩承台，宽29 m，高12 m，总长为84 m。塔墩处河床高程为-9 m。图1为南京长江三桥总体布置图，北主墩位于图中左侧。采用整体式桥墩建模，假设预应力筋和普通钢筋均匀分布在桥墩中，通过增加混凝土材料的弹性模量来考虑桥墩中钢筋的作用。主塔以实际尺寸建模，塔高215 m，建模时采用SOLID164单元，材料选取LS-DYNA中的HJC混凝土材料模型。主塔有限元模型如图2所示。如果不考虑桩土作用，则将主塔底部承台底面进行固结约束，此模型为不考虑桩土作用的承台底固结模型。

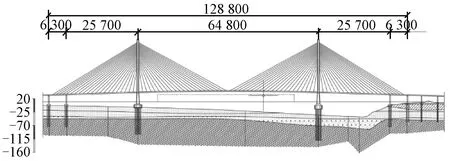
图1 南京长江三桥总体布置图(单位：cm)Figure 1 General layout of Nanjing No.3 Yangtze river bridge (unit: cm)

图2 主塔有限元模型Figure 2 Finite element model of main tower

2.2 考虑桩土作用的桥塔有限元模型

在进行船桥碰撞有限元模拟时，桩土作用是不可忽视的影响因素。采用3种方法对桥墩桩土作用进行模拟，在模拟过程中均需要建立桩的有限元模型，桩半径为1.5 m，实际桩长为88 m，对这3种桩土模型分述如下。

2.2.1假想嵌固点法有限元模型 假想嵌固点法是模拟桩土作用常用的方法之一，其将群桩基础在一定深度处固结，桩周不加任何约束。在桩仅承受水平作用力时，此方法是模拟桩土作用最为直接便利的途径。该方法建模简单且考虑了桩土之间的作用，但模拟结果的准确性往往由固结深度控制。通常选用3倍、5倍和8倍桩径长度作为桩底固结深度，分析嵌固点深度对模拟效果的影响。嵌固端有限元模型如图3所示。

2.2.2等效弹簧法有限元模型 等效弹簧法是一种较为成熟的模拟桩土作用的方法，其将桩周土体视作一系列的弹簧，通过弹簧的约束模拟桩土作用。本模型桩长为88 m，每隔8 m布设一组弹簧，弹簧的布置和等效弹簧法模型如图4所示。桩周弹簧的弹簧刚度由m法确定，等效弹簧刚度的计算公式为K=mzb0h0，式中：K为等效弹簧刚度；z为弹簧布置深度；b0为桩的等效宽度；h0为划分单元的高度；m值由桩所处地质条件确定。经查阅相关地质资料，最终确定每层弹簧的弹簧刚度。

2.2.3有限域土体法有限元模型 有限域土体法是一种模拟桩土作用较为精确的方法，其对桩周实际土体进行建模，通过有效设置桩土之间接触关系来模拟桩土之间的作用。虽然使用有限域土体法进行船桥碰撞模拟更贴近于实际，但是由于土体体积庞大，划分网格之后会产生极多的单元，大大增加了计算成本。建模时土体模型采用SOLID164单元，材料选用LS-DYNA中的D-P土体材料模型。为保证计算的准确性，根据相关地质资料，土体模型底部高程为-39 m，在这之下则为较坚硬的风化泥岩。有限域土体法有限元模型如图5所示。选用面面侵蚀接触定义土体与桩之间的接触，桩与土体之间的摩擦系数由土体性质和桩表面摩擦系数共同确定，本文中有限域土体法模型的桩周土体为沙土。通常情况下，混凝土桩与沙土之间的摩擦系数为0.35～0.50，本文在设置接触时选用的桩土摩擦系数为0.45。

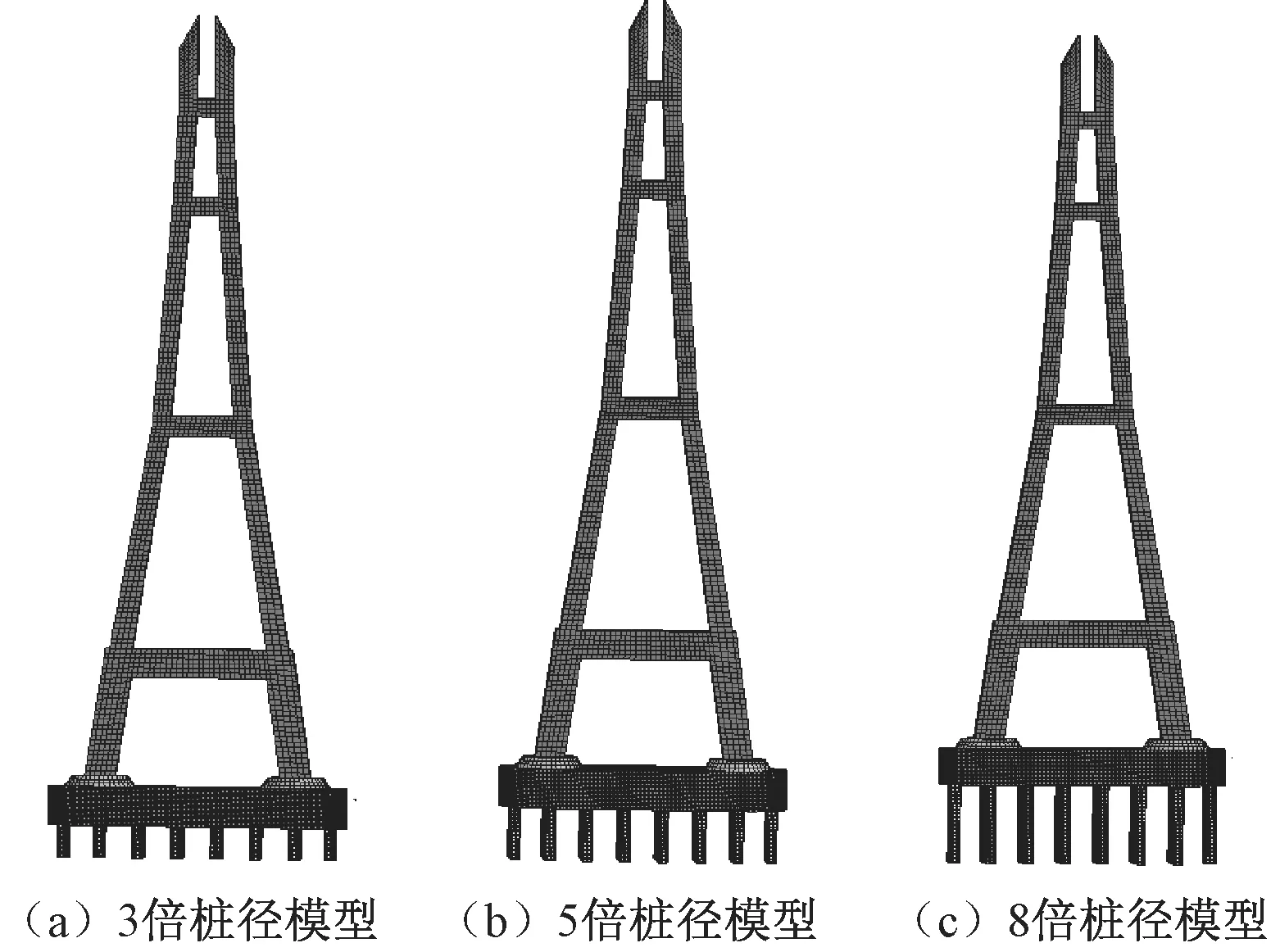
图3 嵌固端有限元模型Figure 3 Finite element model of fixed method

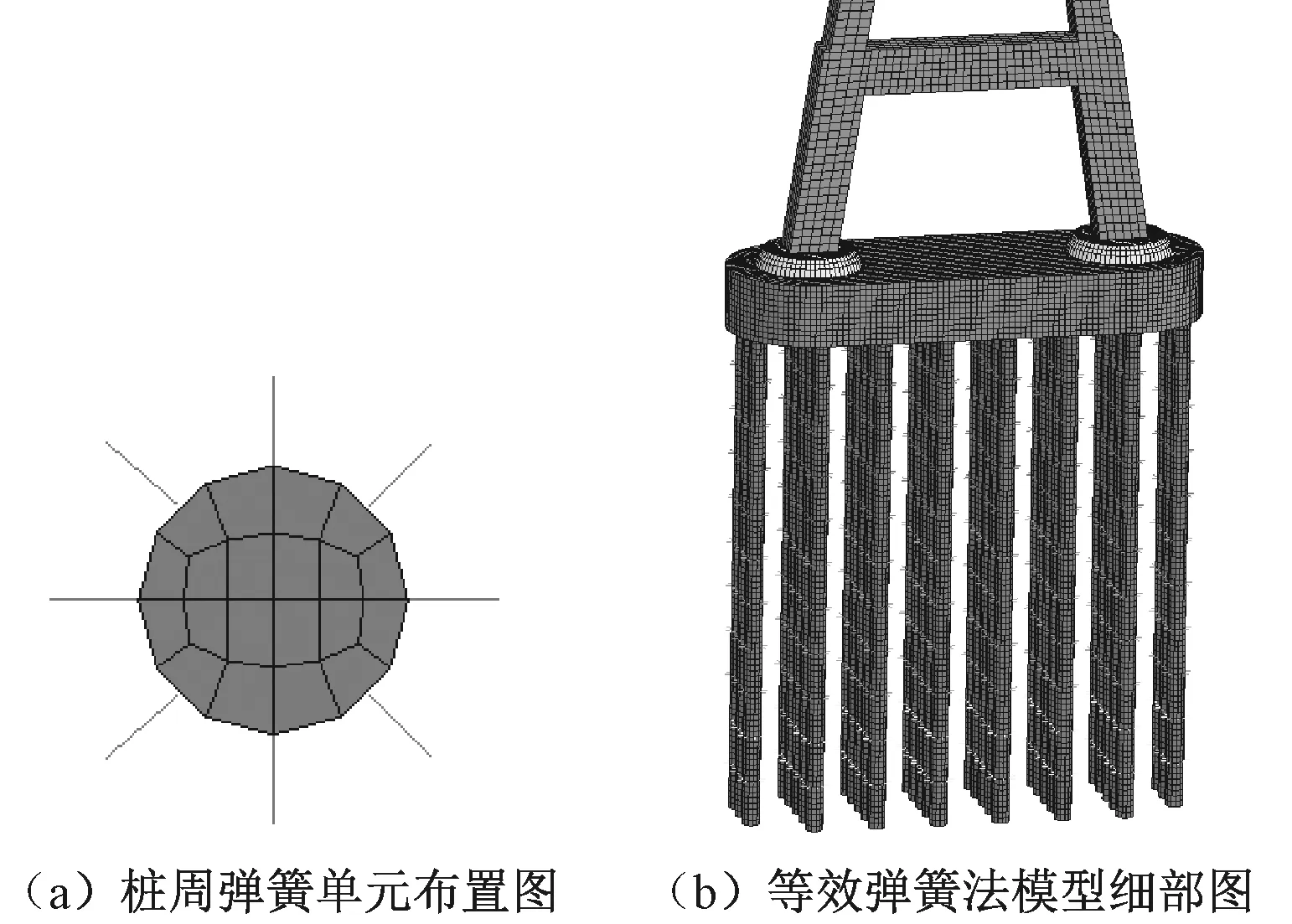
图4 等效弹簧法有限元模型Figure 4 Finite element model of equivalent spring method

2.3 船舶有限元模型

根据南京长江三桥所处流域的通航水平和航道情况，以一艘2000DWT级内河散货船为背景建立船舶模型。其总长为88.5 m，型宽为13.3 m，型深为9.4 m。在建立有限元模型时，船舶整体使用SHELL163单元，材料选用LS-DYNA中的KINEMATIC钢材材料模型。在划分网格时将船舶分为船艏和船体两部分，考虑到实际船艏结构的特点，又在船艏增设两层甲板。船桥碰撞有限元模型如图6所示。

图5 有限域土体法有限元模型Figure 5 Finite element model of finite domain soil method

图6 船桥碰撞有限元模型Figure 6 Finite element model of ship bridge collision

3 船桥碰撞动力响应分析

在计算过程中，不同的初始设置往往会导致计算结果有较大差别，如未指明，本次模拟中船舶质量为2 000 t，船艏厚度为0.02 m，船舶初速度为5 m/s，船舶沿横桥向行驶并正碰桥墩，水位高度为设计水位。

3.1 桩土作用对船桥碰撞动力响应的影响

桥梁受船舶撞击的动力响应可通过后处理软件LS-PrePost提取得到。图7给出了利用承台底固结模型、嵌固端模型、等效弹簧法模型和有限域土体法模型计算的撞击力时程曲线。可以看出，碰撞力产生的初始时刻均在0.38 s，随着碰撞的持续，碰撞力陡然加大，这些模型均在0.5 s左右产生最大碰撞力。等效弹簧法模型的撞击力最大，为45.7 MN；有限域土体法模型的撞击力为45.4 MN；3倍、5倍、8倍桩径模型的撞击力依次减小，分别为45.5 MN、45.2 MN和44.9 MN；而不考虑桩土作用的承台底固结模型的撞击力仅为37.3 MN。碰撞力在达到峰值之后会迅速减小，桩土作用模型的碰撞力均在1.06 s左右消失，而承台底固结模型的碰撞力则在1.28 s消失。仅从碰撞时长来看，承台底固结模型的碰撞持续时长明显大于桩土作用模型的碰撞时长。图8为不同模型在船舶撞击过程中的船艏变形能时程曲线。可以看出，承台底固结模型的船艏变形能远大于其他几种模型，这也解释了采用承台底固结模型时，碰撞持续时长和撞击力大小与其他几种桩土模型有较大差异的原因。在船舶与桥墩碰撞过程中，由于不考虑桩土作用的模型是将承台底部直接固结，船舶与桥墩碰撞更类似于船舶与刚性墙的碰撞，船艏相对于其他模型会产生更大的变形，船艏变形所消耗的能量会更多，因此在整个碰撞过程中碰撞力也会相应减小。

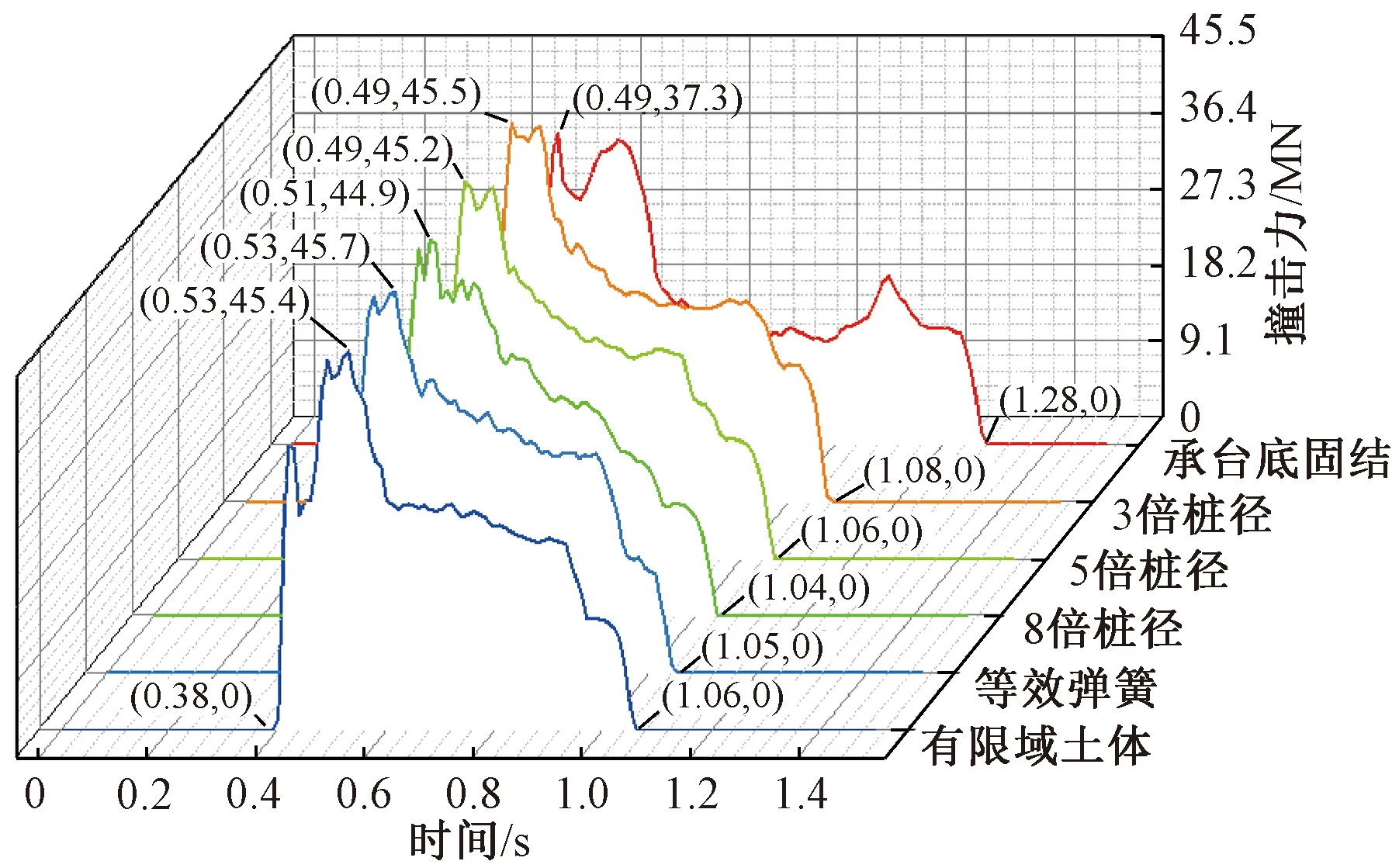
图7 撞击力时程曲线Figure 7 Time history curves of impact forces

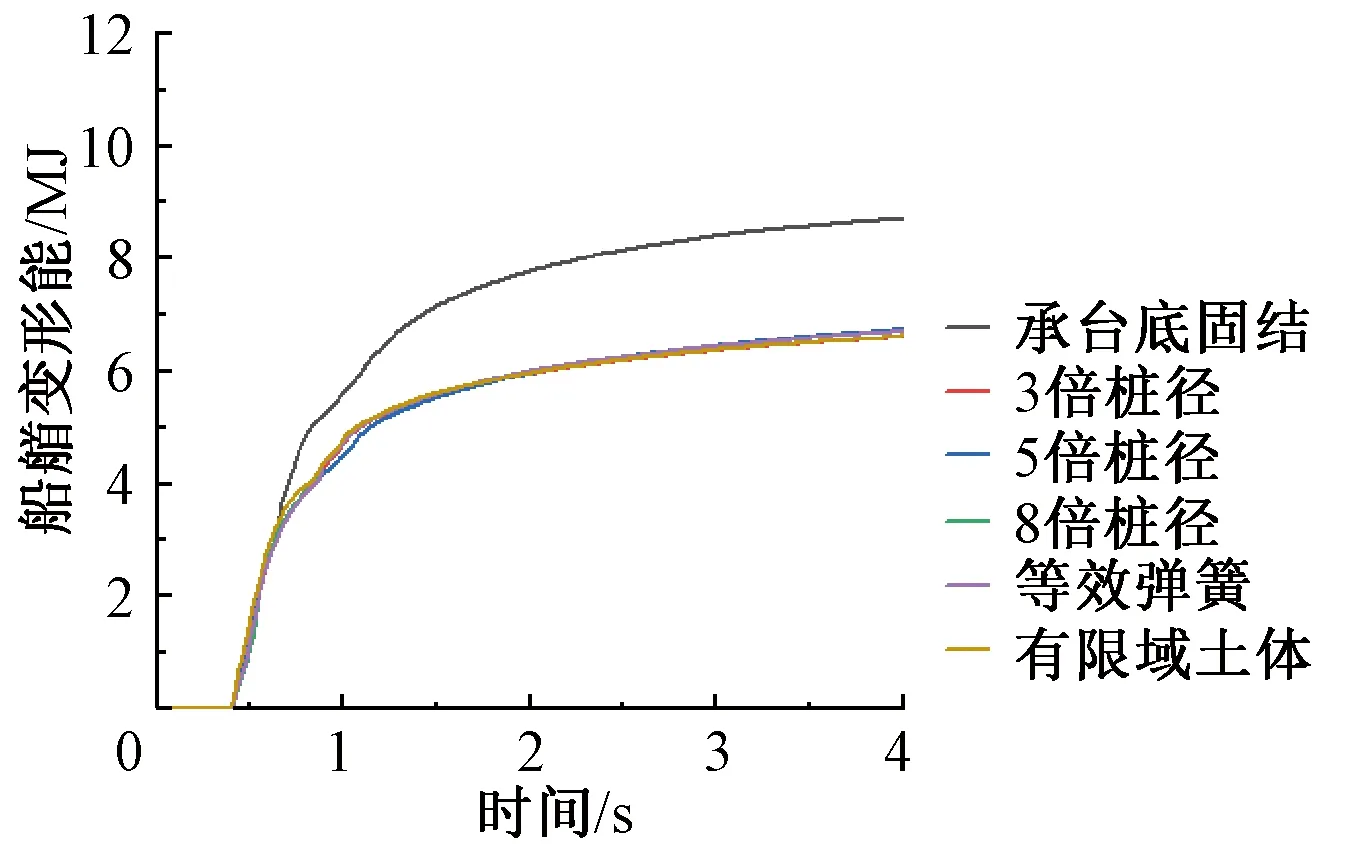
图8 船艏变形能时程曲线Figure 8 Time history curves of bow deformation energy

图9和图10分别为承台顶部横桥向和纵桥向位移时程曲线。由图9可知，承台底固结模型墩台顶部的最大横桥向位移为0.34 mm；3倍、5倍、8倍桩径模型的值分别为3.24 mm、9.01 mm和20.19 mm；等效弹簧法模型的值为27.92 mm；有限域土体法模型的值为18.50 mm。就横桥向位移来看，承台底固结模型的计算位移峰值与桩土作用模型完全不在一个数量级，8倍桩径模型的最大横桥向位移与等效弹簧法模型和有限域土体法模型的情况接近。3倍和5倍桩径模型的墩顶振动频率较大，等效弹簧法模型的墩顶振动频率较小，8倍桩径模型和有限域土体法模型的情况则基本一致。由图10可知，承台顶部纵桥向位移与横桥向位移具有相似规律。不同的是，由5倍桩径模型与等效弹簧法模型得到的承台顶部纵桥向位移相对较大，分别为4.43 mm和3.19 mm，由3倍桩径、8倍桩径和有限域土体法模型得到的承台顶部纵桥向位移较小，分别为2.35 mm、1.32 mm和1.04 mm，而由承台底固结模型得到的位移结果仅为0.02 mm。由承台顶部横桥向和纵桥向位移时程曲线可知，在船桥碰撞过程中，不考虑桩土作用得到的桥梁响应往往远小于实际情况，尤其是在桥梁上部结构。综上所述，在进行桥梁船撞分析时，如果不考虑桩土作用的影响，船撞力的计算结果偏小，而桩土作用模型计算的撞击力约为承台底固结模型计算值的1.22倍；不考虑桩土作用的模型的船撞持续时长偏大，桥梁的响应则远远小于桩土作用模型的计算结果。因此，桩土作用是船桥碰撞分析中不可忽视的影响因素。

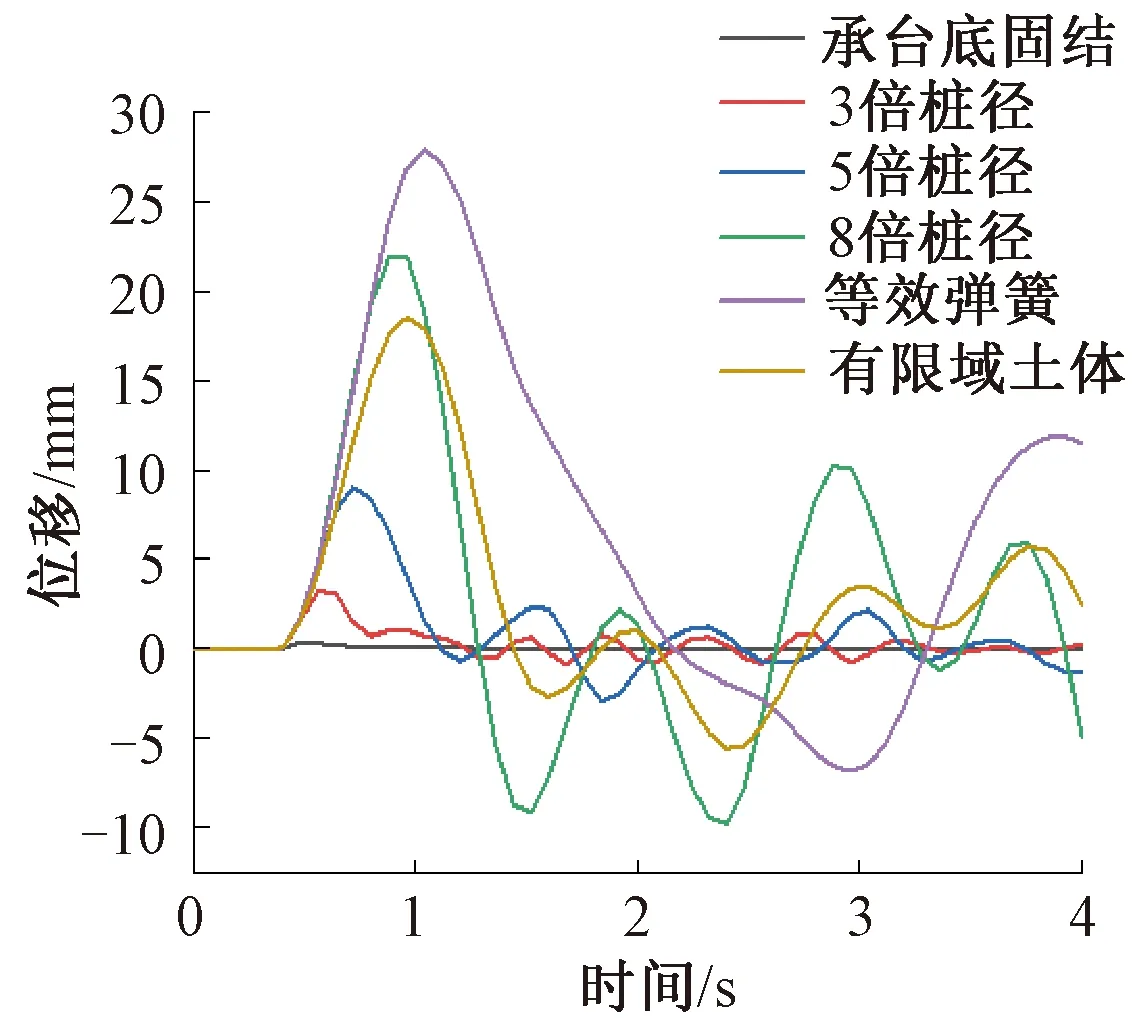
图9 承台顶部横桥向位移时程曲线Figure 9 Time history curves of transverse displacements at the top of pier

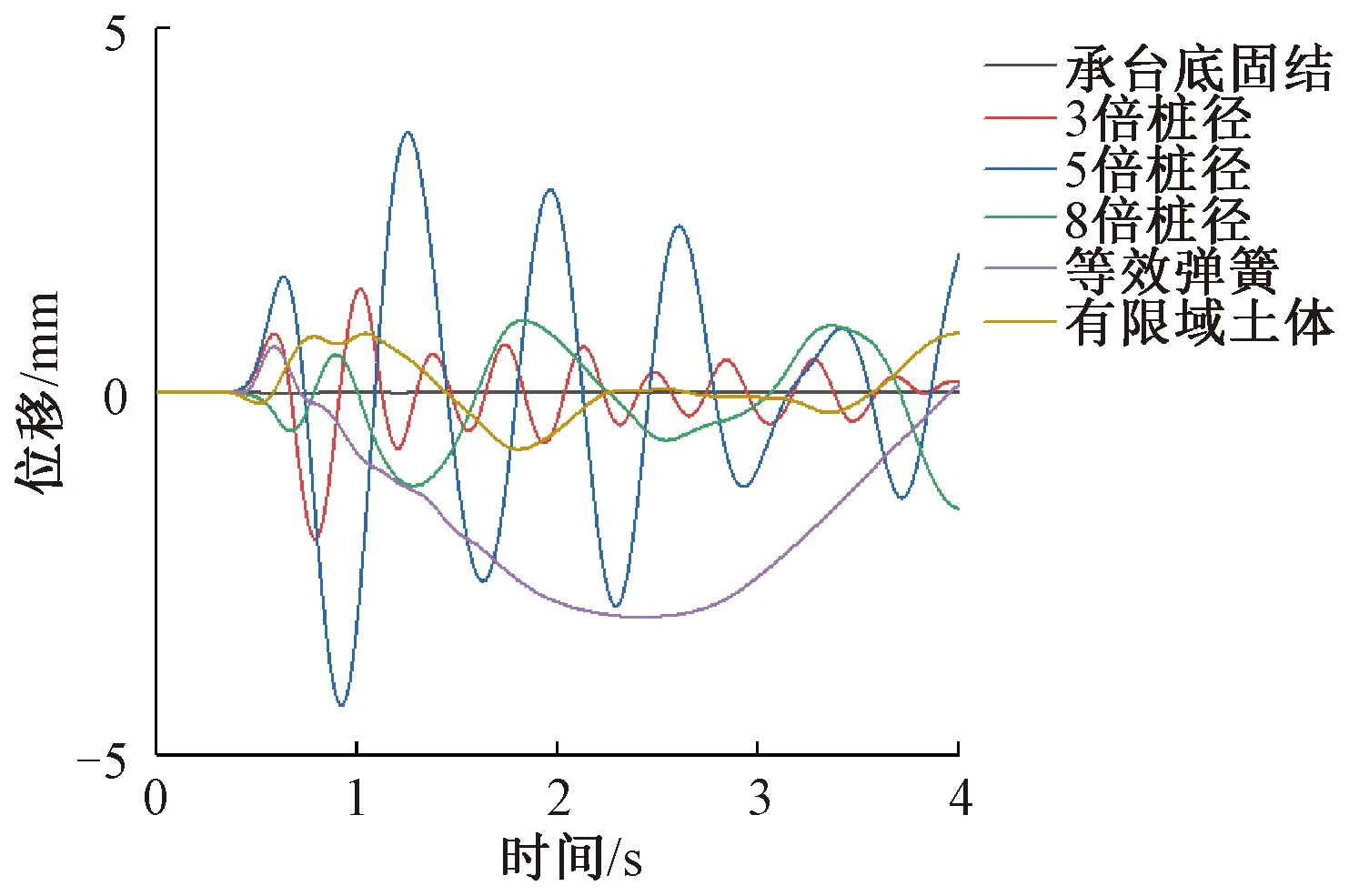
图10 承台顶部纵桥向位移时程曲线Figure 10 Time history curves of longitudinal displacements at the top of pier

3.2 桩土模型对比分析

在船桥碰撞有限元模拟过程中，由于建模方式的不同，桥墩在不同桩土模型下所得到的动力响应也有所不同。在上述计算结果的基础上，进一步分析不同桩土模型计算的桥墩动力响应的差别。图11为8倍桩径模型在0.40 s、0.64 s、0.80 s和1.12 s的桥墩Mises应力云图。可以看出，图11(a)中船桥刚刚发生碰撞，应力集中产生在承台被撞击部位。随着撞击的持续，由图11(b)和(c)可见，桩顶和桩底应力逐渐增大。图11(d)中船桥碰撞已经结束，桩顶和桩底产生很大的应力，桥墩上部结构也产生一定应力。显然，桥墩产生较大应力处位于桩顶，因此船桥碰撞过程中桥梁最易发生损坏的部位在桩顶与承台相接处。

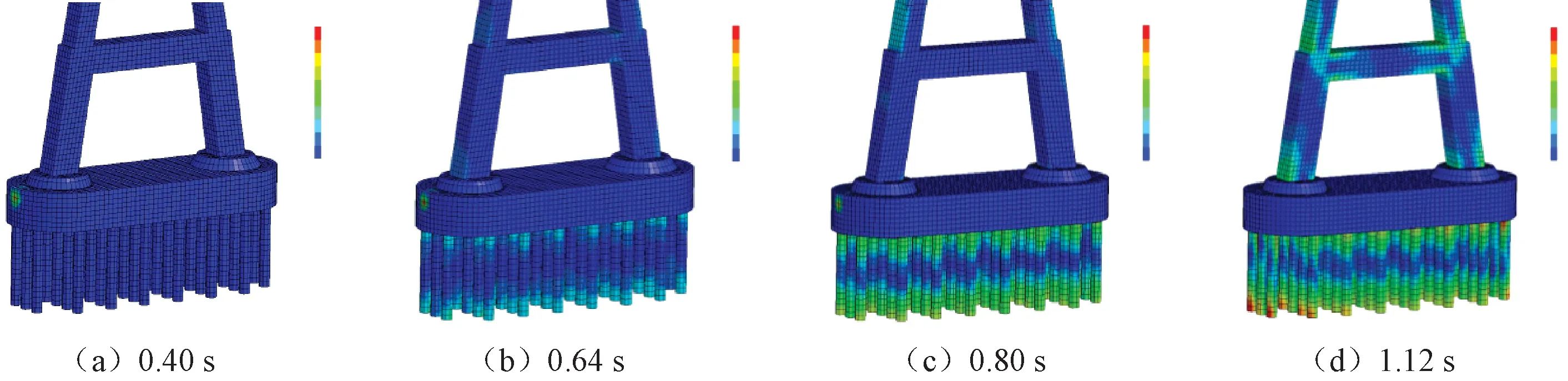
图11 桥墩在不同时刻的应力云图Figure 11 Stress contours of pier at different moments

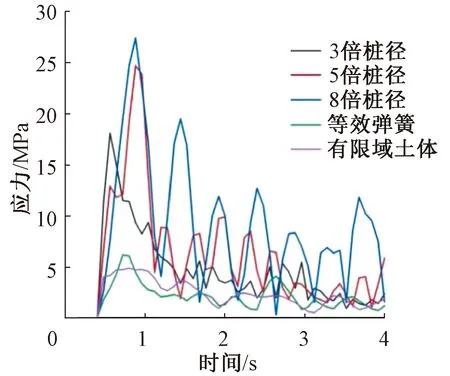
图12 桩顶应力时程曲线Figure 12 Time history curves of pile top stresses

由于桥墩受船舶撞击后应力集中产生在桩顶位置，故提取由不同桩土模型计算的桩顶应力进行对比分析。图12为不同桩土模型的桩顶应力时程曲线。可以看出，嵌固端模型的桩顶应力相对较大，3倍、5倍、8倍桩径模型的桩顶应力峰值分别为18.1 MPa、24.7 MPa和27.4 MPa，而等效弹簧法模型和有限域土体法模型的桩顶应力峰值较小，分别为6.16 MPa和4.73 MPa。产生这种差别的原因是嵌固端模型仅将桩在一定深度处固结，桩周围没有设置任何约束，而等效弹簧法模型和有限域土体法模型的桩周都有相应的约束存在。因此，应用嵌固端模型，桩顶和桩底产生的应力相对较大。如果进行桩顶应力分析，采用等效弹簧法模型和有限域土体法模型得到的计算结果更加准确。

在计算过程中使用不同桩土模拟方法，桩的受力情况也会有差别。由图11可见，在船桥碰撞过程中，采用嵌固端模型，每一根桩的受力情况几乎相同，而这种受力状态也出现在等效弹簧法模型中。有限域土体法模型中桩的受力情况则与这2种桩土模型不一致，图13为有限域土体法模型在0.48 s、0.88 s和1.52 s的土体Mises应力云图。由图13(a)可见，从左至右前两列和后两列桩周土体产生的应力明显大于中间两列桩周土体的应力。由图13(b)和(c)可见，内侧桩周土体的应力明显小于外侧桩周土体的应力。由此可知，由于桩周边界条件的不同，有限域土体法模型中桩的受力情况与嵌固端模型和等效弹簧法模型有一定差别，由有限域土体法模型得到的计算结果更贴近于实际情况。

图13 土体在不同时刻的应力云图Figure 13 Stress contours of soil at different moments

在分析桩土作用的桥墩动力响应时，计算桩顶的位移时程也是十分有意义的。与承台顶部位移时程曲线相似，可通过有限元软件提取出不同桩土模型桩顶纵桥向和横桥向的位移时程曲线。由于曲线趋势与图9和图10几乎一致，仅在数值上有所差异，所以本文不再给出桩顶的位移时程曲线。

为了更直观地对比不同桩土模型数值模拟结果之间的差异，将不同模型的计算结果汇总于表1。可以看出，嵌固端模型、等效弹簧法模型和有限域土体法模型计算所得撞击力大小和撞击时长基本一致。使用3倍和5倍桩径模型计算，其撞击力峰值在0.49 s时发生；使用等效弹簧法和有限域土体法模型计算，其撞击力峰值在0.53 s时发生。不同模型的承台顶部和桩顶的横桥向位移差别较大。使用3倍和5倍桩径模型时承台顶部横桥向位移较小，分别为3.24 mm和9.01 mm，使用8倍桩径模型时其值为20.19 mm，分别增大了5.23倍和1.24倍；由8倍桩径模型得到的横桥向位移与由其他2种桩土模型得到的横桥向位移差别不大。由不同模型得到的承台顶部和桩顶的纵桥向位移也有差别，其中8倍桩径模型与有限域土体法模型的计算结果相近。3倍、5倍、8倍桩径模型和等效弹簧法模型计算的桩顶应力分别为有限域土体法模型计算值的3.85倍、5.25倍、5.83倍和1.31倍，这种因使用不同桩土模型而产生的较大桩顶应力差异与桩周边界条件有密切关系。

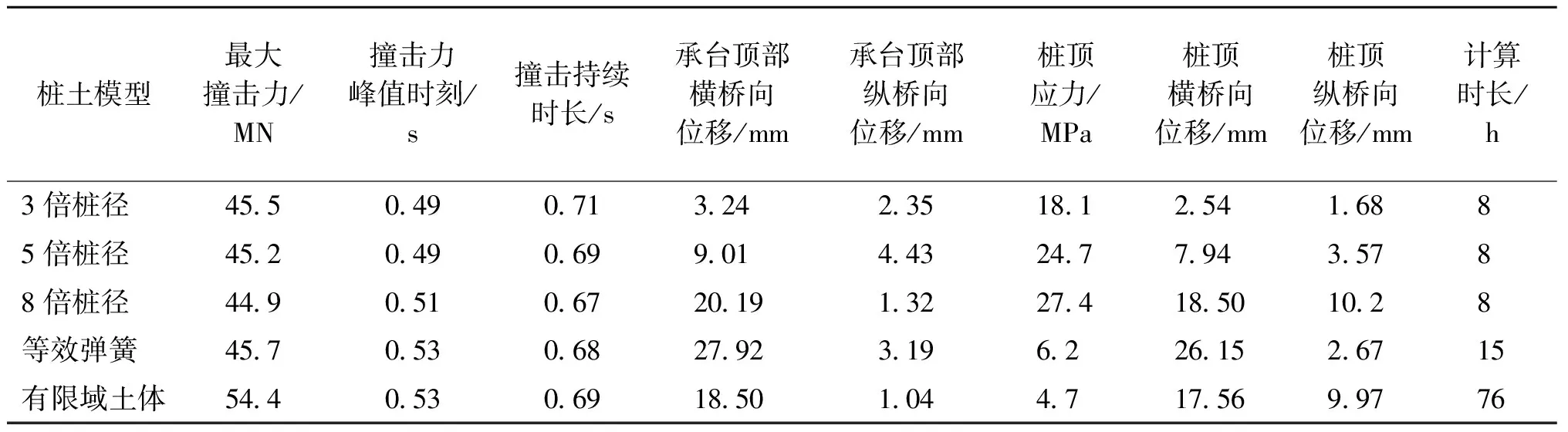
表1 不同模型的计算结果对比Table 1 Comparison of calculation results by different models

在进行船桥碰撞数值模拟过程中，有限域土体法的计算时长远超过其他2种方法，但该模型是考虑桩土作用计算桥墩船撞响应最为精确的方法。综合来看，就所研究的桥墩而言，如果仅计算撞击力大小和桥墩位移变化，8倍桩径模型与其他2种桩土模型计算结果的吻合度较高。因此，假想嵌固点法中的8倍桩径模型更适合于本桥墩的模拟，如果为了节约计算成本且不考虑桩的响应，嵌固端模型不失为一种有效的桩土作用模型。此外，等效弹簧法模型也是考虑桩土作用计算船桥碰撞动力响应较为精确的方法。

4 结论

通过数值模拟分析船桥碰撞问题，桩土作用是不可忽视的影响因素之一。不考虑桩土作用所得到的桥梁动力响应往往偏小，在实际工程项目计算中可能会造成重大偏差。用不同桩土模型计算所得的桥梁船撞动力响应有所不同，墩台顶部位移和桩顶位移也有差异，其中由8倍桩径模型得到的结果与由其他2种模型计算所得结果的吻合度较高。由嵌固端模型计算所得的桩顶应力与由其他2种方法得到的结果相差较大，并且由嵌固端模型与等效弹簧法模型得到的桩的动力响应与由有限域土体法模型得到的结果也有所差异。有限域土体法模型内侧桩受力情况往往小于外侧桩，而由其他2种方法计算的桩的受力情况近乎一致。就本桥墩而言，在使用假想嵌固点法建模时，推荐使用8倍桩径模型。在使用有限域土体法模型计算时，计算时长是模拟过程中需要考虑的因素，但该模型的计算精度最高。等效弹簧法模型计算简便且模拟效果较好，也是一种较为有效的桩土作用模型。