随机微分方程平衡θ-Heun法的收敛性
2020-11-18康红喜张引娣
康红喜,张引娣,蒋 茜
(长安大学 理学院 陕西 西安 710064)
0 引言
随机微分方程由于能够很好地描述各种事物的客观现象,所以被广泛应用于各个领域。为了能够更加准确地解释说明各种客观现象,学者们先后研究出了许多数值方法。收敛性与稳定性是研究一个新数值方法的主要对象,它们能够评判一个数值方法是否有效。文献[1-6]分别研究了Euler法、Milstein法的收敛性。另外Heun方法[7]和全隐式的平衡方法[8]也是求解随机微分方程的有效方法。θ-Heun方法[9]是在Heun方法的基础上改进得到的。本研究对θ-Heun方法进行改进,构造一种新的Heun方法,即平衡θ-Heun方法,并研究用这种新方法求解随机微分方程的收敛性。
1 随机微分方程与数值方法
1.1 随机微分方程
(1)
其中:t∈[0,T];x∈Rd,称函数f(x)为漂流项,函数g(x)为扩散项,二者在[0,T]上都是连续可测的,且有E|x0|2<∞;随机过程W(t)是滤过概率空间(Ω,F,{Ft}t≥0,P)上的标准布朗运动,当t>0,步长h>0时,其增量ΔW(t)=W(t+h)-W(t)独立于{Ft},因此有ΔW(t)~N(0,h)。
1.2 数值方法
定义1求解方程(1)的θ-Heun方法[9]为
Xn+1=Xn+(1-θ)f(Xn)h+g(Xn)ΔWn+θf(Xn+hf(Xn))h,
(2)
在这个方法的基础上结合平衡法的思想,构造出一种新的Heun法,即平衡θ-Heun方法。
定义2称
Xn+1=Xn+(1-θ)f(Xn)h+g(Xn)ΔWn+θf(Xn+hf(Xn))h+Cn(Xn)(Xn-Xn+1)
(3)
为求解随机微分方程(1)的平衡θ-Heun方法,当θ=0时,方法(3)即为平衡法。式(3)中Cn(Xn)=C0(tn,Xn)h+C1(tn,Xn)|ΔWn|,记C0(X)=C0,C1(X)=C1,控制函数C0、C1为d×d的实值矩阵,满足可逆矩阵
M(t,X)=I+α0C0(t,X)+α1C1(t,X),
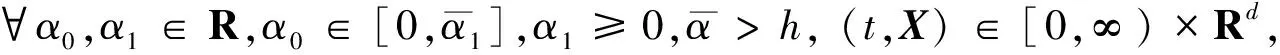
在本文中我们记x(tn)是方程(1)在tn处的精确值,Xn是用平衡θ-Heun方法在tn处求得方程(1)解的近似值,X(tn+1)是用平衡θ-Heun方法在x(tn)处进行一步迭代得到的近似解。
2 平衡θ-Heun方法的收敛性
定义3[11]记平衡θ-Heun方法的局部误差为δn+1=x(tn+1)-X(tn+1),n=0,1,2,…,N-1。全局误差为εn=x(tn)-Xn,n=1,2,…,N-1。
定义4[12]若存在正常数C(C与h无关),当h→0有
则称p1、p2、p分别为数值方法在均值意义下局部收敛阶、均方意义下局部收敛阶、均方强收敛阶。
引理1[13]如果f(x)、g(x)满足条件
(i) Lipschitz条件:对任意的x,y∈Rd,存在常数L1>0,使得
|f(x)-f(y)|2∨|g(x)-g(y)|2≤L1|x-y|2;(ii) 线性增长条件:对任意的x∈Rd,存在常数L2>0,使得
|f(x)|2∨|g(x)|2≤L2(1+|x|2)或|f(x)|∨|g(x)|≤L2(1+|x|);
那么方程(1)满足性质
(ii)∀t0≤s≤t≤T,有E|x(t)-x(s)|2≤c(t-s),c>0。
2.1 均值、均方相容阶
定理1如果方程(1)满足引理1的(i)和(ii),矩阵函数M(x)可逆且满足|M(x)|≤K,假设矩阵函数C0、C1各分量一致有界,则平衡θ-Heun法是p1=3/2阶均值相容,p2=1阶均方相容,即
其中:C是不依赖于h的常数,但是可以依赖于T和初值x0。
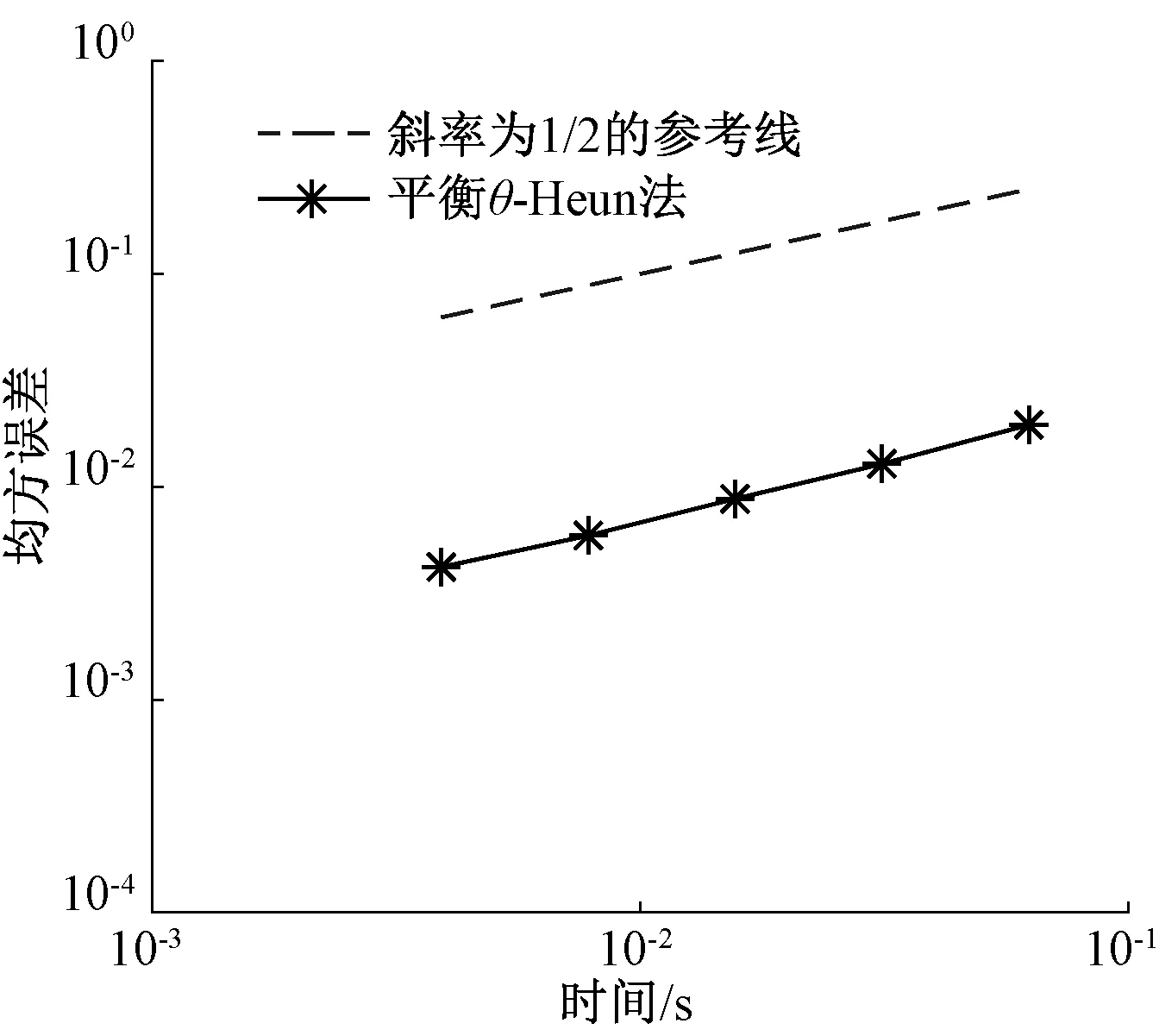
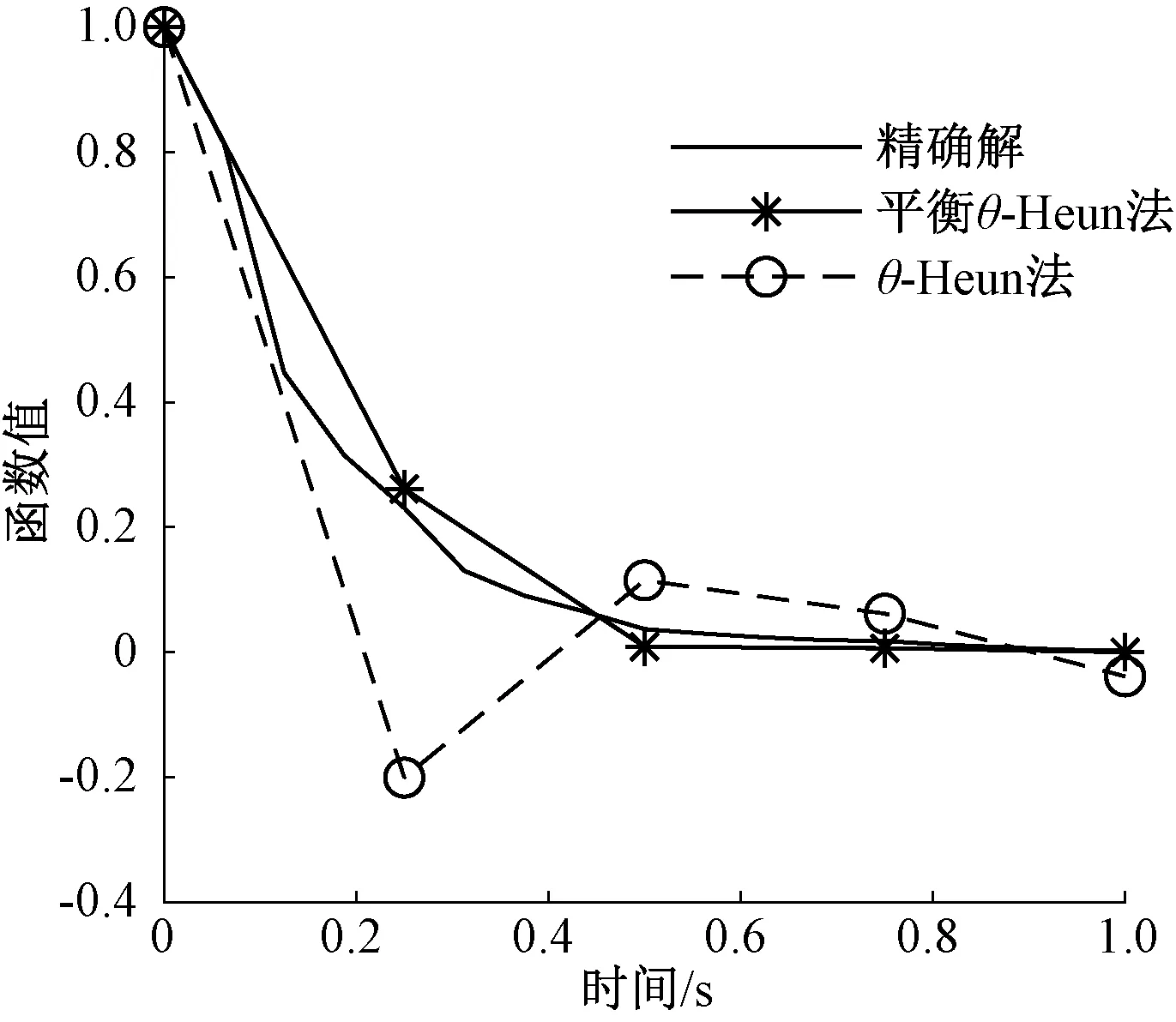
证明设0 (4) (5) 由于δn+1=x(tn+1)-XB(tn+1),再利用θ-Heun法的均值、均方相容阶定理1[9],则 |E(δn+1)|=|E(x(tn+1)-XB(tn+1))|≤|E(x(tn+1)-XH(tn+1))|+ |E(XH(tn+1)-XB(tn+1))|≤Ch2+|E(XH(tn+1)-XB(tn+1))|。 (6) 从真解x(tn)出发,对XH(tn+1),XB(tn+1) 分别经式(2)和式(3)一步计算可得 XB(tn+1)=x(tn)+(I+Cn(x(tn)))-1((1-θ)f(x(tn))h+ θf(x(tn)+hf(x(tn)))h+g(x(tn))ΔWn), (7) XH(tn+1)=x(tn)+(1-θ)f(x(tn))h+θf(x(tn)+hf(x(tn)))h+g(x(tn))ΔWn。 (8) 结合式(7)、(8)可得 XH(tn+1)-XB(tn+1)=[I-(I+Cn(x(tn)))-1]((1-θ)f(x(tn))h+θf(x(tn)+hf(x(tn)))h+ g(x(tn))ΔWn)=[(I+Cn(x(tn)))-1(I+Cn(x(tn)))-(I+Cn(x(tn)))-1]((1-θ)f(x(tn))h+ g(x(tn))ΔWn+θf(x(tn)+hf(x(tn)))h)=(I+Cn(x(tn)))-1Cn(x(tn))((1-θ)f(x(tn))h+ θf(x(tn)+hf(x(tn)))h+g(x(tn))ΔWn)。 (9) 记Cn(x(tn))=Cn,因为ΔWn与Ftn独立,所以E((I+Cn)-1Cng(x(tn))ΔWn)=0,再由|M(t,x)-1|≤K可得 |E(XH(tn+1)-XB(tn+1))|= |E(I+Cn)-1Cn((1-θ)f(x(tn))h+θf(x(tn)+hf(x(tn)))h+g(x(tn))ΔWn)|≤ Kh|E(Cn(1-θ)f(x(tn)))|+Kh|E(Cnθf(x(tn)+hf(x(tn))))|。 (10) |E(Cnθf(x(tn)+hf(x(tn))))|≤E(E(|Cnθf(x(tn)+hf(x(tn)))||Ftn))= E(|θf(x(tn)+hf(x(tn)))|E|Cn|Ftn)≤E(|f(x(tn)+hf(x(tn)))|E|C0h|+|C1||ΔWn||Ftn)≤ (11) 同理可得 |E(Cn(1-θ)f(x(tn)))|≤Ch1/2。 (12) 结合式(6)、(10)~(12)得,|E(δn+1)|≤Ch2+Ch3/2≤Ch3/2,h→0。 下面我们证明定理的第二部分。 对δn+1=x(tn+1)-XB(tn+1)两边平方并取均值,可得 E|δn+1|2=E|x(tn+1)-XB(tn+1)|2≤2E|x(tn+1)-XH(tn+1)|2+2E|XH(tn+1)-XB(tn+1)|2≤ 2Ch2+2E|XH(tn+1)-XB(tn+1)|2。 (13) 根据式(9),利用不等式(a+b+c)2≤3a2+3b2+3c2,可得 其中: E|Cnf(x(tn))h|2≤h2E(E|Cnf(x(tn))h|2|Ftn)≤2h2E(|f(x(tn))|2E(|C0|2h2+ |C1|2|ΔWn|2|Ftn))≤2L2h2(|C0|2h2+|C1|2h)E(1+|x(tn)|2)≤Ch3。 (14) 同理 E|Cnf(x(tn)+hf(x(tn)))h|2=h2E(E|Cnf(x(tn)+hf(x(tn)))|2|Ftn)≤ (15) 又E|Cng(x(tn))ΔWn|2=E(|g(x(tn))|2E(|CnΔWn|2|Ftn)),而 因此 (16) 定理2在定理1的条件下,对于方程(1)平衡θ-Heun法的均方收敛阶为1/2,即 其中:C为常数。 证明设0≤θ≤1, (17) 其中: μn=(I+Cn(x(tn)))-1((1-θ)f(x(tn))h+θf(x(tn)+hf(x(tn)))h+g(x(tn))ΔWn)- (18) 结合欧氏内积〈x,y〉=xΤy,〈x,x〉=|x|2,对式(17)两边平方并取均值可得 E|εn+1|2=E〈εn+δn+1+μn,εn+δn+1+μn〉≤ E|εn|2+2E|δn+1|2+2E|μn|2+2|E〈εn,δn+1〉|+2|E〈εn,μn〉|。 (19) 进一步计算式(18),得 (20) 为了方便讨论,令 (21) 结合式(20)、(21),可得 E|μn|2=E|An((1-θ)f(x(tn))h+θf(x(tn)+hf(x(tn)))h+g(x(tn))ΔWn)+ (22) 下面设max{|C0(x)|,|C1(x)|}≤M2,利用引理1,分别计算(22)式最后一个不等式的各项,即 6E|Anf(x(tn))h|2≤ (23) 同理可以得到 (24) 由E|ΔWn|4=3h2,则 (25) (26) (27) (28) 根据式(22)~(28),可得 E|μn|2≤Ch2+ChE|εn|2。 (29) 接下来计算式(19)的后两项,由|Eδn+1|≤Ch2及Holder不等式,可得 2(E|εn|2)1/2(E|Ch2|2)1/2≤2(hE|εn|2)1/2(h-1E|Ch2|2)1/2≤hE|εn|2+Ch3。 (30) 同理 则 2|E〈εn,μn〉|≤hE|εn|2+Ch2+ChE|εn|2≤Ch2+ChE|εn|2。 (31) 又因为E|δn+1|2≤Ch2,结合式(19)、(29)~(31),得 E|εn+1|2≤Ch2+E|εn|2+Ch2+ChE|εn|2+hE|εn|2+Ch3+Ch2+ChE|εn|2≤ (1+Ch)E|εn|2+Ch2。 (32) 对于试验方程dx(t)=-5x(t)dt+0.5x(t)dW(t),当x0=1,T=1,我们用h=Δt=2-4来模拟该方程的精确解。对于数值方法的控制参数取C0=-λ/2,C1=0以及θ=0.15时,用Matlab软件模拟平衡θ-Heun法和θ-Heun法的数值解,得到图2。通过观察图2可以知道平衡θ-Heun法的数值解与精确解逼近程度优于θ-Heun法。 图1 平衡θ-Heun法的收敛性Figure 1 Convergence of balanced θ-Heun method 图2 数值解与精确解的对比Figure 2 Comparison of numerical solution and exact solution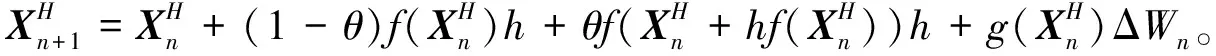
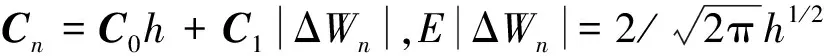
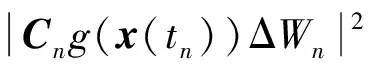
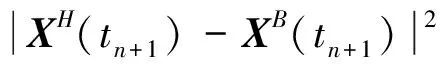
2.2 均方收敛阶
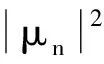
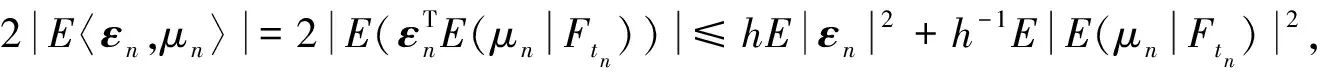
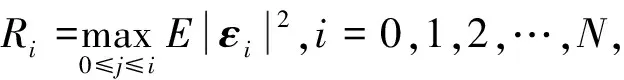
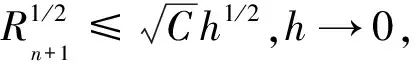
3 数值实验