巧用三角函数图像 智解水库水量变化问题
——以北半球地中海气候为例
2020-11-18山东
山东
一、问题产生背景
高中地理对气候的考查主要体现在气候类型的判读、气候特征的识记,以及气候分布的分析等。其中对地中海气候的考查在各种气候类型中占有较大比例。试题对地中海气候类型区内水库水量变化问题的考查一般较难,学生需结合地中海气候类型特点、所考查地区的南北半球分布等信息在一个动态的过程中把握地中海气候区水库水量的变化情况。通过深度研究地中海气候区水库水量变化情况,在实际教学的基础上提出较为合理的数学模型,即将一年内北半球地中海气候区水库水量盈余率/量、随月份的变化情况模拟成sin、cos函数的形式,方便学生学习记忆,有利于学生加深理解,在实际教学过程中收到良好的效果。
二、地中海气候区水库水量的考查方式
通常情况下地中海气候区水库水量的考查借助地中海气候类型的气温降水量柱状图以及水量盈余率/量进行考查。水量盈余率/量是衡量水库蓄水量变化的重要指标(水量盈余率=流入量/流出量)(水量盈余量=流入量-流出量)。而水量盈余率/量是最常见的考查方式。一般情况下水量盈余率/量有三种类型表现形式:表格法、折线图法、曲线图法(如表1、图1、图2)。

表1 水库盈余率表格表示法
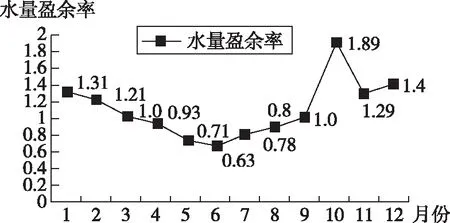
图1 水库盈余率折线图表示法
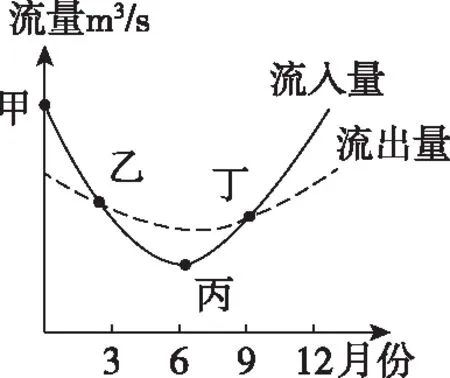
图2 水库盈余率曲线图表示法
三、sin、cos函数模型图像的拟合
1.给定某一地中海气候气温降水量示意图(如图3)
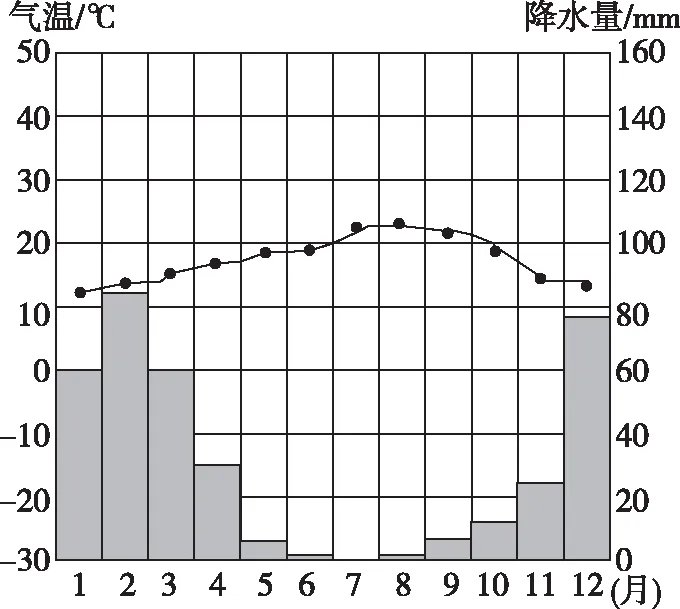
图3 地中海气候气温降水量示意图
2.将全年各月降水距平进行拟合
从图3可知地中海气候全年各月降水6—8月最少,12月—次年2月最多。由于地中海气候区水库、湖泊全年主要补给方式为大气降水,这里我们暂不考虑地下水等补给方式。这样降水量的变化情况可以与月份拟合成sin函数关系(如表2、图4),同理水库、湖泊水量盈余情况可以与时间拟合成相应的cos函数(如图4)。

表2 全年各月距平降水量与时间(月份)的拟合数据表
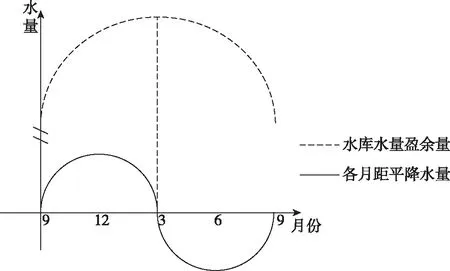
图4 北半球地中海气候区sin、cos函数模型
(全年各月距平降水量、水库水量盈余量随月份变化情况示意图)
注:水库水量盈余量为多年均值。
3.图像解析
图像分两部分,下部实线为sin函数图像;上部为cos函数图像。两者周期皆为1年。由sin函数图像可知北半球地中海气候区在冬半年(9月—次年3月)函数曲线分布在x轴上部,即在冬半年各月距平降水量数值为正,则可推知北半球地中海气候冬半年各月降水量>此气候区全年平均降水量;同理北半球地中海气候夏半年(次年3月—次年9月)各月降水量<此气候区全年平均降水量。在一个年度周期内,3月与9月距平降水量与全年平均降水量相等。由cos函数图像可知北半球地中海气候区水库水量盈余量在3月份达到一年中最大值(如图4,图中的竖直虚线所示),在9月份达到一年中的最小值。
四、sin、cos函数模型图像在解题中的应用
1.典型例题
图5是受西风季节性影响的某水库各月水量盈余率统计图。据此完成下题。
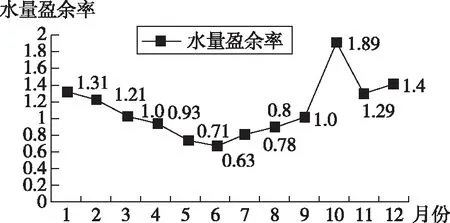
图5
推断该水库水位
( )
A.3月最高 B.6月最低
C.9月和3月一样高 D.10月最高
2.典型分析
根据数值规律发现此图表示的地点正是北半球某地中海气候区的水库,则其规律如图4所示。图4中所示水库水量盈余量即为此时水库的实际水量,对同一水库而言水量与水位呈正相关,即水量越大水位越高,水量越小水位越低。据此学生可以快速锁定答案为A。
3.应用展望
本文为方便讨论只验证了北半球地中海气候区的情况,本函数同样适用于南半球地中海气候类型区(需要将横坐标的时间都加6个月,纵坐标不变,函数图像不变)。
本函数图像作为数学内容应用到地理教学中既体现出地理学的包容性也使数学三角函数这一模块更具有生命力。将这一函数图像应用于此类问题的教学和解题,既方便学生的理解又能使学生快速掌握加深记忆。在教学过程中注意引导学生发现学科之间的联系,是现代教育提高学生核心素养、增强学生学习能力的重要体现。
