基于风速分频和权值匹配的RBF 超短期风电功率预测方法

杨 茂， 董 昊

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学）， 吉林 吉林 132012）

0 引言

由于我国能源结构的改变， 可再生能源逐渐被重视，其中风电在电网中所占的比重越来越大。当大规模风电机组并入电网时， 由于风能的不稳定性与间歇性， 当系统中风电场的装机容量占系统总负荷的比例大于某个值时， 将使整个系统无法安全平稳地运行。鉴于此，改善风电预测输出功率的精度，减小实际值与预测值之间的误差，对风电大范围并网、 实时跟踪大电网或微电网系统的调度策略以及实现其经济运行具有重要的现实意义[1]。

近年来， 国内外学者对于风电功率预测做了许多深入的研究。 文献[2]将改进的EMD 算法与支持向量机相结合，与单一的预测模型相比较，该方法在预测精度上有了很大提高。 文献[3]基于支持向量机在学习速度和泛化性能上的优势， 提出了基于支持向量机的实时风电功率模型，该模型具有更高的预测精度和泛化性能。 文献[4]通过对NWP信息进行低冗余度特征的提取，并结合神经网络，提高了预测精度。文献[5]通过径向基函数（RBF）建立了风电功率预测模型。 综上所述，RBF 神经网络学习过程收敛速度快，与其他类似网络相比，表现出快速逼近和全局最优等特点， 同时将神经网络与分解预测相结合可以有效提高预测精度。

有鉴于此， 本文提出了一种基于风速分频特征和权值匹配的RBF 超短期风电功率预测方法。通过EMD 算法和层次聚类对风速序列进行分解和模态合并，从而得到不同频率的风速分量，之后根据不同频率的风速分量对于功率的影响大小，采用Yalmip-Cplex 优化算法对功率的权值进行优化。 仿真结果表明，与传统方法，如持续法和极限学习机模型ELM 相比， 本文方法的准确率更高，并且对于各种风速状况均具有较好的预测效果。

1 基于EMD 和层次聚类的风速分频特征提取

1.1 EMD 分解

经验模态分解是依据数据自身的时间尺度特征来进行信号分解， 基于其不需要提前设定任何基函数的特性， 使得EMD 方法可以实现对任何类型信号的分解。 非常适合处理非平稳及非线性数据，并且EMD 方法有很好的完备性和正交性，在其分解过程中会保留数据本身的特性[6]。

信号s（t）经过EMD 分解后，可用本征模态函数Cj（t）和残余分量rn（t）表示。

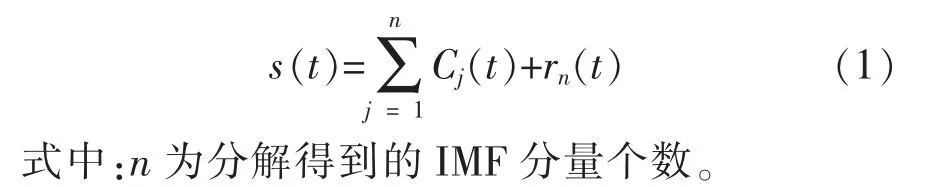
1.2 基于EMD 和层次聚类的风速分频特征提取

虽然经验模态分解过程中不需要提前设定基函数，克服了分析人员主观经验的干扰，但也因此无法控制本征模函数的个数， 同时会出现模态混淆的现象。层次聚类是一种常用的聚类算法，通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树[7]。 在聚类中一般通过数据之间的欧氏距离D 来对相似度进行刻画，两种不同类别数据之间的D 为

式中：xi，yi为两类模态变量第i 时刻的元素；N 为元素总数量。

本文采用的是自下而上的合并法， 通过计算各本征模函数之间的D， 进而根据不同模态变量之间的相似度进行层次聚类， 将相似度较高的模态变量合并为一类，最终得到NWP 风速高频、中频和低频分量。 层次聚类树形图如图1 所示。

2 基于风速分频和权值匹配的RBF 超短期风电功率预测方法

2.1 RBF 神经网络的输入输出

RBF 神经网络即径向基神经网络是一种新型高效的前馈式神经网络。 相比其他前向网络，RBF 具有结构简单、训练简洁、最佳逼近和全局最优等特点，因此被广泛应用于非线性优化、时间序列预测和模式识别等科学领域[8]，[9]。径向基采用高斯函数，RBF 的数学模型为

式中：x 为n 维输入向量；ci为第i 个基函数的中心；ci与x 均为拥有一样维数的向量；σi为基函数包围中心点的距离；n 为隐含层的节点数。

将经过EMD 分解得到的风速高频分量与对应时刻未分解的功率作为输入层的输入进行网络的训练， 进而通过最后一个月的风速高频分量对功率进行预测。同理，可以分别预测得到风速中频分量和低频分量对应的功率值。 RBF 网络功率预测模型如图2 所示。

图2 RBF 网络功率预测模型Fig.2 RBF neural network power prediction model

2.2 基于Yalmip-Cplex 的最优权值决策

WebSphere ILOG CPLEX 优化程序能够解决许多实际的大型优化问题， 同时具有其他优化程序所达不到的速度。 WebSphere ILOG CPLEX 能够以最快的速度最可靠地解决困难的数学优化问题，为解决线性规划、非线性规划和混合整型规划问题提供了很大的便利[10]。

对预测时刻前一个月不同风速分量预测得到的功率值进行加权相加，得到预测值，以准确率最高为目标函数通过Matlab 中的Yalmip-Cplex 优化程序对权值进行优化。

式中：PM为加权相加后所得到的预测功率；λi为通过不同风速预测得到的功率所对应的权值；i=1，2，3，分别为高频分量、中频分量、低频分量；Pi为通过不同风速预测得到的功率；PP为实测功率；R 为预测的准确率；Cap 为风电场开机容量。

由此可以得到一个月各个时刻的对于风速高频、中频和低频分量所对应功率的最优权值。

由于忽略风电机组损耗，根据风力发电原理，风电场输出功率为

式 中：Cpi，Pi，Vi分 别 为 第i 台 风 电 机 组 的 风 能 利用系数、输出功率和机组轮毅高度处风速；ρ 为空气密度；A 为风电机组叶轮扫风面积；ΔV 为风速高频分量扰动。

由式（7），（8）可知，高频分量在不同的风速段对于功率的影响是不同的： 对于幅值大小相同的风速，在低风速VL下，高频分量扰动ΔV 对于功率的影响相对较小；在高风速VH下，高频分量扰动ΔV 对于功率的影响相对较大。因此，根据不同风速频率分量进行预测，当处于低风速段时：风速高频分量对于最终预测值的贡献率应该较低；风速低频分量对于最终预测值的贡献率应该较高。

2.3 基于风速分频特征和最优权值匹配的RBF 超短期功率预测模型

基于经验模态分解方法在处理非平稳序列信号的特殊性以及Yalmip-Cplex 优化算法对RBF预测功率的权值决策的优越性， 本文提出一种基于风速分频和权值匹配的RBF 超短期风电功率预测模型，其流程如图3 所示。

图3 算法流程图Fig.3 Algorithm flow chart

基于风速分频和权值匹配的RBF 超短期风电功率预测流程描述如下。

（1）利用EMD 分解，将原始NWP100 m 风速序列分解成一系列相对平稳的IMF 分量和残余分量序列， 之后通过层次聚类对各分量进行模态合并，得到高、中、低频分量。

（2）分别对各频率分量建立RBF 预测模型，选取合适的扩散因子和神经元数量。最后，通过预测得到各分量序列的预测值。

（3）对于历史的各频率的功率预测值，以准确率最高为目标函数，通过Yalmip-Cplex 优化算法对各分量的求和权值进行优化。 再求取不同风速状况下各频率功率预测值的均值。

（4）将通过RBF 模型预测得到的各分量序列预测值根据预测时刻MWP 风速大小进行最优权值选择，加权求和即可得到功率预测值。

（5）将本方法的预测结果和其他模型的预测结果进行对比， 通过误差指标分析验证所提方法的精确性。

3 评价指标

按照 《QGDW10588—2015 风电功率预测功能规范》要求，超短期预测第4 个小时预测的月准确率应大于85%， 超短期预测月合格率应大于85%，限电时段的实际功率以理论功率替代。

设PMk为k 时刻的实际功率，PPk为k时刻的预测功率，N 为预测点的个数，则第4 小时预测的均方根误差r1为

按2.3 节步骤（1）～（5）输入仿真输入量，将模型计算的预测功率同实测功率经过3 种的误差评价标准式（9），（10），（11）进行误差计算，求得第4小时的r1，r2，r3。

4 算例分析

本文以黑龙江某风电场的实测数据以及NWP 数据为基础进行超短期预测并进行分析，采样间隔为15 min， 电场的总装机容量为70 MW。预测结果评价指标选用第4 小时的r1，r2，r3。

4.1 不同频率风速特征的提取

对于该风电场2016 年1 月1 日-4 月3 日共9 000 个点的NWP100 风速数据进行EMD 分解和层次聚类（图1）。 为了得到高、中、低3 种频率的风速分量，本文以欧式距离大小作为标准，将有限个本征模态分量聚为三类， 聚类效果如图4 所示。 由图4 可知，经过EMD 分解和层次聚类后，可以很明显地将原始NWP 风速序列分为频率不同的3 组分量， 为后续的分频预测提供了输入基础。

图4 不同频段的风速时间序列Fig.4 Time series of wind speed with different frequency

4.2 各风速段不同频率分量的最优权值分配

图5 为不同NWP 风速下各频率分量最优权值分布图。

由图5 可知，随着风速的增加，通过高、中频分量预测所得的功率所对应的低权值的分布逐渐减少，高权值的分布逐渐升高。 从而说明，随着风速的增加， 风速高频分量对于功率预测值的影响逐渐增大。

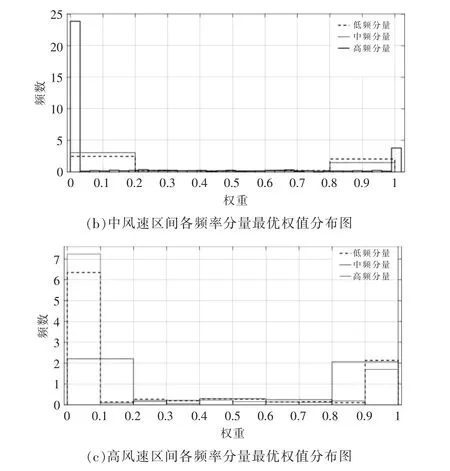
图5 不同NWP 风速下各频率分量最优权值分布图Fig.5 Optimal weight distribution of frequency components under different wind speeds

对风速数据区间进行3 等分， 将风速为1.24～4.42 m/s 定义为低风速区间，4.42～7.60 m/s定义为中风速区间，7.60～10.50 m/s 定义为高风速区间。 通过对不同风速段各频率分量的权值求取平均值（表1），可以看出低频分量所对应权值随着风速的增加而变大。证明了随着风速的增加，风速高频分量对于功率预测值的影响逐渐增大，风速低频分量对于功率预测值的影响逐渐减小。

表1 不同风况下的最优权值均值Table 1 The mean value of optimal weight under different wind speed

4.3 预测效果对比图

图6 为不同风速下各种方法预测效果对比图。 通过对比图6 中各种模型在不同风速下所示的预测值和实际值曲线可以得知， 各模型均表现出较为良好的预测效果。在不同风速下，由于对不同频率分量所设置的权值不同， 所以使得本文方法对于各种风速段的预测值均对实测值有很好的跟随效果。

图6 不同风速下各种方法预测效果对比图Fig.6 Comparison of prediction results of various methods under different wind speeds

为了更加直观地比较不同方法的预测效果，分别对本文方法、持续法和极限学习机ELM 模型的预测评价指标进行统计，结果如表2 所示。

表2 不同风速下各种方法预测结果评价表Table 2 Evaluation table of prediction results of various methods under different wind speeds

由表2 可知：本文方法在不同风速段的r1均小于10%，在低风速段和中风速段时，均高于持续法和ELM；在高风速段时，由于中频分量的权重所占比例最大， 而此时风速的波动情况较为剧烈， 因此使得预测功率不能很好地跟随功率实测值，造成预测误差偏大。

5 结论

本文采用EMD 分解将风速分解为不同频率的分量，通过输入RBF 神经网络得到不同频率的功率预测值，通过Yalmip-Cplex 优化算法对不同频率的功率分量进行权重参数优化。 通过对黑龙江某风电场进行实际算例分析，得到以下结论。

①通过对风速序列进行EMD 分解， 根据各模态分量间的欧氏距离进行层次聚类能够有效地将不同频率特征的风速提取出来。

②通过将历史不同频率的风速作为神经网络的输入，输出不同频率分量所对应的预测功率，以准确率最高为目标函数进行功率权值优化。 通过对权值分布的分析可知，随着风速的增加，风速高频分量对于功率预测值的影响逐渐增大。

③与传统的统计模型和RBF 神经网络相比，本文提出的基于风速分频特征和权值匹配的RBF 神经网络超短期功率预测模型能够有效地提高预测精度， 在各种风速状况下均表现出良好的预测效果。