基于K-SVD 字典学习的岩心图像压缩感知重构

唐新闰, 刘彦彤, 张 岩, 赵玉莹, 关正昊

(1.东北石油大学 计算机与信息技术学院, 黑龙江 大庆163318; 2.大庆油田勘探开发研究院 信息研究室, 黑龙江 大庆163000)

0 引 言

岩心是油气田勘探开发中重要的基础地质资料, 对其观察描述在确定岩性、 生储盖组合研究以及推断沉积环境中具有重要作用。 随着岩心图像采集设备的广泛使用, 岩心样本被扫描成数字形式存储, 在提升油气田勘探开发水平方面起到重要作用, 是实现油田数字化建设必不可少的内容。 由于多年的累积和不断新取心, 导致岩心数据量极其巨大。 因此, 研究适合岩心图像特点的压缩算法是非常有意义的[1]。 通过对大量典型岩心图像分析发现, 特殊的地质环境和复杂的地质变迁导致岩心图像普遍具有纹理信息丰富、 对比度较弱的特点, 传统压缩方法受Nyquist 采样定理的限制, 在低码率下影响边缘、 轮廓等高维奇异区域的保持效果[2-3]。 Donoho[4]和Candès[5]提出了压缩感知( CS: Compressed Sensing)理论与稀疏表示方法结合, 同时进行压缩与采样操作, 在信号具有可压缩性或稀疏性先验的条件下, 通过采集少量信号的投影值, 在接收端通过稀疏性约束方法就可以获得信号准确的重构, 在某种意义上突破了Nyquist 采样定理的瓶颈, 该方法对研究岩心等纹理信息丰富的图像压缩与处理具有重要意义[6-7]。

在实际应用领域直接采用CS 方法重构整幅图像将导致巨大的计算量。 分块压缩感知( BCS:Block Compressed Sensing) 方法在2007 年由Gan[8]提出, 该方法降低了存储和计算成本。 基于此,Mun 等[9]提出了BCS-SPL(Smooth Projected Landweber)算法, 将图像分块进行观测采样, 通过维纳滤波结合Landweber 迭代实现重构, 使用离散余弦变换、 离散小波变换等正交基作为稀疏基, 改善了BCS的重构效果, 但由于对各个图像块采用相同的采样率, 造成资源分配不合理, 且重构过程中存在一定块效应。 Fowler 等[10]提出多尺度分块变采样率压缩感知算法(MS-BCS-SPL), 对每一层小波分解设定不同的采样率, 改善了较低码率情况下的块效应现象。 但由于不同子块中的边缘、 纹理信息可能不同, 对每一层子块采用相同的采样率并不合理。 因此国内外专家与学者针对该问题进行了研究。李玉等[11]和 高东红[12]分别提出了根据图像边缘结构和纹理信息自适应分配采样率的方法, 在一定程度上减少了采样数量, 提高了重建性能。 但其只对小波分解后的低频系数进行重建, 而对于细节较复杂的图像重建效果不理想。 张学全等[13]根据图像块的内部活动性将图像块分为纹理块和平坦块, 通过邻块边缘自适应加权滤波方法消除了图像重构的块效应, 提高了图像边缘的保持, 但是对平坦块的检测比较耗时导致算法处理速度较慢。 此外当前图像压缩感知重构采用的稀疏表示基函数通常有Fourier[14]、 Wavelet[15]等正交变换。 Fourier 是一种全局变换, 不具有局部化分析的能力, 容易产生吉布斯现象; Wavelet 是一种时频局域性变换, 但在表示二维奇异线条情况下, 存在不光滑和模糊现象。基于K-SVD(K-Singular Value Decomposition)超完备字典学习的图像稀疏表示方法由Bryt 等[16]提出,学习型超完备字典能根据图像本身的特点, 自适应的调整变换基函数, 该方法在图像处理领域得到了广泛应用。

受上述研究的启发, 针对传统方法进行岩心图像压缩感知重构时, 在低码率下容易产生细节丢失的问题, 笔者提出了基于K-SVD 的重构算法, 并在BCS 算法的基础上, 采用高斯随机矩阵观测相应层级的图像块, 用MMSE 估计近似解获得初始解, 采用K-SVD 超完备学习字典稀疏表示岩心图像, 结合Landweber 迭代与自适应阈值方法实现岩心图像的压缩和重构。 通过仿真实验结果证明, 笔者方法重构的岩心图像能更好的保留岩心图像的纹理细节, 提高了图像的整体质量。

1 分块压缩感知重建算法

根据压缩感知理论, 假设x∈RN是长度为N 的原始信号, y∈RM是长度为M 的采样信号, 且M≪N,则观测值y 可用

表示。 其中Φ 是一个具有采样率为r=M/ N 的M×N 维的观测矩阵。

由分块压缩感知方法, 假设一幅大小为N×N 的图像x 被分成大小为B×B 的图像块, 第i 个岩心图像块向量化后表示记为xi, 在观测矩阵ΦB下得到的观测值

其中i=1,…,n, n =N/ B, B 的尺寸根据岩心图像重构的效率决定: 当B 较小时, 内存占用相对少且计算速度快; 当B 较大时, 图像重构的质量相对高。 ΦB是大小为MB×B 的正交观测矩阵, MB=(M×B) / N, M为整幅图像的观测采样值数目。 整个图像的观测矩阵Φ 为对角矩阵, 如下所示。

分块后观测矩阵ΦB的维数会相对降低, 显然式(1)是欠定的方程组, 无法根据y 求解x, 当具备图像数据x 在某个变换域C 下系数α 是稀疏的先验, 可以通过求解L1范数优化问题

2018年9月17日，美国森图斯能源公司(Centrus Energy)和韩国斗山重工建设有限公司(Doosan Heavy Industries and Construction)宣布双方已签署一份谅解备忘录，未来将在先进反应堆领域开展合作。

求解式(1)。 转化为求解凸优化的问题, 由于α 是具有稀疏性的先验, 可以利用不断促进α 稀疏性的方法求解, 即有

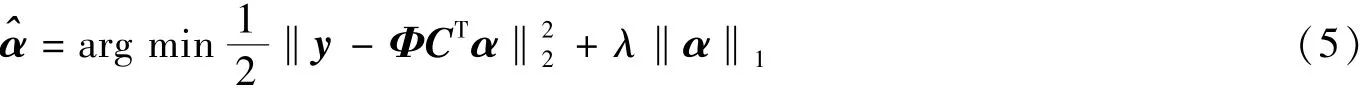
其中λ 是平衡因子, α 是α 的估计。 在促进α 稀疏性的过程可采用Landweber 冷却阈值迭代法, 其过程如下

标准Landweber 算法迭代重构图像亮度值可能是负数, 在选择松驰参数及控制收敛速度方面难度较大, Piana 等[17]为此提出改进的Landweber 算法, 在重构过程中利用先验, 得到投影Landweber 的方法,然后在传统Landweber 迭代过程中利用维纳滤波较弱块效应现象, 该方法不仅考虑信号的稀疏性还具有平滑的作用, 即在空间域内进行维纳滤波操作, 在变换域内实现平滑和阈值控制。

2 基于K-SVD 的压缩感知重构算法

2.1 自适应阈值算法

在分块压缩感知重构的基础上, 对岩心图像压缩感知重构操作中的实验参数进行研究, 发现Canny算法[18]等方法的阈值参数通常依据数据的先验知识或经验设定, 不能得到自适应图像特点的最佳阈值。全局和局部适应阈值法是目前广泛使用的计算阈值方法, 其中全局阈值时间复杂度较低, 与信号尺寸对数的平方根成正比。 岩心图像分块压缩感知初始解图像块的尺寸相对较小, 克服了因尺寸较大出现的“过扼杀” 系数后果, 所以选择计算岩心图像BCS 初始解图像块全局阈值, 实现根据岩心图像的自身特征计算阈值的重构操作[19], 计算公式如下

其中¯σ 是初始解中不同岩心图像块小波系数标准差的数学期望, M,N 为初始解的分解尺度。

依据式(7)得到阈值T, 另外需要具有筛选作用的阈值控制函数, 阈值控制函数中硬阈值函数与软阈值函数较为常见。 设信号数据可以由ω 表示, 阈值用T 表示, 符号函数表示为sgn(*), 软阈值函数为

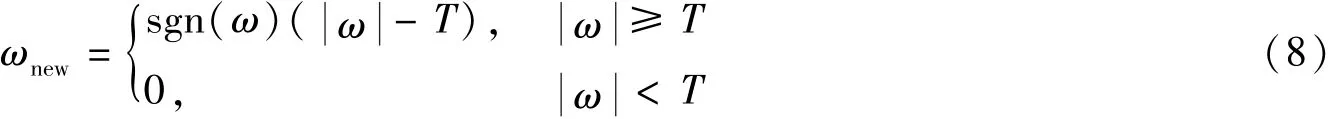
由式(8)可见, 软阈值函数首先比较ω 和T, 然后根据比较的结果再向0 进行收缩, 相比之下更符合极小与极大准则的理想值, 因此可以结合T 与软阈值控制函数实现筛选功能。

2.2 K-SVD 字典学习算法

目前在数字图像超完备字典学习方法中, K-SVD 表现出较高的稀疏表示效果[20], 在实际应用中具有高效、 灵活的特点, 因此笔者采用K-SVD 自适应学习获得岩心图像的稀疏表示基。

K-SVD 主要分两步操作: 第1 步为稀疏编码; 第2 步为字典更新。 令分别代表信号、 字典和稀疏表示向量,是N个信号集合,是S解向量集合, K-SVD 算法的目标方程如下

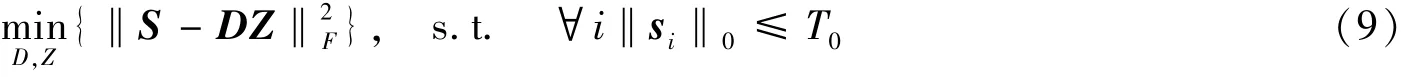
通过K-SVD 训练超完备字典的步骤如下。

1) 设定D0为超完备字典初始值: 超完备字典D0∈RN×M中的原子可以通过从信号样本x中任选的k个, 令k=0, 即D0为0 矩阵。

2) 稀疏编码阶段: 利用OMP(Orthogonal Matching Pursuit)算法[21]通过解t.‖y‖0≤k0, 以获得稀疏表达^yi(1≤i≤M), 并构成稀疏表达集y={y1,y2,…,yM}。

3) K-SVD 字典学习步骤: 令j0=1,2,…,m表示将要更新的原子dj0, 开始j0= 1, 从y中找出所使用原子dj0的列, 即在j0行中非零稀疏系数所在的位置

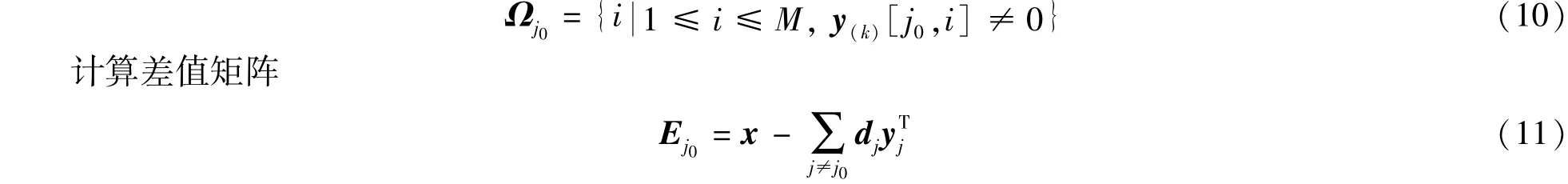
其中为y(k)矩阵的第j行, 依据Ωj0从Ej0中选择对应的列得, 通过SVD 算法得=UΔVT。 更新字典中的原子dj0=ui与对应的稀疏表示yR j0=Δ[1,1]·vi。

4) 当‖x-D(k)y2(k)F‖22≤ε时, 停止更新。

对岩心图像, 利用标准差σ¯ 和初始解尺度获得自适应阈值, 通过K-SVD 算法学习训练稀疏表示岩心图像的超完备字典, 得到岩心图像小波系数的标准差, 图1 给出了两幅岩心图像与稀疏字典图示。

图1 训练岩心图像与字典原子Fig.1 Training images and dictionaries

3 算法描述

首先基于分块压缩感知, 将岩心图像划分为尺寸相同的图像块, 通过高斯随机矩阵与每个图像块相作用, 获得对应的观测值。 接着利用MMSE 方法得到初始解的估计值, 然后采用提升小波基对初始解进行分解, 依据式(7)得到自适应阈值。 最后利用K-SVD 字典学习方法自适应阈值以及维纳滤波, 迭代求解, 实现岩心图像压缩编码和重构。 整体算法的具体步骤如下:

1) 读取原始岩心图像, 设定图像分块大小和采样率r等参数, 生成岩心图像子块与高斯随机矩阵ΦB;

2) 用ΦB作用于每个岩心图像块xi, 进行观测, 得到相应的观测值yi;

3) 用MMSE 方法获得岩心图像初始解的估计, 此时k=0;

4) 在初始解的基础上使用3×3Winner 的滤波器进行k次平滑操作;

5) 对初始解使用提升小波基进行分解, 获得小波系数标准差σi, 依据式(7)得到自适应的阈值T;

6) 设定迭代次数k和超完备字典D原子的个数Dn;

7) 对每一岩心图像块xi, 使用迭代;

8) 采用K-SVD 算法训练yi, 获得大小B2×Dn的超完备字典D;

9) 依据软阈值函数与T、 字典D重构岩心图像子块~xi;

11) 通过Oi+1=‖xi+1-x^i‖2计算残差, 其中i=i+1;

12) 当Oi-Oi-1＜10-2时, 得到重构的最优解, 迭代终止, 否则重新返回步骤7)。

4 实验结果及分析

实验环境采用Windows7 操作系统, 软件平台为Matlab R2013b 环境, 实现岩心图像的压缩与重构,并与BCS-SPL-DWT 和BCS-SPL-DDWT 算法的实验结果进行对比。 测试岩心采用尺寸为512×512 像素的图像, 通过高斯随机矩阵构造采样观测矩阵, 整体岩心图像划分成尺寸为B×B的子块, 超完备余字典D的原子个数为Dn(实验中取B=8,Dn=4), 则得到大小为B2×Dn的超完备字典D, 分别用离散小波变换(DWT: Discrete Wavelet Transformation)、 双树复小波变换(DDWT: Dual-plex Wavelet Transform)和K-SVD字典作为稀疏表示基, DWT 和DDWT 分别采用3 级分解。 表1 给出2 幅岩心图像在3 种不同方案下压缩与重构PSNR 值。 可见与其他两种方案实现岩心图像的压缩与重构的PSNR 值相比, 笔者算法的PSNR提高0.1 ～0.8 dB。

表1 3 种不同方案对岩心图像压缩与重构的峰值信噪比PSNR Tab.1 PSNR of the core image of compression and reconstruction with three schemes (dB)

图2 给出了采样率r=0.25 时3 种方法的结果。 由图2 可见, BCS-SPL-KSVD 重构的岩心图像质量相较BCS-SPL-DWT 约提高0.3 ～0.6 dB, 与BCS-SPL-DDWT 相比约提高0.1 ～0.4 dB。

图2 岩心1 的3 种方法对比(r=0.25)Fig.2 Comparison of three reconstruction methods for core image one

图3 岩心2 的3 种方法对比(r=0.25)Fig.3 Comparison of three methods for reconstructing core image two

5 结 语

笔者在分块压缩感知重构的框架下, 根据岩心图像的特点, 以全局阈值作为自适应阈值的依据,结合K-SVD 字典学习方法, 实现岩心图像的随机压缩采样观测与重构。 仿真实验证明, 笔者算法得到的岩心图像视觉效果和峰值信噪比均有所提升, 与BCS-SPL-DWT 和BCS-SPL-DDWT 算法相比, PSNR 值分别平均提高0.6 dB 和0.4 dB, 并且有效保留了岩心图像的纹理特征, 实现了对岩心图像较高质量的重构。