基于非线性声学共振法的CFRP板冲击疲劳损伤检测研究

朱利勇,尹嘉雯,韩 梦,魏 勤

(江苏科技大学 理学院, 镇江 212100)

碳纤维增强(carbon fiber reinforced polymer, CFRP)复合材料由于其质量轻、强度高以及耐腐蚀等优点,在工业工程中得到了广泛应用[1]．然而,由于制造不完善、意外冲击以及疲劳载荷,复合材料很有可能会产生损伤．这些损伤会严重地降低材料强度,最终导致材料结构失效[2]．因此,针对复合材料损伤检测技术的相关研究显得尤为重要．

传统的线性声学检测技术利用声波在介质内传播过程中的反射、透射以及能量衰减等特性进行损伤检测和定量分析．这种检测方法对声阻抗差别较大，对毫米级以上的缺陷具有较高的灵敏度,而对于微米级微观损伤的检出率并不是很高．相比之下,非线性声学检测技术对微米级损伤有着良好的检出率,并且对适度的环境变化以及形状复杂的检测结构具备一定的适用性,为主动结构健康监测的发展奠定了重要基础[3]．根据检测原理,非线性声学检测技术又可以分为高次谐波法[4]、混频法[5]、声学共振法[6]以及振动声调制法[7]．文中所涉及的是非线性声学共振法的检测研究．

通常,材料的非线性分为经典非线性以及非经典非线性两类．经典非线性主要与所施加应变的不同而引起的波速变化有关,其中最典型的现象就是响应频谱中产生高次谐波;而非经典非线性则是由于材料的耗散行为所导致的,其中典型的现象就是相应频谱中出现额外的频率分量以及共振频率的偏移等．非线性声学共振法属于非经典非线性的范畴,随着材料中的损伤日益累积,材料的刚度逐渐降低,使得弹性波发生畸变,在激励能量递增的情况下,导致共振频率产生左偏现象．由于非线性声学共振检测方法对金属以及复合材料中的微观损伤都具有较高的敏感性,因此得到了研究人员的广泛关注．文献[8]利用非线性声学共振技术检测了两个处于机械循环载荷下的牛骨．结果表明,通过相应的非线性参数可以实现牛骨渐进疲劳损伤的定量评估．文献[9]采用非线性声学共振法和非线性振动声调制法对复合材料的低速冲击损伤进行了检测评估．文献[10]使用非线性声学共振检测技术分别针对钢-TiC复合梁、玻璃棒和聚合物基梁3种不同材料中的渐进损伤进行了相关检测．文献[11]采用非线性声学共振方法研究了不同纤维的层压顺序和织物类型对碳纤维复合材料非线性响应的相关影响．文献[12]使用非线性声学共振技术检测了一定应力和腐蚀条件下的钢棒试样．结果表明,随着损伤的积累,测试试样的共振频率明显向左偏移,且损伤程度越大,偏移率越大．国内有关非线性声学共振法的研究相对较少,文献[13]采用非线性声学共振检测技术来表征金属结构表面的非均匀沉积状态．文献[14]开展了非线性共振检测研究,用来评估冻融循环中混凝土样品的渐进损伤．文献[15]利用单次冲击和多次冲击的非线性共振检测技术监测混凝土中的渐进碱-硅反应．

文中通过摆球冲击实验向CFRP复合材料板引入渐进冲击疲劳损伤,对完好以及不同损伤程度的试样进行非线性声学共振检测,并通过相应的非线性参数定量表征试样的损伤程度;建立基于CFRP复合材料刚度退化的疲劳损伤模型,对其剩余疲劳寿命进行评估和预测．

1 基本理论

1.1 非均质材料的滞后非线性

近年来,已有大量的相关研究表明,岩石、混凝土以及复合材料等非均质材料在受损后具有复杂的柔顺性,表现出非线性行为,并且无法用经典的非线性理论来解释,而相应的应力-应变曲线可能表现出典型的非线性、滞后和离散记忆[16]．根据胡克定律,最广泛使用的一维应力-应变关系可以表述为:

(1)

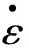
(2)

一般来讲,当非均质材料中所施加的应变幅值>10-6时,非线性滞后参数αf占据主导地位,并且可以表述成[8-15]:

(3)

式中：f为应变ε处的共振频率；f0为初始应变ε0处的共振频率，即完好试样的共振频率．

为了得出式(3)的对应应变ε,引用Van Den Abeele的自由边界梁应变-速度表达式[18]:

(4)

式中：T为试样的厚度；L为试样的长度；f为共振频率；v为一段时间内通过积分加速度数据确定的速度．

1.2 冲击疲劳损伤模型

疲劳损伤演化机理是研究疲劳行为的重要关注点之一,也是预测材料剩余疲劳寿命的基础．众所周知,复合材料的疲劳损伤和失效机理要比金属材料复杂得多．一般来讲,在多次冲击载荷作用下,冲击疲劳损伤逐渐累积,从而导致复合材料的机械性能发生变化,例如材料强度或者刚度的退化．而复合材料有4种基本失效类型,分别为基体开裂、脱粘、分层以及纤维断裂[19]．近十几年来,为研究复合材料疲劳损伤的演化发展进程并预测其剩余疲劳寿命,相关研究人员对此做出了大量的疲劳试验,并提出了相应的模型．在损伤力学中,疲劳损伤变量D通常被用来描述材料中疲劳损伤的连续发展进程,可表述为[20]:

(5)

式中：D0为初始疲劳损伤变量；N为冲击疲劳次数；Nf为试样失效时对应的冲击疲劳总次数；N与Nf的比值为冲击疲劳寿命；D0和b均为待定系数．

2 试样准备及实验系统

2.1 冲击疲劳损伤试样

实验选用由环氧树脂胶结而成的多层碳纤维增强复合材料板,其铺层方向为[04/904]S,试样尺寸为250 mm×25 mm×4 mm．图1为摆球冲击装置的左视图以及夹具图像,通过改变摆球的质量m,摆长l以及摆角θ,可以向复合材料试样引入不同冲击能量的低速冲击疲劳损伤,各试样对应的冲击能量参数见表1．

图1 摆球冲击装置Fig.1 Sketch of pendulum impact device

表1 冲击能量对应参数Table 1 Corresponding parameters of impact energy

2.2 非线性声学共振实验系统

非线性声学共振实验装置系统,如图2．首先,由函数信号发生器(Tektronix AFG 3102C)产生一个正弦信号波,并经过宽频带电压放大器(Falco WMA-300)放大,以驱动一个电阻4 Ω、功率3 W的扬声器,该扬声器用石蜡粘合于复合材料试样的表面中心位置,用以激励试样产生振动．一个质量约为1.6 g的微型加速度传感器用石蜡粘合在试样的右端,用来获取试样的振动响应,该响应信号通过电荷放大器(YE5856)放大,并由动态数据采集器(东华5922D)采集,采样频率设置为10 kHz．整个复合材料板试样被放置在一块柔软的海绵上,用来模拟自由边界条件．最后,在计算机上对采集的信号进行快速傅立叶变换信号处理．

图2 非线性声学共振实验装置Fig.2 Experimental setup of nonlinear acoustic resonance

在进行非线性声学共振实验之前,需要确定完好试样的共振频率f0,同样使用这套实验装置系统,取一块完好试样进行宽频带扫描(100 Hz～10 kHz),设置扫频幅值为5 Vpp,持续时间为21 s,此时动态采集器的采样频率设置为20 kHz．扫频结束后,对所采集的扫频信号进行快速傅立叶变换得到对应的频率谱,为了达到约10-6的振动应变,应选择具有较大振幅的振动模态作为共振频率．

在确定共振频率后,重新设置扫频范围为共振频率左右各50 Hz(扫描长度为100 Hz),进行非线性声学共振实验,激励电压以每2.5 V从52.5 V逐渐增加到65.0 V对试样进行重复测试．测试结束后,将试样放置在加热平台上加热,以移除扬声器和加速度传感器,之后向试样引入冲击疲劳损伤,并循环测试,直至试样损坏．

3 结果与讨论

3.1 共振频率

未受冲击的完好试样共振频率频谱呈现出3种振动模态,分别为750、1 360、2 350 Hz,如图3，从图中可以看出,第2阶振动模态(1 360 Hz)的幅值最高．为了获得足够强的振动,选择1 360 Hz作为此次非线性声学共振实验的共振频率f0．

图3 完好试样的共振频率频谱Fig.3 Resonance frequency spectrum of intactspecimen

3.2 非线性声学共振测试

确定共振频率f0后,首先对完好试样进行非线性声学共振测试,其响应频谱如图4．从图中可以看出,随着激励电压的增加,幅值-频率曲线的幅值明显增加,而共振频率几乎保持不变．

图4 完好试样的非线性声学共振谱Fig.4 Nonlinear acoustic resonancespectrum of intact sample

之后,对4块同质试样分别进行3、4、5、7 J的摆球冲击实验,对于3、4、5 J的冲击能量,每冲击100次进行一次非线性声学共振测试,而对于7 J的冲击能量,每冲击5次测试一次．图5为各试样在不同冲击能量以及冲击次数下的非线性声学共振测试频谱图．实验结果表明,随着激励电压的增加,幅值-频率曲线的幅值同样明显增加,但与完好试样不同的是,损伤试样的共振频率逐渐减小．

图6为相对频率偏移(f-f0)/f0与激励电压U之间的关系,其中各点代表实验所测得的数据,而直线是对应的拟合直线．由于损伤试样的共振频率发生左偏,根据式(3),此时应变ε下的共振频率f要小于初始共振频率f0,因此相对频率偏移为负值,并且随着激励电压的增加表现出较好的线性关系．

图5 损伤试样的非线性声学共振谱Fig.5 Nonlinear acoustic resonance spectrumof damaged specimens

图6 相对频率偏移与激励电压之间的关系Fig.6 Relative frequency shift relationswith excitation voltage

3.3 冲击疲劳损伤评估

表2为各个试样失效时对应的冲击疲劳总次数Nf．

表2 各个试样的冲击疲劳总次数Table 2 Total number of impact fatiguetimes for each specimen

通过式(3、4),计算了各个损伤试样不同冲击疲劳次数N下的非线性参数|αf|,如图7．可以看出,随着冲击疲劳次数的增加,各个试样的非线性参数|αf|都表现出增长趋势,且变化趋势大致相似．数据的波动是由于扬声器和加速度传感器的粘合位置等因素导致的．

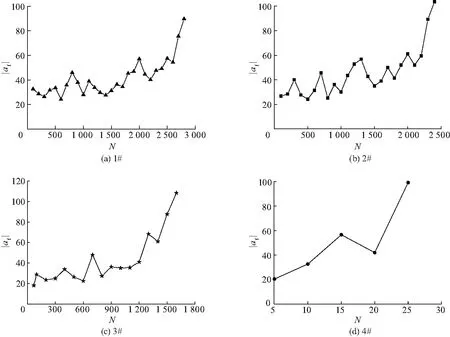
图7 非线性参数|αf|与冲击疲劳次数N之间的关系

图8为各个损伤试样非线性参数|αf|与冲击疲劳寿命N/Nf之间的关系,其中实线为拟合曲线．可以看出,在冲击疲劳寿命前40%时,非线性参数|αf|缓慢递增,并且大多都集中在20～40,这是由于冲击疲劳次数N相对较少,试样的损伤程度较小的原因;而当冲击疲劳寿命达到80%之后,|αf|呈现指数式递增,直至达最大值103.51,这是因为随着冲击疲劳次数增加,复合材料的强度或刚度逐渐退化,微尺度的冲击疲劳损伤持续累积并达到一定的程度,从而引起了质的变化,最终演变成肉眼可见的宏观损伤,导致材料失效,这与之前的非线性声学共振测试结果相一致．

图8 非线性参数|αf|与冲击疲劳寿命N/Nf之间的关系Fig.8 Relation between nonlinear parameter |αf|and impact fatigue life N/Nf

通过拟合,非线性参数|αf|可作为疲劳损伤变量D的函数,其表达式为:

(6)

将式(5)代入式(8),非线性参数|αf|又可以写成:

(7)

表3为各个试样在式(7)下所得出的拟合参数D0和b的值,可以看出,各个试样的拟合参数D0非常接近,这是由于复合材料在制备过程中,受到制备工艺以及外部环境等影响,难免会存在空隙等内部损伤,从而导致材料本身的非线性．而这4块试样是从同一材质的碳纤维复合材料板上所切割下来的,因此初始疲劳损伤变量D0大致相当．通过之前非线性声学共振测试结果与疲劳损伤模型拟合结果的比较,证明了该公式对复合材料剩余疲劳寿命的评估和预测具有一定的适用性．

表3 各试样的拟合参数Table 3 Fitting parameters for each specimen

4 结论

(1) 非线性声学共振检测技术能够很好地区分完好试样以及损伤试样,对于损伤试样,随着激励电压的增加,共振频率逐渐减小,并且相对频率偏移与激励电压有着良好的线性关系．

(2) 用于评估冲击疲劳损伤的非线性参数|αf|随着冲击疲劳次数N的增加而增大,且|αf|在冲击疲劳寿命初期缓慢增加,在达到冲击疲劳寿命的80%之后迅速递增．

(3) 所建立的复合材料冲击疲劳损伤评估和剩余疲劳寿命预测的模型与非线性声学共振方法的测试结果吻合较好．

然而,由于材料材质、非线性参数以及理论模型等因素影响,对复合材料剩余疲劳寿命预测的研究尤为困难,这需要大量的实验和数据加以验证．因此,在更多的非线性实验测试以及更详细的疲劳损伤模型方面值得进一步研究．