唐山市房价

贾健英

[提要] 近年来，唐山市房价总体呈上升趋势。为拟合唐山市房价非线性趋势，以2019.07～2020.06房价均价作为样本数据，建立GM（1，1）模型，然后基于静态和等维递补动态GM（1，1）预测模型对2020.01～2020.06房价进行检验性预测。结果表明：等维递补动态模型预测效果优于静态模型，相对误差率较低，能较好的对唐山市房价进行分析和预测。最后基于等维递补动态GM（1，1）模型对唐山市2020.07～2020.12房价进行预测，为政府部门决策提供参考依据。

关键词：唐山;GM（1，1）模型;等维递补;房价预测

中图分类号：F293.3 文献标识码：A

收录日期：2020年8月17日

中国指数研究院数据显示，唐山市目前房价均价高于8，000元/平方米，并且持续平稳上涨。唐山市作为河北省经济强市，房价迅速上涨给市民购房带来沉重压力。2020年4月，中央继续运用降准、降息等积极的货币政策加大金融支持力度，保持流动性合理充裕。为保证房地产市场平稳运行，保持房价稳定，需要坚持“房住不炒”的理念，实施老旧小区改造。国务院和发改委接连发文，在强调区域发展的同时，分别从土地、人口和资金等方面提出改革意见，进一步激发全社会创造力和市场活力。所以，对唐山房价进行分析与走势预测有重要意义。

一、灰色GM（1，1）模型简介

邓聚龙教授于1982年提出了灰色系统理论，在经济生活中，经常遇到了解部分信息却不能掌握全部信息的问题，而灰色模型可以较好地解决此类问题，能应用于社会科学与自然科学的许多领域。灰色预测需要对原始时间序列数据进行处理，使其成为有规律的序列后进行建模。该模型一般只需要4个样本数据就可依据灰色序列进行预测，操作简便，并且解决了由于数据量少、信息不确定而无法研究或难以研究的问题。因此，该模型在我国经济中得到非常广泛的应用。灰色模型基于常微分方程理论基础，用GM（M，N）表示，其中，M代表常微分方程的阶数，N代表变量的个数，阶数或变量个数过多都可能导致预测效果不佳。因此，在实际研究中GM（1，1）模型预测方法最为常见。

房地产价格受土地开发利用及地价、房地产开发投资、人口需求、居民收入水平等诸多供给和需求因素影响，他们共同决定房价的变动，如此多的影响因素只通过几个变量很难对房价解释清楚。表明房价系统具有明显的灰色性，灰色GM（1，1）模型不考虑一个系统究竟包含多少因素，只运用自身的时间序列进行建模，所以适合用GM（1，1）模型对唐山市房价数据进行分析。

（一）GM（1，1）建模步骤

1、判定是否可以用GM（1，1）建模。基于指数发展的灰色模型，原始序列需满足指数变化规律。所以在建立灰色GM（1，1）模型之前，需要判断原始序列是否适合用GM（1，1）建模。常用的判定方法为级比检验，即通过计算原始序列的级比来保证GM（1，1）建模的可行性。

假设原始时间序列为：

x（0）=（x（0）（1），x（0）（2），…，x（0）（n）） （1）

级比检验：序列x（0）之间的错位相除：

λ（k）=，k=2，3，4，… （2）

λ（k）称为“级比”，如果所有级比满足λ（k）∈（e，e）（k=2，3，4，…），则可用GM（1，1）建模。

2、数据累加。x（0）为原始时间序列，建立GM（1，1）模型前，为了减弱原始序列的随机性，使用AGO方法对x（0）进行累加，生成较为有规律的新序列x（1）：

x（1）=（x（1）（1），x（1）（2），…，x（1）（n））

=（x（0）（1），x（0）（1）+x（0）（2），x（0）（1）+x（0）（2）+x（0）（3），…） （3）

其中，x（1）（k）=x（0）（i），k=1，2，3，…，n

3、建立GM（1，1）灰色微分方程。为了求解常微分方程时，可以得到指数变化的常微分模型，建立单变量的一阶线性动态灰色微分方程：

x（0）（k）+az（1）（k）=b （4）

式中，z（1）（k）=1/2（x（1）（k）+x（1）（k-1））（k=2，3，4，…），x（1）（k）为紧邻均值生成的数列，生成z（1）（k）的目的是采用取均值的平滑方式降低原始数据奇异值对模型的影响程度。

（4）式中x（0）（k）和z（1）（k）为离散的序列，为了把（4）式转化成连续的微分方程，需要对其进行白化：

+ax（1）=b （5）

其中，a和b为待估参数，分别称为发展系数和灰作用量。

4、求解模型。将（4）式转化成矩阵的乘法形式：

Y=Bu （6）

其中，Y=（x（0）（2），x（0）（3），…，x（0）（n））T，u=（a，b）T，B=-z（1）（2） 1-z（1）（3） 1 …  …-z（1）（n） 1

利用最小二乘法求解（6）式，求得u的估计值=（，）T=（BTB）-1BTY

把求出来的a和b的值插入到（5）式中，利用一阶线性微分方程的求解方法，得到x（1）序列的预测值：

（1）（k+1）=x（0）（1）-e-ak+ （7）

由于建模之前对数据进行了累加，进一步对（7）式進行累减，得到原序列的预测值为：

（0）（k+1）=（1）（k+1）-（1）（k），k=1，2，3，…，n（8）

5、GM（1，1）模型检验。建立GM（1，1）模型之后，需要检验模型是否有较高的精度，达到预期标准即可应用于预测研究。一般有以下3种检验方法：

（1）相对残差Q检验。求出原始数据序列x（0）（k）与预测序列（0）（k）的残差序列ε（k）、相对残差△k和平均相对残差：

ε（k）=（0）（k）-x（0）（k），△k=×100%，Q=△k

平均相对残差Q越小，表明模型精度越高，一般要求Q<0.1。

（2）方差比C检验。原始序列x（0）（1）和残差ε（k）的均值分别为和，方差分别为S12和S22，求出方差比C：

S12=（x（0）（k）-）2，S22=（ε（k）-）2，C=

均方差比C越小，精度越高。

（3）小误差概率P检验。

p=P{ε（k）-<0.6745S1}

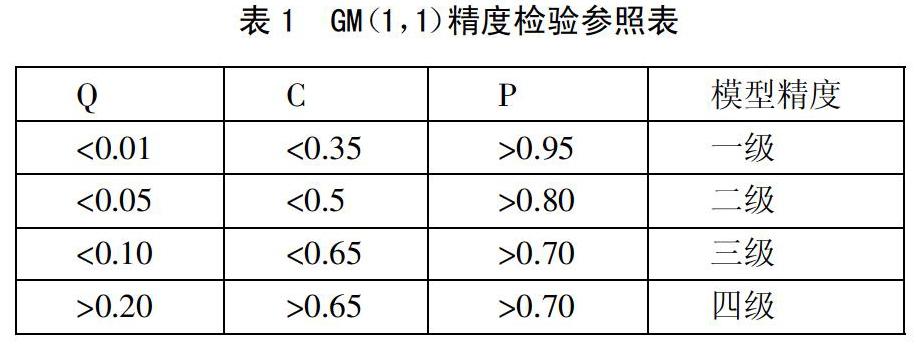
小概率事件一般不会发生，因此，p值越大，模型拟合精度越好。（表1）

（二）等维递补GM（1，1）预测模型。等维递补GM（1，1）预测模型，能够充分利用最新信息来降低灰度，及时地反映系统的变化，具有较高的预测精度。其预测步骤为：首先对原始序列x（0）=（x（0）（1），x（0）（2），…，x（0）（n））建立GM（1，1）模型，计算可得第一个预测值x（0）（n+1），为了保持维数不变，在序列最后加入x（0）（n+1），并去掉x（0）（1），组成新样本x（0）=（x（0）（2），x（0）（3），…，x（0）（n+1）），重新建立灰色模型，得到第二个预测值。如此类推，不断引入最新信息，去掉最老信息建立模型，预测下一个值，直到完成预测任务。

二、唐山市房价预測实证分析

（一）建立GM（1，1）模型。建立灰色模型需要“小样本”数据，所以选取2019.07～2019.12唐山市房价均价作为样本数据，数据来源于中国指数研究院。房价走势见表2。（表2）

对2019.07～2019.12数据建立GM（1，1）模型，由（1）式得原始数据序列：

x（0）=（7779，7974，8050，8072，8101，8162）

对原始数据进行级比检验，由（2）式求得：

λk=（0.9755，0.9906，0.9973，0.9964，0.9925）

n=6时，λk∈（e，e）=（0.7519，1.3307），满足级比检验条件。

然后对x（0）进行累加，生成新序列：

x（1）=（7779，15753，23803，31875，39976，48138）

根据最小二乘法计算可得灰色系数：

u=（a，b）T=（-0.0053，7924）T

把a和b的值插入到（7）式中，得到x（1）序列GM（1，1）预测模型：

（1）（k+1）=1502873e0.0053k-1495094 （9）

将k=1，2，…，5代入（9）式，得到累加序列拟合值，进行一次累减，计算得到原始序列拟合值，见表3。（表3）

由表3可见，唐山市房价的拟合值与实际值相差不大，表明利用GM（1，1）建模拟合效果较好。经检验，小误差概率P=1，方差比C=0.0939<0.35，平均相对误差率Q=0.0013<0.01，符合一级精度要求，且发展系数a∈（-2，2），可用于对唐山市房价进行预测。

（二）基于静态和等维递补动态模型的检验性预测。基于传统静态GM（1，1）模型直接对唐山市2020.01～2020.06月平均房价进行预测，为了对比预测效果，建立了等维递补动态GM（1，1）预测模型，两种模型预测结果见表4和表5。（表4、表5）

由表4和表5可见，两种模型的平均相对误差率较低，并且通过了方差比和相对误差检验，预测效果较好，但等维递补动态预测值更接近实际值，所以选择动态GM（1，1）模型进行唐山市房价预测研究。

（三）基于动态GM（1，1）模型的唐山市房价预测。根据等维递补动态模型对2020.07～2020.12唐山市房价进行预测，预测结果见表6。（表6）

三、结论

本文首先建立唐山市房价GM（1，1）模型，拟合值与预测值对比发现，该模型拟合效果较好并且符合精度要求。然后，对静态和等维递补动态GM（1，1）两种模型进行检验性预测，对比分析可知，等维递补动态模型在唐山市房价的预测效果上均优于静态模型。最后选择动态GM（1，1）模型对唐山市2020年7月～2020年12月平均房价进行了预测，结果表明，未来几个月唐山市房价整体呈小幅增长趋势。

主要参考文献：

[1]李广胜，郭欢.基于GM（1，1）模型的南京市房价预测研究[J].江汉大学学报（自然科学版），2020.48（02）.

[2]卓金武，魏永生，秦健，李必文.MATLAB在数学建模中的应用（第2版）[M].北京：北京航空航天大学出版社，2014.

[3]孟洁，张文博.基于GM（1，1）模型的北京市商品房房价预测[J].中国市场，2014（46）.

[4]汤文彬.我国房地产价格影响因素实证分析[J].价格理论与实践，2016（01）.

[5]门可佩，曾卫.中国未来50年人口发展预测研究[J].数量经济技术经济研究，2004（03）.