基于层析分析法的经济模型建立及分析

邵创新 张建霞 李锐欣 迟明路

摘要：本文以疫情下的整体经济为研究对象，首先选取自然、人口、科技、文化教育、农业、金融、政策干预、疫情态势和国际投资援助等因素作为影响经济发展方向的条件，建立相关的经济数学模型;然后运用层次分析法估算经济在不同条件下的相关权重;最后得出如下结论，疫情期间有利的政府干预和疫情态势将决定经济的走势，具体为两种情况即持续衰退和经济反弹，若相关政府政策不能及时落地，各项产业会受到不同程度影响，GDP也将持续降低;若疫情在未来时间得到有效控制，大部分各项经济产业可以复苏，经济将出现拐点，出现经济反弹。基于层析分析法的经济模型建立及分析较好展现出了疫情下的整体经济及未来发展趋势。

关键词：层次分析法;经济;数学模型;持续衰退;经济反弹

受新冠疫情在全球扩散的影响，在疫情出现之前，全球主要经济体半数以上已徘徊在衰退边缘，疫情的冲击很可能将它们迅速推入衰退之中[1]。即便处于低失业率与低通胀率的“梦幻组合”之中的某些国家经济[2]，疫情的冲击和资产价格的暴跌很可能快速打破其这些年在资产价格、财富效应、消费、就业之间所形成的良性循环，把经济拖入衰退之中，另外受新冠疫情在全球扩散的影响，世界经济也将受到相关影响[3-4]。为了对疫情下整体经济进行分析及预测，利用层次分析法对其进行建模和分析。

一、基于层次分析法的模型建立

首先确定评价指标，得评价要数集。评价要数集的设置对应的经济评价，其评价要素具体为B={自然因数、人口、科技、文化教育、农业、金融}。确定定性指标评语集合相應特征，对指标D可用如下评语集即D={比较差、一般、中等、良好、优秀}，那么隶属函数可以对定性指标变量进行评价，其区间可以表示为[0，1]，并在其区间中运用适当的模糊数来处理。本文采用线性隶属函数，其值分别为{0.2 0.4 0.6 0.8}。然后，对于相应的特征值进行一一求解。因为各个评价指标的量纲、类型及物理含义都是不太一样的，那么就不能够进行直接比较。所以，评价指标比较以前，对于其要进行处理和归一化，使得不同的指标可以进行直接比较与分析。

（一）最优指标特征值的确定

i、j的值分别为i方案j指标，假设最大指标特征值对应的隶属度是1，最小指标特征值对应的隶属度是0，可得相对优的对应隶属度如公式（1）所示。

那么，越小最优指标特征值通过上述公式（2）确定。

（二）评价因数指标权重向量的确定

此模型用层次分析法[5]进行评价，目标层A为经济趋向。措施层C1，C2，C3分别为政策干预、疫情态势和国际投资援助。准则层P1，P2，…，P9分别为自然因数、人口、科技、文化教育、农业和金融，对于这样设定的递阶层次结构，假设准测是上一层元素C，P1，P2，…，P9是它的下一层元素。P1，P2，…，P9需要进行一一确定，那么其对于准则C的重要性就是相对应的权重值，具体包括两种情况。

（1）如果P1，P2，…，P9的重要性可定量，其权重可直接确定。

（2）如果无法直接定量，需要进一步对问题的复杂性进行分析，那么通过比较对于权重值最终确定。

具体是指比较n个因素C1，C2，…，Cn对于其上面一层O的影响权重值，就是需要确定其在O中所占的一个权重比例值。对于其中的不同因素Ci与Cj，通过aij对影响权重值进行表示，利用1-9对aij（i，j=1，2，…，n）进行度量，它们代表的意义如表1所示。以aij（i，j=1，2，…，n）为元素构成的矩阵A=（aij）m×n称为判断矩阵。明显可以看出aij>0，且，根据此数学表达式可以得出矩阵A为正互反矩阵。

通过正互反矩阵的性质可以知道，只需对A的上（或下）三角的个元素进行求解就可以。

又已知矩阵A中的元素是可以传递的，满足（），则称A为一致矩阵，简称一致阵。具体含义如表1所示。

准则层对目标层的比较判断矩阵形式如表2所示。

对于准则C，n个元素之间相对重要性的比较得到一个两两比较判断矩阵。

其中Pij表示Pi和对的影响之比，P称为正互反矩阵。

相应的指标层对于其准则层的比较判断如表3所示。

（三）一致性校验

整个建模过程中通过1：9比例度量构造一致矩阵相对来说比较困难，大部分3阶及其3阶以上的比较矩阵并不是一致阵。

假设A是n阶正互反矩阵，λmax为A的最大特征根，则A的一致性指标如公式（3）所示。

二、基于层次分析法的模型求解

（一）层次结构图的建立

层次结构模型的建立运用层次分析法进行评价。目标层O为经济的发展方向。准则层C1，C2，C3，C4分别为自然因素、人口、科技、文化教育、农业、金融，子准则层P1，P2，P3分别为政策干预、疫情态势、国际投资与援助。其层次结构图如图1所示。

（二）矩阵表格的建立

构建准则层判断矩阵如表5所示。

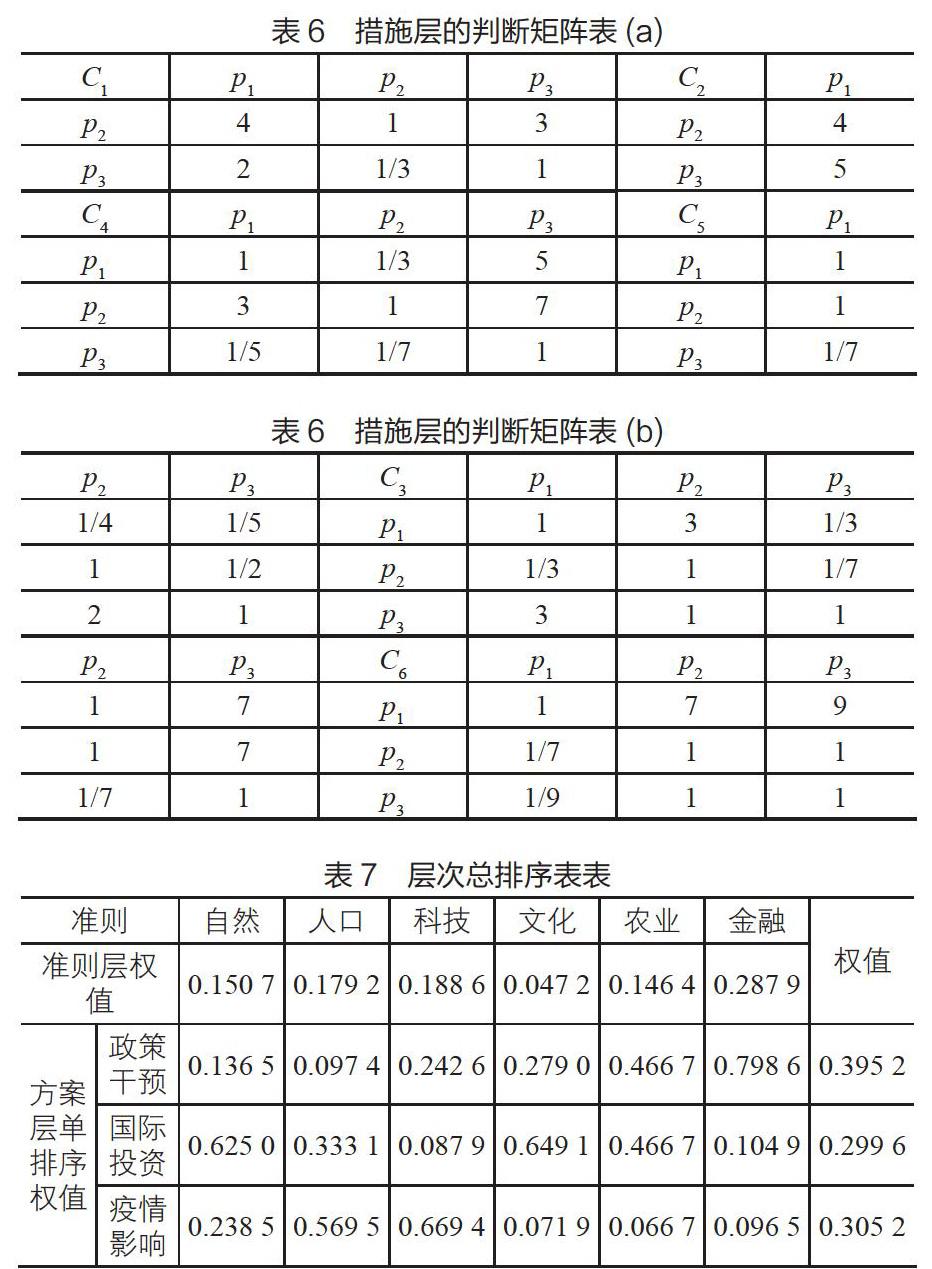
措施层的判断矩阵如表6（a）与（b）所示。

通过MATLAB程序的求解，可得到如表7所示的层次总排序结果。

三、结语

由于受到疫情影响，各个经济产业链受到明显影响，运用层次分析法估算经济在不同条件下的相关权重。疫情期间，相关有利政府干预，疫情态势将决定经济走势，具体分析包括两种情况，分别是持续衰退，若相关政府政策不能及时落地，各项产业会受到不同程度影响，GDP也将持续降低;经济反弹，通过层次分析可知疫情影响权重较大，若疫情在未来时间得到有效控制，大部分各项经济产业可以复苏，经济将出现拐点，有可能会出现经济反弹。

参考文献：

[1]宋国友.美国经济复苏面临五大矛盾[N].环球时报国际论坛，2020-7-28（015）.

[2]周长锋，孙苗.美国经济政策不确定性对中国金融市场波动的影响[J].福建金融，2020（7）：35-41.

[3]沈国兵.新冠肺炎疫情全球蔓延下美国国债的可持续性分析[J].广西财经学院学报，2020，8，33（4）：10-24.

[4]高炜宇.美国经济衰退的可能性及其对中国经济的影响分析[J].科技发展，2019，9（130）：51-57.

[5]王玉珍，李佳儒，李焱.基于层次分析法县域电商发展影响因素评价研究——以甘肃省为例[J].洛阳师范学院学报，2013，8，39（8）：60-64.

基金项目：2019年度河南省高等教育教学改革研究与实践项目（2019SJGLX485），河南工学院博士科研启动资金项目（KQ1812），教育部产学合作协同育人项目（201902155006）。

作者简介：邵创新（2000—），男，本科在读，学生，主要从事数学建模在各领域中的应用研究。