考虑策略顾客的双周期双渠道供应链定价决策
2020-11-16雷倩,何娟,马超
雷 倩,何 娟+,马 超
(1.西南交通大学 交通运输与物流学院,四川 成都 610031; 2.湖北文理学院 汽车与交通工程学院,湖北 襄阳 441053)
0 引言
近年来,众多制造商在将产品销售给传统零售商的同时,也通过网上直销渠道销售自己的产品,如苹果、耐克、惠普、保罗男装[1]。制造商开辟的网络直销渠道是零售渠道的有力竞争者,直接影响零售商的利益,必然会带来“渠道冲突”。2013年年初,以纯关掉了天猫旗舰店等电商平台的直销渠道,彻底退出了电商[2]。为了解决双渠道冲突问题,目前,大多企业采取线上线下产品区分的方案,其好处可让直销渠道和零售渠道形成两套不完全相同的产品体系,采用不同的销售策略,以协调网络直销渠道和传统零售渠道的关系。例如李宁,直销渠道销售的是过季产品和部分新品,而零售渠道则以新品为主[3]。按照产品销售时间顺序来看,制造商将整个销售过程分为两个周期(1)由于消费者需求不断升级,电子产品、时尚品这类季节性流行商品更新换代的进程加快,当距离产品生命周期结束较近时其产品价值往往较低,因此,本文主要研究产品的前两个销售周期。:在第一周期,在直销渠道和零售渠道同时销售新品;在第二个周期,只在直销渠道销售过剩产品。事实上,唯品会的成功也是得益于这个策略,其主营业务为在线销售品牌折扣商品,即不定期地对线上线下卖不完的库存做尾货特卖活动。此外,很多商家会在特定的节日进行第二周期的在线促销,如阿里巴巴“双十一”(2)在2018年“双十一”,网上最终交易额为2135亿元,比去年同期增长了27%,见https://wallstreetcn.com/articles/3435709?ivk=1。,京东“618”,美国的“Cyber Monday(网络星期一)”(3)根据美国数据分析商Adobe Analytics数据,2018年美国网络星期一销售额超过79亿美元,同比增长19.3%,破美国单日商品销售额纪录。详见http://www.zaobao.com/realtime/world/story20181128-911482。。
双渠道供应链和双周期供应链作为影响企业发展的两种销售模式,均是近年来供应链研究的热点问题。关于双渠道供应链管理,其研究重点包括定价问题。刘灿等[4]研究了展厅效应对双渠道最优定价、服务水平和价格竞争的影响;周健等[5]考虑了搭便车现象的双渠道定价策略;申成然等[6]考虑了部分消费者对比价格后优先在网络渠道购买产品;李怡娜等[7]考虑了在需求依赖价格和提前期的市场中,面对时间敏感型和价格敏感型顾客时,企业如何根据顾客选择行为来确定最优的提前期和价格。本文研究与上述双渠道供应链定价决策问题密切相关,且本文还分析了顾客的策略型行为对最优定价的影响。关于双周期供应链,Maiti等[8]研究了批发价格在两个周期统一定价和区分定价两种情形下,制造商和零售商的定价策略;Haruvy等[9]研究了双周期定价策略,发现当生产成本较低时,制造商在第一周期开始公布第二周期价格的预先定价方案对制造商和消费者均有利;Li等[10]研究了制造商在第二周期存在学习效应,给出了制造商和零售商的反馈均衡解。此外,部分学者同时考虑了双渠道和双周期问题。Huang等[11]研究了需求中断的双周期双渠道模型,发现在需求中断下,无论是集中还是分散决策,最优生产数量都具有稳健性;Yu等[12]针对耐用品考虑双周期双渠道模型,设定制造商在直销渠道销售耐用品的同时向零售商销售和出租耐用品,认为零售商在第二周期会退出市场。然而,上述研究双周期双渠道的文献并未充分考虑策略型顾客,尤其是对第二周期低价的策略性顾客等待行为未作研究。
从顾客角度来讲,有些顾客对价格要素比较敏感,耐心型顾客往往愿意等到换季或打折时才购买产品。此外,顾客对直销渠道和零售商渠道的购买意愿也不相同。在理论方面,也有学者以策略型顾客为视角对双渠道供应链管理进行了研究。Chiang等[13]最早研究了面对策略型顾客的双渠道供应链,发现零售商并不总是受到威胁;Xu等[14]研究了顾客对直销渠道的认可度和交货提前期关于双渠道供应链定价的影响。另外,一些学者将顾客对产品估值限仅定为高估值和低估值两种情形[15],而本文对产品估值的设定是不确定的,更符合现实情形。类似地,在双周期定价模型中考虑策略型顾客亦有研究。杨慧等[16]研究了消费者在行为规则上表现出策略型或短视型的不同特征且估价呈随机分布的市场环境下产品的二周期动态定价决策问题;Lin等[17]考虑顾客耐心程度,研究了单渠道双周期定价问题。关于考虑策略型顾客的双周期文献只研究了单一零售商和顾客组成的二级供应链的定价策略[15-16,18],而本文研究了由“制造商—零售商—顾客”构成的三级供应链,并分析了顾客的策略行为对制造商和零售商的影响。
基于上述文献分析,目前国内外学者对双渠道供应链、双周期供应链和顾客策略行为问题已取得了丰硕的成果,为本文的研究奠定了很好的研究基础。但值得注意的是,现有文献对上述3个问题的研究是相互独立或者两两相互独立的,对于顾客策略行为下考虑双周期双渠道的供应链决策研究略显不足。鉴于此,本文以策略型顾客为视角,基于双周期双渠道策略型顾客的效用函数,考虑顾客耐心程度,对直销渠道认可度以及送货提前期这3个参数,构建双周期双渠道供应链的需求模型,给出制造商和零售商的定价决策,并采用数值分析方法,分析了体现顾客行为的3个参数对制造商和零售商利润的影响,研究了单周期和双周期两种情形下制造商和零售商利润的大小关系,探讨了顾客策略行为的作用与价值,以期得到有意义的管理启示。
1 基本模型
1.1 制造商和零售商
考虑由一个制造商和一个零售商组成的双周期双渠道供应链系统。在第一周期,制造商向零售商销售产品,同时也通过直销渠道直接向消费者销售产品。例如,当产品刚上市时,李宁、华为等通过线下零售和直销渠道销售。在第二周期,只有制造商在直销渠道销售产品。例如,多家品牌商在唯品会等平台或参与双十一等活动促销或清仓。假设制造商与零售商的决策过程服从Stackelberg博弈,其中制造商为Stackelberg博弈的主导者,则其决策顺序为:首先制造商给出第一周期的批发价格w和直销价格pd1(4)当顾客选择在直销渠道购买时,会事先被告知产品的提前期,而对提前期这一承诺的实现是建立顾客对直销渠道信任的关键,这也是多家在线平台比如天猫,京东,唯品会等关于提前期竞争的原因。因此,和文献[19]一样,本文将提前期作为非决策变量。;然后零售商作为跟随者确定第一周期的零售价格pr1;最后制造商确定第二周期直销渠道的销售价格p2。
为简化模型,假设所有产品的生产成本为0。通常地,制造商通过零售渠道的单位销售成本高于直销渠道成本,这里销售成本指产品运输成本和储存成本(5)在高科技电子产品、时尚品等行业,制造商为零售商运输产品为待售成品,而直销渠道销售往往采取按订单组装的策略,因此除在零售渠道产生运输成本外,还会有比直销渠道较高的储蓄成本。,和文献[20]一样,假设直销渠道的销售成本为0,而零售渠道的销售成本为cr>0。除此之外,在直销渠道还会产生单位交货成本m/t,这里m>0为交货总成本,t为订货提前期[14],且满足cr>m/t,即零售渠道的单位成本大于物流成本。若不满足该条件,制造商将只采用零售渠道来销售产品。
1.2 策略型顾客
用3个维度的差异来刻画顾客的异质性:①面对零售渠道和直销渠道,消费者的支付意愿不同。消费者在零售渠道购买产品的支付愿意为v,由于通过直销渠道购买无法触摸商品,在网络渠道购买产品的支付意愿为θv,其中θ为消费者对直销渠道的认可度[13],0<θ<1;②顾客去零售店可立即拿到产品,但在网上购买需要等待一定的时间,即存在订货提前期为t,t>0;③选择等到第2个销售周期购买的顾客,其耐心程度也不同,用参数0<ρ<1来表示顾客的耐心程度(6)文献[21-22]将ρ定义为贴现因子,鉴于本文侧重于研究顾客的策略性行为,和文献[18]一样,将其定义为顾客耐心因子,事实上,张维迎的《博弈论与信息经济学》中将贴现因子解释为参与人的耐心程度,取值越大说明参与人的耐心越好[23]。,当ρ逼近于0时,顾客为短视型顾客,当ρ逼近于1时,顾客为无限耐心型[18]。因此,消费者在双周期双渠道供应链中对应的效用函数分别为:
(1)第一周期零售渠道的顾客效用函数为ur1=v-pr1;
(2)第一周期直销渠道的顾客效用函数为ud1=θv-pd1-φt;
(3)第二周期直销渠道的顾客效用函数为u2=ρ(θv-p2-φt)。

1.3 需求函数
基于对策略型顾客效用函数的分析,本节旨在建立双周期双渠道供应链的需求模型。
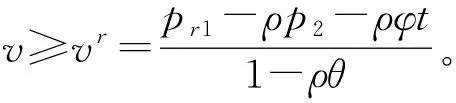
相反,如果估值未超过vdr,则会选择第一周期在线购买方式。通过计算可得到,当vd≤vr时,vd,vr,vdr满足vd≤vr 其次,根据vr和vd的大小关系分析顾客在各个小区间段上的行为。当vd≤vr时,顾客估值满足v2≤vd1≤vd≤vr≤vdr,vr1≤vr。如图1所示,根据比较顾客效用u发现,当估值v落在区间[v2,vd],顾客倾向于在第二周期购买,估值位于区间[vd,vdr]的顾客倾向于在第一周期直销渠道购买,而估值在区间[vdr,1]的顾客倾向于在第一周期从零售商购买;而当vr 最后,通过顾客估值v的分布给出双周期双渠道的需求函数。将消费者总人数单位化为1,每位顾客至多只能购买一件产品,且假设顾客估值v为在区间[0,1]的均匀分布,用Qr1和Qd1分别表示第一周期零售渠道和直接渠道的市场需求,Q2为第二周期的市场需求。因此,双周期的需求函数可以由如下分段函数给出: (1) 等价地,当(1-ρ)θpr1≥(1-ρθ)pd1-ρ(1-θ)p2+(1-ρ)φt时, (2) 当(1-ρ)θpr1<(1-ρθ)pd1-ρ(1-θ)p2+(1-ρ)φt时, Qd1=0, (3) 因此,借助消费者效用函数,考虑战略型消费者的双周期双渠道供应链的需求模型由分段线性函数式(2)和式(3)给出。式(2)和式(3)反映了自身价格、渠道间交叉价格以及周期间交叉价格对需求函数的影响。 本章分析双周期双渠道供应链的最优定价。假设制造商为Stackelberg主导者,零售商为追随者,其决策顺利如1.1节所述。下面采用逆向求解法给出制造商和零售商的最优决策。 在第二周期,制造商只通过直销渠道来销售产品。给定第一周期制造商批发价格,直销价格和零售商售价,制造商根据市场需求制定最优的价格p2最大化其第二周期利润πm2, πm2=(p2-m/t)×Q2。 (4) 式中p2和Q2的关系如式(2)和式(3)所示。 对于给定第一周期的售价pd1和pr1,策略型顾客将比较不同周期下对应渠道的顾客效用,可分为如下3个区域: R1={(pd1,pr1)|2θ(1-ρ)pr1+ρ(1-θ)m/t≥ (2-ρ-ρθ)pd1+2(1-ρ)φt}, R2={(pd1,pr1)|θ(2-ρ-ρθ)pr1<2(1-ρθ) pd1+(2-ρ-ρθ)φt-ρ(1-θ)m/t}, 相应地,制造商根据策略型顾客的不同反应给出第二周期的定价。 命题1给定第一周期制造商和零售商的售价后,第二周期制造商最优的定价为 (5) 2θ(1-ρ)pr1+ρ(1-θ)m/t≥(2-ρ-ρθ)pd1+ 2(1-ρ)φt。 R1={(pd1,pr1)|2θ(1-ρ)pr1+ ρ(1-θ)m/t≥(2-ρ-ρθ)pd1+2(1-ρ)φt}。 R2={(pd1,pr1)|θ(2-ρ-ρθ)pr1<2(1-ρθ) pd1+(2-ρ-ρθ)φt-ρ(1-θ)m/t}。 证毕。 当给定制造商的批发价格w和直销价格pd1时,零售商的利润可表示为 πr=(pr1-w)Qr1, (6) 其中, Qr1= (7) 首先,考虑(pd1,pr1)的情况,容易验证式(6)中的目标函数是关于零售价格pr1的凹函数。因此,存在唯一的最优解 (8) 将其带入区域R1中的限制条件可得w≥l1,其中 其次,当(pd1,pr1)时,可通过最大化(pr1-w)Qr1得到最优售价为 w+ρφt+ρm/t], (9) 将其带入区域R2中的约束条件中可得w 为了表述方便,按如上方式定义li,i=1,2,3,则这3条直线将由批发价格w和直销价格pd1构成的二维平面{(pd1,w)|w≤pd1}划分为4个区域(如图2)。 r1={(pd1,w)|l1≤w≤pd1}, r2={(pd1,w)|l3≤w r3={(pd1,w)|0≤w r4={(pd1,w)|l2≤w 通过上述分析可知,(pd1,w)落在r1或r2时,pr1取值均为式(8)。当(pd1,w)落在r3上时,pr1取值为式(9)。当(pd1,w)落在r4上时,pr1的取值在区域R2和区域R3相交的直线上取得,即pr1满足 θ(2-ρ-ρθ)pr1=2(1-ρθ)pd1+(2-ρ-ρθ) φt-ρ(1-θ)m/t。 证毕。 下面给出零售商的最优定价策略。 命题2对于给定的制造商批发价格w和直销价格pd1,零售商的最优定价: (10) 命题2表明在区域r1或r2,批发价格w和直销价格pd1都较低,大部分消费者倾向于在第一周期购买,其售价和顾客耐心不相关;而在区域r3,批发价格w和直销价格pd1都较高,顾客呈现观望状态,为了吸引顾客在零售商购买,零售价格的设定随着耐心程度的增大而减少。 本节主要确定第一周期的最优批发价格w和直销价格pd1来最大化制造商的总利润,而制造商的总利润函数πm1为(7)这里对第二周期的利润乘以ρ,主要是因为制造商第二周期利润的贴现是由于顾客的耐心导致的,即(11)中制造商利润函数是以第一周期为时间点的,顾客有耐心等到第二周期购买,使得制造商在第二周期的利润进行折现才能得出与第一周期同时间点的利润价值。文[23]也将贴现因子解释为参与人的耐心程度。 πm=(w-cr)Qr1+(pd1-m/t)Qd1+ ρ(p2-m/t)Q2。 (11) 式中:第一项为第一周期销售给零售商的利润,第二项为第一周期通过直销渠道获得的利润,第三项为第二周期直销渠道的利润。 如图2所示,需要在4个区域上分别求其决策。首先考虑区域r1和r2,对应决策由如下引理给出。 引理1在r1中,制造商最优定价在图2中的点a处取得;在r2中,制造商的最优定价在点b处取得。 证明在r1中,制造商的总利润如式(11)所示,其中: (2-ρ-θ)pd1+θ(1-ρ)w-(2-θ)(1-ρ) φt+ρ(1-θ)m/t], 因此,制造商的总利润为 [θ(1-ρ)(1-θ)- (2-ρ-θ)pd1+θ(1-ρ)w-(2-θ)(1-ρ) 等价于下式: 4θ(1-ρ)(1-θ)πm1=-2θ(1-ρ)w2- 2θ(1-ρ)(1-θ+cr+φt-m/t)w+2[θ(1-ρ) (1-θ)+(2-ρ-ρθ)m/t-θ(1-ρ)cr- (2-θ)(1-ρ)φt]pd1-2θ(1-ρ)(1-θ+φt)cr- 2θ(1-ρ)(1-θ)m/t+2(1-ρ)(2-θ)mφ- ρ(1-θ)m2/t2, 且满足 w≤pd1,(2-ρ-θ)pd1-θ(1-θ)(1-ρ)+ (1-ρ)(2-θ)φt-ρ(1-θ)m/t≤(1-ρ)θw。 该问题对应的Hessian矩阵为 H1= 矩阵H1的顺序主子式ΔH11、ΔH12满足: ΔH11=-2θ(1-ρ)<0, ΔH12=4θ(1-θ)(1-ρ)2+2θ(1-ρ) (1-θ)(2-ρ)>0。 因此,矩阵H1为负定的,由KKT(Karush-Kuhn-Tucker)条件可得: 4θ(1-ρ)pd1-4θ(1-ρ)w+2θ(1-ρ)(1-θ+ cr+φt-m/t)+λ1-θ(1-ρ)λ2=0, -2[2(1-ρ)+(2-ρ)(1-θ)]pd1+4θ(1-ρ)w+ 2[θ(1-ρ)(1-θ)+(2-ρ-ρθ)m/t-θ(1-ρ)cr -(1-ρ)(2-θ)φt]-λ1+(2-ρ-θ)λ2=0, λ1(-pd1+w)=0, λ2[(2-ρ-θ)pd1-(1-ρ)θw+(2-θ)(1-ρ) φt-ρ(1-θ)m/t-θ(1-θ)(1-ρ)]=0, 其中λ1,λ2≤0为朗格朗日乘子。经验证,只有当λ1<0,λ2<0时,存在最优解为: 即为图2中的点a值。 接下来,由式(5)和式(8)可得在第二周期对应区域r2的售价为: pd1-θ(1-ρ)w+(2-θ)(1-ρ)φt],Qd1=0, θw-(2-θ)φt], 在区域r2中,制造商的总利润为式(11),且 (2-θ-ρθ)pd1-θ(1-ρ)w+(2-θ)(1-ρ) φt-2ρ(1-θ)m/t][θ(1-θ)-(2-θ)pd1+ θw-(2-θ)φt], 等价于: θ[2ρ(1-θ)+θ(1-ρ)]w2+2θ(2-θ-ρθ)wpd1+ [2θ(1-ρ)(ρ-θ)+2ρθ(1-θ)cr+2θ(2-θ-ρθ) φt-2ρθ(1-θ)m/t]w+[2θ(1-θ)(2-ρ-θ)- 2(2-θ)(2-ρ-θ)φt-2ρθ(1-θ)cr+2ρ(1-θ) (2-θ)m/t]pd1-2ρθ(1-θ)(1-θ+φt)cr+ [θ(1-θ)-(2-θ)φt][-θ(1-ρ)(1-θ)+ (2-θ)(1-ρ)φt-2ρ(1-θ)m/t]。 且满足: w≤pd1, (12) (4-3ρθ-2θ+ρθ2)pd1+(2-θ)(2-ρ-ρθ) φt-2ρ(1-θ)m/t-θ(1-θ)(2-ρ-ρθ)≤θ (2-ρ-ρθ)w, (13) θ(1-ρ)w<(2-ρ-θ)pd1-θ(1-θ)(1-ρ)+ (1-ρ)(2-θ)φt-ρ(1-θ)m/t。 (14) 该问题对应的Hessian矩阵为 矩阵H2的顺序主子式ΔH21,ΔH22满足: ΔH21=-(2-θ)(2-θ-ρθ)<0, ΔH22=4ρθ(2-θ-ρθ)(1-θ)2>0。 因此,矩阵H2为负定的。而在直线w=pd1上, (2-ρ-θ)φt+ρ(1-θ)m/t]。 考虑4ρθ(1-θ)2Πm2在约束条件(12)和(13)下的最优问题,由KKT条件可得: -2(2-θ)(2-θ-ρθ)pd1+2θ(2-θ-ρθ)w+ 2θ(1-θ)(2-ρ-θ)-2(2-θ)(2-ρ-θ)φt -2ρθ(1-θ)cr+2ρ(1-θ)(2-θ)m/t-λ1+ (4-3ρθ-2θ+ρθ2)λ2=0, -2θ[2ρ(1-θ)+θ(1-ρ)]w+2θ(2-θ-ρθ) pd1+2θ(1-θ)(ρ-θ)+2ρθ(1-θ)cr+ 2θ(2-θ-ρ)φt-2ρθ(1-θ)m/t+λ1- θ(2-ρ-ρθ)λ2=0, λ1(-pd1+w)=0, λ2[(4-3ρθ-2θ+ρ2θ)pd1-θ(2-ρ-ρθ) w+(2-θ)(2-ρ-ρθ)φt -2ρ(1-θ)m/t-θ(1-θ)(2-ρ-ρθ)]=0。 其中λ1,λ2≤0为朗格朗日乘子。在以下两种情况存在最优解: 当λ1<0,λ2=0时存在最优解为 (15) 当λ1<0,λ2<0时存在最优解为 (16) 计算可得式(15)>式(16),而式(16)对应了r2中的点b,其值为r2中最大的值,因此式(15)对应的点不属于r2,舍去。证毕。 由图2可知,r1的批发价格和直销价格取值均较低,且第一周期直销渠道销售量在直线w=pd1上递减,并从原点0减少到a。而制造商第二周期的售价关于第一周期直销价格递增,且第二周期带来的边际利润高于第一周期在直销渠道的边际利润,因此制造商将最优决策设在点a。r2的性质和r1所对应的性质相似,也在其区域的最大值点取到最优解。事实上,对于制造商整体的最优决策并不在区域r1或r2中取得,而是在r3或r4取得,下面就给出在区域r3或r4的最优定价。 为方便起见,记: d=2-ρ-ρθ,e=(1-ρ)(3-2ρθ)+(1-ρθ)2, f=8-14ρ-8ρθ+5ρ2+13ρ2θ+2ρ2θ2- 3ρ3θ-3ρ3θ2, g=8-6ρ-8ρθ+ρ2+3ρ2θ+2ρ2θ2, h=4-4ρ-4ρθ+3ρ2θ+ρ2θ2, k=8-4ρ-10ρθ+3ρ2θ+3ρ2θ2, B=d(2d-2e-dρθ)(θdh-dhφt+ρkm/t)- (2-ρθ)2d2[θd2-d2φt-ρ2(1-θ)m/t]+ ρd(2-ρθ)[2(1-ρθ)d2(θ-φt)+(f-2de)m/t- g(1-ρθ)gm/t], C=d[θd2-d2φt-ρ2(1-θ)m/t](θdh-dhφt+ ρkm/t)+ρ[(1-ρθ)d2(θ-φt)+(f-2de)m/t] (θd2-d2φt+ρkm/t), D=θd2e2(2-ρθ)3(8-5ρθ)-(1-ρθ) (2-ρθ)(8-5ρθ)2B, E=-2θ(2-ρθ)(8-5ρθ)2d2e2[2(1-ρθ)+ρ (3-ρθ)(m/t+φt)]-(1-ρθ)(2-ρθ)(8-5ρθ)2B, F=2θd2e2[2(1-ρθ)(4-ρθ)+ρ2θ(m/t+φt)] [4(1-ρθ)2+ρ(4-3ρθ)(m/t+φt)]+ ρ(2-ρθ)d2e2[6θ(1-ρθ)-(8-7ρθ) (m/t+φt)]2-(1-ρθ)(2-ρθ)(8-5ρθ)2C。 对应地,第2周期售价为 并且,两周期的直销渠道销售量为 (2)如果参数满足情形2,则制造商的定价为: ρ2(1-θ)m/t], dcr-(1-ρθ)d2φt+fm/t]。 并且,制造商在直销渠道的销售量为 证明在r3和r4中,都有Qd1=0,第2周期的销售价和销售量为: 先研究区域r4,其制造商的总利润为 [θ(2-ρ-ρθ)-(2-ρθ)pd1-(2-ρ-ρθ) (17) 且满足w≤pd1,l2≤w (2-ρ-ρθ)cr-(2-ρ-ρθ)2φt-ρ2(1-θ)m/t] pd1-θ(2-ρ-ρθ)2cr+(2-ρ-ρθ)2crφt- ρ(2-ρ-ρθ)crm/t+ρ(1-ρθ)m2/t2, 对应的约束条件为: (2-ρθ)(4-2θ-3ρθ+ρ2θ)pd1+(4-3ρθ) (2-ρ-ρθ)φt-ρ(1-θ)(4-2θ-3ρθ+ ρ2θ)m/t-2θ(1-ρθ)(2-ρ-ρθ)≤0, -2(1-θ)(2-ρθ)pd1+2ρ(1-θ)m/t-(2-θ) (2-ρ-ρθ)φt+θ(1-θ)(2-ρ-ρθ)<0。 由KKT条件可得,在区域r4中的最优解为 (18) 在区域r3中,制造商的总利润为 [2θ(1-ρθ)+θ(2-ρθ)w-(4-3ρθ) (φt+m/t)]2。 (19) 且满足w≤pd1,w≤l2。这里制造商的利润函数并没有含有pd1,因此在区域r3中可以不考虑约束条件,只考虑利润式(19),可得 w=pd1= (20) 命题3表明,制造商对于定价策略的选择受参数ρ,θ,t,cr的影响。在双周期双渠道供应链中,制造商会根据参数是否满足门槛条件而采取对应的销售策略。尽管在第1周期设有直销渠道,但并没有产生销售量,制造商只是通过直销渠道来控制零售商的定价。但在第2周期,为满足耐心型消费者的需求,存在销售量。并由此结合引理1,可得到零售商最佳的零售价和销售量。 命题4(1)若在情形1下,则零售商的售价和销售量为: (2)若在情形2下,则零售商的售价和销售量为: (1-ρ)(2-ρθ)dφt-ρ(1-θ)lm/t)], ρ2θ2)φt+ρkm/t-(2-ρθ)2dcr]。 命题4给出了零售商面对制造商第1周期定价策略后的反应。通过零售商订购量表达式发现,如果制造商在零售渠道的销售成本过高,制造商选择在第一周期放弃零售渠道。特别地,如果顾客都是急性的,即耐心程度ρ=0,都在第一周期购买,则命题3和命题4中的条件和在第一周期中的结论与单周期双渠道模型[14]中的结果完全相同。 本节对制造商和零售商的利润进行数值分析,探讨顾客策略行为的作用与价值,重点研究顾客耐心程度,对直销渠道认可度及订货提前期的设定对制造商和零售商利润的影响,以期得到有意义的管理启示。 制造商通过在直销渠道设定清仓或促销的方式吸引追求低价且有耐心的顾客在第2个周期(促销周期)购买,但由于零售商只在第1周期中占有市场,制造商延长销售周期会对零售商构成威胁。本节将对比本文中的结论和现在的单周期双渠道模型的结论,探讨制造商设立促销周期对制造商和零售商的影响。下面先给出单周期双渠道供应链中的结论,该结论从文献[14]中直接得到。 在命题3和4中,当所有顾客为急性的,即ρ=0时,由于顾客在第2周期的效用函数为0,没有顾客会在第2周期购买产品。针对急性顾客市场对应的销售模式为单周期模式,并且其定价策略和引理2中一致。 本文研究了由开设直销渠道的单个制造商、单个零售商和策略型顾客组成的双渠道供应链系统,针对零售渠道和直销渠道冲突问题,结合现有厂家解决方案,研究了双周期双渠道模型的定价问题,主要得到如下结论: (1)提出了双周期双渠道供应链的需求函数,给出了每个周期对应渠道的销售量关于自身价格和交叉价格的影响。 (2)在本文提出的需求函数基础上,给出了面对策略型顾客,制造商和零售商的最优定价策略。 (3)通过数值实验,探讨了顾客耐心程度,直销渠道认可度和订货提前期对供应链成员利润的影响,并且比较分析了双周期和单周期供应链成员的利润,得到了如下研究结论和管理启示:①在第1周期开设直销渠道只是为了和零售商构成竞争,直销渠道并没有产生真正的销售量。②缩短提前期会提高制造商利润,但同时会使零售商利润降低,即缩短订货提前期会使渠道冲突更激烈。提高顾客对直销渠道认可度,会提高制造商利润但会使零售商利益受损。③制造商开设第2周期线上清仓活动会使零售商的利润减少。这是由于随着顾客追求第2周期低价的耐心增强,制造商会趁机降低第1周期直销渠道价格与零售商争夺需求。而现实中,线下零售商往往会采用较好店内体验、售后等服务来和制造商竞争市场需求。④和单周期结论相比,制造商在双周期情形下的利润并不总是高于单周期情形下的利润。只有当顾客对直销渠道认可度小于某限定值时,制造商才会从开设第2周期中收益,这也是部分产品不参加“双十一”等在线促销活动的原因。 未来的研究可以从以下几方面进行扩展:和零售渠道即买即得的特点相比,本文考虑了直销渠道存在送货提前期的情形,但顾客在零售渠道购买会产生出行费用等,下一步研究将同时考虑提前期和出行费用两个因素,并重点研究渠道之间的服务竞争对定价的影响。另一方面,下一步可将订货提前期作为决策变量,甚至给出多种订货提前期和售价的组合,使研究更有实践意义。此外,本文的定价方法采用的是响应定价,因此也可考虑其他定价方法,如预先定价[18],并比较不同定价方法之间的优劣。最后,改变顾客估值的分布类型,在顾客估值异质化情形下,双周期双渠道供应链系统的定价决策也是值得进一步研究的方向。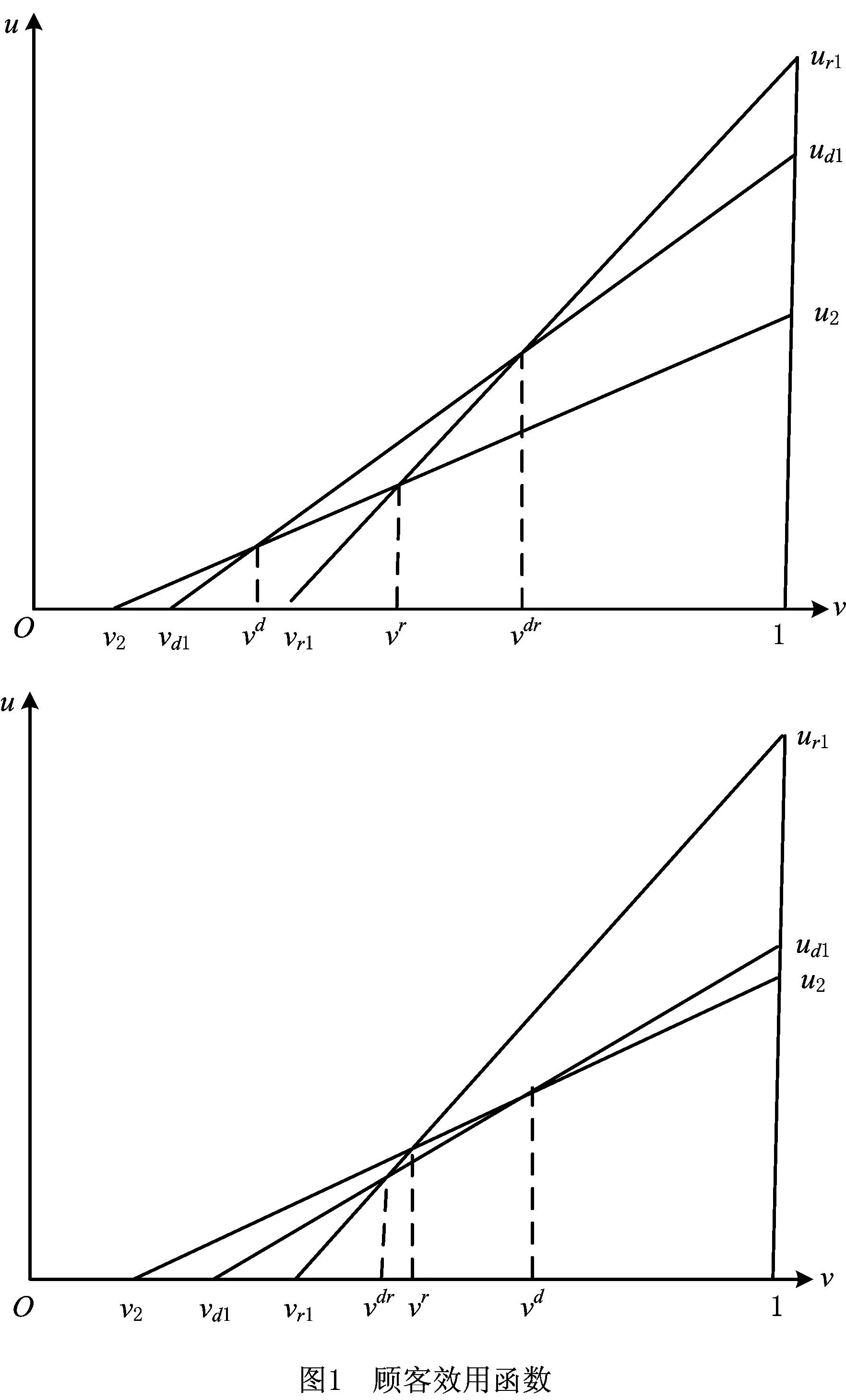
2 模型分析
2.1 第二周期直销渠道售价的确定
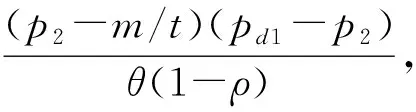


1.5 第一周期零售渠道售价的确定

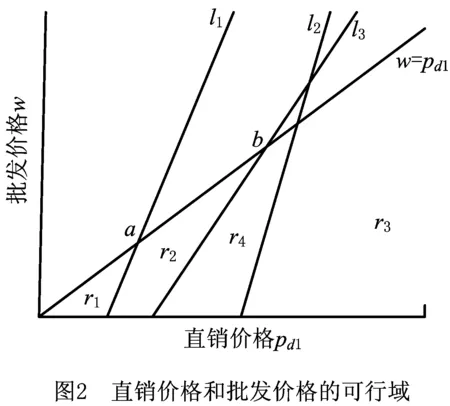
2.3 第一周期直销渠道售价和批发价的确定





3 数值分析
3.1 参数分析
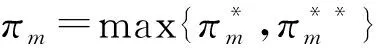
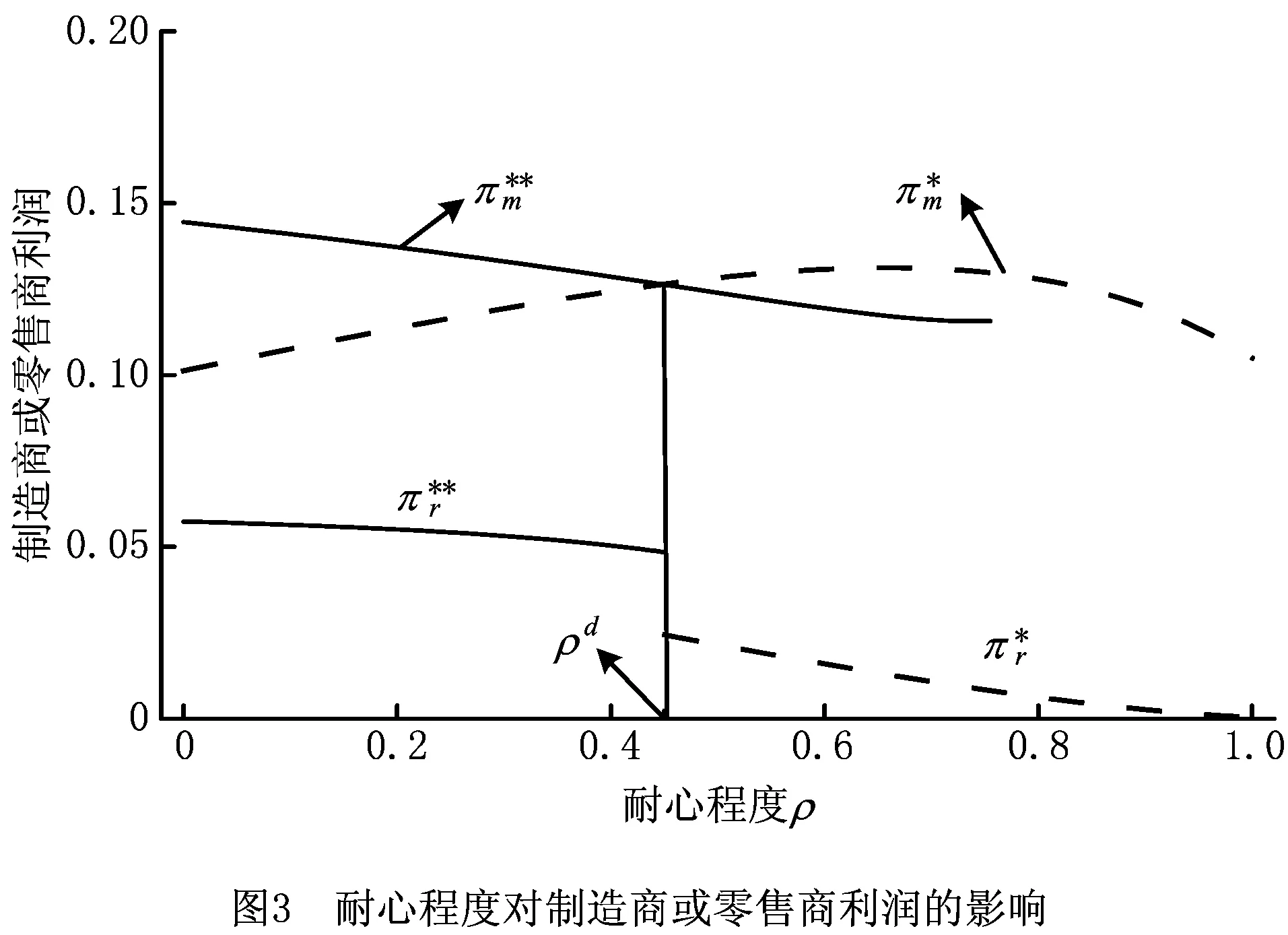

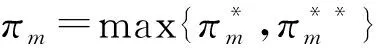
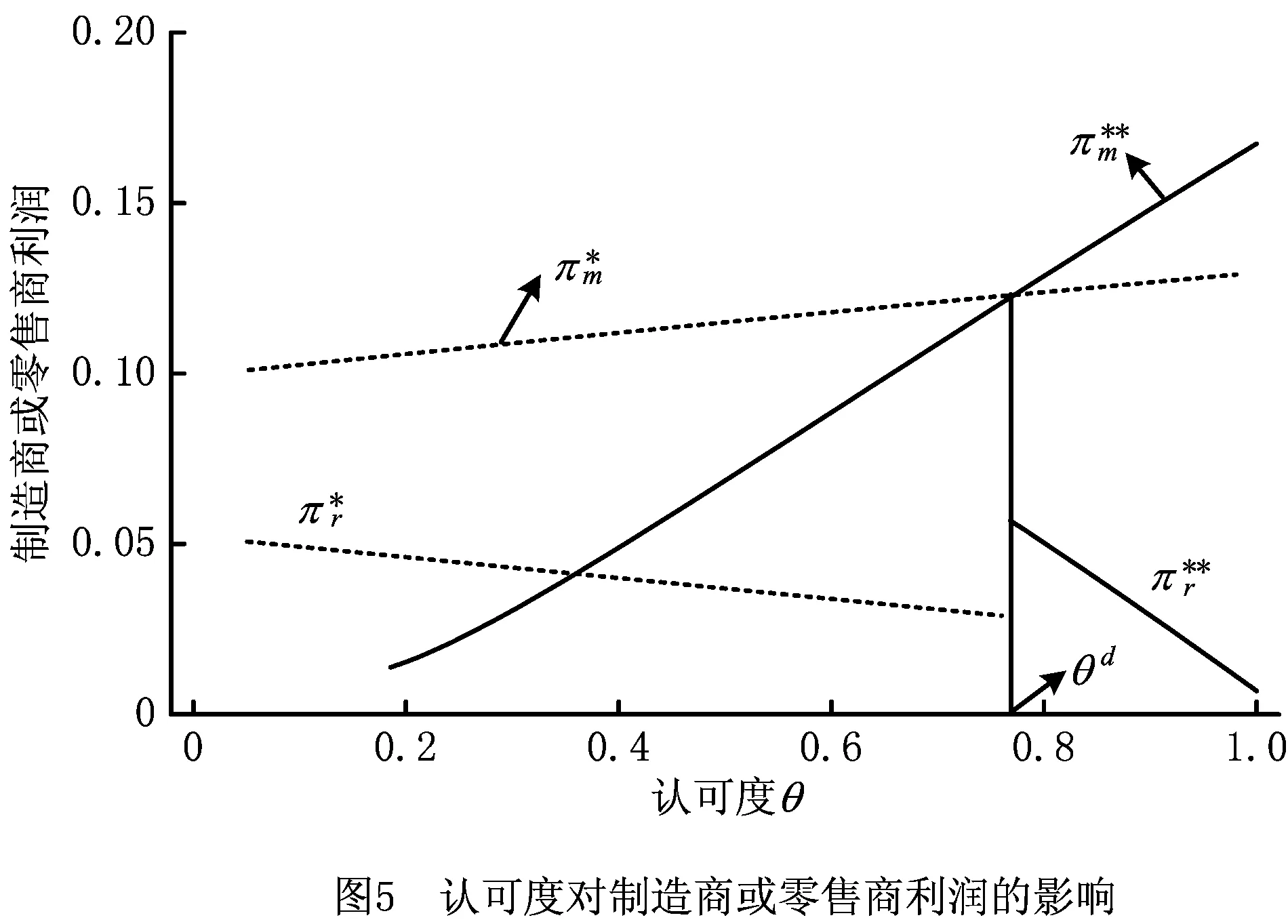
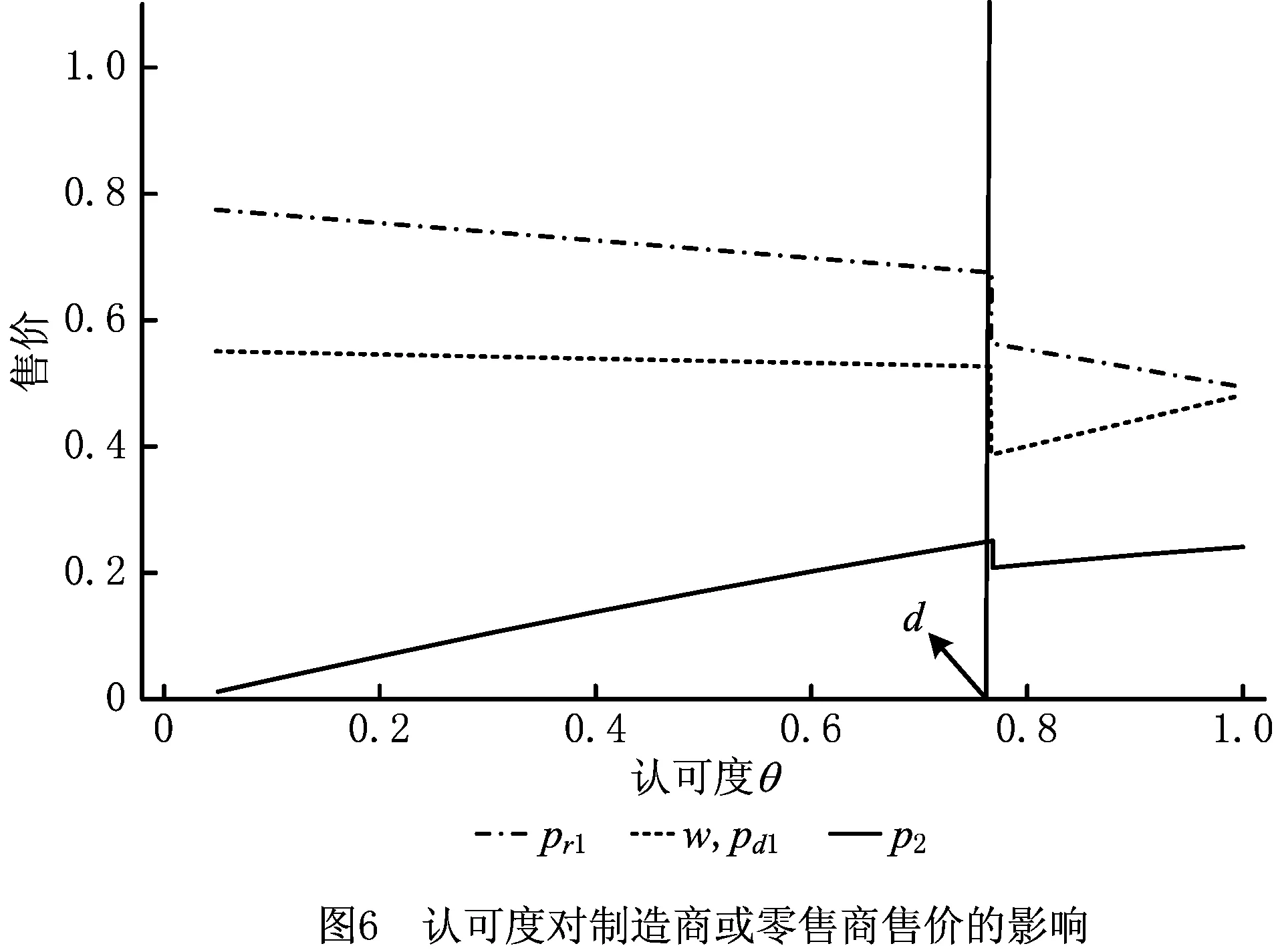
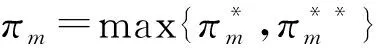


3.2 单周期和双周期的比较

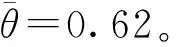
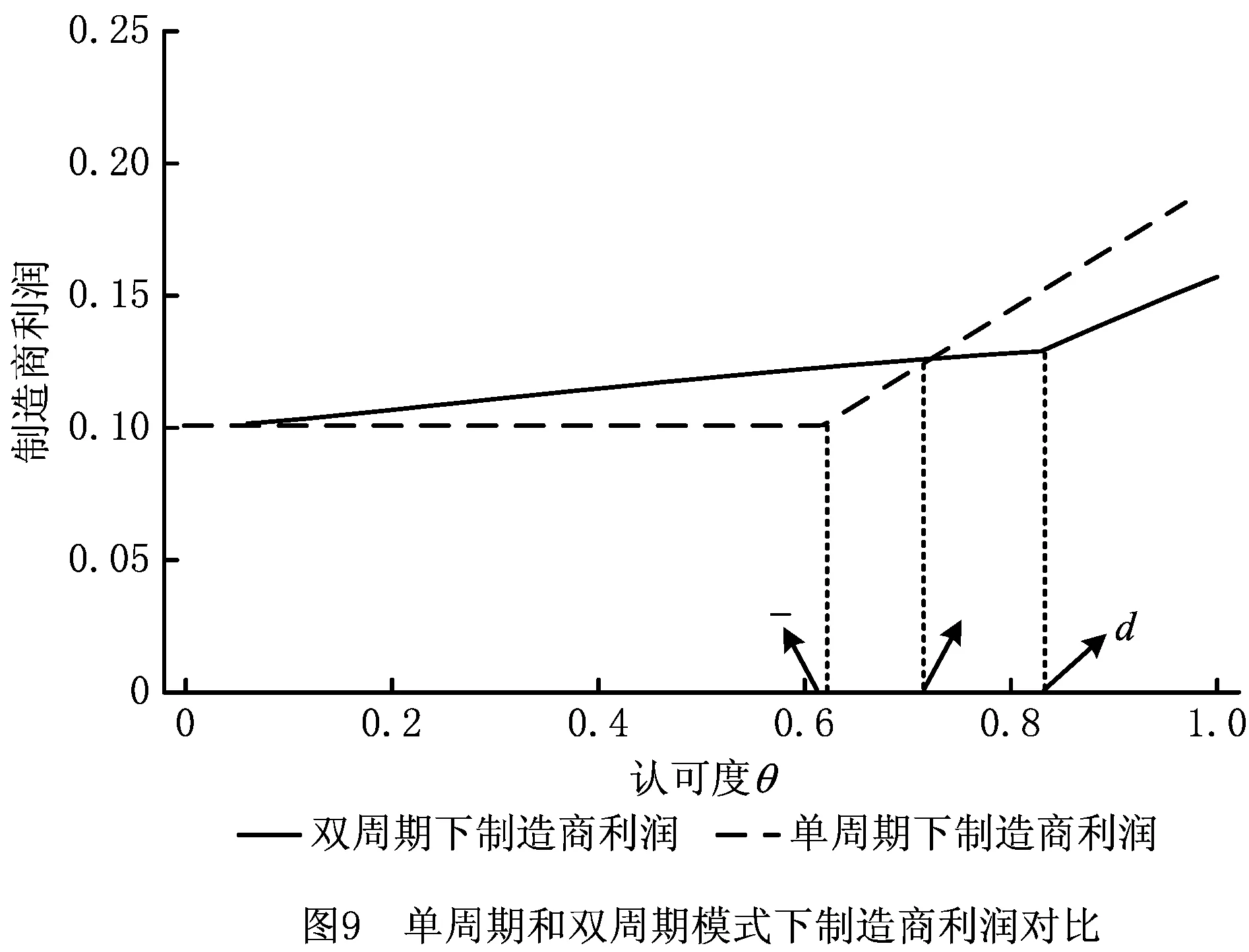


4 结束语
