可加势和次可加势水平集的2 个区别
2020-11-16马冠忠徐玲芳
马冠忠, 徐玲芳
(安阳师范学院数学与统计学院,河南安阳455000)
关于可加势水平集最早的研究是文献[1 -2],证明了对 α∈[0,1],水平集
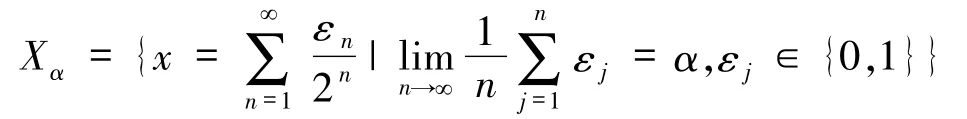
的Hausdorff维数为
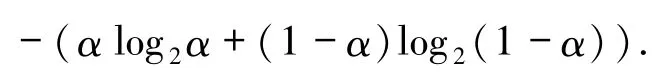
20 世纪80 年代以来,随着分形几何的迅猛发展和重分形理论的兴起,有关可加势水平集问题的研究呈现爆炸式增长.文献[3]为研究非共形变换的Lyapunov指数,首次提出了次可加势的概念并分析了次可加势的重分形;文献[4]把可加势的重分形分析推广到了一般的非可加势情形.国内外学者对各种水平集的分析性质、拓扑性质、热力学性质进行了深入的研究,得到了丰富的结果.目前,对非可加势的水平集的研究仍然是动力系统中维数理论和重分形领域的热点问题之一.但迄今为止,水平集的研究主要集中在考察水平集的分形维数、拓扑熵和拓扑压力以及相关的各种维数谱的连续性和正则性问题,见文献[1 -15].据我们所知,并没有文献系统地研究过水平集本身共有的性质,如水平集 Xα的不变性以及集合之间的包含关系等,其中水平集 Xα、集合的定义见第1 节.对可加势 Φ,可以证明 LΦ⊂ΩΦ(本文定理1),而且水平集Xα都是完全不变集(本文命题1).文献[9]提到了对拓扑混合有限型子位移中的可加势,有 LΦ=ΩΦ成立;文献[10]指出对共形斥子中的可加势,LΦ=ΩΦ也成立,但都没有给出证明.文献[11]证明了在拓扑混合有限型子位移中,对2 个可加势的商有 LΦ/Ψ⊂ΩΦ/Ψ成立;在文献[12]中,对饱和映射系统中的渐近可加势Ω,得到了LΦ=ΩΦ的结果.而本文例1 表明,存在动力系统和可加势,使得LΦ⊂ΩΦ但 LΦ≠ΩΦ.关于次可加势,文献[13]中的例1 表明,在拓扑混合有限型子位移中,有次可加势Φ使得LΦ⊂ΩΦ但LΦ≠ΩΦ.人们倾向于认为,对次可加势,仍然会有LΦ⊂ΩΦ成立,但并没有文献给出证明.在本文定理2 中证明了,对次可加势Φ,LΦ⊂ΩΦ未必成立.同时,在命题2 中证明了次可加势的水平集不再具有完全不变性.这些结果表明,次可加势的水平集和可加势的水平集有完全不同的性质,使人们对次可加势的水平集有了新的认识.
1 预备知识和主要结果
设(X,d)为紧度量空间,T:X→X 为连续映射,称(X,d,T)为拓扑动力系统.用 C(X)表示 X 上连续函数全体.用集合M(X)表示X 上概率测度全体,在M(X)中引入弱拓扑.本文中的测度均指正则 Borel概率测度.分别用 M(X,T)和 E(X,T)表示X上T-不变测度全体和T -不变的遍历测度全体.设为X上一列连续函数,对给定的x∈X,若极限存在,记
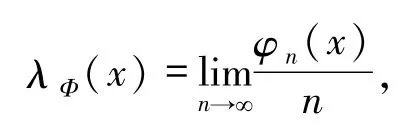
称λΦ(x)为Φ在x的Lyapunov指数.
若 Φ 满足:对一切 n≥1,m≥1,x∈X,都有
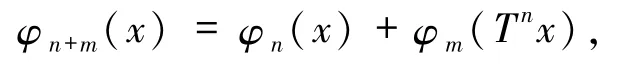
称Φ为可加势;若Φ满足:对一切n≥1,m≥1,x∈X,都有
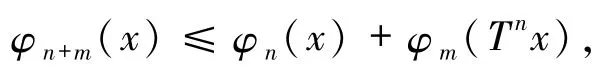
称Φ为次可加势.次可加势在动力系统的研究中占有非常重要的地位,动力系统中很多重要的特征量都可以表示为次可加势.如可微变换的Lyapunov指数(见文献[5,16 -18])和矩阵乘积的 Lyapunov指数等(见文献[6 -8]).
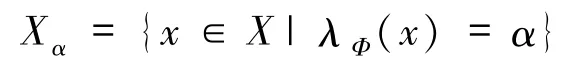
为Φ关于α的水平集.给定μ∈M(X,T),令
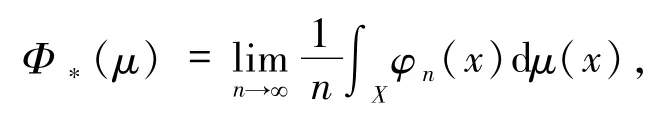
由次可加性知,上述极限存在.
沿用文献[9 -10,12]中记号,考虑下述 3 个集合:

设A为X的子集,若T(A)⊂A,称A 为正向不变集;若T-1(A)⊂A,则称A为反向不变集;若A既是正向不变集,又是反向不变集,则称A 为完全不变集.
本文主要讨论可加势和次可加势的集合LΦ、之间的包含关系以及水平集 Xα的不变性质,得到了下述主要结果.
定理 1设(X,d,T)为拓扑动力系统,Φ 为可加势,则有
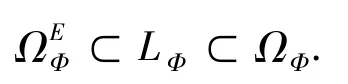
容易验证下述结论:
命题1设Φ为可加势,水平集Xα≠Ø,则Xα是完全不变集.
记单位闭区间[0,1]为 I,令 T(x)=4x -4x2,x∈I为 Logistic映射.设
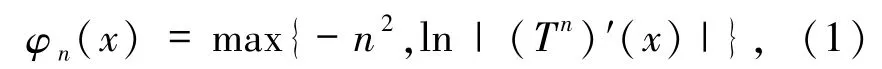
下面的定理2 和命题2 说明,对次可加势Φ如(1)式所定义,则有和定理1、命题1 及文献[13]完全不同的结论.
定理 2设 T(x)=4x-4x2,x∈I为 Logistic映射,次可加势如(1)式所定义,则对每个 μ∈M(I,T),都有 Φ*(μ)≥0.
记次可加势 Φ 关于 -∞的水平集为 I-∞,则I-∞={x∈I|存在 n≥0,使得为无限可数集.因此,-∞∈LΦ.但由定理2 知,-∞∉ΩΦ,故LΦ⊂ΩΦ不再成立.
下面命题表明,次可加势的水平集一般不再有完全不变性.
命题 2设 T(x)=4x-4x2,x∈I,次可加势 Φ如(1)式所定义,则水平集I-∞非正向不变集,水平集Iln4非反向不变集.
2 可加势的水平集
设Φ为可加势,则由M(X,T)在弱拓扑下的紧性知,ΩΦ为 R 中连通紧集.下面给出定理1 的证明.
定理1 的证明由 Birkhoff 遍历定理可知因而只需证 LΦ⊂ΩΦ.给定 x∈X,令VT(x)为概率测度序列的极限点集,由M(X)的紧性知,VT(x)非空.对给定的μ∈VT(x)和任意给定的f∈C(X),容易验证即 μ为 T -不变测度,则 VT(x)⊂M(X,T).任取α∈LΦ,即存在 x∈X,使得对每个μ∈VT(x),易证 Φ*(μ)=α,故 LΦ⊂ΩΦ.定理1 得证.
下面的例子表明,定理1 中的反向包含关系LΦ⊃ΩΦ不一定成立.
例1设
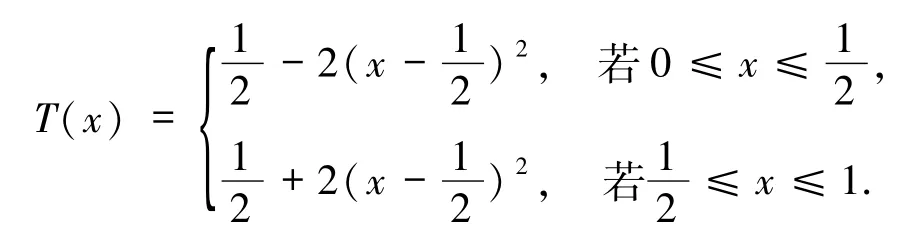
容易看出,映射 T:[0,1]→[0,1]的不动点集为{0,而且其中 δ 是质a量集中在点a 的Dirac 测度.由不变测度的遍历分解定理知,不变测度集合为
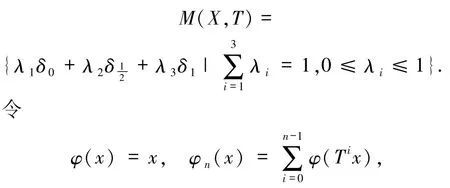
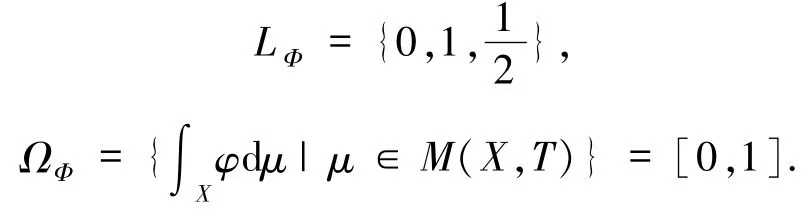
故 LΦ⊅ΩΦ.
注1在一些特殊的动力系统中,对可加势Φ,有LΦ=ΩΦ成立.例如,拓扑传递的有限型子位移[9]、共形斥子[10]、饱和映射系统[12]等.
注2到目前为止,不清楚对任意给定的可加势Φ,关系式是否总是成立.猜测上述包含关系不一定一般性的成立,即存在拓扑动力系统(X,d,T)和可加势 Φ,使得
3 次可加势的水平集
设 I为单位闭区间[0,1],称映射
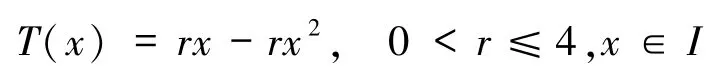
为Logistic映射.Logistic映射因生物学家May[19]在1976年发表的一篇论文而著名,后来应用在描述物种受到制约因素时的数量.当3.569 9≤r≤4 时,除少数特定的r值外,系统都会出现混沌现象.当r =4时,几乎所有初值都使Logistic系统出现混沌现象.此时,Logistic系统是2 个符号的全位移(Σ2,σ)的因子系统.
在证明定理2 和命题2 之前,先来介绍ΩΦ的一些性质.由Kingman次可加遍历定理可知:
命题3设Φ为次可加势,则有
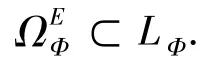
注3这是次可加势保留可加势的唯一一个性质.
命题 4设 Φ 为次可加势,则有 ΩΦ= (α,β],其中
命题4 可由下述2 个引理得到.回顾第1 节中Φ*(μ)的定义,则有:
引理1设Φ 为次可加势,则映射Φ*(μ)在M(X,T)上半连续.
证明对任意给定的测度序列依弱拓扑收敛到μ,只需证
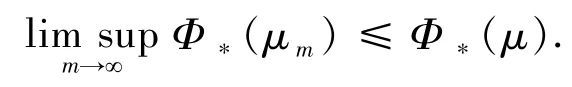
固定m,由次可加性,对一切n≥1,有下式成立
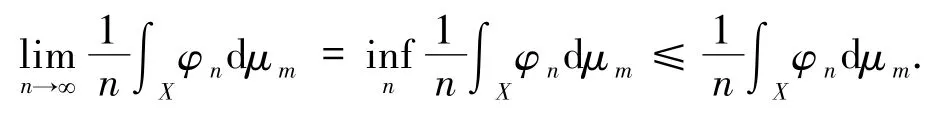
在上式中对m取上极限,则对一切n≥1,有
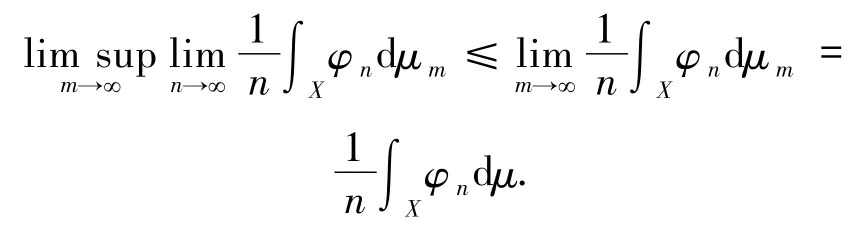
在上式中再令n→∞,即得结论.
注4可以证明,在下述2 个附加条件下,Φ*(μ)是 M(X,T)上的连续函数.
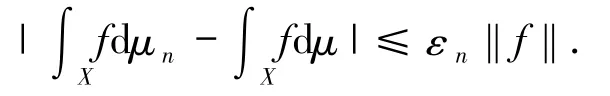
因本文并不需要这个结论,故略去证明.
引理2设Φ 是次可加势,ΩΦ如第1 节中所定义,则ΩΦ是中凸集.
三人站在崖顶,向下望,但见陡直的岩壁直直切下,深不见底。崖间云雾翻腾,偶有岩鹰壮硕的翅膀从云中穿过,发出一声尖利的鸣叫,回音久久在山间传响。
证明对任意给定的T -不变测度μ 和ν,实数0≤λ≤1,只需要证明
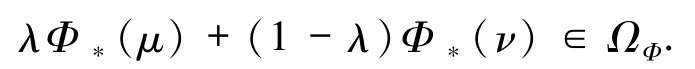
注意到
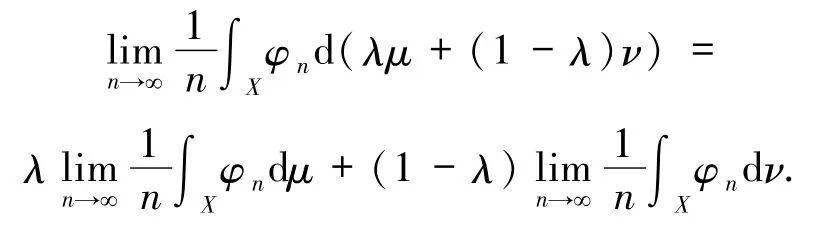
再由 M(X,T)的凸性,即得
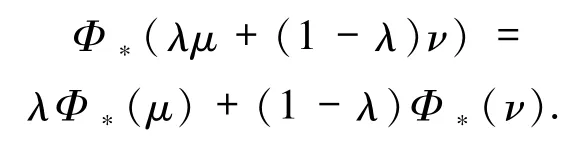
结论得证.
由引理1 和引理2,并注意到M(X,T)的紧性,命题4 得证.
在定理 2 的证明中,Przytycki[18]中的定理 B 起着关键的作用,为此先回顾一维实动力系统的几个概念,读者可以参看文献[20]中的第二章和第四章内容.设I为紧区间,T:I→I为实连续映射.
(b)非平坦临界点.设T:I→I 为实可微映射,若 T′(c)=0,称点 c为 T的临界点.进一步,设 T有二阶连续导数,若存在α≥2,使得
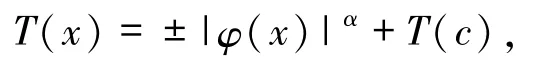
其中φ为局部C2(即2 阶导数连续)微分同胚且φ(c)=0,则称点c为T的非平坦临界点.
(c)T的吸引周期轨的吸引域B(T).设点p为周期点,O(p)为点p的周期轨道,称集合
B(O(p))= {x∈I|Tn(x)→O(p),n→∞}
为周期轨 O(p)的吸引邻域.若 B(O(p))包含非退化区间,称O(p)为吸引周期轨. B(T)为 T 的所有吸引周期轨的吸引邻域的并集.
(d)游荡区间.称子区间J⊂I 是T 的游荡区间,若{Tn(J)|n≥0}两两不交且子区间 J 的 ω 极限集ω(J)不是周期轨.
定理 A[18]设 T:I→I是光滑映射,且 T 仅有有限个非平坦的临界点,测度μ为Julia 集J(T)上任一T-不变测度,则对μ和a.e.x∈J(T),有
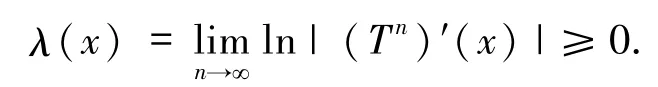
引理 3[20]设 T:I→I 为实映射,则 Julia 集J(T)是周期吸引轨的吸引域和游荡区间的余集.
引理 4[20]设 T:I→I为 C2实映射,且T仅有非平坦临界点,则T无游荡区间.
定理2 是文献[18]中的定理B 和下述命题5的直接推论.
命题 5设 T(x)=4x-4x2,x∈I为 Logistic映射,则 Julia集 J(T)=I.
证明由文献[20]中的第4 章引理和第6 章定理6.2 可以立即推出命题5.首先,注意到Logistic映射T 唯一的临界点为非平坦临界点,由引理4 可知,映射T:I→I无游荡区间.同时,注意到该系统是2个符号的全符号空间(Σ2,σ)的因子,而全符号空间中具有任意正整数周期的周期点稠密,因此,对每个点x∈I,点x的任一邻域中都有任意正整数周期的周期点存在,故该系统的吸引周期轨的吸引域B(T)是空集.由引理 3 知,J(T)=I.命题 5得证.
定理2 的证明由命题5 知
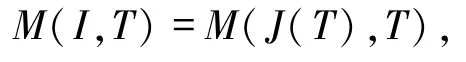
故对每个 μ∈M(I,T),由 Fatou 引理和文献[18]中的定理B可得
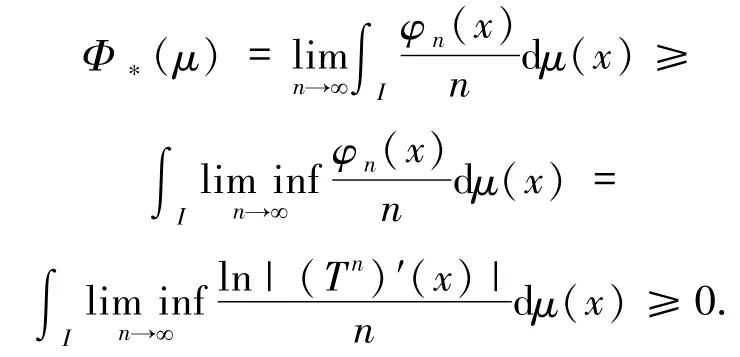
定理2 得证.
致谢安阳师院大学生创新基金(ASCX/2019-Z107)对本文给予了资助,谨致谢意.
